Lua 面向对象编程
Lua 面向对象编程
Lua 是一种轻量级的编程语言,通常用于嵌入应用程序中,提供灵活的扩展和定制功能。尽管 Lua 本身是一种过程式语言,但它提供了强大的元机制,允许开发者实现面向对象的编程范式。本文将探讨 Lua 中的面向对象编程(OOP)概念、实现方式以及最佳实践。
面向对象编程基础
面向对象编程是一种编程范式,它使用“对象”来设计软件。对象是数据和行为的封装单元。OOP 的核心概念包括:
- 类(Class):定义对象的蓝图,包括属性(数据字段)和方法(行为)。
- 对象(Object):类的实例,具有类定义的属性和方法。
- 封装(Encapsulation):隐藏对象的内部状态和实现细节,仅通过公共接口暴露功能。
- 继承(Inheritance):允许一个类继承另一个类的属性和方法。
- 多态(Polymorphism):允许不同类的对象对同一消息做出响应,表现出不同的行为。
Lua 中的面向对象
Lua 没有内置的类和对象系统,但它提供了表(table)和元表(metatable)等机制,允许模拟面向对象的行为。
表作为对象
在 Lua 中,表可以用来表示对象。表的字段存储对象的属性,而表的函数字段则表示对象的方法。
相关文章:

Lua 面向对象编程
Lua 面向对象编程 Lua 是一种轻量级的编程语言,通常用于嵌入应用程序中,提供灵活的扩展和定制功能。尽管 Lua 本身是一种过程式语言,但它提供了强大的元机制,允许开发者实现面向对象的编程范式。本文将探讨 Lua 中的面向对象编程(OOP)概念、实现方式以及最佳实践。 面向…...

AI赋能前端:你的Chrome 控制台需要AI(爱)
像会永生那样去学习,像明天就要死亡那样去生活。——圣雄甘地 大家好,我是柒八九。一个专注于前端开发技术/Rust及AI应用知识分享的Coder 此篇文章所涉及到的技术有 AI(Gemini)ChromeDevTool🪜魔法接码平台因为,行文字数所限,有些概念可能会一带而过亦或者提供对应的学习…...
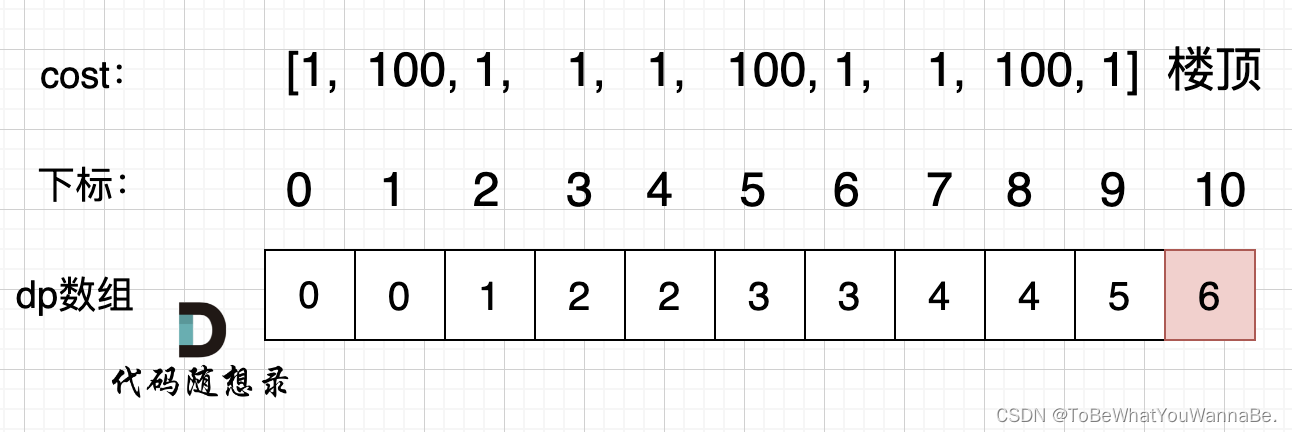
代码随想录-Day38
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 …...

CSS阴影优化气泡框样式
<body> <div class"pop">气泡框</div> </body>body{display: flex;justify-content: center;align-items: center;height: 100% } .pop{display: flex;justify-content: center;align-items: center;background: #409eff;width: 150px;heigh…...

强化安全新篇章:韶关石油化工可燃气体报警器年检解析
韶关,这座位于广东省北部的城市,近年来在石油化工行业取得了显著的发展。 随着一批批大型石化企业的进驻和投产,韶关不仅成为了区域性的石化产业基地,也为地方经济带来了强劲的增长动力。 然而,随着石化产业的快速发…...

Centos7 Docker部署PgSQL
拉取镜像 docker pull postgres:14.7运行容器 docker run --restartalways --nethost --shm-size"2g" --name pgsql -v /home/postgresql/data/pgdata:/var/lib/postgresql/data -v /etc/localtime:/etc/localtime -e POSTGRES_PASSWORDtest2023 -d postgres:14…...

LeetCode:经典题之21、24 题解及延伸
系列目录 88.合并两个有序数组 52.螺旋数组 567.字符串的排列 643.子数组最大平均数 150.逆波兰表达式 61.旋转链表 160.相交链表 83.删除排序链表中的重复元素 389.找不同 1491.去掉最低工资和最高工资后的工资平均值 896.单调序列 206.反转链表 92.反转链表II 141.环形链表 …...

【C++11】initializer_list详解!
一、什么是initializer_list? nitializer_list 是一种C11新的类型特性,它允许我们以统一的方式初始化对象。它是一个代表数组的轻量级包装器,通常用于构造函数和函数参数中,以允许传递一个初始化元素列表。 initializer_list也是一种模板类…...

如何在Java中处理UnsupportedOperationException异常?
如何在Java中处理UnsupportedOperationException异常? 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在Java编程中,我们经常会遇到各…...
WPS没保存关闭了怎么恢复数据?4个方法(更新版)
想象一下,你正在用WPS奋笔疾书,灵感如泉水般涌出,突然间,电脑却跟你开了个玩笑——啪地一下,文档未保存就关闭了!是不是感觉像是被泼了一盆冷水,所有的热情瞬间熄灭?别急,…...
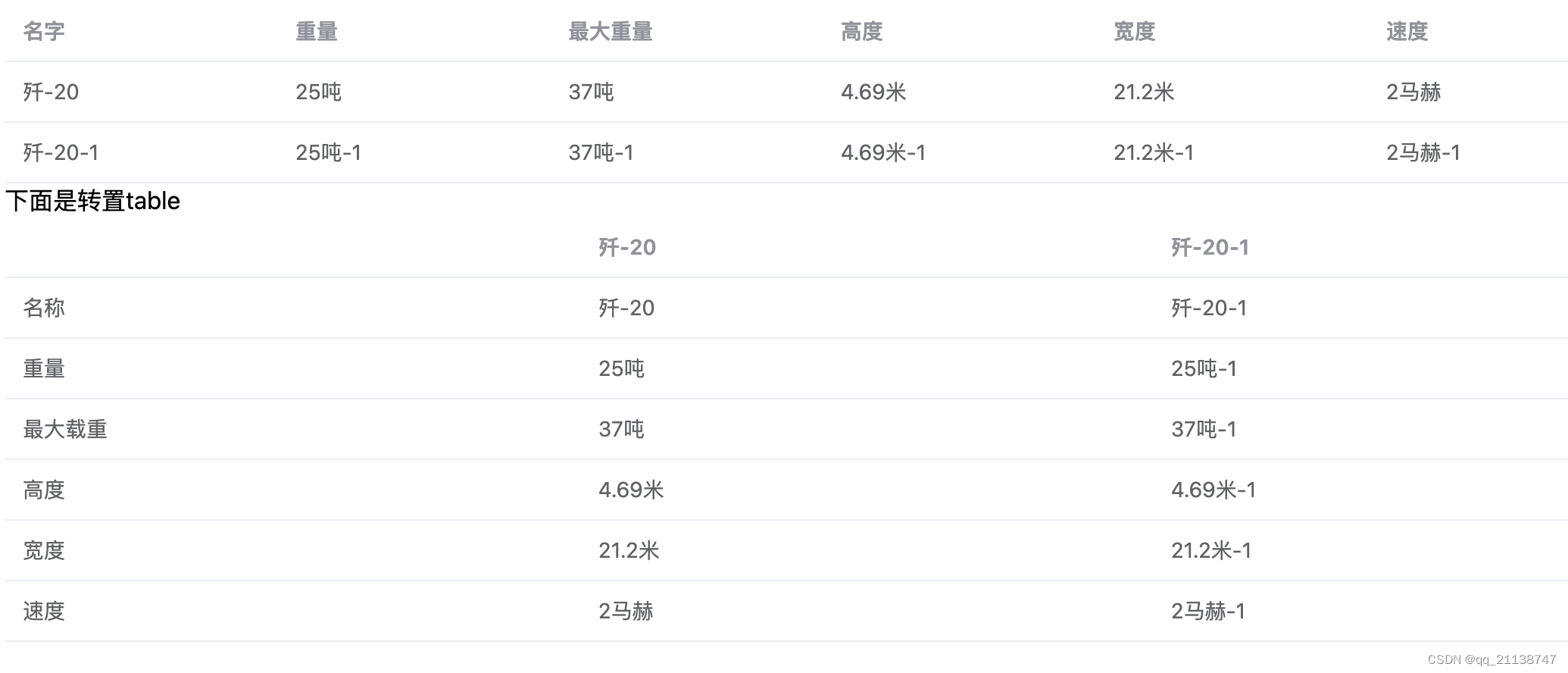
elementplus el-table(行列互换)转置
Element Plus v2.4.0, repl v3.4.0 <template> <div><el-table :data"tableData" style"width: 100%"><el-table-column prop"name" label"名字" width"180" /><el-table-column prop"wei…...
Gradle 核心之 Task
一、前言 只有 Task 才可以在 Gradle 的执行阶段去执行(其实质是执行的 Task 中的一系列 Action),所以 Task 的重要性不言而喻。 二、Task 2.1 Task 定义与配置 Task 的定义方式有如下两种: Task 的配置方式也有如下两种…...
【React 】折叠面板,点击展开时再请求数据
需求背景:使用折叠面板的形式展示数据,面板内部数据需要在打开时请求接口获取。 遇到问题:最开始使用Antd 的折叠面板组件,它对于数据直接渲染是没问题的,但是不好满足打开面板时再动态加载数据的需求,于是…...

c++学习 文件操作,模板
文件操作 #include<iostream> #include<string> #include<fstream> using namespace std; //文本操作 //程序运行时产生的数据都属于临时数据,程序一旦运行结束都会被释放 //通过文件可以数据持久化 //c中对文件操作包含头文件<fstream> /…...
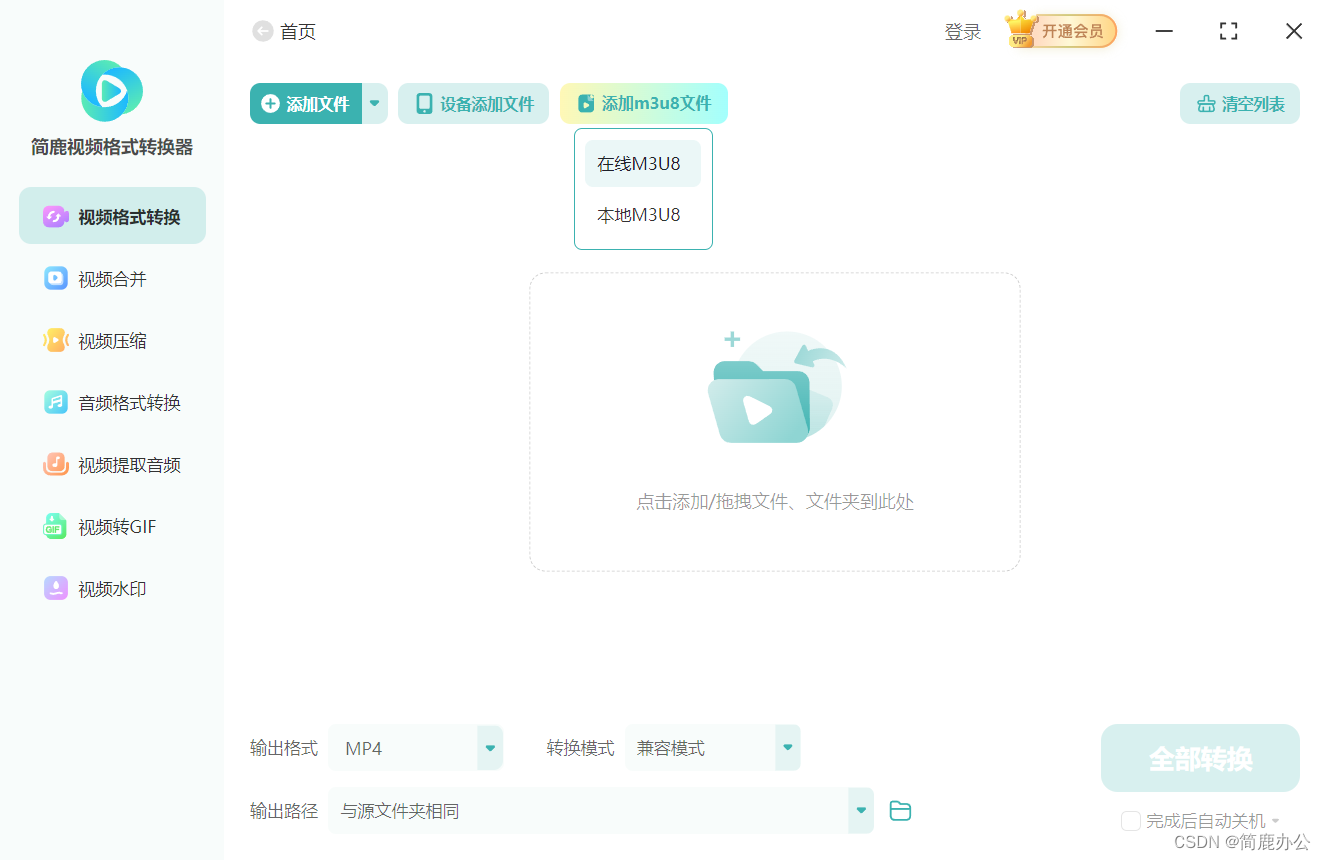
开源与在线 M3U8 Downloader 项目介绍及使用指南
M3U8 是一种用于播放列表格式的文件类型,广泛应用于流媒体服务中,特别是 HLS(HTTP Live Streaming)协议。它包含了一系列的 TS(Transport Stream)视频片段地址,使得视频能够分段加载,…...

正则表达式与文本处理器
正则表达式 基础正大表达式 查看特定字符 grep grep-n the test.txt grep-in the test.txt-n 显示行号 -i 不区分大小写 -v 反转查找 [] :中括号里可以写元素,内容符合任意元素,就会过滤出来 ^ :写在中括号里,代表取反。以^开头&…...

RedisTemplate方法一览表
数据类型RedisTemplate 方法Redis命令解释应用场景stringopsForValue().set(key, value)SET设置存储在指定 key 下的值存储简单数据,如用户的设置、配置项opsForValue().get(key)GET获取存储在指定 key 下的值读取存储的数据,如用户信息、配置参数opsFor…...

个人对devops的一点见解
DevOps 是一种将开发(Development)和运维(Operations)相结合的理念和实践方法。 它强调打破开发团队和运维团队之间的传统壁垒,促进两个团队之间更紧密的协作和沟通,以实现更高效、更快速、更可靠的软件交付…...

HarmonyOS鸿蒙应用开发基础知识
参考 HarmonyOS鸿蒙应用开发 (二、应用程序包结构理解及Ability的跳转,与Android的对比)_hap(harmonyos ability package)包的开发-CSDN博客 HarmonyOS NEXT下一代编程语言仓颉介绍及入门-CSDN博客...
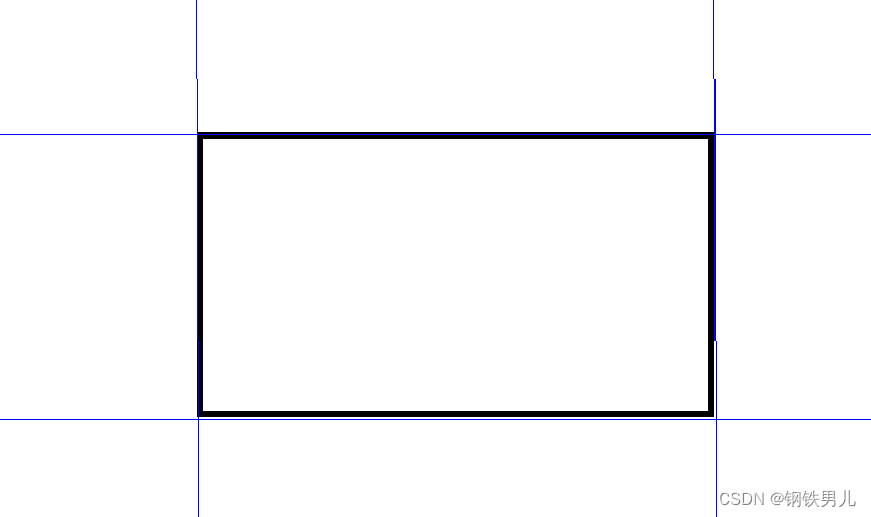
Halcon 根据霍夫变换在图像中寻找直线
一 霍夫变换 1 定义 霍夫变换是图像处理中从图像中识别几何形状的基本方法之一.几何形状包括圆,椭圆,直线等等. 2 直线方程 直线的方程可以用yk*xb 来表示,其中k和b是参数,分别是斜率和截距; 3 霍夫变换原理: 设…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
