逻辑回归(Logistic Regression)及其在机器学习中的应用
🚀时空传送门
- 🔍逻辑回归原理
- 📕Sigmoid函数
- 🎈逻辑回归模型
- 📕损失函数与优化
- 🎈损失函数
- 🚀优化算法
- 🔍逻辑回归的应用场景
- 🍀使用逻辑回归预测客户流失
- 使用scikit-learn库实现逻辑回归示例
- 🔍逻辑回归的优缺点
- 🚀逻辑回归优点
- 📕逻辑回归缺点
- 🎈逻辑回归缺点的优化方法
逻辑回归是一种广泛应用于机器学习和数据分析领域的分类算法,特别适用于二分类问题。尽管名字中包含“回归”,但逻辑回归实际上是一种分类方法,它通过对数据进行线性回归分析,并使用一个逻辑函数(通常是Sigmoid函数)将线性回归的连续输出转换为二分类问题所需的概率值。
🔍逻辑回归原理
📕Sigmoid函数
Sigmoid函数,也称为逻辑函数,是一个将任意实数映射到[0, 1]区间的函数。在逻辑回归中,Sigmoid函数用于将线性回归的预测值转换为一个概率值,该概率值表示样本属于正类的可能性。
[ \sigma(z) = \frac{1}{1 + e^{-z}} ]
其中,( z ) 是线性回归的预测值,即 ( z = W \cdot X^T + b ),其中 ( W ) 是权重向量,( X ) 是特征向量,( b ) 是偏置项。
🎈逻辑回归模型
逻辑回归模型使用Sigmoid函数将线性回归的预测值转换为概率值,然后用这个概率值来预测样本的类别。对于二分类问题,如果概率值大于0.5,则预测为正类(标签为1),否则预测为负类(标签为0)。
📕损失函数与优化

🎈损失函数
逻辑回归使用交叉熵损失函数(Cross-Entropy Loss)来衡量模型预测的概率分布与真实概率分布之间的差异。对于二分类问题,交叉熵损失函数的公式如下:
[ J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_{\theta}(x^{(i)}))] ]
其中,( m ) 是样本数量,( y{(i)} ) 是第 ( i ) 个样本的真实标签(0或1),( h_{\theta}(x{(i)}) ) 是模型对第 ( i ) 个样本的预测概率。
🚀优化算法
为了最小化损失函数,我们需要使用优化算法来更新模型的参数(权重和偏置项)。常用的优化算法包括梯度下降(Gradient Descent)、随机梯度下降(Stochastic Gradient Descent, SGD)、批量梯度下降(Mini-Batch Gradient Descent)以及更先进的优化算法如Adam等。
逻辑回归(Logistic Regression)在多个实际场景中都有广泛的应用。下面我将列举几个典型的应用场景,并给出一个使用Python的scikit-learn库实现逻辑回归的代码示例。
🔍逻辑回归的应用场景

- 垃圾邮件分类:识别电子邮件是否为垃圾邮件。
- 疾病预测:根据患者的医疗记录预测是否患有某种疾病。
- 客户流失预测:预测客户是否会停止使用某个服务或产品。
- 金融欺诈检测:识别信用卡欺诈交易。
- 广告点击率预测:预测用户是否会点击某个广告。
🍀使用逻辑回归预测客户流失
假设我们有一个关于电信客户的数据集,我们想要预测哪些客户可能会流失(即停止使用服务)。
首先,确保你已经安装了pandas、scikit-learn和matplotlib等库。如果没有,可以使用pip进行安装:
pip install pandas scikit-learn matplotlib
然后,你可以使用以下Python代码来加载数据、训练逻辑回归模型并进行预测:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
import matplotlib.pyplot as plt # 加载数据(这里假设你有一个名为'customer_churn.csv'的数据集)
data = pd.read_csv('customer_churn.csv') # 假设'Churn'列是我们要预测的目标列(流失=1,未流失=0)
# 假设其他列是特征列,如'TotalCharges', 'tenure', 'MonthlyCharges'等
X = data.drop('Churn', axis=1) # 特征列
y = data['Churn'] # 目标列 # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建逻辑回归模型实例
model = LogisticRegression() # 训练模型
model.fit(X_train, y_train) # 预测测试集
y_pred = model.predict(X_test) # 评估模型性能
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred)) # 可视化混淆矩阵(可选)
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(10, 7))
plt.imshow(cm, cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.xticks(range(2), ['Not Churn', 'Churn'])
plt.yticks(range(2), ['Not Churn', 'Churn'])
plt.show()
注意:上述代码是一个示例,你需要根据你的具体数据集进行相应的调整。特别是,你需要确保你的数据已经被适当地预处理(如缺失值处理、特征缩放、分类特征编码等),并且你已经选择了合适的特征来训练模型。此外,你可能还需要调整逻辑回归模型的参数(如正则化强度、优化算法等)以获得最佳性能。

使用scikit-learn库实现逻辑回归示例
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, classification_report # 加载数据
data = pd.read_csv('data.csv')
X = data.drop('target', axis=1) # 特征列
y = data['target'] # 目标列(假设是二分类问题,标签为0和1) # 数据预处理(可选,但通常推荐进行特征缩放)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42) # 创建逻辑回归模型实例
model = LogisticRegression() # 训练模型
model.fit(X_train, y_train) # 预测测试集
y_pred = model.predict(X_test) # 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy}')
print(classification_report(y_test, y_pred))
在上面的代码中,我们首先加载了数据集,并将特征列和目标列分开。然后,我们使用了StandardScaler对特征进行了缩放(这是一个可选步骤,但通常有助于提高模型的性能)。接下来,我们使用了train_test_split函数将数据集划分为训练集和测试集。然后,我们创建了一个逻辑回归模型实例,并使用训练数据对其进行了训练。最后,我们使用测试集对模型进行了评估,并输出了模型的准确率和分类报告。
注意:在实际应用中,可能还需要进行更多的数据预处理步骤(如处理缺失值、编码分类特征等),以及调整模型的参数(如正则化强度、优化算法等)以优化模型的性能。
🔍逻辑回归的优缺点
🚀逻辑回归优点
- 易于理解和实现:逻辑回归模型简单直观,易于理解和解释。它基于线性回归模型,通过Sigmoid函数将线性回归的预测值转换为概率值,从而进行二分类。
- 计算效率高:逻辑回归的计算效率很高,因为它只需要计算输入特征的线性组合和Sigmoid函数。这使得逻辑回归在处理大规模数据集时非常有效。
- 模型的可解释性强:逻辑回归的系数(权重)可以被解释为特征对预测结果的重要性。较高的权重值意味着该特征对预测结果的影响较大。这使得逻辑回归在需要解释模型预测结果的场景中非常有用。
- 适用于二分类问题:逻辑回归特别适用于二分类问题,能够直接输出预测类别的概率值。
- 鲁棒性:逻辑回归对数据的分布没有严格的要求,不需要假设数据服从特定的分布(如正态分布)。这使得逻辑回归在实际应用中具有较强的鲁棒性。
📕逻辑回归缺点
- 对非线性问题处理不佳:逻辑回归是基于线性回归的,因此它对于非线性问题的处理能力有限。如果数据之间存在复杂的非线性关系,逻辑回归可能无法很好地拟合数据。
- 对特征相关性敏感:逻辑回归在处理具有多重共线性(特征之间存在高度相关性)的数据时,可能会出现不稳定的结果。因此,在使用逻辑回归之前,通常需要检查并处理特征之间的相关性。
- 容易欠拟合:当特征空间很大且数据维度较高时,逻辑回归可能会因为模型复杂度不足而欠拟合。这可以通过添加正则化项(如L1或L2正则化)来缓解,但这也需要权衡正则化强度和模型复杂度之间的关系。
- 对异常值敏感:逻辑回归对异常值较为敏感,因为异常值可能会影响模型的拟合效果。因此,在使用逻辑回归之前,通常需要对数据进行清洗和预处理,以去除或减轻异常值的影响。
- 不适用于多分类问题:虽然逻辑回归可以扩展到多分类问题(如使用softmax函数),但在处理多分类问题时,其性能可能不如其他专门为多分类问题设计的算法(如支持向量机、随机森林等)。
🎈逻辑回归缺点的优化方法
- 特征选择:
- 原理:从原始特征中选择与目标变量相关性较强的特征,以减少冗余特征和噪声特征的影响,提高模型的泛化能力。
- 优点:能够降低模型复杂度,提高预测准确性,减少计算成本。
- 正则化:
- 原理:通过L1正则化、L2正则化等方式,限制模型的复杂度,防止过拟合。
- 优点:能够有效控制模型的复杂度,提高模型的泛化能力,特别是在样本量不足或特征过于复杂的情况下。
- 集成学习:
- 原理:通过集成多个分类器的结果,提高模型的准确率和鲁棒性。
- 优点:可以综合多个模型的优点,提高整体预测性能,并减少单一模型可能存在的偏差。
- 改进模型结构:
- 原理:通过改变模型结构,如增加网络深度、增加隐藏层、改变激活函数等方式,提高模型的表达能力。
- 优点:对于非线性可分的数据,改进模型结构可以使其更好地拟合数据,提 高预测准确性。
- 数据增强:
- 原理:通过对数据进行扩增、旋转、缩放等方式,增加数据的多样性,提高模型的泛化能力。
- 优点:能够丰富训练数据,使得模型能够更好地学习到数据的内在规律,提高预测性能。
- 处理异常值:
- 原理:在数据预处理阶段,对异常值进行处理,如删除、替换或缩放等。
- 优点:能够减少异常值对模型预测结果的影响,提高模型的鲁棒性。
- 处理多分类问题:
- 原理:对于多分类问题,可以通过一些技术(如One-vs-All)进行处理,将多分类问题转化为多个二分类问题。
- 优点:使得逻辑回归能够应用于多分类场景,扩大其应用范围。
综上所述,针对逻辑回归的缺点,可以通过特征选择、正则化、集成学习、改进模型结构、数据增强、处理异常值和处理多分类问题等方法进行优化。这些方法能够提高模型的预测性能、泛化能力和鲁棒性,使其在实际应用中更加有效和可靠。
相关文章:

逻辑回归(Logistic Regression)及其在机器学习中的应用
🚀时空传送门 🔍逻辑回归原理📕Sigmoid函数🎈逻辑回归模型 📕损失函数与优化🎈损失函数🚀优化算法 🔍逻辑回归的应用场景🍀使用逻辑回归预测客户流失使用scikit-learn库实…...

【计算机视觉】人脸算法之图像处理基础知识【七】
直方图均衡化 直方图均衡化是一种常用的图像处理技术,用于改善图像的对比度,特别是在图像的细节被埋没在暗部或亮部区域时。通过重新分配图像的像素强度值,使得图像的整体对比度增强,从而让更多的细节变得可见。 import cv2 imp…...
家政预约小程序14权限配置
目录 1 创建用户2 创建角色3 启用登录4 实现退出总结 我们现在小程序端的功能基本开发好了,小程序开发好之后需要给运营人员提供管理后台,要分配账号、配置权限,我们本篇就介绍一下权限如何分配。 1 创建用户 在微搭中,用户分为内…...

解决 vue 项目一直出现 sockjs-node/info?t=问题
其实如果是在开发环境,应该是开发的时候网络环境变更导致,比如你切换无线网络,导致开发服务器的IP地址换了,这样开发服务器会不知道如何确定访问源。开发环境中关闭npm dev server,然后重新npm run serve重新构建服务环…...
麒麟信安系统关闭core文件操作
在使用麒麟信安系统时,如果应用程序运行过程中崩溃了,此时并不会导致内核崩溃,只会在tmp目录下产生崩溃数据,如下图 不过tmp目录下的分区容量有限,当崩溃的应用core文件过大时将会占用tmp空间,导致tmpfs分区…...

微信小程序轮播图
效果图 详情可见 微信小程序 参照:swiper | uni-app官网 代码: <!--轮播图-- > <swiper interval"2000" autoplay"true" circular"true" style"height: 300px;"><swiper-item style&qu…...
redisson WRONGPASS invalid username-password pair or user is disable
1、技术架构:若依微服务框架 <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-dependencies</artifactId><version>2021.1</version></dependency> <dependency><…...

QT拖放事件之一:初识拖放4大事件处理函数
0、拖放 两个动作,合在一起称之为拖放事件; 拖:就是拖着走; 放:就是拖着走,然后松开鼠标了,释放了,这就是放; 注意:放:拖着的东西要放在什么地方??? 假如,我将一个记事本拖着跑,然后放到一个Widget窗口上,那么为了使得Widget能感知相应的事件(拖着进入事件…...

使用Python进行数据可视化:从基础到高级
使用Python进行数据可视化:从基础到高级 数据可视化是数据分析过程中不可或缺的一部分,通过图形化的方式展示数据,可以更直观地发现数据中的趋势和模式。Python凭借其丰富的库和强大的功能,成为数据可视化的首选编程语言。本文将介绍数据可视化的基础概念、常用的Python库…...
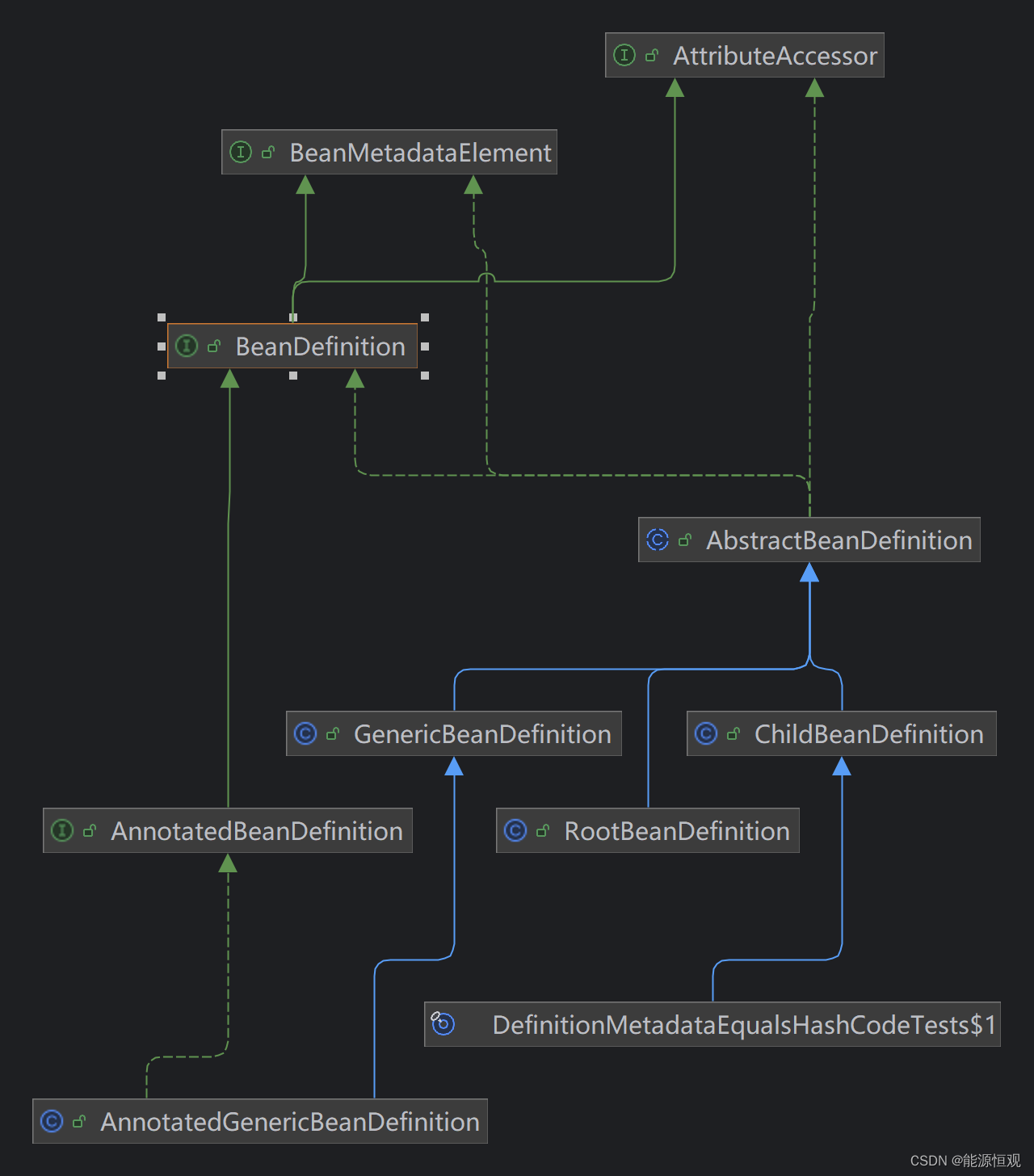
【十二】图解 Spring 核心数据结构:BeanDefinition
图解 Spring 核心数据结构:BeanDefinition 简介 使用spring框架的技术人员都知道spring两个大核心技术IOC和AOP,随着投入更多的时间去学习spring生态,越发觉得spring的发展不可思议,一直都是引领着Java EE的技术变革,这…...

速盾:阿里云ddos黑洞是怎么回事?
阿里云ddos黑洞是一种防御分布式拒绝服务(DDoS)攻击的安全机制。DDoS攻击是指利用大量的合法请求占用目标服务器的资源,从而使服务器无法正常响应合法用户的请求。为了应对这种攻击,阿里云引入了黑洞机制。 黑洞机制是一种主动防…...
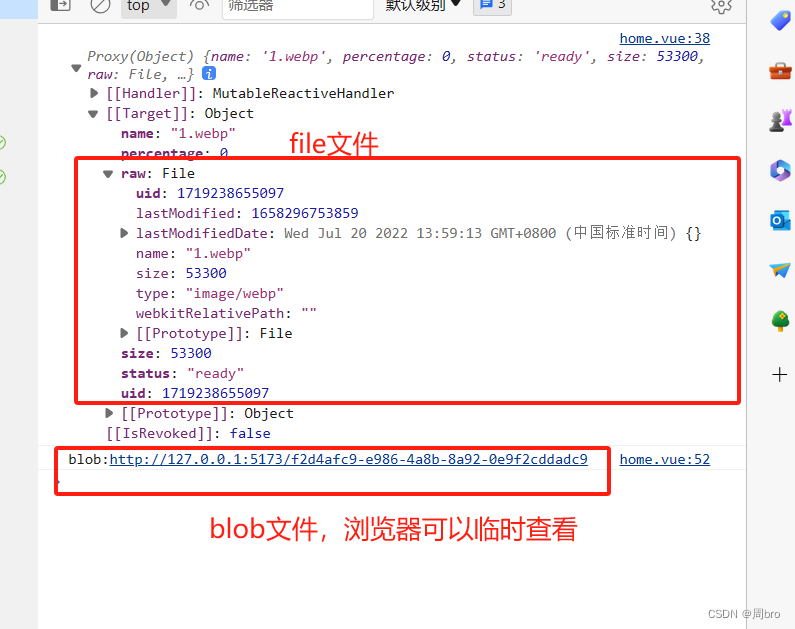
File文件转Blob文件,临时路径浏览器可查看
fileToBlob (file) { var reader new FileReader(); reader.readAsArrayBuffer(file); reader.onload function (event) { let blob new Blob([event.target.result], { type: file.type }); //{ type: file.type } 预览blob发现乱码可能是type不对 要获取file文件的type …...

区块链行业DDOS防护痛点在哪
区块链行业DDOS防护痛点在哪?随着区块链技术的迅猛发展,其应用场景已经从最初的数字货币扩展到了金融、供应链、物联网等多个领域。然而,随着区块链行业的快速崛起,其所面临的网络安全威胁也日益严重,尤其是DDoS(分布…...
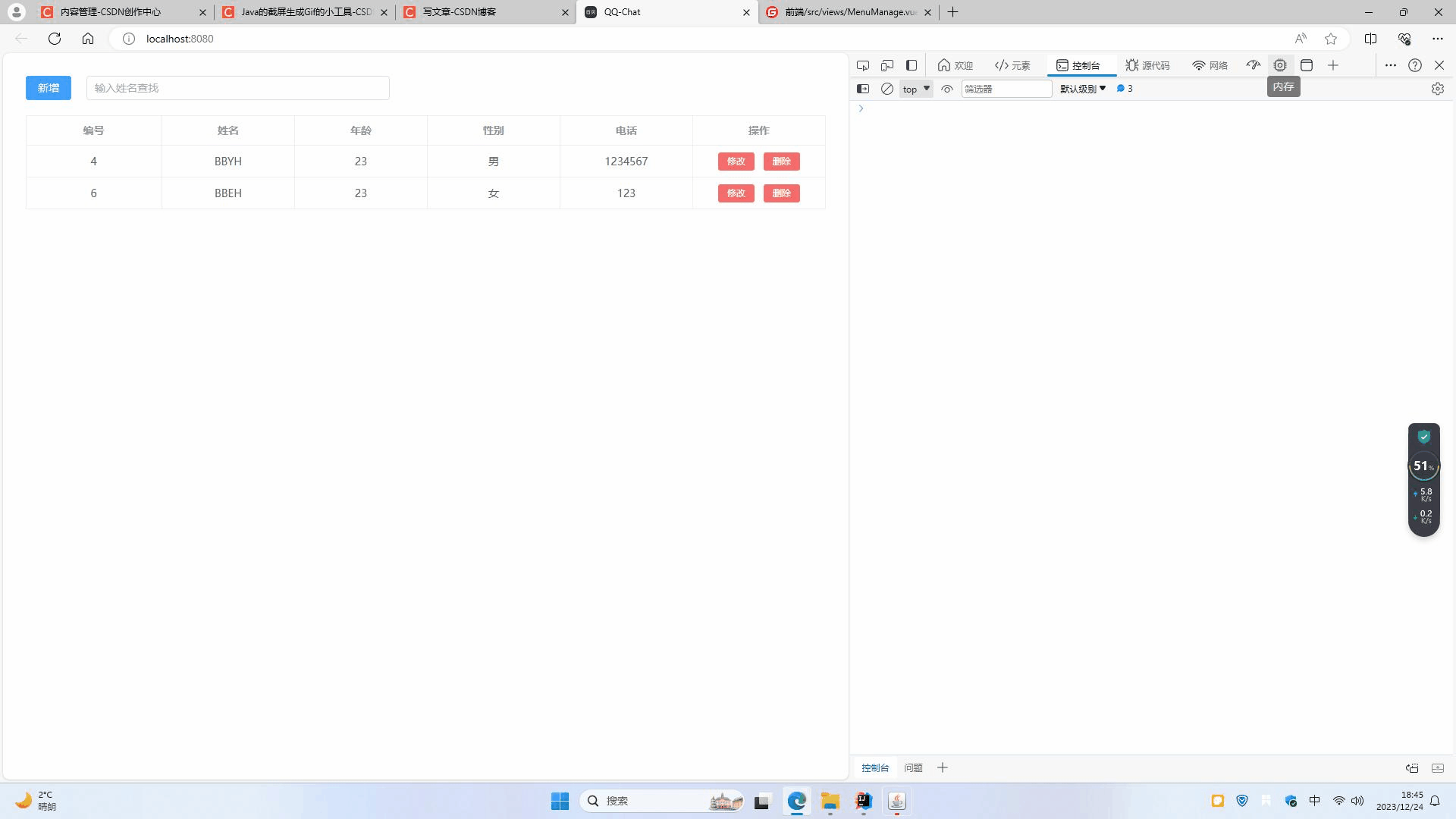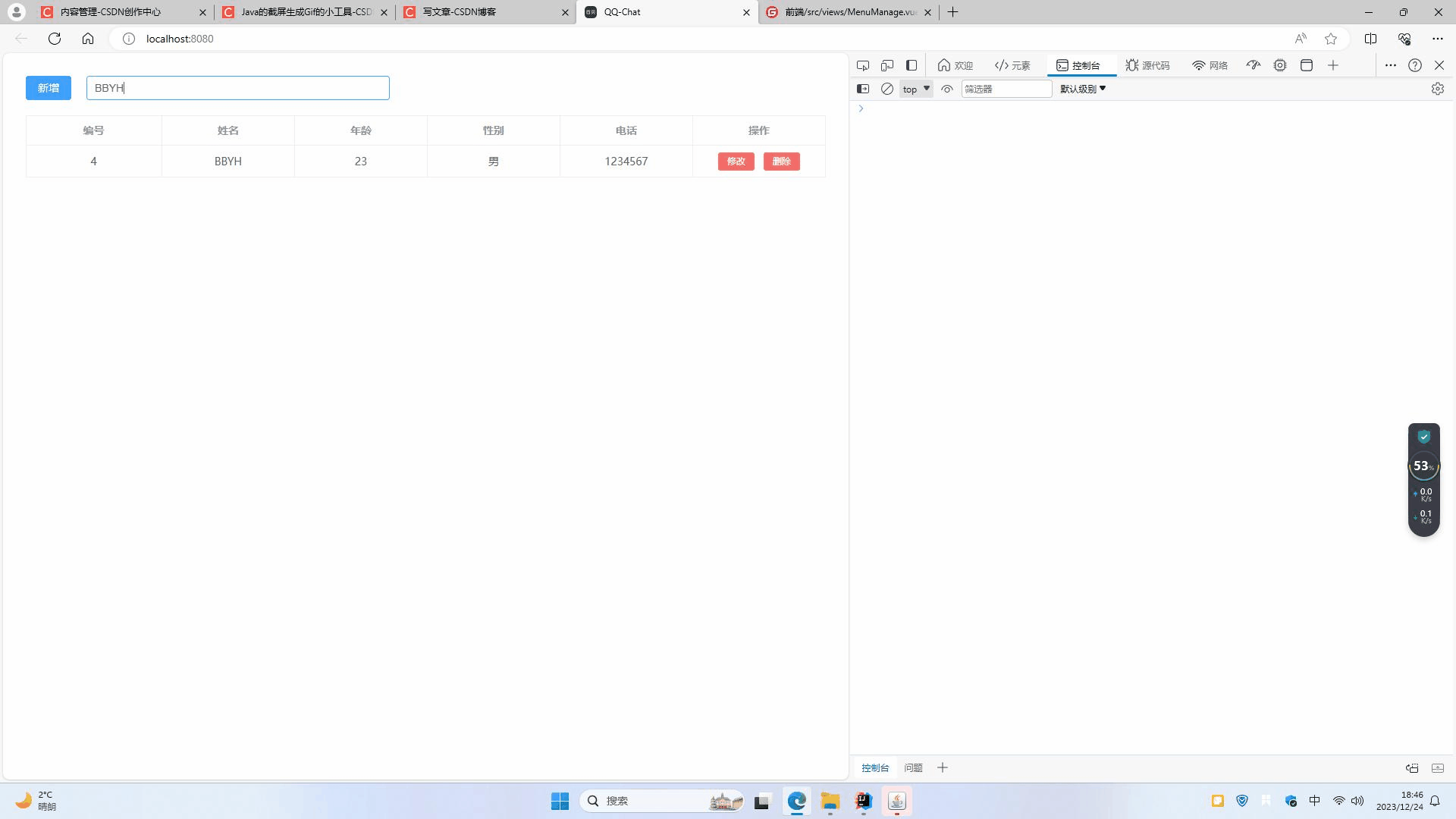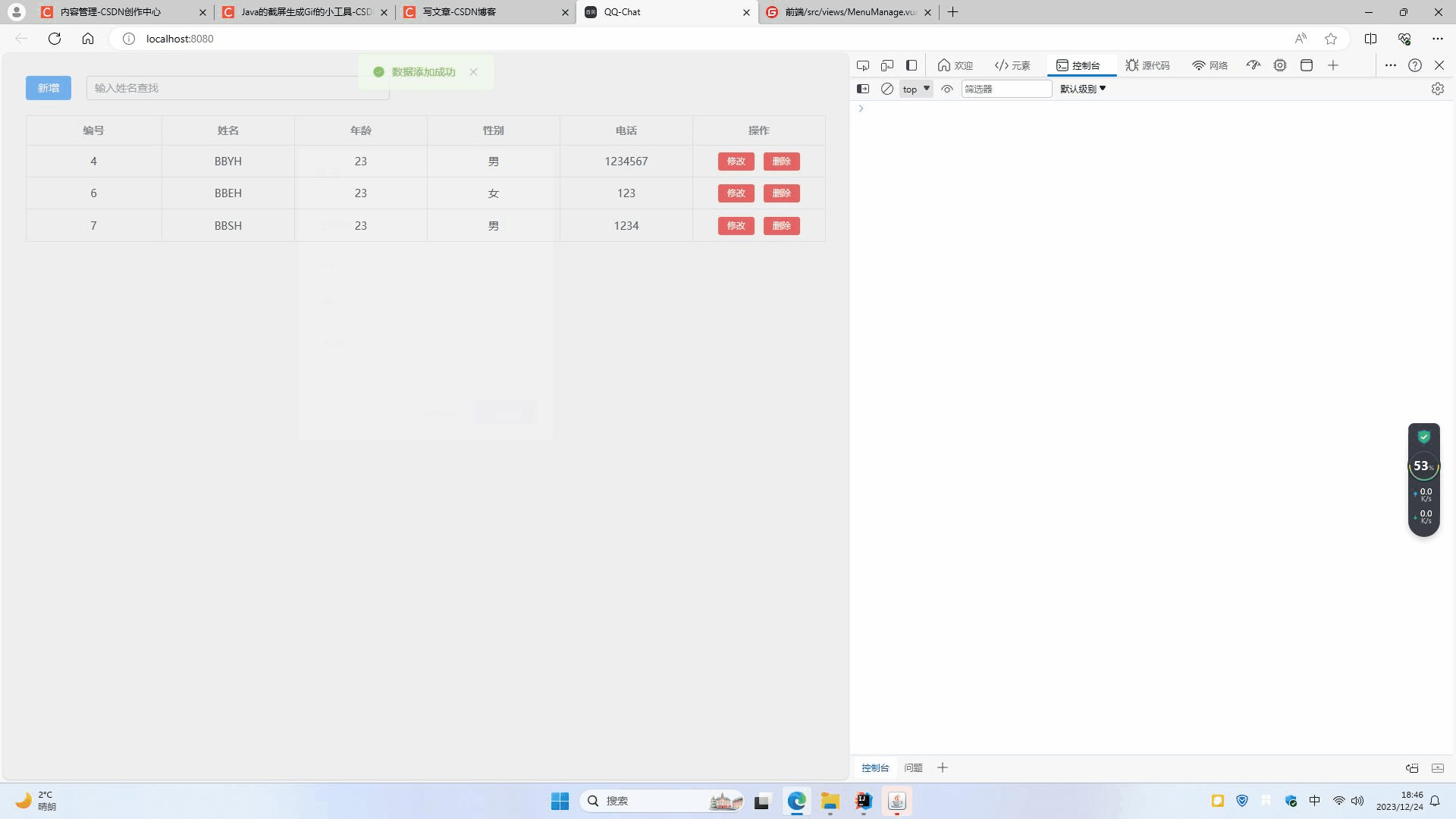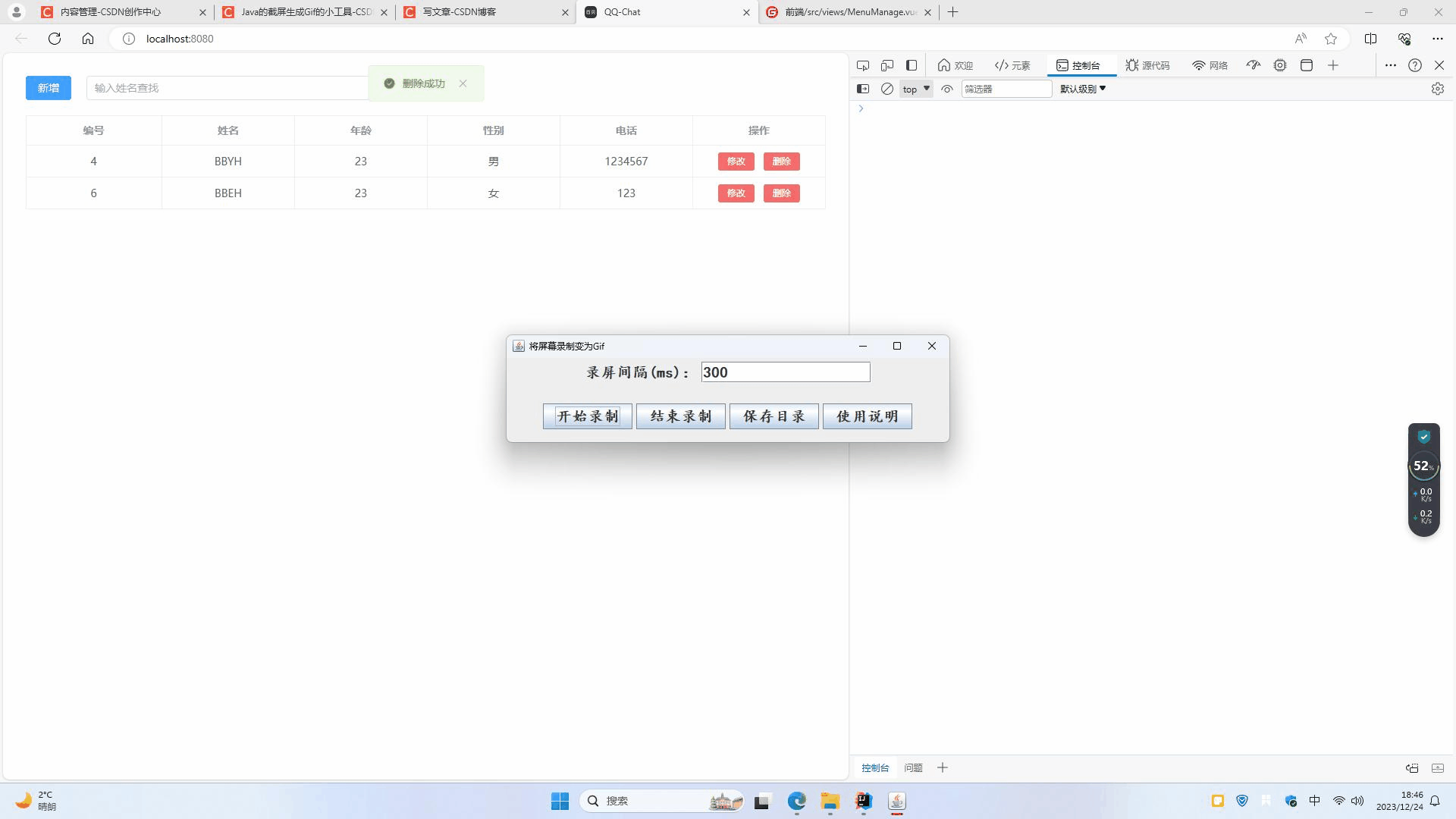
浏览器自带的IndexDB的简单使用示例--小型学生管理系统
浏览器自带的IndexDB的简单使用示例--小型学生管理系统 文章说明代码效果展示 文章说明 本文主要为了简单学习IndexDB数据库的使用,写了一个简单的增删改查功能 代码 App.vue(界面的源码) <template><div style"padding: 30px&…...

2024年计算机专业还值得选吗?
个人认为可以 一、就业前景广阔 市场需求旺盛:随着数字化和信息化的快速发展,计算机技术已经渗透到各个行业和领域。无论是传统制造业、金融、医疗,还是新兴的互联网、人工智能等领域,都离不开计算机专业人才的支持。因此&#x…...

JSON.parse(JSON.stringify())导致的响应式属性丢失
console.log("formdata赋值前", this.formdata);console.log("row",row);console.log("row序列化后", JSON.parse(JSON.stringify(row)));this.formdata JSON.parse(JSON.stringify(row)); console.log("formdata赋值后", this.formd…...
SpringBoot引入外部依赖包
将需要引入的文件放置到与src同级别的目录下 如上,在src的同级,新建了一个lib目录,将jar包放置其中 在POM文件下,加入如下配置 <dependency><groupId>com.aliyun</groupId><artifactId>com.aliyun.filed…...
Spring事务介绍、Spring集成MyBatis
目录 1.Spring的事务1.1 什么是事务?1.2 事务的特性(ACID)1.3 Spring 事务实现方式有哪些?1.4 Spring事务管理接口介绍1.4.1 PlatformTransactionManager:事务管理接口1.4.2 TransactionDefinition:事务属性事务管理器接口1.4.3 T…...

使用GPG来解密和加密文件详解
文章目录 使用私钥解密文件示例步骤 注意事项加密文件前提条件导入公钥加密文件输出加密文件示例步骤注意事项邮箱不是必须的情况1:有多个公钥情况2:只有一个公钥示例步骤示例1:指定公钥ID或邮箱地址示例2:密钥环中只有一个相关的…...

【Flutter】基础教程:从安装到发布
Flutter 是一种流行的开源移动应用开发框架,由 Google 开发,可用于构建高性能、跨平台的移动应用。本教程将带领你从安装 Flutter 开发环境开始,一步步完成第一个程序,并介绍如何将应用发布到各个平台上。 跨端原理的关键点包括&a…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
