【数据结构与算法】最短路径,Floyd算法,Dijkstra算法 详解
Floyd算法
for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (d[i][k] != INF && d[k][j] != INF) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}
}
Dijkstra算法(基于最小堆)
void dijkstra(int start) {vis.reset();// 初始化for (int i = 0; i < n; i++) {if (i == start) {dist[i] = 0;hmin.push({i, 0});} else {dist[i] = INF;prior[i] = -1;}}while (hmin.size()) {auto t = hmin.top();hmin.pop();int u = t.v;int du = t.d;if (vis[u]) {continue;}vis[u] = 1;// 访问邻接节点for (int i = head[u]; ~i; i = edge[i].next) {int v = edge[i].to;if (dist[v] > du + 1) {// 更新最短距离dist[v] = du + 1;prior[v] = u;hmin.push({v, du + 1});}}}
}
Dijkstra算法和弗洛伊德(Floyd)算法是如何求最短路径的?两种算法各自的优缺点是什么?
-
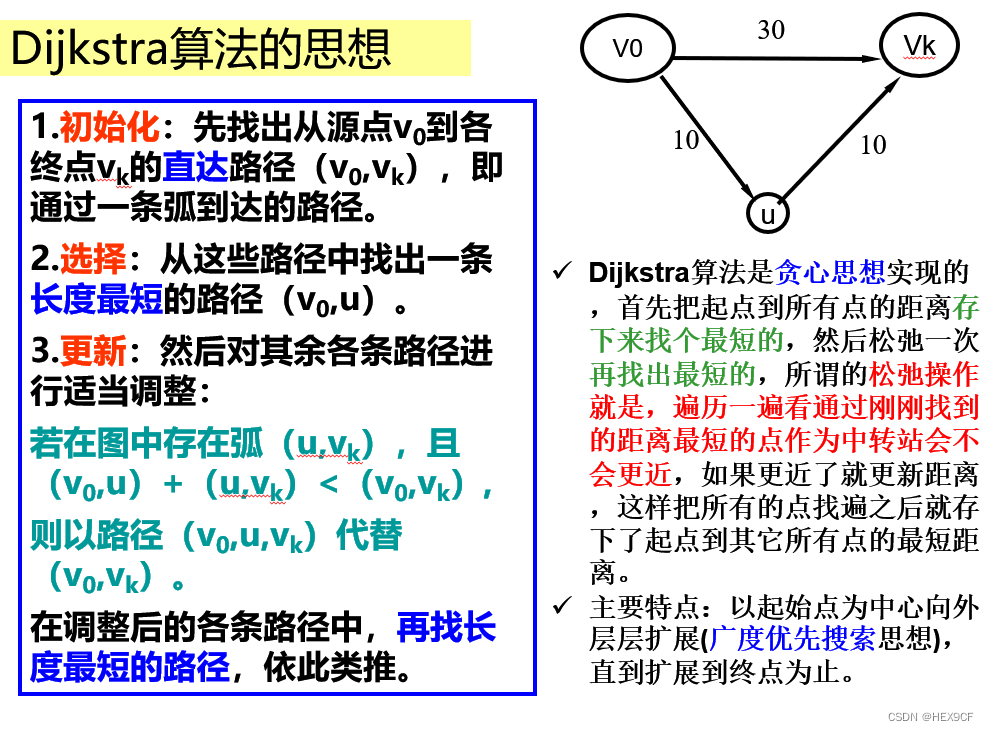
Dijkstra算法:是一种单源最短路径算法,即从图中的一个节点到其他所有节点的最短路径。它的基本思想是每次找到离源节点最近的一个节点,然后以该节点为中心进行扩展,最终得到源节点到其他所有节点的最短路径。
- 优点:当只需要求解单源最短路径问题时,效率较高。
- 缺点:
- 不能处理存在负权边的图。
- 只能求解单源最短路径问题,不能求解多源最短路径问题。
-
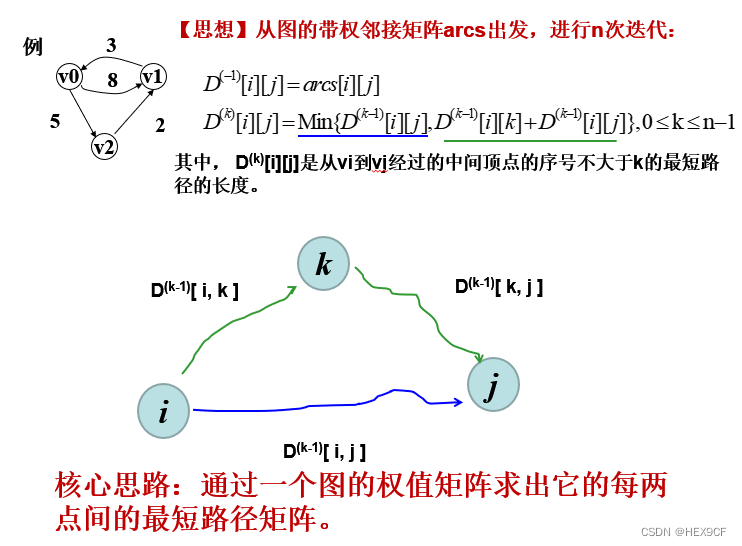
弗洛伊德(Floyd)算法:是一种多源最短路径算法,即求图中任意两点之间的最短路径。它的基本思想是从 vi 到 vj 的所有可能存在的路径中,选出一条长度最短的路径。
- 优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。
- 缺点:时间复杂度比较高,不适合计算大量数据。
相关文章:

【数据结构与算法】最短路径,Floyd算法,Dijkstra算法 详解
Floyd算法 for (int k 0; k < n; k) {for (int i 0; i < n; i) {for (int j 0; j < n; j) {if (d[i][k] ! INF && d[k][j] ! INF) {d[i][j] min(d[i][j], d[i][k] d[k][j]);}}} }Dijkstra算法(基于最小堆) void dijkstra(int st…...

PHP中如何进行网络爬虫和数据抓取?
随着互联网时代的到来,网络数据的爬取与抓取已成为许多人的日常工作。在支持网页开发的程序语言中,php以其可扩展性和易上手的特点,成为了网络爬虫和数据抓取的热门选项。本文将从以下几个方面介绍php中如何进行网络爬虫和数据抓取。 一、HT…...
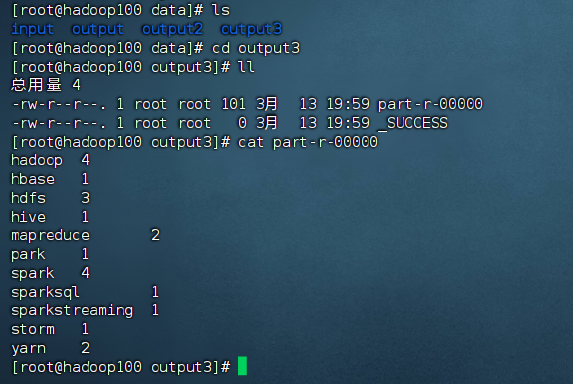
【Hadoop集群搭建】实验3:JDK安装及配置、Hadoop本地模式部署及测试
1. 安装 SSH 工具 SSH Secure Shell Client 传输软件 FinalShell(推荐使用) 1.1使用SSH工具将JDK安装包上传至虚拟主机hadoop01, hadoop02, hadoop03,sogou500w 数据上传至 hadoop01。 a. 在虚拟主机/usr 目录下创建文件夹 java,JDK 上传至此目录&…...

分布式锁在Spring Boot应用中的优雅实现
在现代微服务架构中,分布式锁是一种常用的技术手段,用于确保在分布式系统中,同一时间只有一个服务实例能够执行某个特定的操作。这对于防止并发问题、保证数据一致性至关重要。在Spring Boot应用中,我们可以通过自定义注解和切面的…...

常用框架-Spring Boot
常用框架-Spring Boot 1、Spring Boot是什么?2、为什么要使用Spring Boot?3、Spring Boot的核心注解是哪个?它主要由哪几个注解组成的?4、有哪些运行Spring Boot的方式?5、如何理解 Spring Boot 中的Starters?6、有哪些常见的Starters?7、如何在Spring Boot启动的时候运…...

AttributeError: module ‘cv2‘ has no attribute ‘face‘
Traceback (most recent call last): File "D:\AI_37\pythonProject7\day23\课堂代码\day23\07-人脸识别.py", line 4, in <module> recognizer cv2.face.LBPHFaceRecognizer_create() ^^^^^^^^ AttributeError: module cv2 has no at…...

不管你是普本还是双一流,建议你一定要尝试一下学习GIS开发
毕业季,很多企业的秋招和暑期实习已经开始了,在这个24秋招和25考研并列进行的毕业季,GIS专业的同学,做好自己的职业规划显得十分重要。 WebGIS开发,近年来成为了3S及相关专业的学生备受关注的热门选择。 不论是本科毕…...

OurBMC大咖说丨第5期:BMC开发中的非标准化问题探讨
栏目介绍:"OurBMC大咖说" 是由 OurBMC 社区精心策划的线上讲座栏目,邀请 BMC 相关领域大咖共同探讨 BMC 全栈技术的发展趋势、挑战和机遇。无论你是初学者还是资深从业者,"OurBMC大咖说" 都将为你提供一个宝贵的学习和交…...

空调制冷剂泄漏引发健康隐患,冷媒传感器实时监测至关重要
随着夏季的脚步逐渐临近,气温逐渐攀升,空调成为了许多家庭和企业必不可少的降温设备。然而,近年来多起因空调制冷剂泄漏导致的健康问题和安全事故,让人们开始重新审视空调使用安全的重要性。其中,冷媒传感器的实时监测…...

开源TinyFSM状态机适用于嵌入式工业平台吗?
文章目录 引言基于传统 C 实现的状态机TinyFSM 实现的对比现代 C 实现的状态机性能对比TinyFSM 性能测试传统 C 性能测试现代 C 性能测试 工业Misra C编程标准TinyFSM 的优缺点分析结论 引言 TinyFSM是一个为C设计的轻量级有限状态机开源库库。 在嵌入式系统开发中,…...
EE trade:利弗莫尔三步建仓法
在股市投资领域,利弗莫尔这个名字代表着无数的智慧和经历。他的三步建仓法成为了投资者们趋之若鹜的学习对象。本文将详细解析利弗莫尔的著名买入法,通过分步进攻方式,有效掌控市场并实现盈利。 一、利弗莫尔的三步建仓法详解 利弗莫尔三步…...

Java中Callable的应用
在Java中,Callable接口是一种用于并发编程的接口,它与Runnable类似,但有一些重要的区别和优势。Callable接口提供了一种在多线程环境下执行任务并返回结果的方法。以下是一些Callable接口的常见应用场景和使用示例: Callable vs.…...
测试卡无法仪表注册问题分析
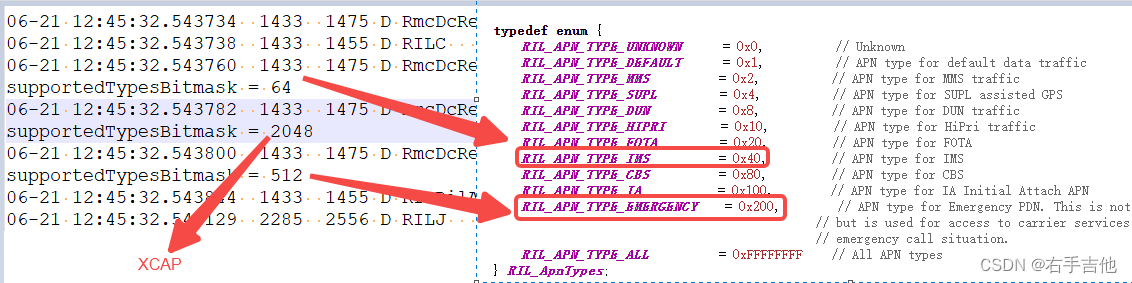
1、问题描述 00101测试卡无法注册LTE网络,modemlog中发现终端未发起Attach请求,对比正常注册非正常注册的版本,发现正常的多出了ims apn。可以通过ATCGDCONT?来查询modem APN参数。 2、问题分析 目前Modem是一套,没有相关修改。因…...

【扩散模型(一)】Stable Diffusion中的重建分支(reconstruction branch)和条件分支(condition branch)
Stable Diffusion 是一种基于扩散模型的生成模型,用于生成图像等数据。在解释 Stable Diffusion 的过程中,经常会提到两个主要的分支:重建分支(reconstruction branch)和条件分支(condition branch…...

WPF——Binding
一、作用 将Window GUI的运行机理从 “事件驱动” 转变为 “数据驱动”。将UI界面与业务逻辑解耦,使得改动一个而无需改动另一个。数据逻辑层自成体系,使得无需借助UI也可进行单元测试。 二、基础 1. Binding源模板 Binding包括源与目标,源…...
linux与windows环境下qt程序打包教程
一、演示环境 qt5.14.2 二、Linux 2.1 关联依赖文件 2.1.1 下载打包工具 在Windows环境下可以使用 Qt Creator自带的官方工具进行打包,而Linux环境下没有官方工具,需要借助第三方工具才能打包。如:linuxdeployqt、CQtDeployer、AppImage…...

LeetCode21-合并两个有序链表
题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4] 示例 2: 输入:l1 [], l2 [] 输出…...
——day47)
嵌入式学习——数据结构(双向无头无环链表)——day47
1. makefile——(注意:双向无头链表第一个节点的pre为空,最后一个节点的next为空) 单向无头链表只能找到后一个节点、双向无头链表前后节点都能找到 OBJ:doulink OBJSmain.c doublelink.c CClgcc$(OBJ):$(OBJS)$(CC) $^ -o $ .PH…...
MYSQL 将某个字段赋值当前时间
如 我们需要将use_time 赋值为当前时间: 准备三条数据 : 执行sql ,2种当前时间赋值函数,1种关键字赋值 : update test_info SET use_timeNOW() WHERE id 1; update test_info SET use_timeCURRENT_TIMESTAMP() …...

ModelSim® SE Command Reference Manual : find命令的用法
该命令按类型和名称定位对象。命令的参数按对象类型分组。 1、语法 find nets | signals <object_name> … [-internal] [-nofilter] {[-in] [-inout] [-out] | [-ports]} [-recursive]find instances | blocks {<object_name> … | -bydu <design_unit> |…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
