堆的实现详解
目录
- 1. 堆的概念和特点
- 2. 堆的实现
- 2.1 堆向下调整算法
- 2.2堆的创建
- 2.3 建堆时间复杂度
- 2.4 堆的插入
- 2.5 堆的删除
- 2.6 堆的代码实现
- 2.6.1 结构体
- 2.6.2 初始化
- 2.6.3 销毁
- 2.6.4 插入
- 2.6.5 删除
- 2.6.6 获取堆顶
- 2.6.7 判空
- 2.6.8 个数
- 2.6.9 向上调整
- 2.6.10 向下调整
- 3. 堆的实现测试
- 测试1
- 测试2
- 测试3
- 测试4
- 向上调整建堆测试5
- 向下调整建堆测试6
- 4. 堆的应用
- 4.1 堆排序
- 4.2 TOP-K问题
- 5. test.c文件
- 6. Heap.c
- 7. Heap.h
1. 堆的概念和特点
- 定义:
堆通常可以被看作是一棵完全二叉树的数组对象。这意味着堆的物理结构本质上是顺序存储的(线性的),但在逻辑上则表现为完全二叉树的逻辑存储结构。
堆总是满足堆性质:堆中某个结点的值总是不大于(最大堆)或不小于(最小堆)其父结点的值。 - 分类:
根据堆顶元素的大小,堆可以分为最大堆(大根堆)和最小堆(小根堆)。最大堆的根结点值是所有元素中的最大值,而最小堆的根结点值是所有元素中的最小值。
常见的堆类型还包括二叉堆和斐波那契堆等。 - 结构:
堆的物理结构是一维数组,数组的容量和元素个数是堆的重要属性。
在堆中,一个结点的父节点可以通过该结点的索引值整除2得到
2. 堆的实现
2.1 堆向下调整算法
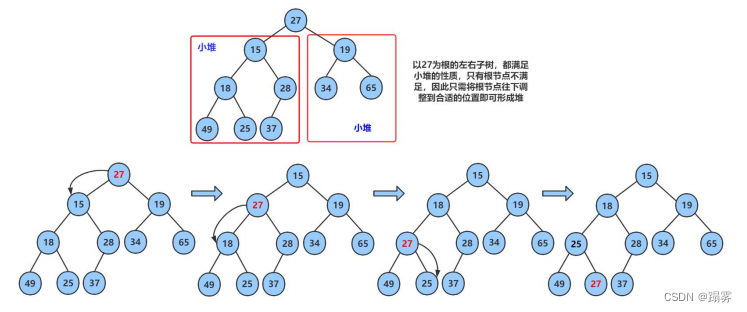
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};
2.2堆的创建
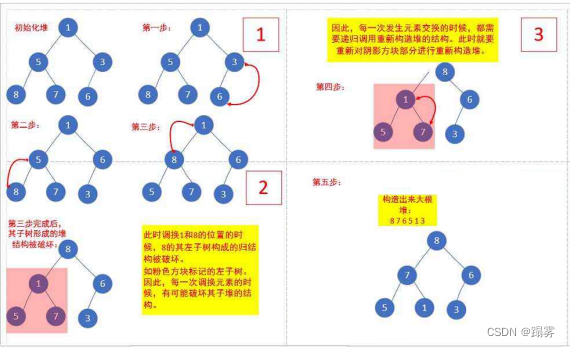
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
int a[] = {1,5,3,8,7,6};
2.3 建堆时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的
就是近似值,多几个节点不影响最终结果):
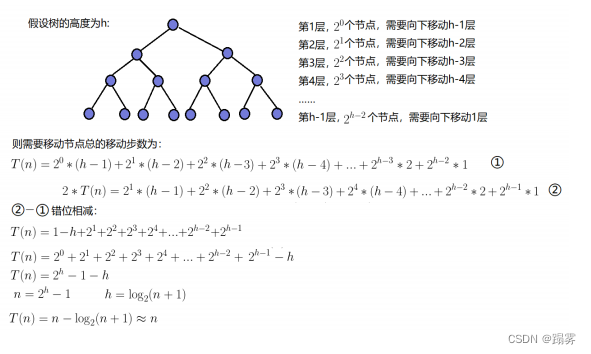
因此:建堆的时间复杂度为O(N)。
2.4 堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
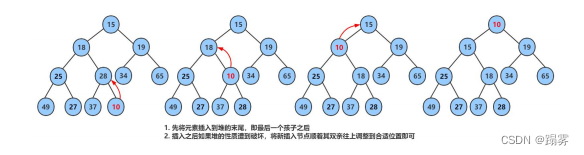
2.5 堆的删除
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
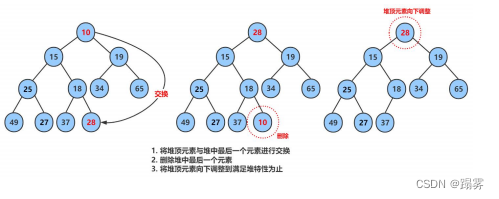
2.6 堆的代码实现
2.6.1 结构体
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
2.6.2 初始化
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}
2.6.3 销毁
//销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = 0;php->size = 0;
}
2.6.4 插入
//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("HeapPush");return;}php->a = tmp;php->capacity = newCapacity;}//插入数据php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a, php->size - 1);
}
2.6.5 删除
//删除堆顶的数据
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}
2.6.6 获取堆顶
//获取堆顶
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
2.6.7 判空
//判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
2.6.8 个数
//个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
2.6.9 向上调整
//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent; parent = (child - 1) / 2;}else{break;}}
}
2.6.10 向下调整
//向下调整
void AdjustDown(int* a, int n, int parent)
{//假设最小int child = parent * 2 + 1;while (child < n){//选出左右孩子小的那个if (child+1 < n && a[child + 1] < a[child]){child++;}//不用管哪个最小if (a[child] < a[parent]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
3. 堆的实现测试
测试1
//堆的实现测试
void HeapTest1()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };int sz = sizeof(a) / sizeof(a[0]);for (int i = 0; i < sz; i++){HeapPush(&hp, a[i]);}HeapDestroy(&hp);
}

测试2
void HeapTest1()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };int sz = sizeof(a) / sizeof(a[0]);for (int i = 0; i < sz; i++){HeapPush(&hp, a[i]);}HeapPop(&hp);HeapDestroy(&hp);
}

测试3
void HeapTest1()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };int sz = sizeof(a) / sizeof(a[0]);for (int i = 0; i < sz; i++){HeapPush(&hp, a[i]);}//HeapPop(&hp);while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d\n", top);HeapPop(&hp);}HeapDestroy(&hp);
}

测试4
//top-k问题
//方法1:弊端: 先有一个堆太麻烦,空间复杂度高还得拷贝数据。
void HeapSort(int* a, int n)
{HP hp;HeapInit(&hp);for (int i = 0; i < n; i++){HeapPush(&hp, a[i]);}int i = 0;while (!HeapEmpty(&hp)){int top = HeapTop(&hp);a[i++] = top;HeapPop(&hp);}HeapDestroy(&hp);
}

向上调整建堆测试5
void HeapSort2(int* a, int n)
{//升序-- 建小堆//降序-- 建大堆//向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}//向下调整建堆/*for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}*/int end = n - 1;while (end > 0){//交换Swap(&a[0], &a[end]);//再调整,选出次小的AdjustDown(a, end, 0);end--;}
}
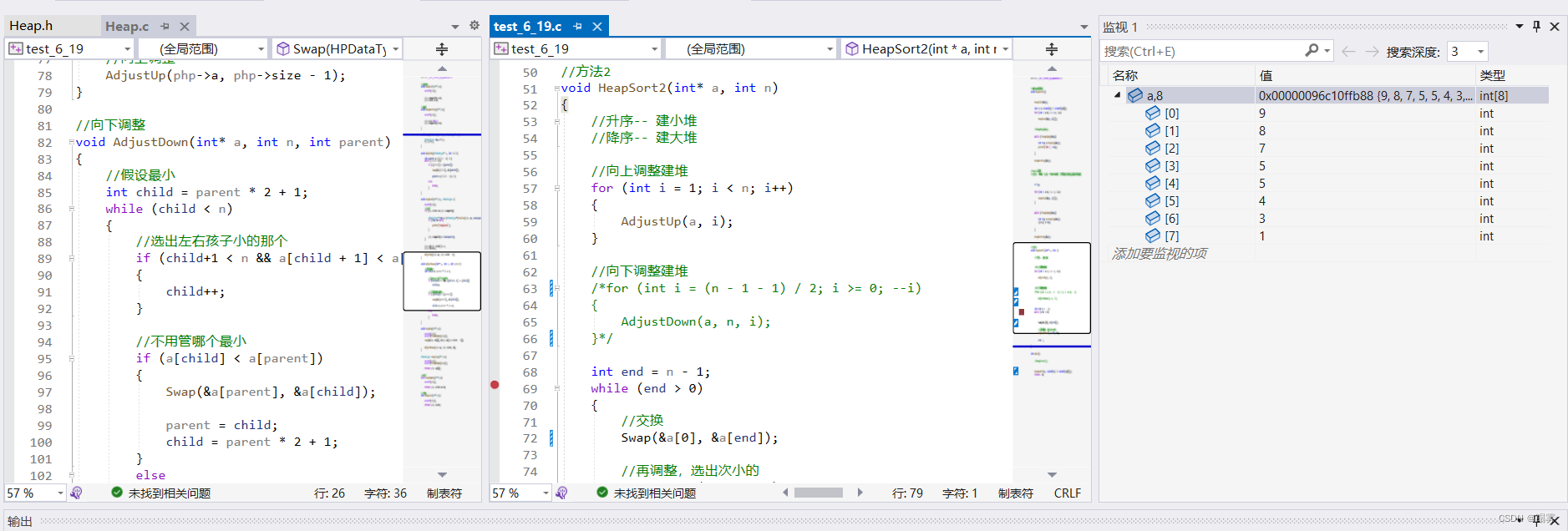
向下调整建堆测试6
//方法2
void HeapSort2(int* a, int n)
{//升序-- 建小堆//降序-- 建大堆//向上调整建堆/*for (int i = 1; i < n; i++){AdjustUp(a, i);}*///向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){//交换Swap(&a[0], &a[end]);//再调整,选出次小的AdjustDown(a, end, 0);end--;}
}
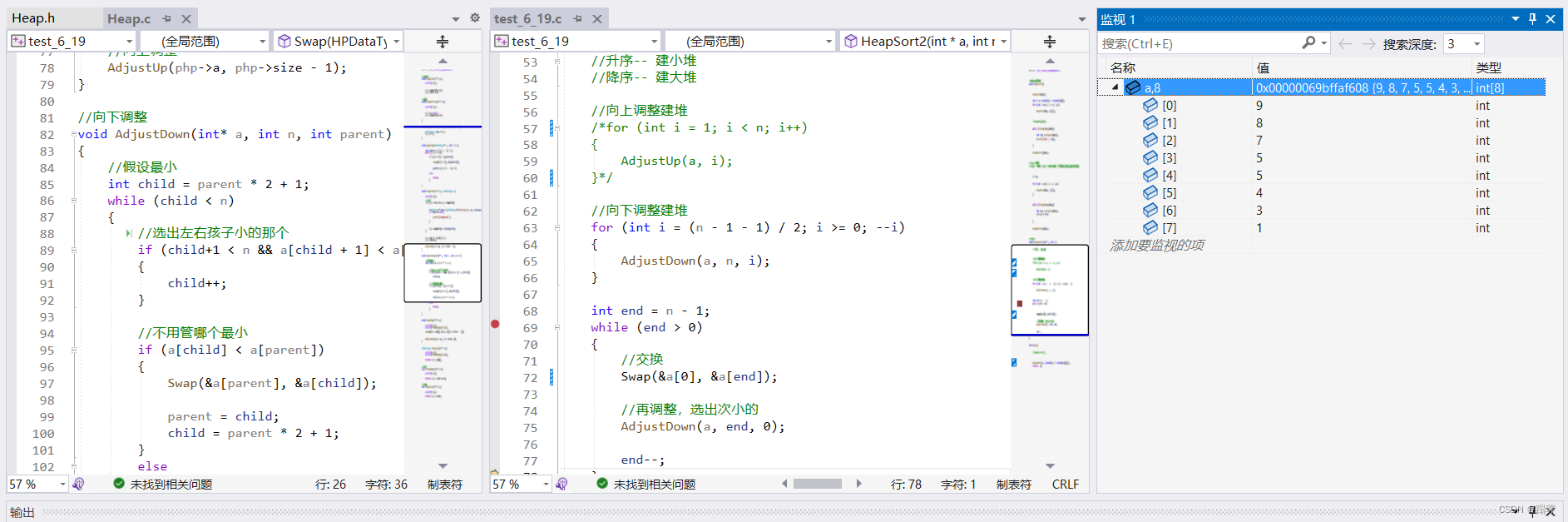
4. 堆的应用
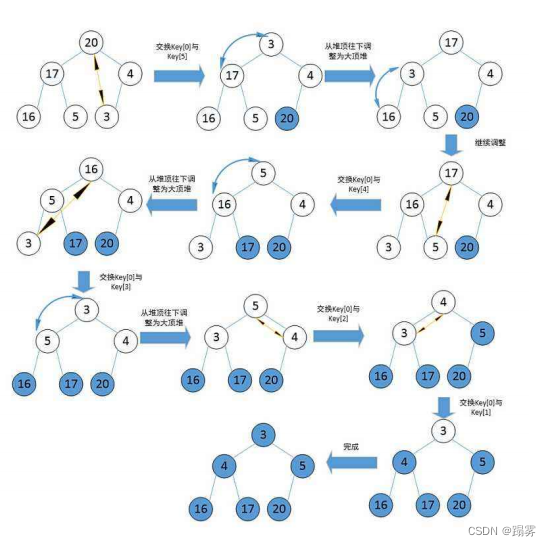
4.1 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
- 建堆
升序:建大堆
降序:建小堆 - 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
4.2 TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
5. test.c文件
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"//堆的实现测试
void HeapTest1()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };int sz = sizeof(a) / sizeof(a[0]);for (int i = 0; i < sz; i++){HeapPush(&hp, a[i]);}//HeapPop(&hp);while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d\n", top);HeapPop(&hp);}HeapDestroy(&hp);
}//top-k问题
//方法1:弊端: 先有一个堆太麻烦,空间复杂度高还得拷贝数据。
void HeapSort(int* a, int n)
{HP hp;HeapInit(&hp);for (int i = 0; i < n; i++){HeapPush(&hp, a[i]);}int i = 0;while (!HeapEmpty(&hp)){int top = HeapTop(&hp);a[i++] = top;HeapPop(&hp);}HeapDestroy(&hp);
}//方法2
void HeapSort2(int* a, int n)
{//升序-- 建小堆//降序-- 建大堆//向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}//向下调整建堆/*for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}*/int end = n - 1;while (end > 0){//交换Swap(&a[0], &a[end]);//再调整,选出次小的AdjustDown(a, end, 0);end--;}
}int main()
{//HeapTest1();int a[] = { 7,8,3,5,1,9,5,4 };HeapSort2(a, sizeof(a) / sizeof(a[0]));return 0;
}
6. Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}//销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = 0;php->size = 0;
}//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p2;*p2 = *p1;*p1 = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent; parent = (child - 1) / 2;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("HeapPush");return;}php->a = tmp;php->capacity = newCapacity;}//插入数据php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a, php->size - 1);
}//向下调整
void AdjustDown(int* a, int n, int parent)
{//假设最小int child = parent * 2 + 1;while (child < n){//选出左右孩子小的那个if (child+1 < n && a[child + 1] < a[child]){child++;}//不用管哪个最小if (a[child] < a[parent]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}//删除堆顶的数据
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}//获取堆顶
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}//判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}//个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
7. Heap.h
#pragma once#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <stdio.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//初始化
void HeapInit(HP* php);//销毁
void HeapDestroy(HP* php);//插入
void HeapPush(HP* php, HPDataType x);//删除
void HeapPop(HP* php);//获取堆顶
HPDataType HeapTop(HP* php);//判空
bool HeapEmpty(HP* php);//个数
int HeapSize(HP* php);//向上调整
void AdjustUp(HPDataType* a, int child);//向下调整
void AdjustDown(int* a, int n, int parent);
相关文章:

堆的实现详解
目录 1. 堆的概念和特点2. 堆的实现2.1 堆向下调整算法2.2堆的创建2.3 建堆时间复杂度2.4 堆的插入2.5 堆的删除2.6 堆的代码实现2.6.1 结构体2.6.2 初始化2.6.3 销毁2.6.4 插入2.6.5 删除2.6.6 获取堆顶2.6.7 判空2.6.8 个数2.6.9 向上调整2.6.10 向下调整3. 堆的实现测试测试…...
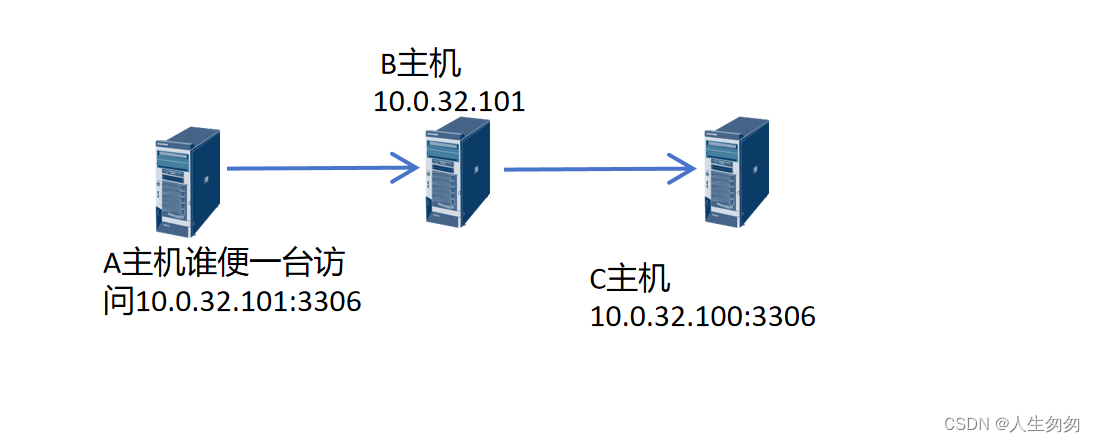
iptables配置NAT实现端口转发
加载防火墙的内核模块 modprobe ip_tables modprobe ip_nat_ftp modprobe ip_conntrack 1.开启路由转发功能 echo net.ipv4.ip_forward 1 >> /etc/sysctl.conf sysctl -p2、将本地的端口转发到本机端口 将本机的 7777 端口转发到 6666 端口。 iptables -t nat -A PR…...

【启明智显产品介绍】Model3C工业级HMI芯片详解专题(一)芯片性能
【启明智显产品介绍】工业级HMI芯片Model3C详解(一)芯片性能 Model3C 是一款基于 RISC-V 的高性能、国产自主、工业级高清显示与智能控制 MCU,配置平头哥E907,主频400MHz,强大的 2D 图形加速处理器、PNG/JPEG 解码引擎…...

Socket编程【个人简单】
介绍 Socket是计算机网络中的一种通信端点,通过它应用程序可以在网络上发送和接收数据。它可以是基于TCP(传输控制协议)的流套接字,也可以是基于UDP(用户数据报协议)的数据报套接字。 TCP、UDP、HTTP和We…...

java入门 grpc测试案例
一、 参考资料 参考孙帅suns教程 https://www.bilibili.com/video/BV13M41157gU/?p3&spm_id_from333.880.my_history.page.click&vd_source4cd1b6f268e2a29a11bea5d2568836ee 二、 服务端 项目目录 maven构建项目 pom.xml <project xmlns"http://maven.a…...
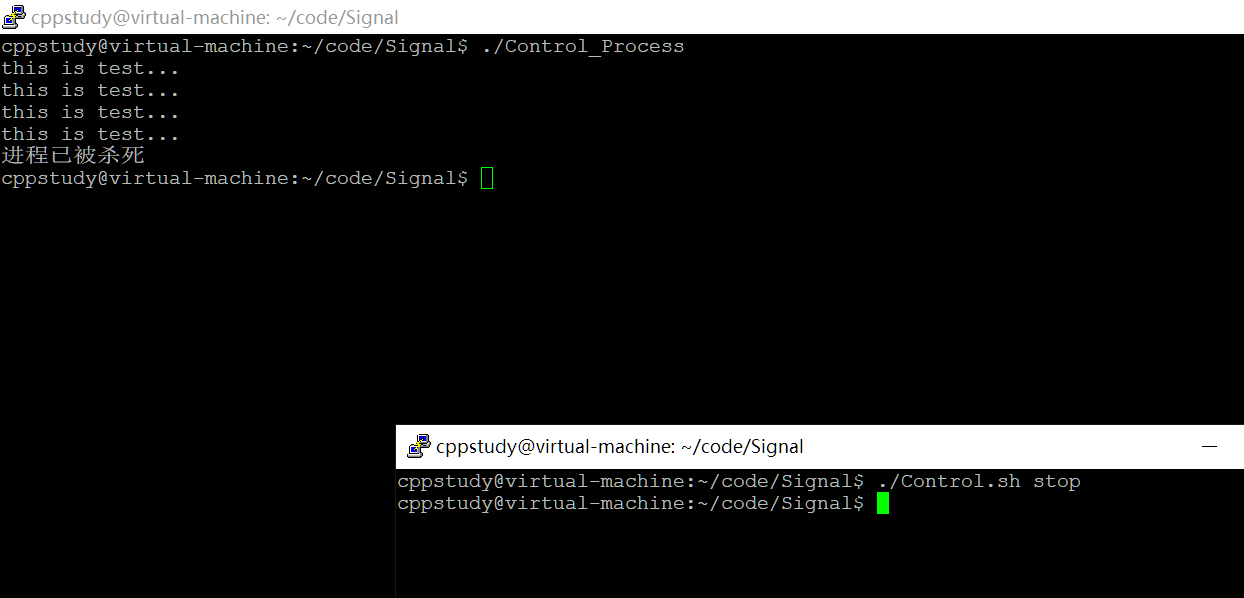
【操作系统】信号处理与阻塞函数|时序竞态问题
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 关于阻塞函数和…...
go语言day4 引入第三方依赖 整型和字符串转换 进制间转换 指针类型 浮点数类型 字符串类型
Golang依赖下载安装失败解决方法_安装go依赖超时怎么解决-CSDN博客 go安装依赖包(go get, go module)_go 安装依赖-CSDN博客 目录 go语言项目中如何使用第三方依赖:(前两步可以忽略) 一、安装git,安装程序…...

IOS Swift 从入门到精通:闭包第二部分,高级闭包
文章目录 当闭包接受参数时使用闭包作为参数当闭包返回值时使用闭包作为参数简写参数名称高级闭包: 具有多个参数的闭包高级闭包:从函数返回闭包高级闭包:捕获值总结当闭包接受参数时使用闭包作为参数 这是闭包开始变得有点像线路噪声的地方:传递给函数的闭包也可以接受它…...
爬虫超详细介绍
爬虫(Spider)是一种自动化程序,用于在互联网上获取信息。 其工作原理主要可以分为以下几个步骤: 发起请求: 爬虫首先需要向目标网站发起HTTP请求,以获取网页的内容。这个请求可以包含一些额外的信息&…...
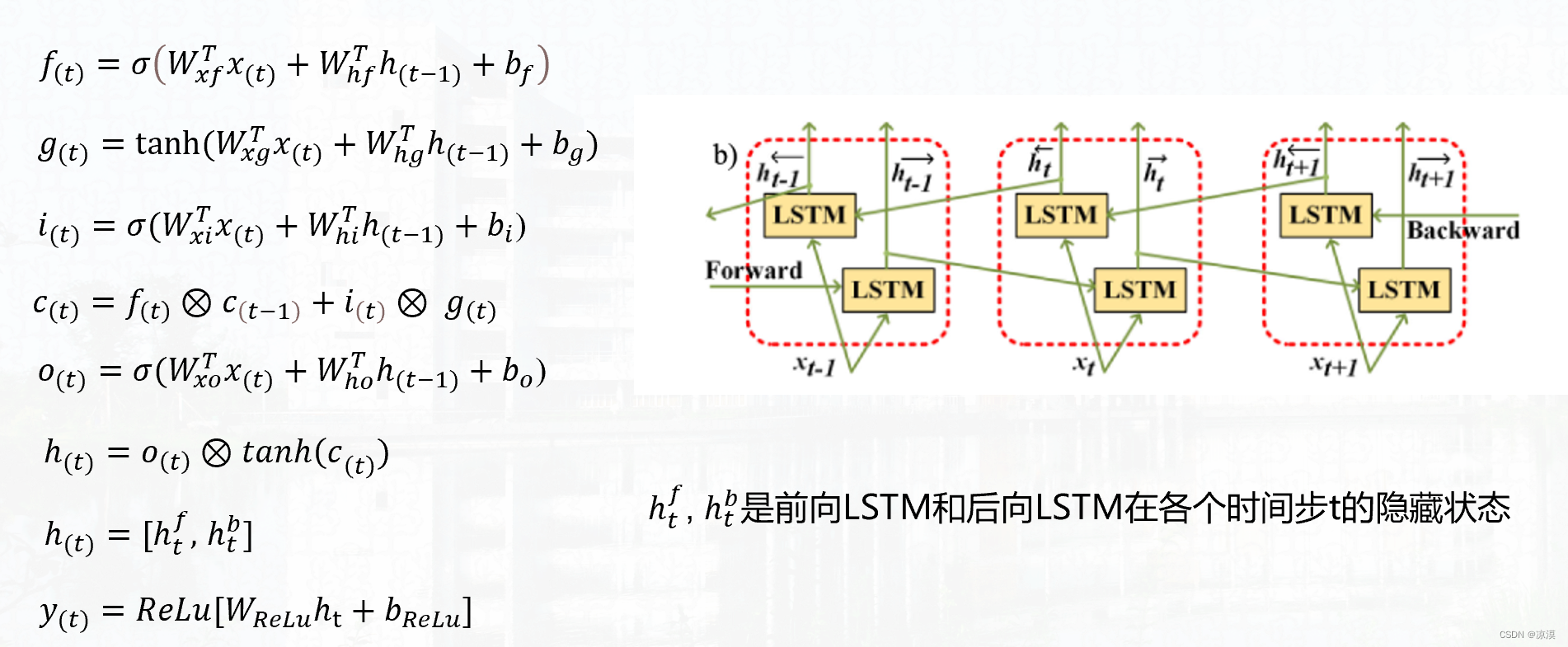
双向长短期记忆神经网络BiLSTM
先说一下LSTM LSTM 是一种特殊的 RNN,它通过引入门控机制来解决传统 RNN 的长期依赖问题。 LSTM 的结构包含以下几个关键组件: 输入门(input gate):决定当前时间步的输入信息对细胞状态的影响程度。遗忘门ÿ…...

python基础篇(4):range语句
1 功能介绍 range语句的功能是获得一个数字序列(可迭代类型的一种) 2 语法 语法1: range(num) 获取一个从0开始,到num结束的数字序列(不含num本身) 如range(5)取得的数据是:[0, 1, 2, 3, 4…...
基于STM32的简易计算器proteus仿真设计(仿真+程序+设计报告+讲解视频)
基于STM32的简易计算器proteus仿真设计 讲解视频1.主要功能2. 仿真3. 程序4. 设计报告5. 资料清单&下载链接 基于STM32的简易计算器proteus仿真设计(仿真程序设计报告讲解视频) 仿真图proteus 8.9 程序编译器:keil 5 编程语言:C语言 …...

小程序onLoad 和 onShow
onLoad 和 onShow 是小程序页面的生命周期函数,它们在不同的时机触发,具有不同的用途和执行顺序 1.onLoad: (1)onLoad 在页面加载时触发,仅执行一次。 (2)用于页面的初始化操作,例如…...

抖音直播违规规定有哪些?(直播违禁词汇总表)
全民直播的同时也有不少新手直播玩家处处碰壁,直播间没人气,直播不知道说什么甚至直播间被封。 收到直播封禁通知的朋友,轻者封禁直播账号两三天,严重着可能永久封禁直播间! 今天我们重点来说说直播间被封是怎么回事?如何避免抖音直播间被封?抖音直播间违规规定有哪些?抖音…...

安卓 jetpack compose
以下是 Jetpack Compose 中常用的一些组件的列表: 组件名称描述Text用于显示文本内容。Button可点击的按钮组件,常用于触发事件。TextField用于输入文本的文本框组件。Image用于展示图片。Column垂直布局容器,可以在其中垂直排列子组件。Row…...
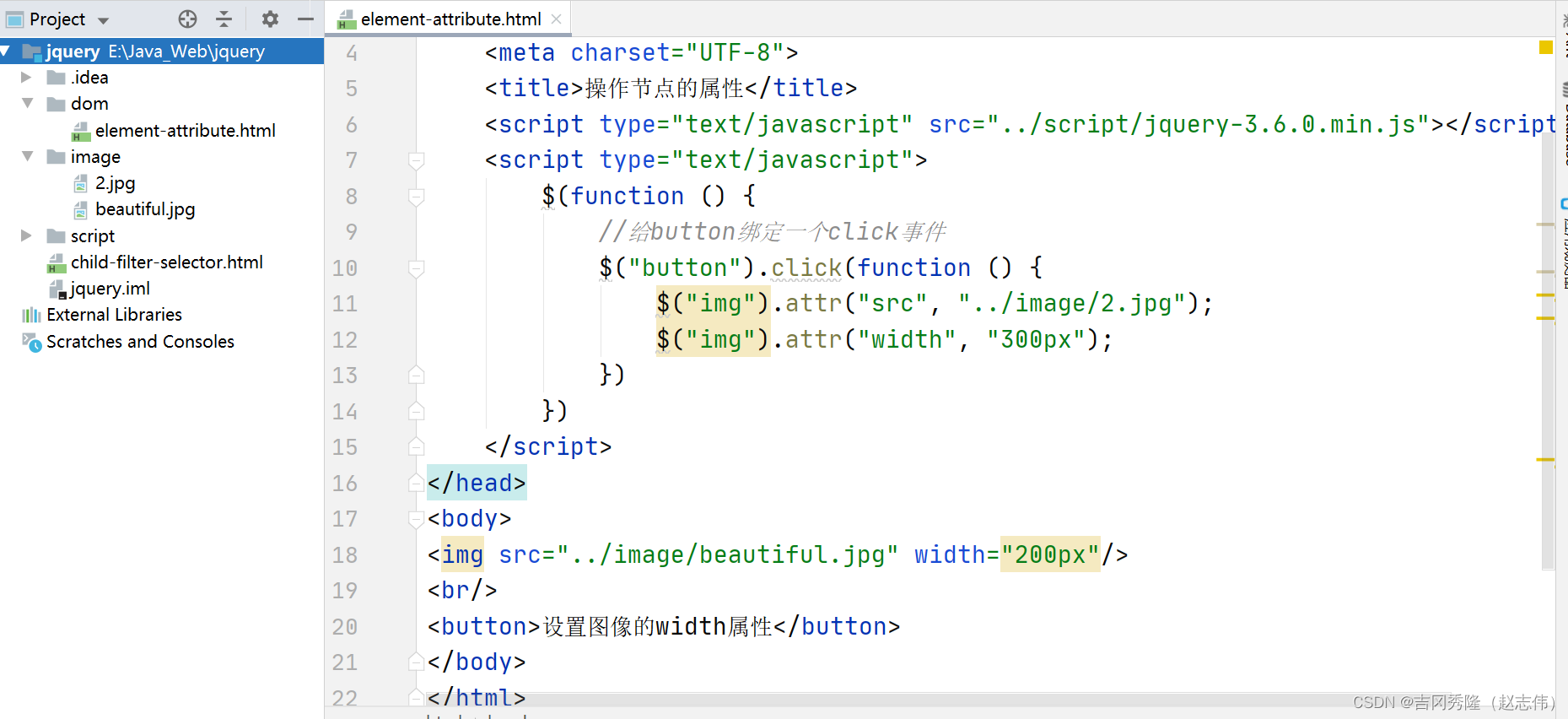
JavaWeb系列十九: jQuery的DOM操作 上
查找节点, 修改属性 查找属性节点: 查找到所需要的元素之后, 可以调用jQuery对象的attr()方法用来 设置/返回 它的各种属性值 设置属性值 $(“img”).attr(“width”, “300”);返回属性值 $(“img”).attr(“width”); 创建节点 创建节点: 使用jQuery的工厂函数$(): $(html标…...
JavaWeb系列十一: Web 开发会话技术(Cookie, Session)
韩sir Cookie技术Cookie简单示意图Cookie常用方法Cookie创建Cookie读取JSESSIONID读取指定Cookie Cookie修改Cookie生命周期Cookie的有效路径Cookie作业布置Cookie注意事项Cookie中文乱码问题 Session技术Session原理示意图Session常用方法Session底层机制Session生命周期Sessi…...
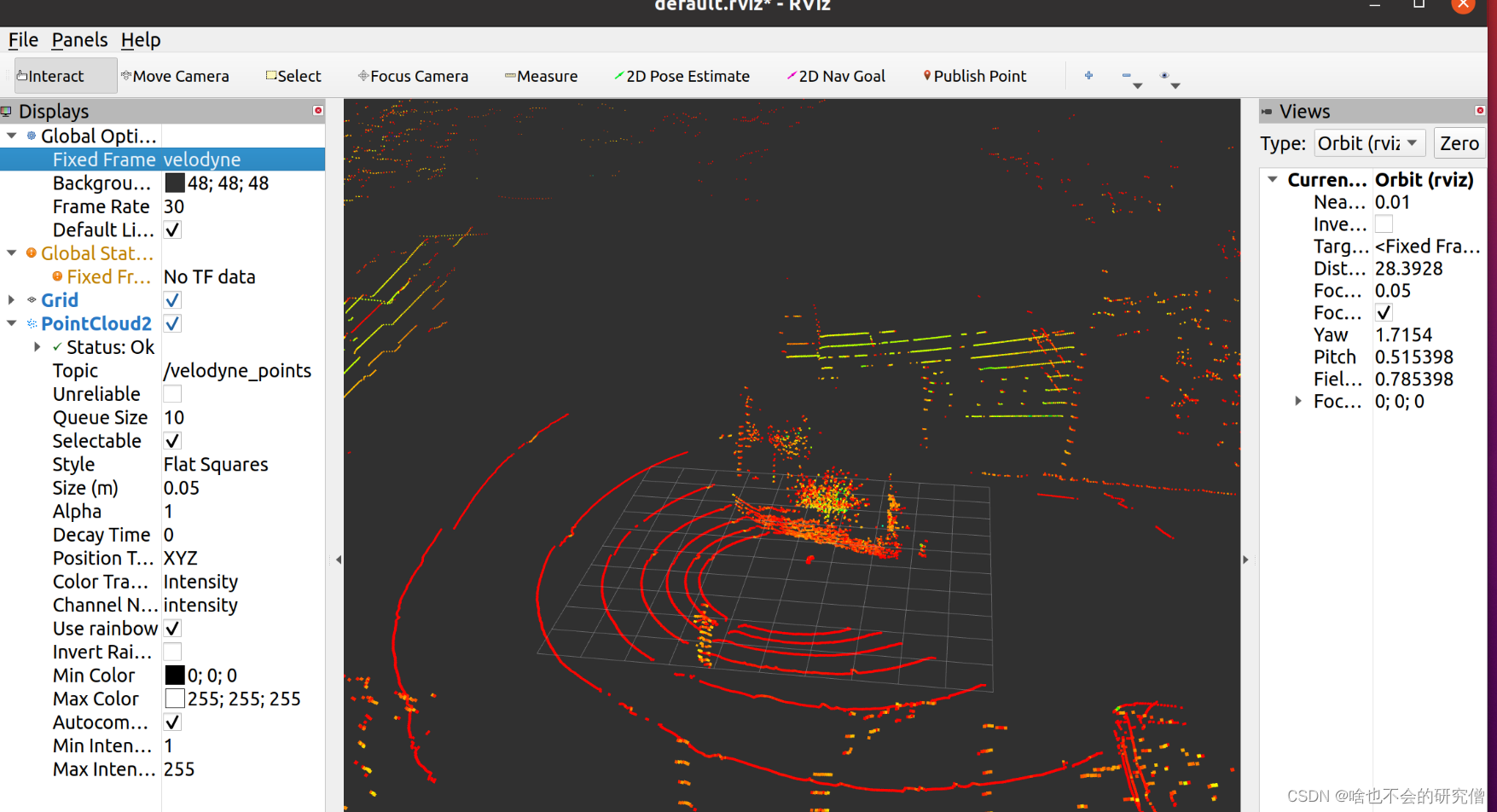
【激光雷达使用记录】—— 如何在ubuntu中利用ros自带的rviz工具实时可视化雷达点云的数据
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、查看雷达数据的 frame_id1. 查看雷达数据的话题2. 查看数据的frame_id 二、可视化雷达数据总结 前言 RViz(ROS Visualization)是机…...
一道session文件包含题
目录 环境说明 session文件包含getshell 审计源码 session包含 base64在session中的解码分析 题目: 链接:https://pan.baidu.com/s/1Q0BN08b8gWiVE4tOnirpTA?pwdcate 提取码:cate 环境说明 这里我用的是linux,也可以用p…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...