【前后端实现】AHP权重计算
AHP权重计算:
需求:前端记录矩阵维度、上三角值,后端构建比较矩阵、计算权重值并将结果返回给前端
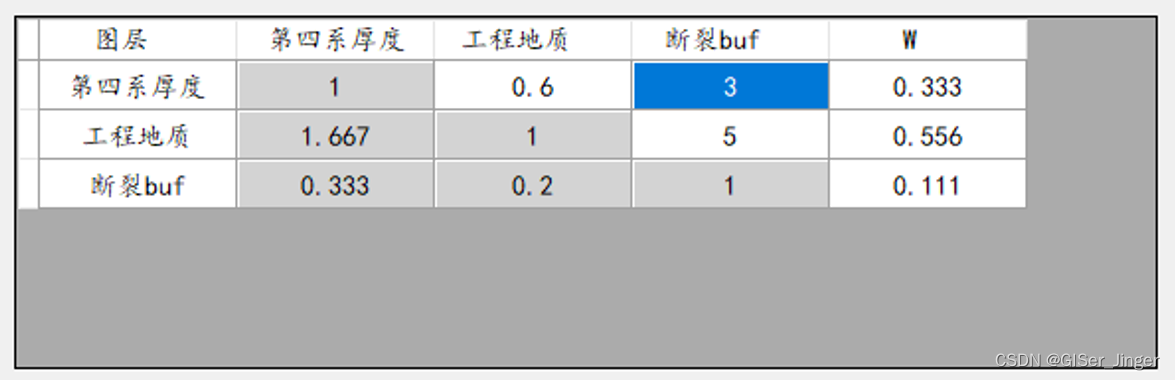
比较矩阵构建
如果你想要根据上三角(不包括对角线)的值来构建对称矩阵,那么你可以稍作修改上述的
generate_symmetric_matrix函数。在这个情况下,你将从矩阵的左上角开始填充上三角的值,然后利用对称性填充下三角的值。
def generate_symmetric_matrix_from_upper(i, upper_triangle_values): """ 根据上三角(不包括对角线)的值和矩阵维度生成对称矩阵 :param i: 矩阵的维度(i x i) :param upper_triangle_values: 上三角(不包括对角线)的值列表 :return: 生成的对称矩阵 """ if len(upper_triangle_values) > i * (i - 1) // 2: raise ValueError("提供的上三角值数量超过了上三角(不包括对角线)的元素总数。") # 初始化矩阵 matrix = [[1] * i for _ in range(i)] # 对角线初始化为1 # 填充上三角(不包括对角线)的值 index = 0 for row in range(i): for col in range(row + 1, i): # 从当前行的下一个元素开始(跳过对角线) matrix[row][col] = upper_triangle_values[index] index += 1 # 填充下三角的值(利用对称性) for row in range(i): for col in range(row): # 只遍历到当前行的前一个元素(不包括对角线) matrix[row][col] = 1/matrix[col][row] # 下三角的值等于上三角的值 return matrix # 示例使用
i = 3 # 矩阵维度
upper_triangle_values = [0.6, 3, 5] # 上三角(不包括对角线)的值
matrix = generate_symmetric_matrix_from_upper(i, upper_triangle_values) # 打印矩阵
for row in matrix: print(row)
- 在这个函数中,我们首先检查提供的上三角值的数量是否超过了实际需要的数量。然后,我们初始化一个所有对角线元素都为1的矩阵。接着,我们遍历上三角(不包括对角线)并填充提供的值。最后,我们利用对称性来填充下三角的值。
- 当你运行这个示例时,它将输出一个3x3的对称矩阵,其中上三角的值由
upper_triangle_values列表提供,而下三角的值则通过对称性从上三角复制而来。对角线上的值保持为1。
AHP权重计算
层次分析法(Analytic Hierarchy Process, AHP)是一种常用的多属性决策方法,它允许决策者将复杂的决策问题分解为多个子问题或属性,并通过两两比较的方式来确定这些子问题或属性的相对重要性。以下是一个简化的Python示例,展示了如何使用层次分析法求解权重值:
- 构造判断矩阵(通过专家打分等方式)
- 一致性检验
- 求解权重值
import numpy as np def calculate_consistency_ratio(ci, n): # 一致性指标RI的值与n(判断矩阵的阶数)有关 ri_values = { 1: 0.0, 2: 0.0, 3: 0.58, 4: 0.9, 5: 1.12, 6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45, 10: 1.49 } ri = ri_values[n] cr = ci / ri return cr def calculate_ci(matrix): # 计算一致性指标CI n = matrix.shape[0] eigenvalues, _ = np.linalg.eig(matrix) max_eigenvalue = np.max(eigenvalues) ci = (max_eigenvalue - n) / (n - 1) return ci def calculate_weights(matrix): # 计算权重值 eigenvalues, eigenvectors = np.linalg.eig(matrix) max_eigenvalue = np.max(eigenvalues) max_eigenvector = eigenvectors[:, eigenvalues == max_eigenvalue] weights = max_eigenvector.flatten().real / np.sum(max_eigenvector.flatten().real) return weights def ahp_analysis(matrix): # AHP分析主函数 n = matrix.shape[0] ci = calculate_ci(matrix) cr = calculate_consistency_ratio(ci, n) if cr < 0.1: # 一般情况下,当CR<0.1时,认为判断矩阵的一致性是可以接受的 weights = calculate_weights(matrix) print("一致性检验通过,权重值为:", weights) else: print("一致性检验未通过,需要重新调整判断矩阵") # 示例判断矩阵(假设) # 注意:这里的判断矩阵应该是通过专家打分或其他方式构造的,并且应该满足互反性 A = np.array([ [1, 3, 5], [1/3, 1, 3], [1/5, 1/3, 1] ]) ahp_analysis(A)注意:
- 上述代码中的判断矩阵
A是假设的,实际应用中需要根据实际情况构造。- 一致性检验的阈值通常是0.1,但也可以根据具体需求进行调整。
- 判断矩阵的构造应该遵循AHP方法的规则,即对角线元素为1,且满足互反性(即
A[i][j] = 1 / A[j][i])。- 权重值是通过求解判断矩阵的最大特征值对应的特征向量得到的,并且需要对该特征向量进行归一化处理。
前后端设计
在前后端通信中,当前端需要传递两个参数给后端,其中一个参数是数组,另一个是int类型时,你需要在前端正确地构造请求,并在后端Flask应用中设计相应的路由和请求处理函数来接收这些参数。
前端(JavaScript 使用 fetch API)
假设你正在使用JavaScript的fetch API来发送POST请求,你可以将数组和int值作为JSON对象的一部分发送。这里是一个例子:
// 假设你的后端API的URL是'http://example.com/api/data'
const arrayParam = [1, 2, 3]; // 数组参数
const intParam = 42; // int类型参数 // 将参数包装在一个对象中
const dataToSend = { arrayParam: arrayParam, intParam: intParam
}; // 将对象转换为JSON字符串
const jsonData = JSON.stringify(dataToSend); fetch('http://example.com/api/data', { method: 'POST', headers: { 'Content-Type': 'application/json' }, body: jsonData
})
.then(response => response.json())
.then(data => console.log(data))
.catch((error) => { console.error('Error:', error);
});后端(Flask)
在后端,你需要在Flask应用中创建一个路由,并使用request.json来获取前端发送的JSON数据。这里是一个例子:
from flask import Flask, request, jsonify app = Flask(__name__) @app.route('/api/data', methods=['POST'])
def receive_data(): if request.method == 'POST': # 从JSON中解析参数 array_param = request.json.get('arrayParam', []) # 默认值为空数组 int_param = request.json.get('intParam', None) # 默认值为None,你可以根据需要设置默认值 # 检查int_param是否为int类型 if int_param is not None and not isinstance(int_param, int): return jsonify({'error': 'intParam must be an integer'}), 400 # 在这里处理你的数据... # 例如,你可以返回接收到的参数作为确认 return jsonify({'message': 'Data received!', 'arrayParam': array_param, 'intParam': int_param}), 200 else: return jsonify({'error': 'Invalid request method'}), 405 if __name__ == '__main__': app.run(debug=True)在这个例子中,
receive_data函数首先检查请求方法是否为POST。然后,它从request.json中获取arrayParam和intParam。注意,我使用了get方法来安全地获取这些值,并为它们提供了默认值(对于arrayParam是一个空数组,对于intParam是None)。然后,它检查intParam是否是一个整数,如果不是,则返回一个错误响应。最后,它返回一个包含接收到的参数的JSON响应。
postman测试:
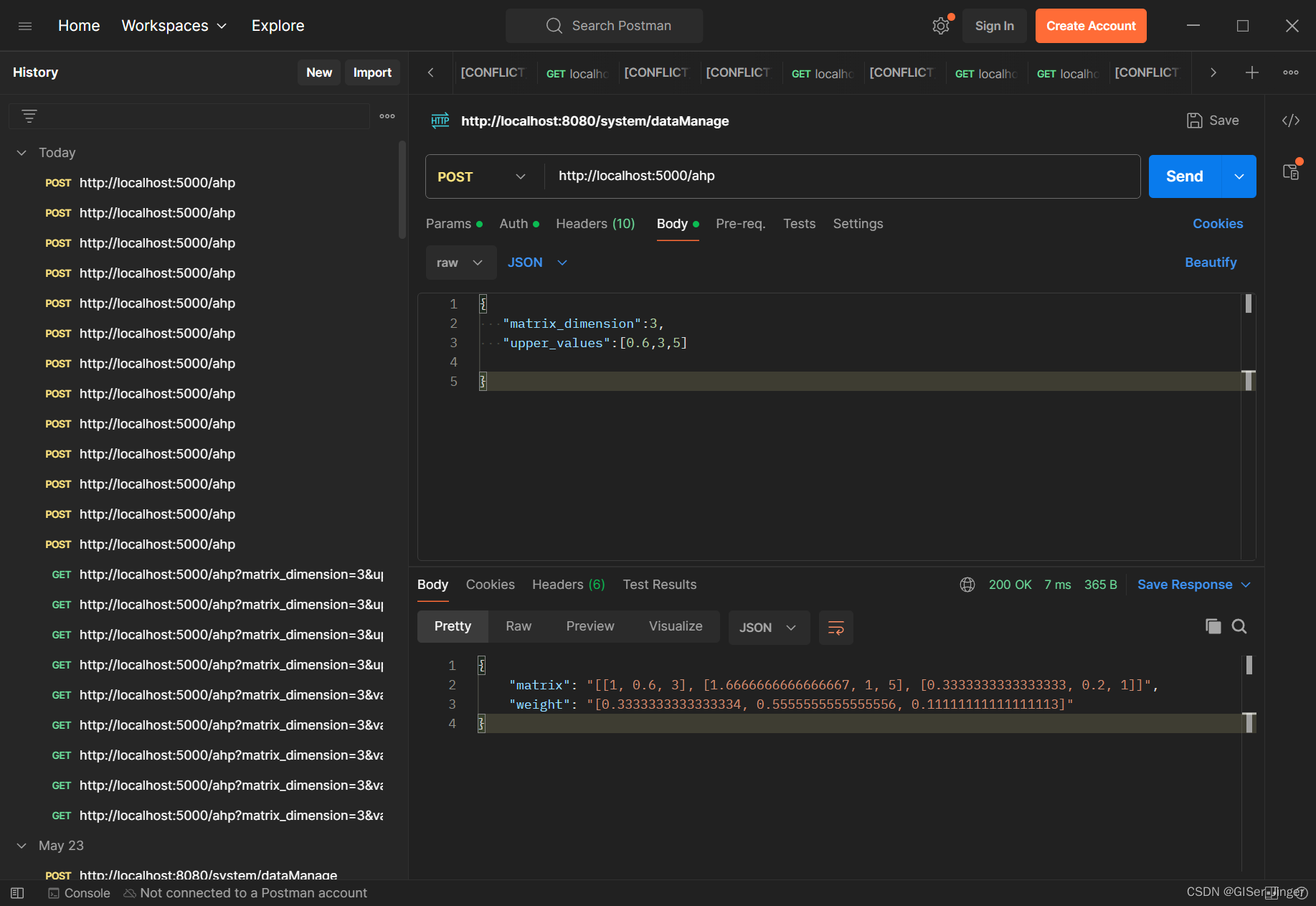
后端模块与接口 :
AHP.py
import jsonimport numpy as npdef calculate_consistency_ratio(ci, n):# 一致性指标RI的值与n(判断矩阵的阶数)有关ri_values = {1: 0.0, 2: 0.0, 3: 0.58, 4: 0.9, 5: 1.12,6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45, 10: 1.49}ri = ri_values[n]cr = ci / rireturn crdef calculate_ci(matrix):# 计算一致性指标CIn = matrix.shape[0]eigenvalues, _ = np.linalg.eig(matrix)max_eigenvalue = np.max(eigenvalues)ci = (max_eigenvalue - n) / (n - 1)return cidef calculate_weights(matrix):# 计算权重值eigenvalues, eigenvectors = np.linalg.eig(matrix)max_eigenvalue = np.max(eigenvalues)max_eigenvector = eigenvectors[:, eigenvalues == max_eigenvalue]weights = max_eigenvector.flatten().real / np.sum(max_eigenvector.flatten().real)return weightsdef ahp_analysis(matrix):# AHP分析主函数n = matrix.shape[0]ci = calculate_ci(matrix)cr = calculate_consistency_ratio(ci, n)if cr < 0.1: # 一般情况下,当CR<0.1时,认为判断矩阵的一致性是可以接受的weights = calculate_weights(matrix)print("一致性检验通过,权重值为:", weights)else:print("一致性检验未通过,需要重新调整判断矩阵")return weightsdef generate_symmetric_matrix_from_upper(i, upper_triangle_values):"""根据上三角(不包括对角线)的值和矩阵维度生成对称矩阵:param i: 矩阵的维度(i x i):param upper_triangle_values: 上三角(不包括对角线)的值列表:return: 生成的对称矩阵"""if len(upper_triangle_values) != i * (i - 1) / 2:raise ValueError("提供的上三角值数量不匹配。")# 初始化矩阵matrix = [[1] * i for _ in range(i)] # 对角线初始化为1# 填充上三角(不包括对角线)的值index = 0for row in range(i):for col in range(row + 1, i): # 从当前行的下一个元素开始(跳过对角线)matrix[row][col] = upper_triangle_values[index]index += 1# 填充下三角的值(利用对称性)for row in range(i):for col in range(row): # 只遍历到当前行的前一个元素(不包括对角线)matrix[row][col] = 1/matrix[col][row] # 下三角的值等于上三角的值return matrix# 方法,前端传来矩阵维数+上三角值【row1Value1,row1Value2,row2Value2】数组,自动生成矩阵并返回AHP分析结果值
def cal_AHP_res(matrixDimension,upper_triangle_values):matrix = generate_symmetric_matrix_from_upper(matrixDimension,upper_triangle_values)A = np.array(matrix)matrix_res=json.dumps(matrix)arr= ahp_analysis(A)# 将其转换为 Python 列表list_arr = arr.tolist()# 将列表转换为 JSON 字符串res = json.dumps(list_arr)return matrix_res,resif __name__ == '__main__':# 生成矩阵示例i = 3 # 矩阵维度upper_triangle_values = [3, 0.75, 0.5] # 上三角(不包括对角线)的值matrix_res, res=cal_AHP_res(i,upper_triangle_values)//flask接口
@app.route('/ahp', methods=['POST'])
def getAHPRes():matrix_dimension=request.json.get('matrix_dimension')value = request.json.get('upper_values',[]) # 获取数值型值 valuesprint(len(value))matrix,weight= cal_AHP_res(matrix_dimension,value)return jsonify({'matrix': matrix,'weight':weight})相关文章:

【前后端实现】AHP权重计算
AHP权重计算: 需求:前端记录矩阵维度、上三角值,后端构建比较矩阵、计算权重值并将结果返回给前端 比较矩阵构建 如果你想要根据上三角(不包括对角线)的值来构建对称矩阵,那么你可以稍作修改上述的generate…...

K8S日常运维手册
Kubernetes(简称 K8S)是一种广泛使用的容器编排平台,能够自动化部署、扩展和管理容器化应用。对于运维人员来说,掌握 Kubernetes 的日常运维技能是确保系统稳定运行的关键。本文将介绍一些 Kubernetes 日常运维的基本操作与技巧&a…...
现在的Java面试都这么扯淡了吗?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「java的资料从专业入门到高级教程」, 点个关注在评论区回复“666”之后私信回复“666”,全部无偿共享给大家!!!开发兼过半年面试官 刚开始…...

安全加固 MariaDB 和 MySQL 数据库
安全加固 MariaDB 和 MySQL 数据库 在今天的网络环境中,保护数据库安全至关重要,特别是像 MariaDB 和 MySQL 这样的流行数据库。本文将介绍一些关键的安全加固步骤,以确保数据库系统的安全性和稳定性。 1. 数据库版本和基础设置 首先&…...
【计算机毕业设计】167校园失物招领微信小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

yum的概念、相关命令、ftp http部署步骤;NFS共享文件操作步骤
目录 yum 配置文件 缓存功能操作步骤 创建并配置本地仓库文件 yum相关命令 yum install __ yum repolist yum list __ yum info __ yum search __ yum whatprovides __ yum remove __ yum -y update __ yum history yum grouplist yum groupinstall "__&q…...
Spire.PDF for .NET【文档操作】演示:如何删除 PDF 中的图层
借助Spire.PDF,我们可以在新建或现有pdf文档的任意页面中添加线条、图像、字符串、椭圆、矩形、饼图等多种图层。同时,它还支持我们从pdf文档中删除特定图层。 Spire.PDF for .NET 是一款独立 PDF 控件,用于 .NET 程序中创建、编辑和操作 PD…...
【c语言】二级指针
1,定义 本质还是从指针的角度去理解,只不过存的指针的值 2,使用方法...

心理健康测试系统设计
心理健康测试系统设计需要综合考虑多个方面,以确保系统的准确性、易用性和有效性。以下是一个心理健康测试系统设计方案: 一、设计目标 准确性:确保测试结果能够准确反映被测者的心理健康状况。 易用性:设计简洁明了的界面和操作…...

webcomponents学习
一、新建index.html文件 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Document</title>…...
2024会展行业发展趋势预测
在当今这个数字化浪潮汹涌的时代,会展行业也迎来了自己的变革时刻。 根据《2023中国会展主办机构数字化调研报告》,我们可以清晰地看到几个显著的趋势: 首先,数字化转型已经不再是一道选择题,而是必答题。 超过90%的…...
达梦(DM8)数据库备份与还原(逻辑备份)二
一、达梦数据库的逻辑备份分四种级别的导出(dexp)与导入(dimp)的备份 第一种是:数据库级:导出或导入数据库中所有的对象。主要参数是:FULL 第二种是:用户级别:导出或导…...
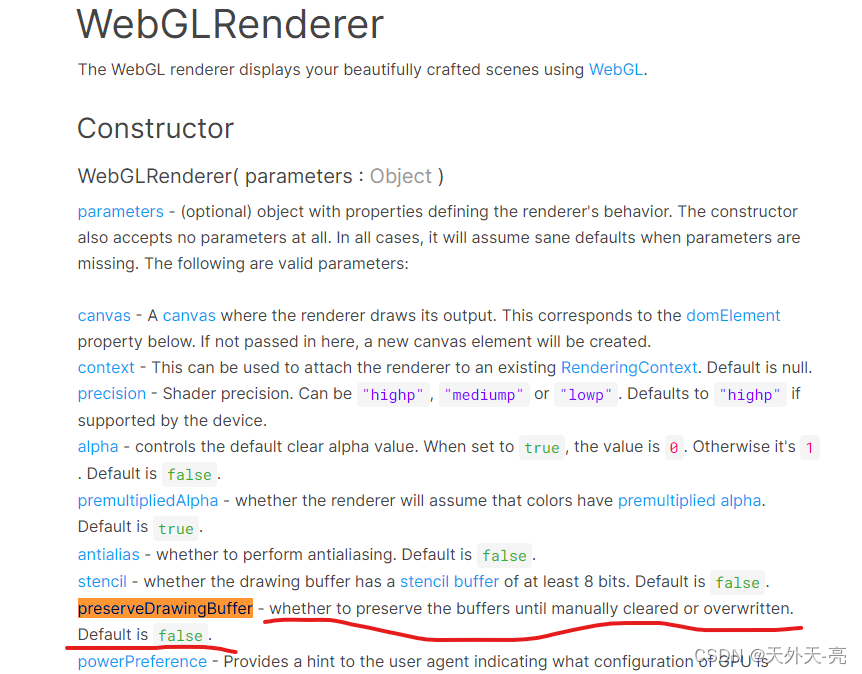
ThreeJS-截屏下载pdf或者图片时白屏
JS-页面截图下载为pdf 关于如何下载为 pdf 在上面的这篇文章中有写,大家可以看下,下载图片代码在最下面 这时我们发现 three 部分是空白的如下: 这就多少有点尴尬了,这时我们习惯性的看下后台报错 是不是发现了惊喜,…...

redis以后台的方式启动
文章目录 1、查看redis安装的目录2、Redis以后台的方式启动3、通过客户端连接redis4、连接后,测试与redis的连通性 1、查看redis安装的目录 [rootlocalhost ~]# cd /usr/local/redis/ [rootlocalhost redis]# ll 总用量 112 drwxr-xr-x. 2 root root 150 12月 6…...

力扣随机一题 哈希表 排序 数组
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 2491.划分技能点相等的团队【中等】 题目: 给你一个正整数数组…...
昇思25天学习打卡营第01天|基本介绍
作为曾经的javaer,本着不断学习的初心,报名了昇思25天的课程,希望自己能学会点东西的目的。 昇思MindSpore介绍 昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景统一部署三大目标。 其中,…...

问题:1、金属基复合材料界面的物理结合是指 #学习方法#媒体
问题:1、金属基复合材料界面的物理结合是指 A.与化学作用有关,既有化学键力存在,又有范德华力存在 B.是一种纯的物理作用,与化学作用无关,即无化学键力存在,但有范德华力存在 C&a…...

突发!OpenAI停止不支持国家API,7月9日开始执行
6月25日凌晨,有部分开发者收到了OpenAI的信,“根据数据显示,你的组织有来自OpenAl目前不支持的地区的API流量。从7月9日起,将采取额外措施,停止来自不在OpenAI支持的国家、地区名单上的API使用。” 但这位网友表示&am…...

大数据集群数据传输
简单的服务器间的通信示例 netcat,简写为 nc,是 unix 系统下一个强大的命令行网络通信工具,用于在两台主机之间建立 TCP 或者 UDP 连接,并提供丰富的命令进行数据通信。nc 在网络参考模型属于应用层。使用 nc 可以做很多事情&…...

css-vxe列表中ant进度条与百分比
1.vxe列表 ant进度条 <vxe-column field"actualProgress" title"进度" align"center" width"200"><template #default"{ row }"><a-progress:percent"Math.floor(row.actualProgress)"size"s…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
