蓝桥杯嵌入式ADC与DAC(都不需要中断)
目录
1.原理图
(1)ADC的原理图
(2)DAC的原理图
2.STM32CubeMX的配置
(1)ADC的配置
(2)DAC配置
3.代码部分
(1)ADC代码
(2)DAC代码
1.原理图
(1)ADC的原理图

作用:将模拟信号转换为数字信号
转换的方法:逐次逼近型,将片内模拟量和一个数字量对应的模拟量比较,得到最接近的值
蓝桥杯嵌入式板子上有两个12位的ADC转换器,每一个ADC具有19个多路复用通道,结果存储在16位寄存器中 (因此16位多4位存在左对齐还是右对齐,DAC也是)
个人理解是STM32G431RBT6这个芯片可以处理这个信号,将它转换?(希望有人能告诉我这个转换是从哪里完成的,谢谢!)
(2)DAC的原理图 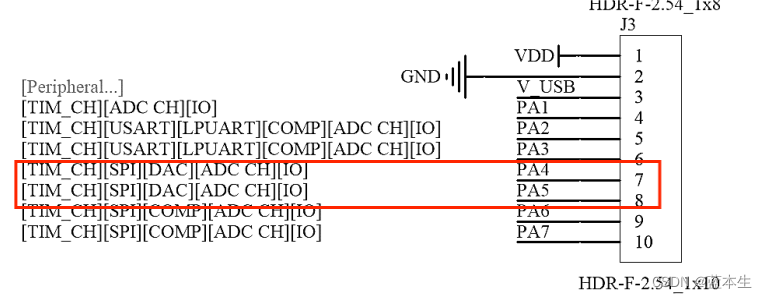
作用:将数字信号转换成模拟信号
转换的方法:电流型DAC
蓝桥杯嵌入式板子的DAC模块是12位电压输出模数转换器,可配置为8或12位,两路输出通道
2.STM32CubeMX的配置
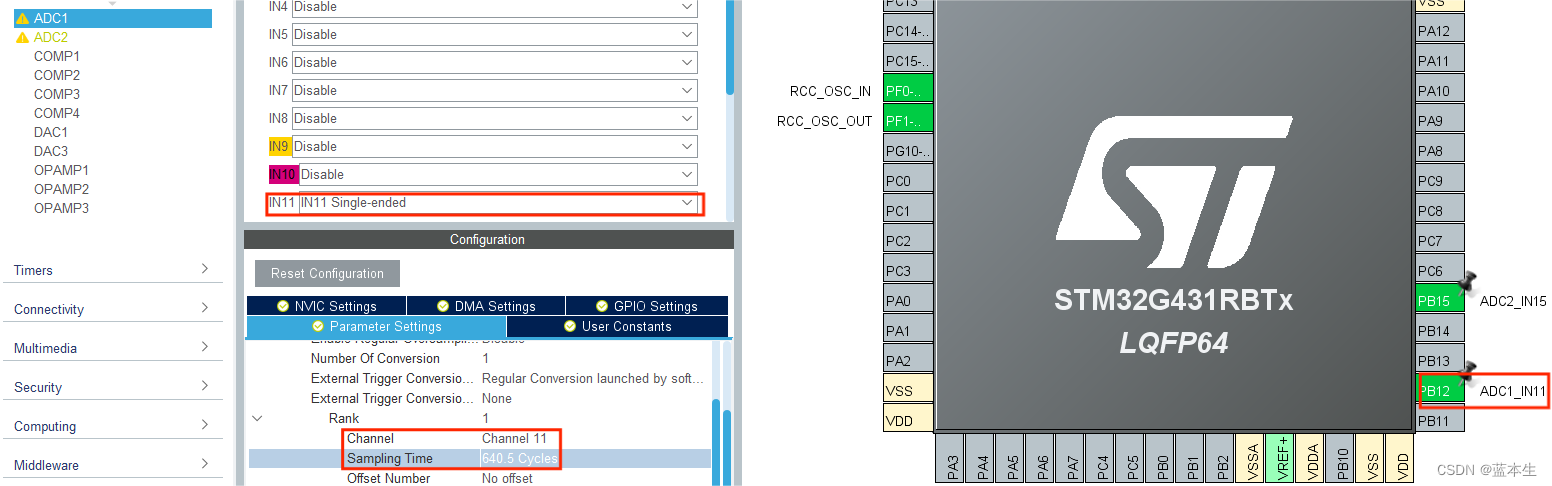
(1)ADC的配置
转换周期越短,精度越低,转换时间越长精度愈高
ADC转换时间计算公式为(转换周期+12.5(精度+0.5))*时钟周期
(2)DAC配置
连接到外部的引脚,不要连接到内部

3.代码部分
(1)ADC代码
关键函数:
HAL_ADC_Start(ADC_HandTypeDef *hadc)//开始转换
HAL_ADC_PollForConversion(ADC_HandTypedef *hadc,uint8_t Timeout)//等待完成
HAL_ADC_GetValue(ADC_HandTypedef *hadc)//获得转换结果
HAL_ADC_Stop(ADC_HandTypedef *hadc)//停止转换代码的作用是获取当前值,按照需要再展示
int R37=0,R38=0;
void get_adcvalue(void)
{HAL_ADC_Start(&hadc1);HAL_ADC_PollForConversion(&hadc1,10);R38 = HAL_ADC_GetValue(&hadc1);HAL_ADC_Stop(&hadc1);HAL_ADC_Start(&hadc2);HAL_ADC_PollForConversion(&hadc2,10);R37 = HAL_ADC_GetValue(&hadc2);HAL_ADC_Stop(&hadc2);
}(2)DAC代码
关键函数
HAL_DAC_Start(DAC_HandTypeDef *hdac,uint8_t Channel)//开始通道转换,指定通道
HAL_DAC_SetValue(DAC_HandTypeDef *hdac,uint32_t Channel,uint32_t Alignment,uint32_t Dta)
HAL_DAC_Stop(DAC_HandTypeDef *hdac,uint32_t Channel)//停止转换
关键函数代码
void set_dacvalue(float value1,float value2)
{int temp1 = (value1/3.3)*4096;HAL_DAC_SetValue(&hdac1,DAC_CHANNEL_1,DAC_ALIGN_12B_R,temp1);int temp2 = (value2/3.3)*4096;HAL_DAC_SetValue(&hdac1,DAC_CHANNEL_2,DAC_ALIGN_12B_R,temp2);
}相关文章:

蓝桥杯嵌入式ADC与DAC(都不需要中断)
目录 1.原理图 (1)ADC的原理图 (2)DAC的原理图 2.STM32CubeMX的配置 (1)ADC的配置 (2)DAC配置 3.代码部分 (1)ADC代码 (2)DA…...

网络视频的防盗与破解
网络视频(Web 视频)是指利用 HTML5 技术在浏览器中播放的视频,这类视频资源通常可以被随意下载,某些行业(比如教培行业)如果希望保护自己的视频资源不被下载,就需要对视频做防盗链处理。 防盗链需要着重加强两个方面的安全性:网络传输和客户端。 网络传输安全 网络传…...
FPGA 20个例程篇:20.USB2.0/RS232/LAN控制并行DAC输出任意频率正弦波、梯形波、三角波、方波(二)
通过上面的介绍相信大家对数字变频已经有了一个较为整体性的认识,下面笔者来对照XILINX的DDS IP核对数字变频技术展开更进一步的说明,做到了理论和实践很好地结合,这样大家再带入Modelsim进行仿真测试就不仅掌握了数字变频的理论知识…...

接口中新增方法,接口应用和适配器设计模式
目录 JDK8以后接口中新增方法 接口中默认方法注意事项: 新增方法static 接口中静态方法的注意事项: JDK9新增的方法 JDK8以后接口中新增方法 允许在接口中定义默认的方法,需要使用关键字default修饰作用:解决接口升级的问题 …...
自主HttpServer实现(C++实战项目)
文章目录项目介绍CGI技术概念原理设计框架日志文件TCPServer任务类初始化与启动HttpServerHTTP请求结构HTTP响应结构线程回调EndPoint类EndPoint主体框架读取HTTP请求处理HTTP请求CGI处理非CGI处理构建HTTP响应发送HTTP响应接入线程池简单测试项目扩展项目介绍 该项目是一个基…...

第26篇:Java数组API总结
目录 1、数组基本概念 2、Java如何声明数组 2.1中括号在数据类型之前 2.2 中括号在数据类型之后...

[C++] 信号
前言 信号与槽是QT的一个概念,原版C里并没有 使用 先声明一些类 Receiver负责接收信号,Emitter2则是负责发送 class Receiver : public ntl::Reflectible { public:void received(int num){std::cout << "received:" << num &…...
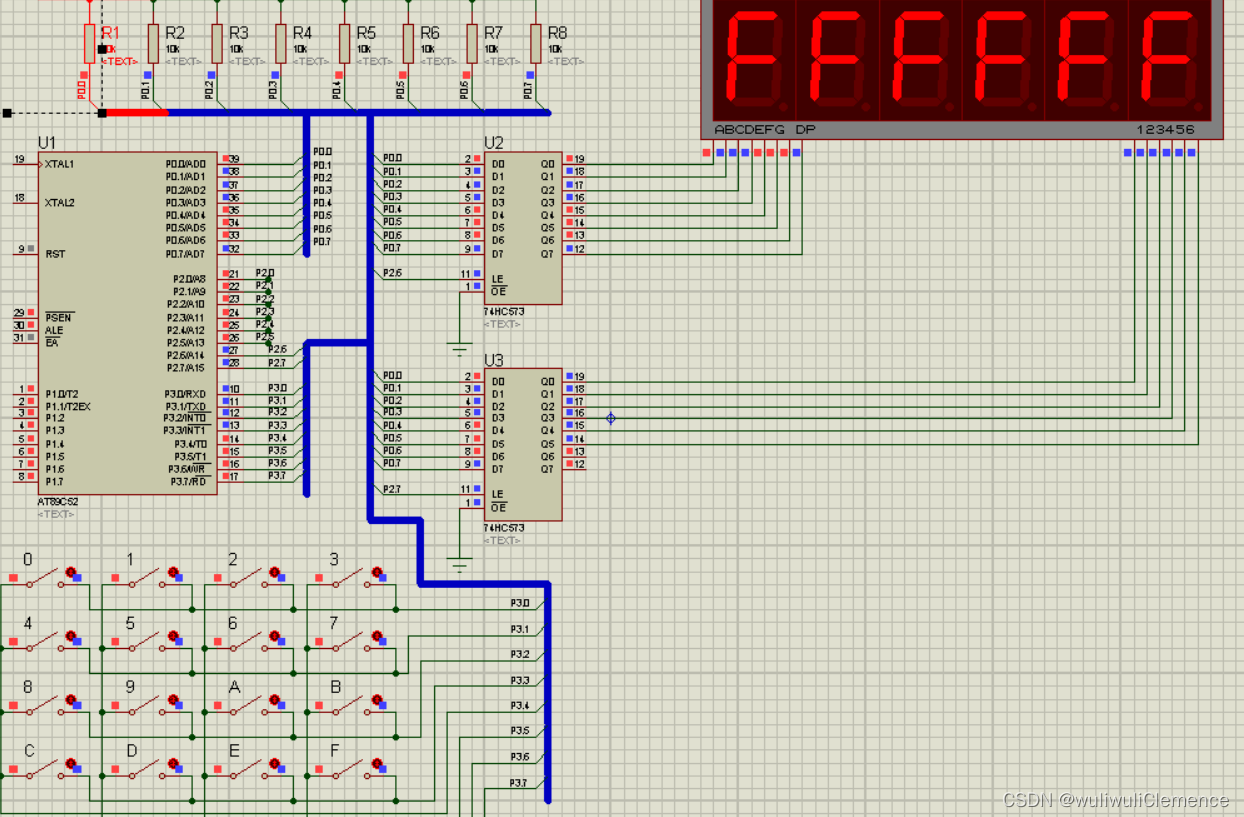
单片机——矩阵按键模块
主要目的 学会按键扫描 1.延时函数 延时函数部分详见链接: 单片机控制一盏灯的亮与灭程序解释 void delay (uint k) //定义延时函数{uint i,j;for(i<0;i<k;i){for(j0;j<113;j){;}}}这个程序里面的延时函数的目的是按键消抖。 2.按键扫描模块 这是本次实验的重点&a…...

Android学习之网络操作
网络操作 Android平台下的原生网络操作可以分为以下几步: 创建URL对象;通过URL对象获取HttpURLConnection对象;通过HttpURLConnection对象设置请求头键值对、网络连接超时时间等;通过HttpURLConnection对象的connect()方法建立网…...

Delphi XE开发android开发环境搭建
Delphi xe为使用Delphi作为开发工具的程序员,提供了开发APP的便捷工具,它的开发环境也是非常容易搭建,这里我简述一下Android的开发环境搭建,Delphi XE开发Android程序的开发环境需要三个软件支持:Java SE Development开发环境、Android SDK和Android Ndk开发环境。 1、安…...
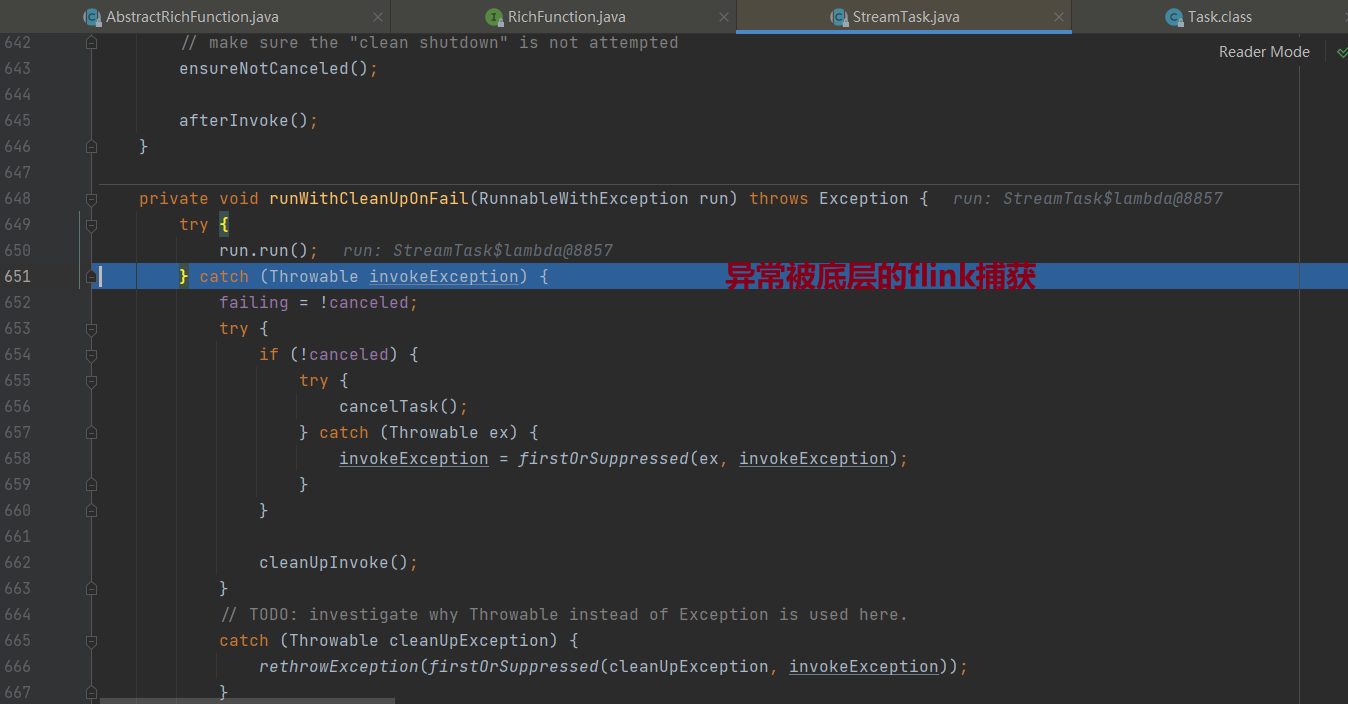
flink入门-流处理
入门需要掌握:从入门demo理解、flink 系统架构(看几个关键组件)、安装、使用flink的命令跑jar包flink的webUI 界面的监控、常见错误、调优 一、入门demo:统计单词个数 0、单词txt 文本内容(words.txt): hello world …...

【数据结构】单链表中,如何实现 将链表中所有结点的链接方向“原地”逆转
一.实现一个单链表(无头单向不循环) 我们首先实现一个无头单向不循环单链表。 写出基本的增删查改功能,以及其它的一些功能(可忽略)。 #include<stdio.h> #include<assert.h> #include<stdlib.h>…...
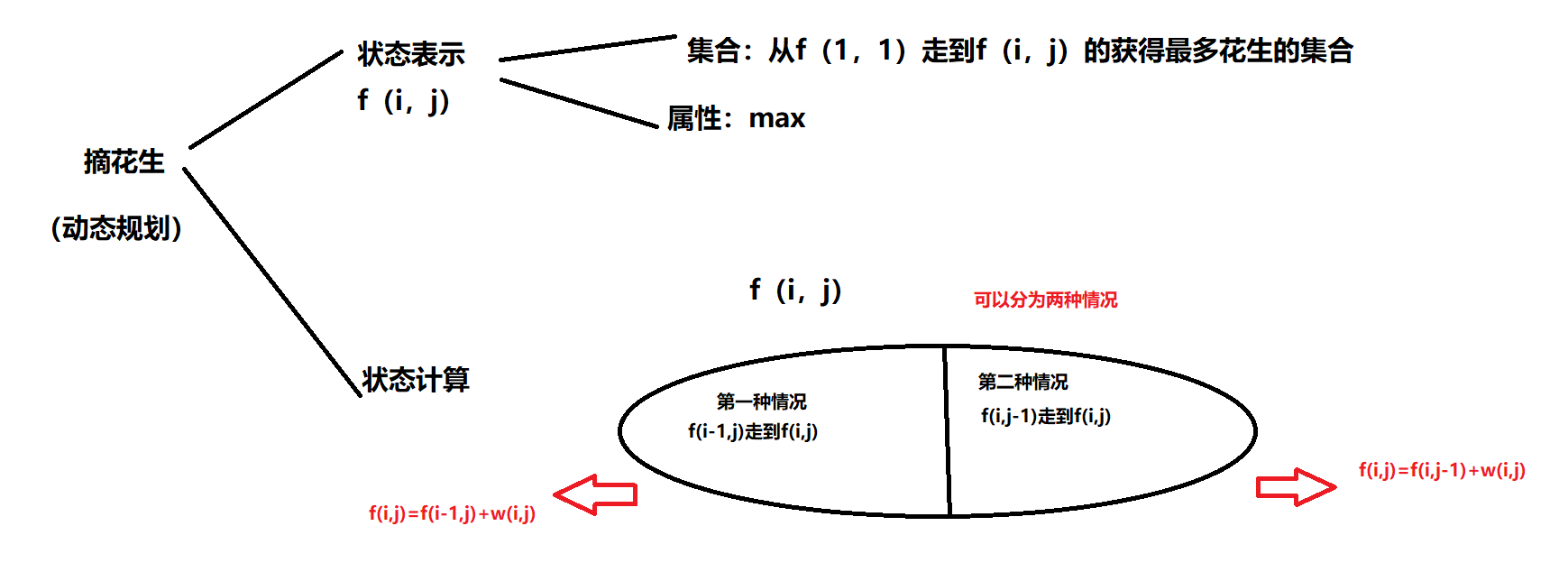
摘花生(简单DP)
Hello Kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。Hel…...
2022济南大学acm新生赛题解
通过答题情况的难度系数: 签到:A 简单:BL 中等:D 困难:CM 极难:KNO A-和 算出n个数的和判断正负性即可!!! 发现很多同学的代码错误:要么sum未赋初值&…...

策略模式教程
策略模式是一种行为型设计模式,它允许在运行时根据不同的情况选择不同的算法实现,从而使得算法可以独立于客户端而变化。本文将介绍策略模式的概念、应用场景、优点和缺点,并提供最佳的代码实践。本文的代码实现将使用Java语言,但…...
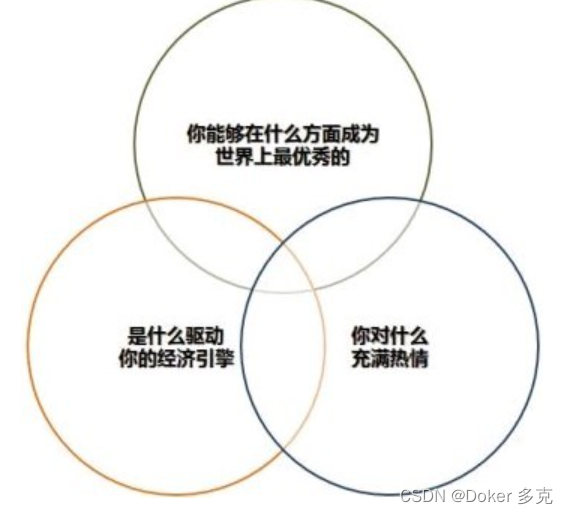
什么是刺猬理念
一、什么是刺猬理念刺猬理念是指把复杂的世界简化成单个有组织性的观点,一条基本原则或一个基本理念,发挥统帅和指导作用。核心是把事情简单化,把所有的挑战和进退维谷的局面压缩为简单的。二、刺猬理念的寓言故事狐狸是一种狡猾的动物&#…...

RPC通信相关
RPCRPC, 远程过程调用(Remote Procedure Call,RPC)是一个计算机通信协议,该协议允许运行于一台计算机的程序程调用另一台计算机的上的程序。通俗讲,RPC通过把网络通讯抽象为远程的过程调用,调用远程的过程就…...
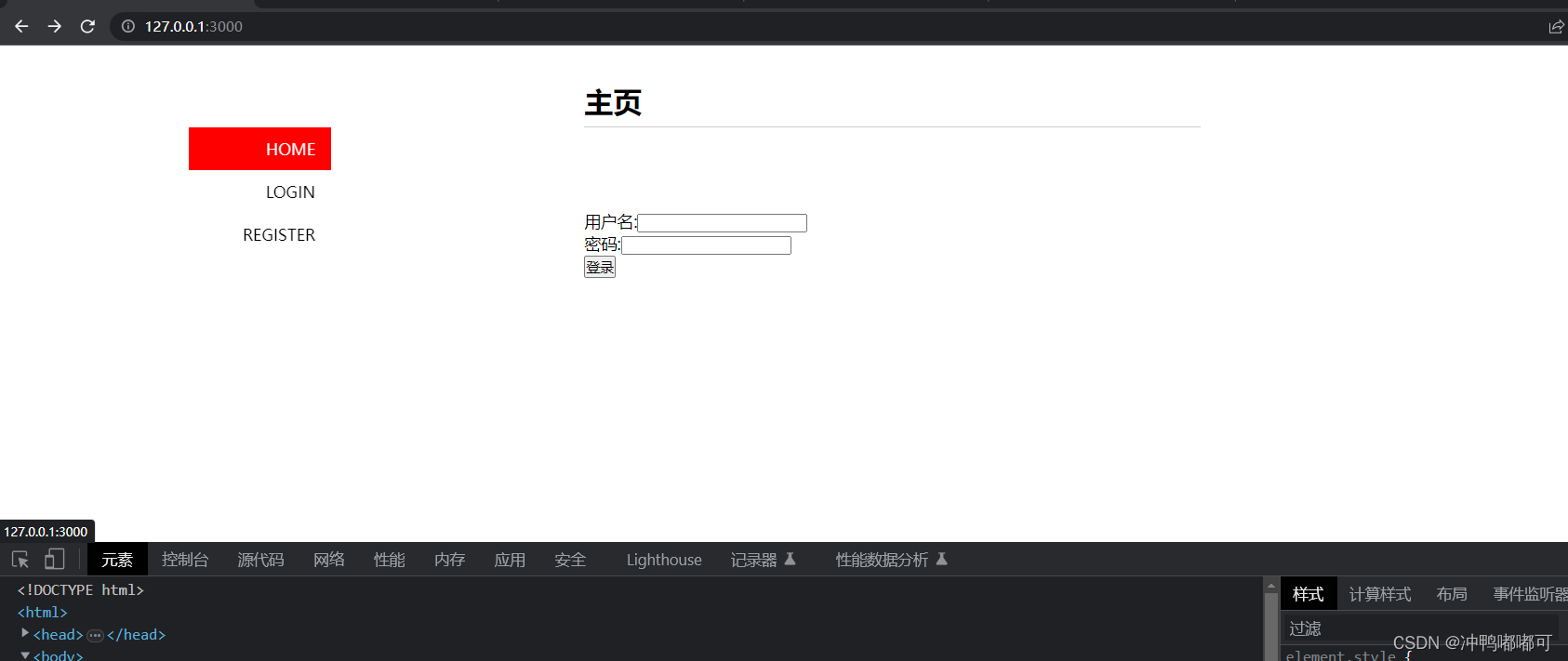
Node.js + MongoDB 搭建博客 -- 登录页面
准备工作 安装Node.js安装express等相关库MongoDB数据库电脑系统:win11 功能分析 搭建一个简单的具有多人注册、登录、发表文章以及登出功能的博客。 设计目标 未登录:主页左侧导航栏显示home、login、register,右侧显示已发表的文章、发…...
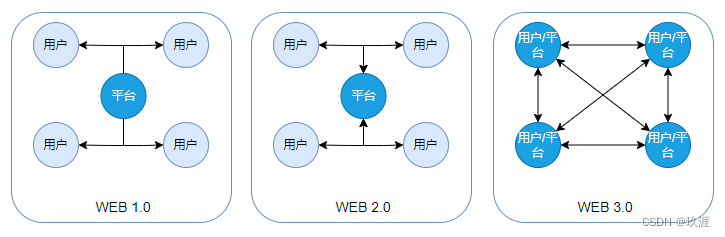
互联网新理念,对于WEB 3.0 你怎么看?
WEB 3.0 这个名词走进大众视野已经有一段时间了,也曾在各个圈子里火热一时,至今各大互联网企业任旧在 WEB 3.0 上不断探索。但关于 WEB 3.0 是什么这个问题,其实大部分人都没有一个比较明确的认知,包括区块链和元宇宙等相关行业的…...

Git使用教程:最详细、最傻瓜、最浅显、真正手把手教
GITGIT版本控制版本控制的意义分布式图形化客户端环境搭建仓库的操作分支使用场景命令远程仓库操作生成公钥命令冲突忽略列表的配置时机配置方式版本回退练习:GIT 版本控制 把文件系统中的文件,按照修改的版本进行记录,进行管理的操作。 版…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
