2024年在分数限制下,选好专业还是选好学校?
分数限制下,选好专业还是选好学校?
24年高考帷幕落下,一场新的思考与选择悄然来临。对于每一位高考考生,学校和专业都是开启大学新生活的两个前置必选项。但有时候“鱼与熊掌不可兼得”,在分数受限的条件下,是选择一个心仪的专业还是选择一个知名度更高的学校?这是一个困扰了众多考生和家长的长期难题。假如是你,你会怎么选?选择专业,意味着你将深入这个领域,直接影响未来的职业发展和个人兴趣的培养;而选择学校,则关系到你将置身于怎样的学术氛围和社交环境中,这对自身的综合素质提升和视野拓展同样至关重要。小编就在本篇文章中给各位学子提一些建议(仅供参考)
一、优先选大学
如果是成绩优越没有弱科的同学,可以考虑报优先选择大学,拥有一个好的学历会让自己以后在出入社会的时候拥有更多的选项,现阶段有些企业招人会对毕业院校有着一定的限制,越是人人向往的单位越是如此。
二、专业解析
首先,我们需要明确的是,专业的选择直接关系到个人的兴趣和未来发展。一个人对某个领域的热爱和兴趣,往往是他在这个领域取得成功的关键。因此,在选择专业时,我们应该充分考虑自己的兴趣所在,和擅长的地方。
在选择专业时需要对专业的就业前景进行深入了解和分析。一些热门专业的就业市场可能饱和,而一些新兴专业可能具有较好的就业前景。考生应该根据自己的兴趣和未来发展趋势来选择专业。
再根据自身条件做出分析,包括个人的兴趣、能力、家庭背景、经济条件等方面。只有综合考虑这些因素,才能做出最为合适的选择。
尽管是专科,还是建议选择公办大学里的专科,一是可以享受本科生的资源,另外也有更大的机会专升本。
以上内容仅个人建议,仅供参考!!!
相关文章:

2024年在分数限制下,选好专业还是选好学校?
分数限制下,选好专业还是选好学校? 24年高考帷幕落下,一场新的思考与选择悄然来临。对于每一位高考考生,学校和专业都是开启大学新生活的两个前置必选项。但有时候“鱼与熊掌不可兼得”,在分数受限的条件下࿰…...
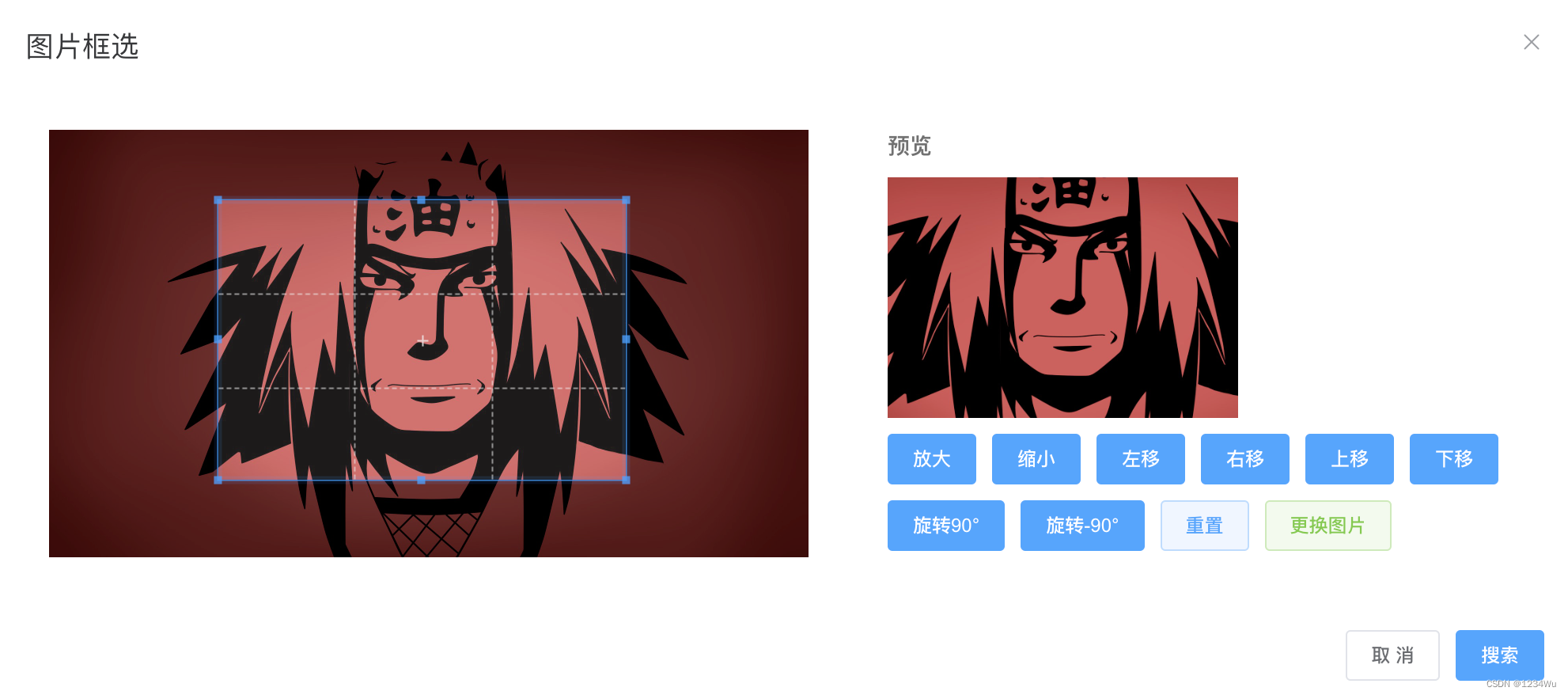
cropperjs 裁剪/框选图片
1.效果 2.使用组件 <!-- 父级 --><Cropper ref"cropperRef" :imgUrl"url" searchImg"searchImg"></Cropper>3.封装组件 <template><el-dialog :title"title" :visible.sync"dialogVisible" wi…...
)
ArkTS开发系列之事件(2.8.2手势事件)
上篇回顾:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件) 本篇内容:ArkTS开发系列之事件(2.8.2手势事件) 一、绑定手势方法 1. 常规手势绑定方法 Text(手势).fontSize(44).gesture(TapGesture().onAct…...
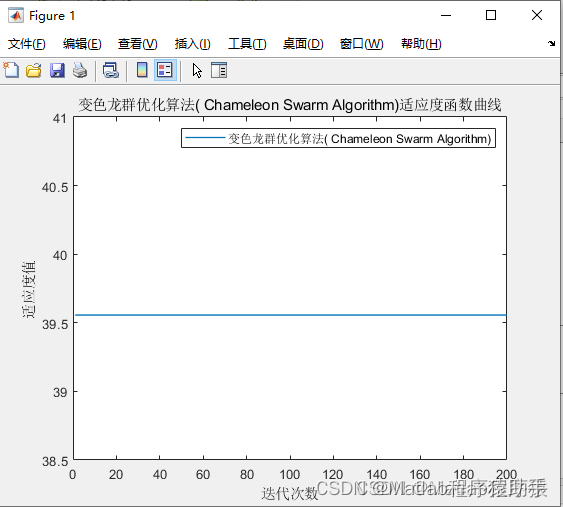
【MATLAB源码-第135期】基于matlab的变色龙群优化算法CSA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 变色龙群优化算法(Chameleon Swarm Algorithm,CSA)是一种新颖的群体智能优化算法,受到自然界中变色龙捕食和社交行为的启发。变色龙以其独特的适应能力而著称,能够根…...

使用Python实现深度学习模型:语言模型与文本生成
语言模型是自然语言处理中的核心任务之一,它们用于预测文本中的下一个单词或生成与输入文本相关的新文本。本文将详细介绍如何使用Python实现一个语言模型,并通过这个模型进行文本生成。 我们将使用TensorFlow和Hugging Face的Transformers库来实现这一任务。 1. 语言模型简…...
)
大数据面试题之Hive(3)
目录 Hive的函数:UDF、UDAF、UDTF的区别? UDF是怎么在Hive里执行的 row_number,rank,dense_rank的区别 Hive count(distinct)有几个reduce,海量数据会有什么问题 HQL:行转列、列转行 一条HQL从代码到执行的过程 了解Hive S…...

华为OD机考题HJ17 坐标移动
前言 应广大同学要求,开始以OD机考题作为练习题,看看算法和数据结构掌握情况。有需要练习的可以关注下。 描述 开发一个坐标计算工具, A表示向左移动,D表示向右移动,W表示向上移动,S表示向下移动。从&am…...

redis修改密码
在Redis中,修改密码通常涉及编辑Redis配置文件或者在运行时通过Redis命令动态修改。 温馨提示:(运行时直接参考第2条) 1.编辑配置文件: 找到Redis配置文件redis.conf,通常位于/etc/redis/或/usr/local/e…...

《昇思 25 天学习打卡营第 7 天 | 模型训练 》
《昇思 25 天学习打卡营第 7 天 | 模型训练 》 活动地址:https://xihe.mindspore.cn/events/mindspore-training-camp 签名:Sam9029 模型训练 本章节-结合前几张的内容所讲-算是一节综合实践 mindscope 框架使用张量 数据类型数据集下载与加载网络构建函…...

HTML/CSS 基础
1、<input type"checkbox" checked> checked 默认选中为复选框 2、表格中的标题<caption> 3、文字标签直接加 title 4、<dl>为自定义列表的整体,包裹<dt><dd> <dt>自定义列表的主题 <dd>主题的每一项内容 5、…...

Linux系统安装Lua语言及Lua外部库
安装Lua Lua语言是一种轻量级、高效且可扩展的脚本语言,具有简洁易学的语法和占用资源少的特点。它支持动态类型,提供了丰富的表达式和运算符,同时具备自动垃圾回收机制和跨平台性。Lua语言易于嵌入到其他应用程序中,并可与其他语…...

前端技术栈学习:Vue2、Vue cli脚手架、ElementUI组件库、Axios
1 基本介绍 (1)Vue 是一个前端框架, 易于构建用户界面 (2)Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或项目整合 (3)支持和其它类库结合使用 (4&#…...
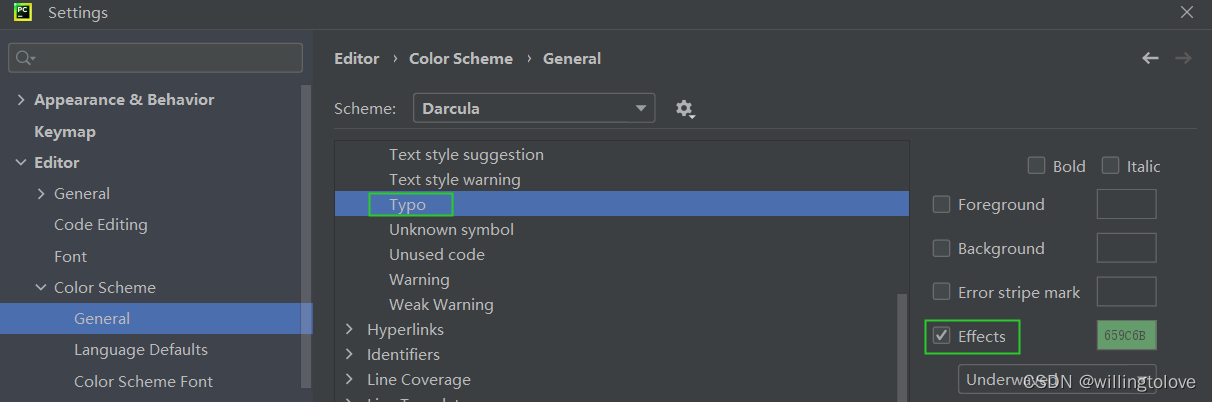
pycharm中取消Typo:In word ‘xxx‘提示(绿色波浪线提示)的方法
#事故现场 使用pycharm写python代码出现绿色波浪线的提示,并提示Typo:In word ‘xxx’,这是pycharm检测到单词拼写错误、不规范; 那如何取消这种提示呢? #解决方法 方法一:Settings → Editor → Inspections → P…...

js中的浅拷贝和深拷贝
浅拷贝Shallow Copy 浅拷贝只复制对象的顶层属性及其引用,而不复制这些引用所指向的对象。如果原始对象中的某个属性是一个对象或数组,那么浅拷贝后的对象将包含对这个内部对象或数组的引用,而不是这个对象或数组的一个新副本。 let obj1 …...

【Linux】常用基本命令
wget网址用于直接从网上下载某个文件到服务器,当然也可以直接从网上先把东西下到本地然后用filezilla这个软件来传输到服务器上。 当遇到不会的命令时候,可以使用man “不会的命令”来查看这个命令的详细信息。比如我想要看看ls这个命令的详细用法&…...
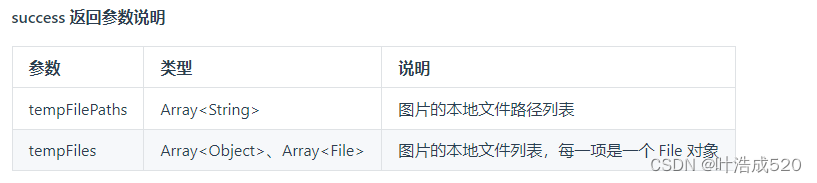
uniapp——上传图片获取到file对象而非临时地址——基础积累
最近在看uniapp的代码,遇到一个需求,就是要实现上传图片的功能 uniapp 官网地址:https://uniapp.dcloud.net.cn/ 上传图片有对应的API: uni.chooseImage方法:https://uniapp.dcloud.net.cn/api/media/image.html#choo…...
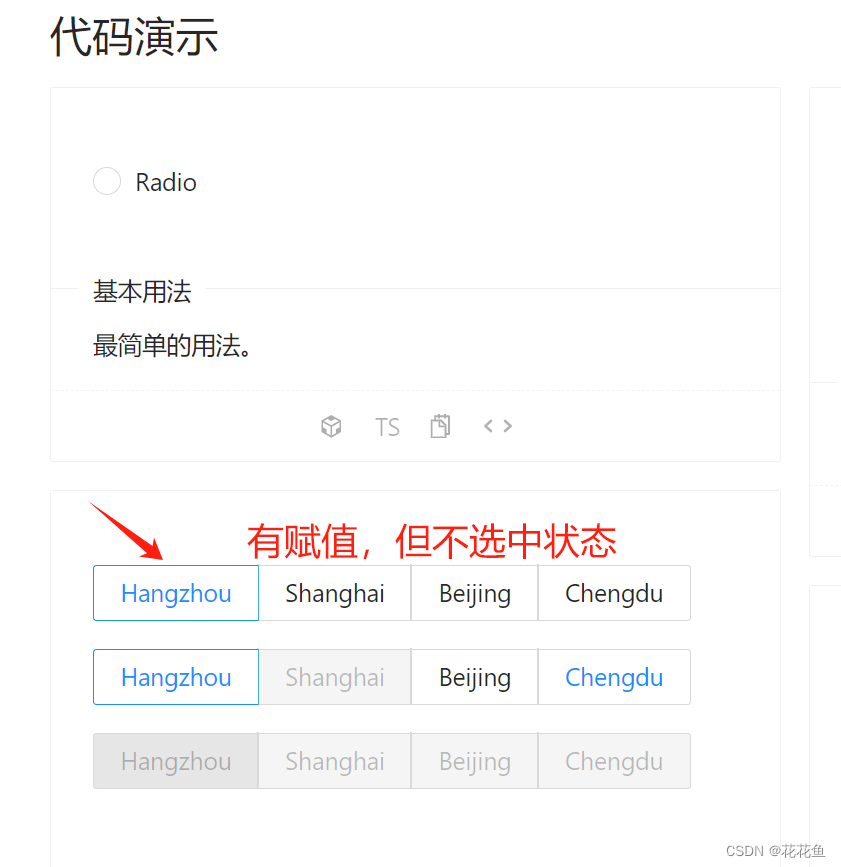
vue3 antdv RadioButton默认值选择问题处理
1、先上官方文档: Ant Design Vue — An enterprise-class UI components based on Ant Design and Vue.js 官方代码: <template><div><div><a-radio-group v-model:value"value1"><a-radio-button value"a…...

最佳实践,一款基于 Flutter 的桌面应用
前言 这篇文章介绍作为一名后端开发人员,快速的入门前端或者客户端一些相关的技术的心得。先来说说为什么作为一名后端开发人员也需要学习一些前端或者客户端相关的技术。通常来说,深耕一个领域没有错,因为社会常常就是这样分工的࿰…...

python第一个多进程爬虫
使用 multiprocessing 模块实现多进程爬取股票网址买卖数据的基本思路是: 定义爬虫函数,用于从一个或多个股票网址上抓取数据。创建多个进程,每个进程执行爬虫函数,可能针对不同的股票或不同的网页。使用 multiprocessing.Queue …...

在Ubuntu 18.04上安装和配置Ansible的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 配置管理系统旨在简化对大量服务器的控制,适用于管理员和运维团队。它们允许您从一个中央位置以自动化的方式控制许多…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
