非递归创建二叉查找树
非递归创建二叉查找树代码。
#include <stdio.h>
#include <stdlib.h>typedef int KeyType;
typedef struct BSTNode{KeyType key;struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;//王道书上的递归写法,代码简单,但是理解有难度
//int BST_Insert1(BiTree &T,KeyType k)
//{
// if(NULL==T)
// { //为新结点申请空间,第一个结点作为树根,后面递归再进入的不是树根,是为叶子结点
// T=(BiTree)malloc(sizeof(BSTNode));
// T->key=k;
// T->lchild=T->rchild=NULL;
// return 1;//代表插入成功
// }
// else if(k==T->key)
// return 0;//发现相同元素,就不插入
// else if(k<T->key)//如果要插入的结点,小于当前结点
// //函数调用结束后,左孩子和原来的父亲会关联起来,巧妙利用了引用机制
// return BST_Insert1(T->lchild,k);
// else
// return BST_Insert1(T->rchild,k);
//}//54,20,66,40,28,79,58
//非递归的创建二叉查找树
int BST_Insert(BiTree &T,KeyType k)
{BiTree TreeNew=(BiTree)calloc(1,sizeof(BSTNode));//新结点申请空间TreeNew->key=k;//把值放入if(NULL==T)//树为空,新结点作为树的根{T=TreeNew;return 1;}BiTree p=T,parent;//p用来查找树while(p){parent=p;//parent用来存p的父亲if(k>p->key){p=p->rchild;}else if(k<p->key){p=p->lchild;}else{return 0;//相等的元素不可以放入查找树,考研不会考相等元素放入问题}}//接下来要判断放到父亲的左边还是右边if(k>parent->key)//放到父亲右边{parent->rchild=TreeNew;}else{//放到父亲左边parent->lchild=TreeNew;}return 1;
}//这里二叉排序树中不放相等元素
void Creat_BST(BiTree &T,KeyType *str,int len)
{int i;for(i=0;i<len;i++){BST_Insert(T,str[i]);//把某一个结点放入二叉查找树}
}void InOrder(BiTree T)
{if(T!=NULL){InOrder(T->lchild);printf("%3d",T->key);InOrder(T->rchild);}
}BiTree BST_Search(BiTree T,KeyType k,BiTree &parent)
{while(T!=NULL&&k!=T->key){parent=T;if(k>T->key){T=T->rchild;}else{T=T->lchild;}}return T;
}//王道书上没有二叉排序树删除代码--考大题的概率没有那么高
//root加引用是因为有可能会删除根结点,从而改变根结点
void DeleteNode(BiTree &root,KeyType x)
{if(NULL==root){return;}if(root->key>x)//当前结点大于要删除的结点,往左子树找{DeleteNode(root->lchild,x);}else if(root->key<x)//当前结点小于要删除的结点,往右子树找{DeleteNode(root->rchild,x);}else{//找到了要删除的结点if(root->lchild==NULL)//左子树为空,右子树直接顶上去{BiTree tempNode=root;root=root->rchild;free(tempNode);}else if(root->rchild==NULL)//右子树为空,左子树直接顶上去{BiTree tempNode=root;root=root->lchild;free(tempNode);}else{//两边都不为空//一般的删除策略是左子树的最大数据或右子树的最小数据代替要删除的结点(这里采用查找左子树最大数据来代替)BiTree tempNode=root->lchild;BiTree parent=root->lchild;while(tempNode->rchild!=NULL){parent=tempNode;//每次tempNode往右走的时候,先保存一下当前位置tempNode=tempNode->rchild;}root->key=tempNode->key;//把tempNode对应的值替换到要删除的值的位置上if(parent!=tempNode){//把tempNode左子树,作为parent的右子树parent->rchild=tempNode->lchild;}else{//当左子树没有右侧结点时//把tempNode左子树,作为root的左子树即可root->lchild=tempNode->lchild;}free(tempNode);}}
}//二叉排序树新建,中序遍历,查找
int main() {BiTree T=NULL;//树根KeyType str[7]={54,20,66,40,28,79,58};//将要进入二叉排序树的元素值Creat_BST(T,str,7);InOrder(T);//中序遍历二叉查找树是由小到大的printf("\n");BiTree search,parent;search=BST_Search(T,40,parent);if(search){printf("find key %d\n",search->key);}else{printf("not find\n");}DeleteNode(T,40);//删除某个结点InOrder(T);printf("\n");return 0;
}相关文章:

非递归创建二叉查找树
非递归创建二叉查找树代码。 #include <stdio.h> #include <stdlib.h>typedef int KeyType; typedef struct BSTNode{KeyType key;struct BSTNode *lchild,*rchild; }BSTNode,*BiTree;//王道书上的递归写法,代码简单,但是理解有难度 //int …...

摄影师危!AI绘画即将降维打击摄影行业
你还以为AI绘画影响的只是插画师行业吗?错了,摄影行业也即将面临技术洗牌 话不多说,先看一下这几张图 你能一眼看出这是AI画的迪丽热巴吗? 你是不是还以为AI绘画只能画点动漫艺术风格?那你就低估了AI的发展速度&…...

ts 中class
class obj{name:stringage:numberconstructor(name:string,age:number){this.name namethis.age age}setname(){this.name 111 } } //新建实例 //构造方法中的this指向调用者,谁new就指向谁 //这个this 指向 o,打印this,可以获取到o身上的…...
Dledger框架日志同步流程)
深度解析RocketMq源码-高可用存储组件(四)Dledger框架日志同步流程
1.绪论 在深度解析RocketMq源码-高可用存储组件(一) raft协议详解-CSDN博客 中讲过,raft协议中,日志同步主要有两个地方,一个是leader会跟follower同步数据,另一个是在新leader诞生的时候,会与…...
ONLYOFFICE 文档开发者版 8.1:API 更新
随着版本 8.1 新功能的发布,我们更新了编辑器、文档生成器和插件的 API,并添加了 Office API 板块。阅读下文了解详情。 ONLYOFFICE 文档是什么 ONLYOFFICE 文档是一个功能强大的文档编辑器,支持处理文本文档、电子表格、演示文稿、可填写…...

Activemq单节点在Windows下的配置部署
1.环境信息 服务器信息jdk版本activemq版本备注Windows Server 2008R2 Enterprisejdk-17_windows-x64_bin.exeapache-activemq-5.18.42.jdk配置 1.下载jdk 地址: Java Downloads | Oracle 中国 2.上传至Windows服务器,点击安装,在选择安装目录页面,选择合适的安装目录即…...
SpringBoot-注解@ImportResource引入自定义spring的配置xml文件和配置类
1、注解ImportResource 我们知道Spring的配置文件是可以有很多个的,我们在web.xml中如下配置就可以引入它们: SprongBoot默认已经给我们配置好了Spring,它的内部相当于已经有一个配置文件,那么我们想要添加新的配置文件怎么办&am…...

GitLab配置免密登录之后仍然需要Git登录的解决办法
GitLab配置免密登录之后仍然需要Git登录的解决办法 因为实习工作需要,要在本地拉取gitlab上的代码,设置了密钥之后连接的时候还需要登录的token,摸索之后有了下面的解决办法。 方法一: 根据报错的提示,去网站上设置个人…...

探索小众爱好:打造个人韧性与特色之路
在这个信息爆炸的时代,我们很容易陷入“千篇一律”的漩涡中,无论是生活方式还是兴趣爱好,似乎都趋向于某种“流行”或“热门”。然而,真正的个性与魅力,往往来源于那些不为大众所知的小众爱好。今天,我想和…...
)
GitHub使用教程(小白版)
看一百篇文章不如自己写一篇 第一步:注册和安装 注册GitHub账号 访问 GitHub官网。点击右上角的 "Sign up" 按钮。按照提示输入你的邮箱、创建用户名和密码,完成注册。 安装Git 访问 Git官网。下载并安装适用于你操作系统的Git。安装…...

深度解析SD-WAN在企业组网中的应用场景
在现代企业快速发展的网络环境中,SD-WAN技术不仅是实现企业各站点间高效连接的关键,也是满足不同站点对互联网、SaaS云应用和公有云等多种业务需求的理想选择。本文将从企业的WAN业务需求出发,对SD-WAN的组网场景进行全面解析,涵盖…...
】Eclipse Nios II SBT 无法从模板创建新应用程序和 BSP)
【INTEL(ALTERA)】Eclipse Nios II SBT 无法从模板创建新应用程序和 BSP
目录 说明 解决方法 说明 您应该能够创建新的应用程序和 BSP 模板包含以下步骤: 选择 Nios II应用程序和 BSP 来自模板。选择您的.sopcinfo 文件并选择模板。从您的工作区单击 选择现有的 BSP 项目。单击 创建。选择所需的 BSP 选项。单击 完成。 但是…...
Vue_cli搭建过程项目创建
概述 vue-cli 官方提供的一个脚手架,用于快速生成一个 vue 的项目模板;预先定义 好的目录结构及基础代码,就好比咱们在创建 Maven 项目时可以选择创建一个 骨架项目,这个骨架项目就是脚手架,我们的开发更加的快速&am…...
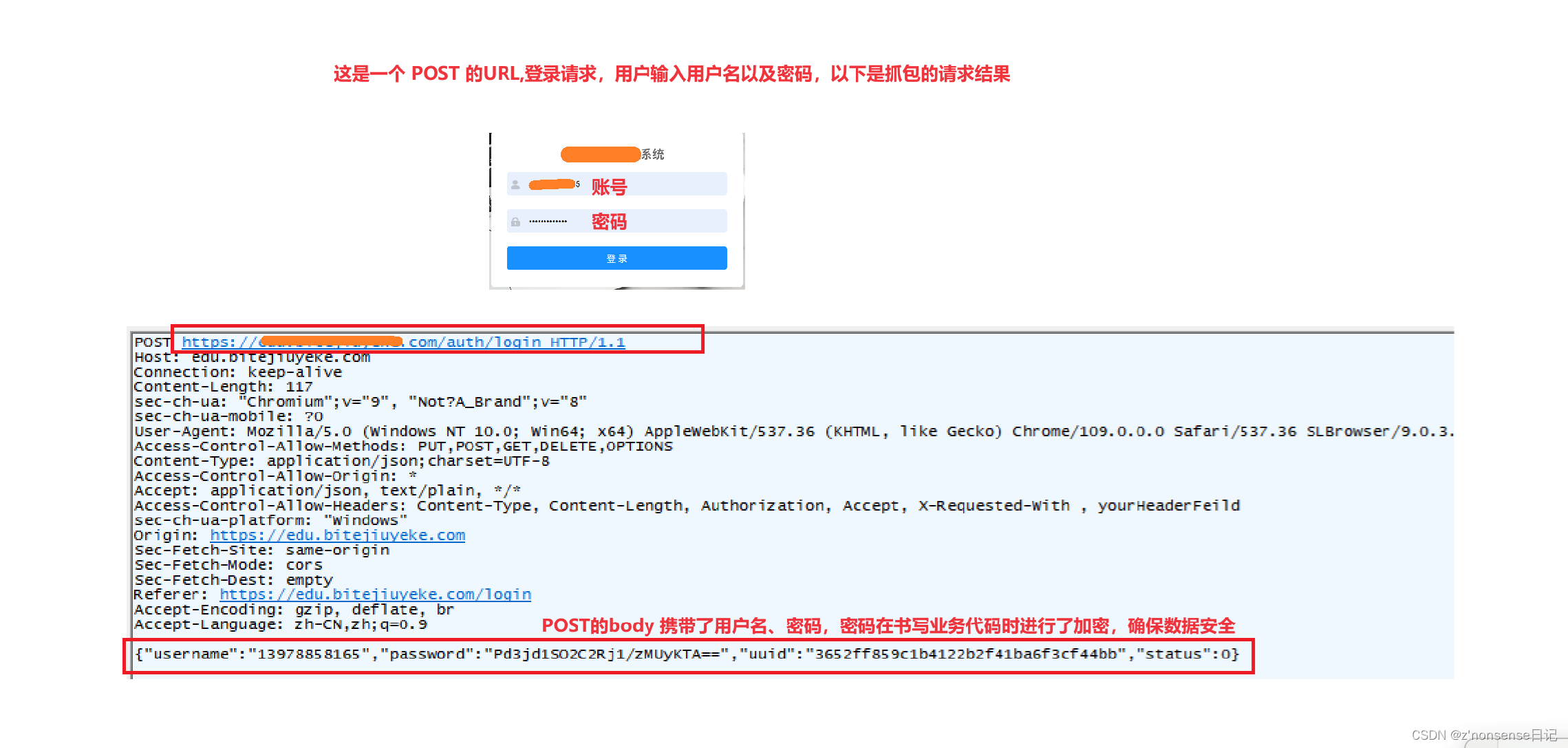
面试题4:POST 比 GET 安全?
不是。HTTP就没有加密功能。 我们知道 GET一般将参数放到URL的查询字符串中,如果是实现登录页面,我们的用户名和密码就直接显示到浏览器的地址栏中了,此时就会轻易的被他人获取账号密码,很不安全。而POST会把参数放到 body 里&am…...
Github生成Personal access tokens及在git中使用
目录 生成Token 使用Token-手工修改 使用Token-自动 生成Token 登录GitHub,在GitHub右上角点击个人资料头像,点击Settings → Developer Settings → Personal access tokens (classic)。 在界面上选择点击【Generate new token】,填写如…...

【BUG记录】条件查询没有查询结果 || MybatisPlus打印查询语句
结论 先说结论,查询没有结果,可能是数据库连接,数据问题之类,最有可能的根本原因是查询语句问题,需要想办法检查查询语句,使用mybatisPlus等自动生成查询语句的框架不能直接看语句,可以依靠日志…...
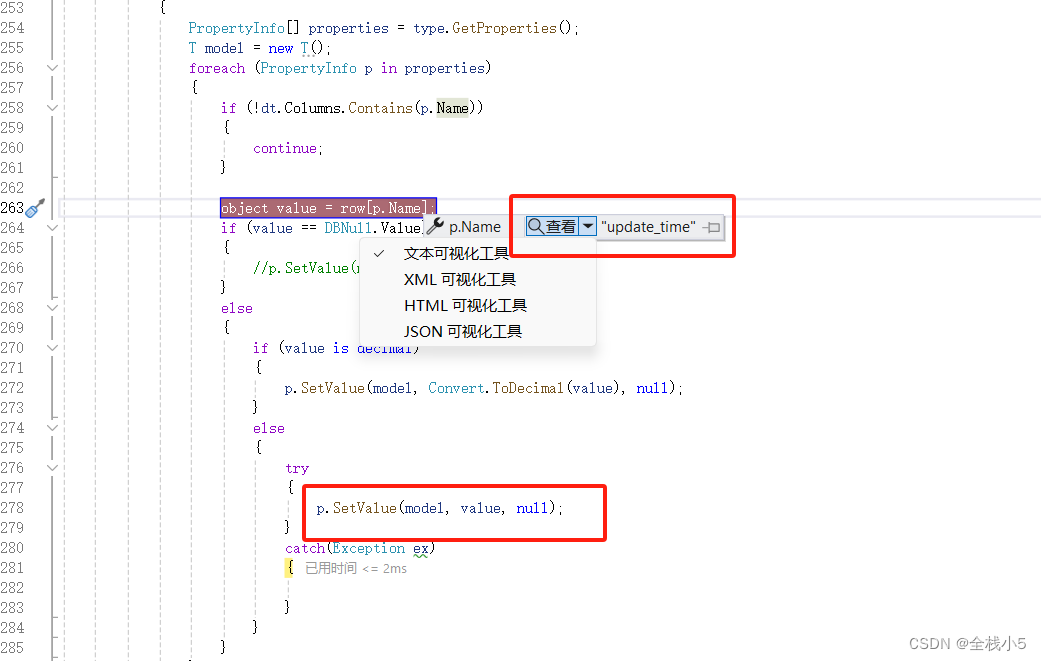
【C#】找不到属性集方法。get只读属性用了反射设置setValue肯定报错
欢迎来到《小5讲堂》 这是《C#》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 背景 找不到属性集方法。get只读属性用了反射设置setValue肯定报错 报错…...
探索ChatGPT在程序员日常工作的多种应用
引言 在现代科技迅猛发展的今天,人工智能的应用已经深入到我们生活和工作的各个方面。作为程序员,我们时常面临大量繁杂的任务,从代码编写、错误调试到项目管理和团队协作,每一项都需要花费大量的时间和精力。近年来,…...

算法与数据结构——时间复杂度详解与示例(C#,C++)
文章目录 1. 算法与数据结构概述2. 时间复杂度基本概念3. 时间复杂度分析方法4. 不同数据结构的时间复杂度示例5. 如何通过算法优化来提高时间复杂度6. C#中的时间复杂度示例7. 总结 算法与数据结构是计算机科学的核心,它们共同决定了程序的性能和效率。在实际开发中…...

面试题3:GET 和 POST 有什么区别?
[!]高频面试题。 GET 和 POST 没有本质区别,可以进行相互代替。 1、GET语义:“从服务器获取数据”;POST语义:“往服务器上提交数据”。[设计初衷,不一定要遵守] 2、发请求时,给服务器传递的数据ÿ…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...
