当前位置： 首页 > news >正文

Linux安全配置

news 2026/2/9 3:12:49

 

  1. 302e416478eb41ff8a5953bc15bcb807.png
  2. 1e5cc82b2de84fdc8898b1c523d4d82b.png
  3. Linux系统审计信息有：系统启动日志（boot.log）、记录用户执行命令日志（acct/pacct）、记录使用su命令的使用（sulog）、记录当前登录的用户信息（utmp）、用户每次登陆和退出信息（wtmp）、最近几次成功登陆及最后一次不成功登陆日志（lastlog）
  4. 最小特权原则指系统中每一个主体只能拥有完成任务所必要的权限集。最小特权管理的目的是系统不应赋予特权拥有者完成任务的额外权限，组织特权乱用。为此，特权的分配原则是“按需使用”这条原则保证系统不会将权限过多的分配给用户，从而可以限制特权造成的危害
  5. Linux系统的who功能是展示登录到当前系统的用户
  6. c084988302c74a8c9fa7c6276ec349ff.png
  7. 口令是系统中认证用户的主要手段，系统安装时默认的口令最小长度是5，但为保证口令不易被猜测攻击，可增加口令的最小长度至少为8.为此需要修改文件/etc/login.defs中的参数PASS MIN LEN 。同时应限制口令的使用时间，保证定期更换口令，建议修改参数PASS MIN DAYS
  8. 特权是用户超越系统访问控制所拥有的权限，特权的管理应按最小化机制，防止特权误用。最小特权原则中每一个主体只能拥有完成任务所必须的权限集。特权的分配原则是“按需使用”，这条原则保证系统不会将权限过多的分配给用户，从而可以限制特权造成的危害
  9. 负载均衡设备就是实现负载均衡的基本设备。具体的均衡的方法可以使用轮询的形式，每个请求按照访问的顺序，逐个循环的分配到三台主机上
  10. /27可以看出掩码是255.255.255.224
  11. Web应用防护系统（WAF）代表了新兴的信息安全技术，用以解决防火墙一类传统设备束手无策的Web应用安全问题。Waf工作在应用层，因此对Web应用防护有明显的优势
  12. 从光纤交换机可以看出应该是SAN网络
  13. 自主访问控制模型、强制访问控制模型、基于角色的访问控制模型常用语操作系统、数据库系统的资源访问
  14. 基于属性的访问控制主要提供分布式网络环境和Web服务的模型访问控制
  15. 基于列的自主访问控制机制是在每个客体上都附加一个可访问它的主体的明细表，它有两种形式，既保护位（这种方法通过对所有主体、主体组以及客体的拥有者指明一个访问模式集合，通常以比特位来表示访问权限）和访问控制表
  16. 676370ece1e74cf0ac97b9e42baa0dc8.png
  17. Windows  IIS  FTP服务器自身提供了三种访问限制技术手段，实现用户账号认证、匿名访问控制以及IP地址限制
  18. 远程登录计算机的协议有telne（23）t和SSH（22），其中telnet以明文方式传输，是一种不安全的协议，SSH提供了保密性服务，所以处于安全考虑，应该选择使用SSH，其中Linux/UNIX服务器的远程安全登录管理的开源工具是OpenSSH
  19. 34d54011d83a4c32be7f9e04bd54e1d7.png
  20. 在Linux系统中，使用ps命令查看受害主机的活动进程；使用who命令查看受害主机的在线用户信息；使用arp命令查看受害主机的ARP地址解析缓存表；使用lsof命令检查系统重进程使用的文件、tcp/udp端口、用户等相关信息
  21. b0f4a20f402a406387a53e044810bff6.png

 

相关文章：

Linux安全配置

Linux系统审计信息有：系统启动日志（boot.log）、记录用户执行命令日志（acct/pacct）、记录使用su命令的使用（sulog）、记录当前登录的用户信息（utmp）、用户每次登陆和退出信…...

编程日记 2024/6/27 6:42:02

vue实现不预览PDF的情况下打印pdf文件

前景：默认情况，实现打印需要根据预览的内容进行打印。 但是当只有打印按钮存在，不预览文件内容的情况下，实现打印的话，可以通过后端接口返回服务器上PDF的地址,前端通过隐藏的iframe标签中src可实现预览功能 主要是根据…...

编程日记 2024/6/27 6:39:59

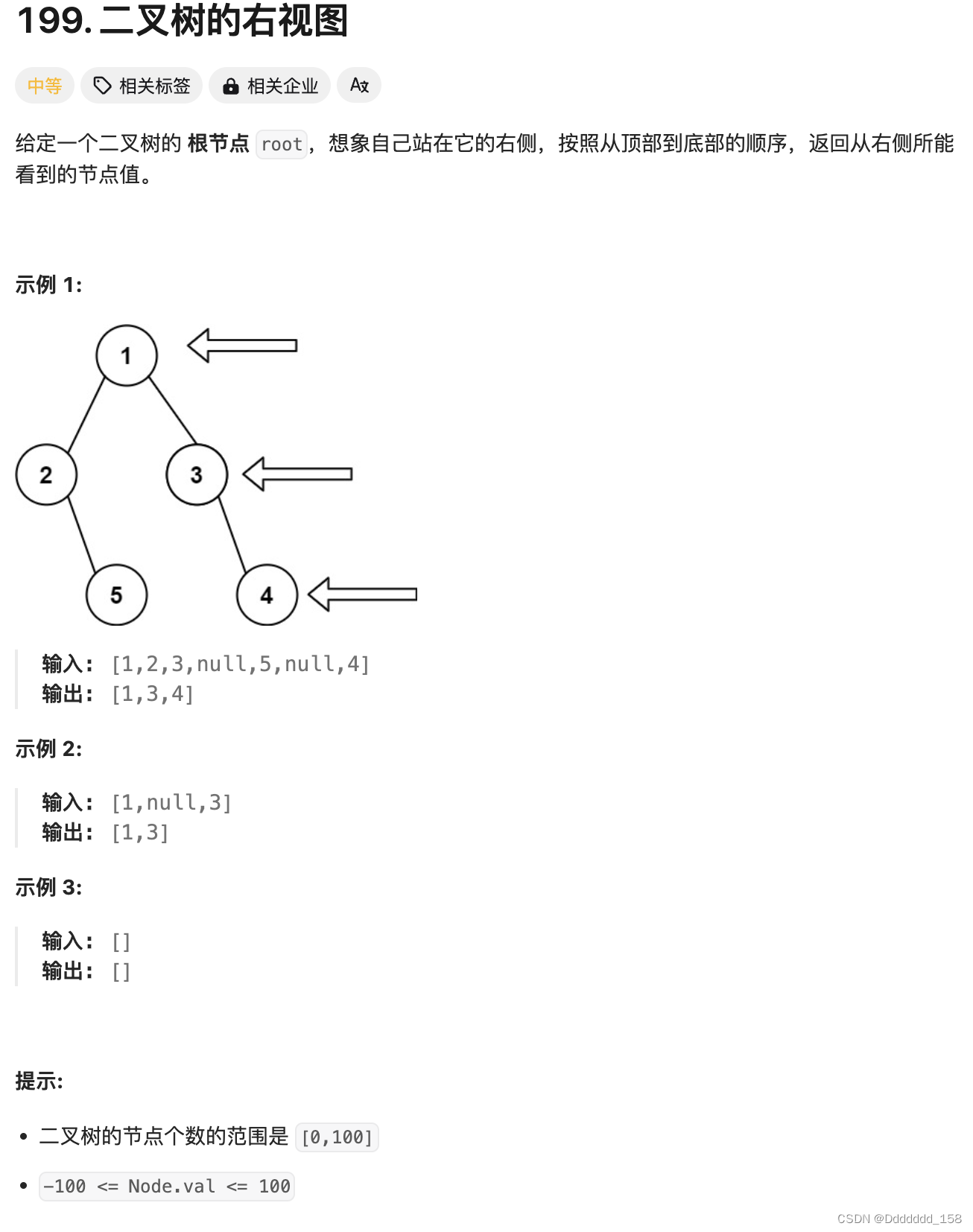
C++ | Leetcode C++题解之第199题二叉树的右视图

题目&#xff1a; 题解&#xff1a; class Solution { public:vector<int> rightSideView(TreeNode* root) {unordered_map<int, int> rightmostValueAtDepth;int max_depth -1;stack<TreeNode*> nodeStack;stack<int> depthStack;nodeStack.push(ro…...

编程日记 2024/6/27 6:38:58

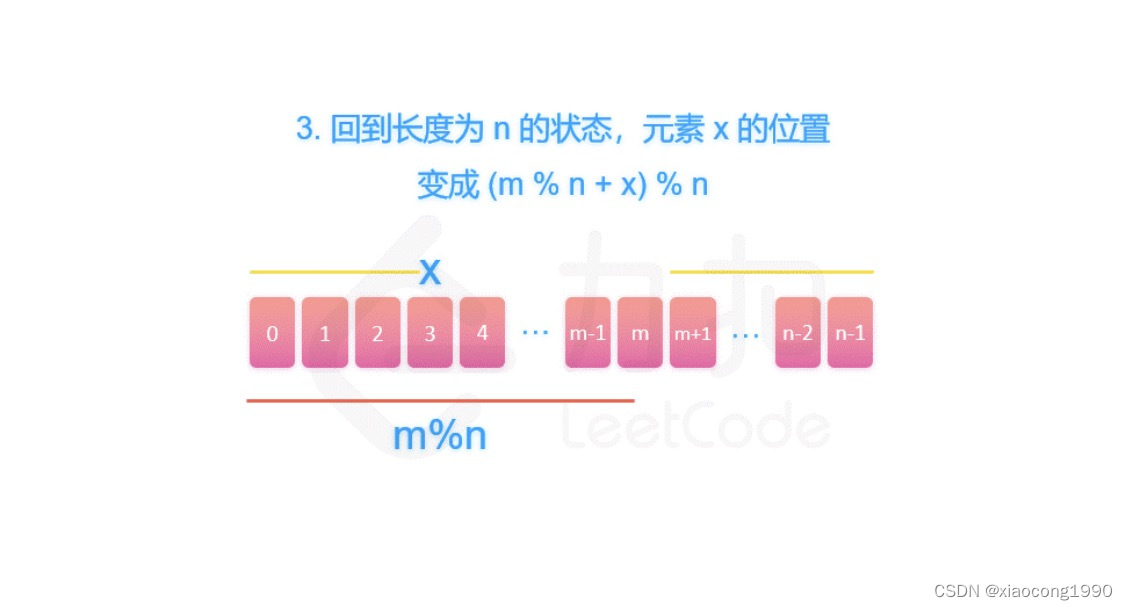
[leetcode]圆圈中最后剩下的数字/ 破冰游戏

. - 力扣&#xff08;LeetCode&#xff09; class Solution {int f(int num, int target) {if (num 1) {return 0;}int x f(num - 1, target);return (target x) % num;} public:int iceBreakingGame(int num, int target) {return f(num, target);} };...

编程日记 2024/6/27 6:36:56

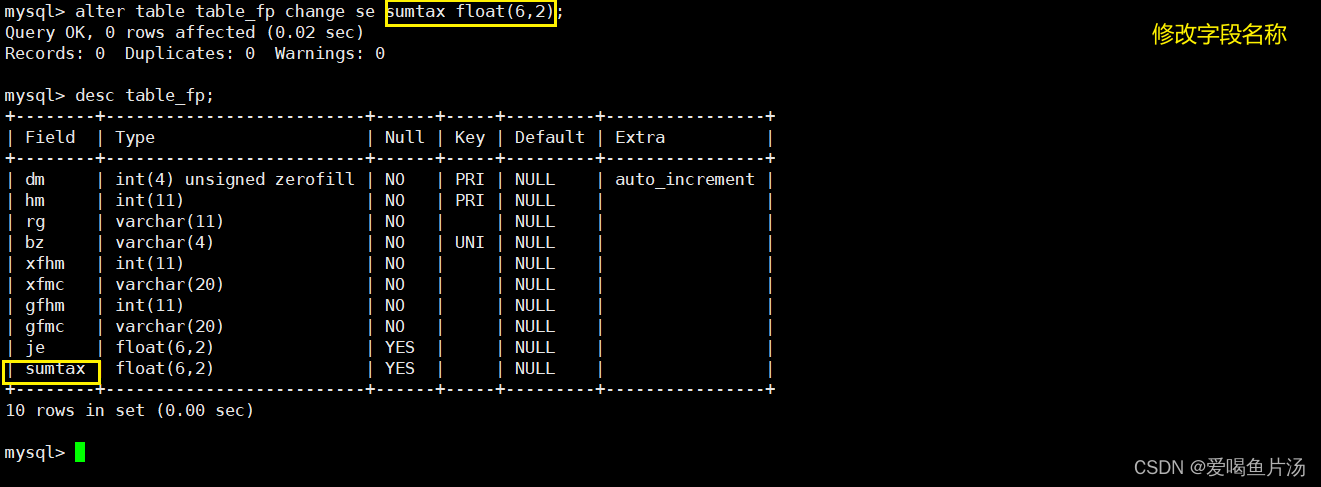
mysql数据库的管理

目录 一、常用的数据类型 二、MySQ数据库基础操作 1、登录数据库 2、查看当前的 MySQL 版本信息及连接用户名 3、查看当前服务器中的数据库 4&#xff0e;查看数据库中包含的表 5&#xff0e;查看表的结构&#xff08;字段&#xff09; 6、MySQL的6大约束属性 三、SQL…...

编程日记 2024/6/27 6:35:54

Java项目分层（持续更新中）

第一次更新时间2024.6.26 分包 实体类 功能类 工具类 分层 实体类层 我们要操作的对象&#xff0c;Book,Student... 控制层 控制请求转发 业务层 处理业务 数据层 连接数据库 处理数据 工具类层 JDBC等工具类 测试层 最终启动项目 明确我们所要做的业务之后&a…...

编程日记 2024/6/27 6:34:53

2024年软件测试面试题大全【答案+文档】

&#x1f345; 视频学习&#xff1a;文末有免费的配套视频可观看 &#x1f345; 点击文末小卡片&#xff0c;免费获取软件测试全套资料&#xff0c;资料在手&#xff0c;涨薪更快 一、面试基础题 简述测试流程&#xff1a; 1、阅读相关技术文档&#xff08;如产品PRD、UI设计…...

编程日记 2024/6/27 6:33:52

数据赋能（131）——体系：数据转换——概述、关注焦点

概述 数据转换是指将数据从一种格式、结构或类型转换为另一种格式、结构或类型的过程。 数据转换操作属于数据整理过程。 它通常涉及数据清洗、数据映射、数据合并、数据拆分等操作&#xff0c;以确保数据的正确性和一致性。 数据转换的目的在于将原始数据转换为更易于处理…...

编程日记 2024/6/27 6:32:51

【自然语言处理系列】掌握jieba分词器：从基础到实战，深入文本分析与词云图展示

本文旨在全面介绍jieba分词器的功能与应用&#xff0c;从分词器的基本情况入手&#xff0c;逐步解析全模式与精确模式的不同应用场景。文章进一步指导读者如何通过添加自定义词典优化分词效果&#xff0c;以及如何利用jieba分词器进行关键词抽取和词性标注&#xff0c;为后续的…...

编程日记 2024/6/27 6:30:49

TikTok短视频矩阵系统

随着数字化时代的到来&#xff0c;短视频已成为人们获取信息、娱乐消遣的重要渠道。TikTok&#xff0c;作为全球最受欢迎的短视频平台之一&#xff0c;其背后的短视频矩阵系统是支撑其成功的关键因素。本文将深入探讨TikTok短视频矩阵系统的构成、功能以及它在新媒体时代中的影…...

编程日记 2024/6/27 6:29:48

码题杯：我会修改图

原题链接&#xff1a;码题集OJ-我会修改图​​​​​​ 题目大意&#xff1a;给你一张n个点&#xff08;编号为1∼n&#xff09;&#xff0c;m条边&#xff08;编号为1∼m&#xff09;的无向图&#xff0c;图上每个点都有一个点权&#xff0c;权值分别为a1​,a2​,…,an​&…...

编程日记 2024/6/27 6:28:46

MongoDB Map-Reduce 简介

MongoDB Map-Reduce 简介 MongoDB 是一个流行的 NoSQL 数据库&#xff0c;它使用文档存储数据&#xff0c;这些数据以 JSON 格式存储。MongoDB 提供了多种数据处理方法&#xff0c;其中 Map-Reduce 是一种用于批量处理和聚合数据的功能强大的工具。Map-Reduce 允许用户对大量数…...

编程日记 2024/6/27 6:27:45

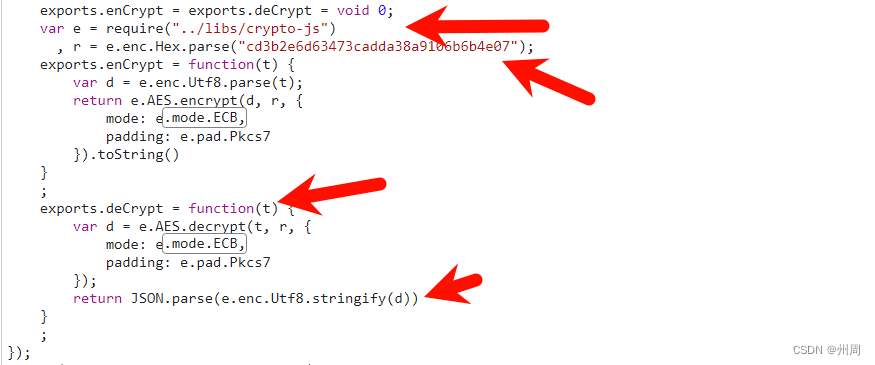
某平台小程序逆向思路整理

一、下载软件 devtools 二、强制打开控制台 根据返回的数据我们得知数据被加密了 找到这个加密的js 发现加密的位置 打断点进入这个加密的方法 之后自定义js。python调用解密即可。...

编程日记 2024/6/27 6:26:44

黑马苍穹外卖6 清理redis缓存+Spring Cache+购物车的增删改查

缓存菜品 后端服务都去查询数据库&#xff0c;对数据库访问压力增大。 解决方式&#xff1a;使用redis来缓存菜品&#xff0c;用内存比磁盘性能更高。 key :dish_分类id String key “dish_” categoryId; RestController("userDishController") RequestMapping…...

编程日记 2024/6/27 6:24:40

鸿蒙开发系统基础能力：【@ohos.systemTime (设置系统时间)】

设置系统时间 本模块用来设置、获取当前系统时间&#xff0c;设置、获取当前系统日期和设置、获取当前系统时区。 说明&#xff1a; 本模块首批接口从API version 7开始支持。后续版本的新增接口&#xff0c;采用上角标单独标记接口的起始版本。 导入模块 import systemTime …...

编程日记 2024/6/27 6:22:39

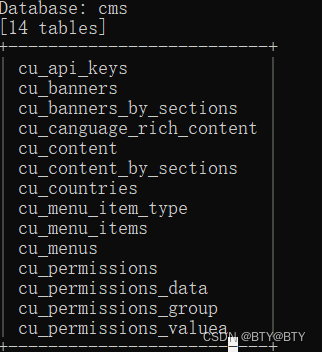
CVE-2020-26048（文件上传+SQL注入）

简介 CuppaCMS是一套内容管理系统&#xff08;CMS&#xff09;。 CuppaCMS 2019-11-12之前版本存在安全漏洞&#xff0c;攻击者可利用该漏洞在图像扩展内上传恶意文件&#xff0c;通过使用文件管理器提供的重命名函数的自定义请求&#xff0c;可以将图像扩展修改为PHP&#xf…...

编程日记 2024/6/27 6:21:36

【面试题】信息系统安全运维要做什么

信息系统安全运维是确保信息系统稳定、可靠、安全运行的一系列活动和措施。 其主要包括以下几个方面&#xff1a; 1.系统监控&#xff1a; 实时监测信息系统的运行状态&#xff0c;如服务器的性能指标、网络流量、应用程序的运行情况等。通过监控工具&#xff0c;及时发现系统…...

编程日记 2024/6/27 6:20:34

引导过程与服务器控制

一、引导过程 1.开机自检 服务器主机开机以后&#xff0c;将根据主板 BIOS 中的设置对 CPU&#xff08;Central Processing Unit&#xff0c; 中央处理器&#xff09;、内存、显卡、键盘等设备进行初步检测&#xff0c;检测成功后根据预设的启动顺序移 交系统控制权&#xff0c…...

编程日记 2024/6/27 6:19:32

前置章节-熟悉Python、Numpy、SciPy和matplotlib

目录 一、编程环境-使用jupyter notebook 1.下载homebrew包管理工具 2.安装Python环境 3.安装jupyter 4.下载Anaconda使用conda 5.使用conda设置虚拟环境 二、学习Python基础 1.快排的Python实现 (1)列表推导-一种创建列表的简洁方式 (2)列表相加 2.基本数据类型及运…...

编程日记 2024/6/27 6:18:32

在Ubuntu上安装和配置配置服务器防火墙（CSF）的方法

前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 简介 Config Server Firewall&#xff08;CSF&#xff09;是大多数 Linux 发行版和基于 Linux 的 VPS 的免费高级防火墙。除了基本的防…...

编程日记 2024/6/27 6:17:30

浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）

✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义&#xff08;Task Definition&…...

编程新知 2026/2/8 15:03:14

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

全球首个30米分辨率湿地数据集(2000—2022)

数据简介 今天我们分享的数据是全球30米分辨率湿地数据集&#xff0c;包含8种湿地亚类&#xff0c;该数据以0.5X0.5的瓦片存储&#xff0c;我们整理了所有属于中国的瓦片名称与其对应省份&#xff0c;方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

编程新知 2026/1/31 17:15:25

BCS 2025｜百度副总裁陈洋：智能体在安全领域的应用实践

6月5日&#xff0c;2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席&#xff0c;并作《智能体在安全领域的应用实践》主题演讲&#xff0c;分享了在智能体在安全领域的突破性实践。他指出&#xff0c;百度通过将安全能力…...

编程新知 2026/2/1 11:33:19

深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南

&#x1f680; C extern 关键字深度解析&#xff1a;跨文件编程的终极指南 &#x1f4c5; 更新时间&#xff1a;2025年6月5日 &#x1f3f7;️ 标签&#xff1a;C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言&#x1f525;一、extern 是什么&#xff1f;&…...

编程新知 2026/2/1 6:50:07

华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建

华为云FlexusDeepSeek征文&#xff5c;DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色&#xff0c;华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型&#xff0c;能助力我们轻松驾驭 DeepSeek-V3/R1&#xff0c;本文中将分享如何…...

编程新知 2026/2/2 2:30:58

ios苹果系统，js 滑动屏幕、锚定无效

现象&#xff1a;window.addEventListener监听touch无效&#xff0c;划不动屏幕&#xff0c;但是代码逻辑都有执行到。 scrollIntoView也无效。 原因&#xff1a;这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作&#xff0c;从而会影响…...

编程新知 2026/2/4 19:47:03

保姆级教程：在无网络无显卡的Windows电脑的vscode本地部署deepseek

文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama&#xff08;有网络的电脑&#xff09;2.2.3 安装Ollama&#xff08;无网络的电脑&#xff09;2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

编程新知 2026/2/6 16:59:24

【Redis】笔记｜第8节｜大厂高并发缓存架构实战与优化

缓存架构 代码结构 代码详情 功能点&#xff1a; 多级缓存&#xff0c;先查本地缓存&#xff0c;再查Redis&#xff0c;最后才查数据库热点数据重建逻辑使用分布式锁&#xff0c;二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

编程新知 2026/1/26 3:45:28