二叉树公共最近祖先
文章目录
- 1. **二叉搜索树(Binary Search Tree, BST)**
- 2. **一般二叉树**
- **递归方法**:
- **迭代方法**:
- 案例展示
- 二叉搜索树(BST)中查找LCA
- 一般二叉树中查找LCA
- 1. **使用哈希表存储父节点信息**
- 2. **处理多个查询**
- 3. **异常处理**
- 结论
在计算机科学中,特别是在数据结构和算法领域,“最近公共祖先”(Lowest Common Ancestor,LCA)是一个在有根树或有向无环图中的概念。对于有根树 ( T ) 的两个结点 ( p ) 和 ( q ),最近公共祖先指的是树中的一个结点 ( x ),满足 ( x ) 是 ( p ) 和 ( q ) 的共同祖先,并且 ( x ) 的深度尽可能大。
在二叉树中寻找最近公共祖先的算法可以分为两种情况:
1. 二叉搜索树(Binary Search Tree, BST)
在二叉搜索树中,可以利用其特性简化查找过程:
- 如果 ( p ) 和 ( q ) 分别位于当前节点的左右两侧,则当前节点即为 LCA。
- 如果 ( p ) 和 ( q ) 都在当前节点的左侧,则在其左子树中继续查找。
- 如果 ( p ) 和 ( q ) 都在当前节点的右侧,则在其右子树中继续查找。
2. 一般二叉树
在一般的二叉树中,没有像 BST 那样的顺序关系,因此需要使用递归或者迭代的方法来遍历树并查找 LCA。
递归方法:
- 从根节点开始递归地搜索 ( p ) 和 ( q )。
- 如果当前节点等于 ( p ) 或 ( q ),则返回当前节点。
- 如果在左子树中找到了 ( p ) 或 ( q ),则返回左子树的结果。
- 如果在右子树中找到了 ( p ) 或 ( q ),则返回右子树的结果。
- 如果左子树和右子树都返回了非空结果,则说明 ( p ) 和 ( q ) 分别位于当前节点的左右两侧,所以当前节点就是 LCA。
- 如果左子树或右子树返回了空结果,而另一个子树返回了非空结果,则返回非空结果。
迭代方法:
- 使用栈来模拟递归过程,同时需要额外的空间来记录每个节点的父节点。
- 通过回溯到根节点的方式,找出 ( p ) 和 ( q ) 的路径,然后比较这两条路径找到最后一个相同的节点,这个节点就是 LCA。
在实现这类算法时,需要考虑各种边界条件,比如当 ( p ) 或 ( q ) 之一不存在于树中时如何处理等。通常情况下,算法设计时会假设 ( p ) 和 ( q ) 都存在于树中。如果需要处理这种情况,可以在遍历过程中检查是否已经找到了两个节点。
案例展示
接下来我将提供一些具体的代码实现示例,以便你更好地理解如何在二叉树中查找最近公共祖先(LCA)。我们将分别展示二叉搜索树(BST)和一般二叉树中查找LCA的Python代码实现。
二叉搜索树(BST)中查找LCA
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef lowestCommonAncestor(root, p, q):while root:if root.val > p.val and root.val > q.val: # 如果 p 和 q 都小于当前节点,向左子树移动root = root.leftelif root.val < p.val and root.val < q.val: # 如果 p 和 q 都大于当前节点,向右子树移动root = root.rightelse: # 当前节点就是 LCAreturn root
一般二叉树中查找LCA
class Solution:def lowestCommonAncestor(self, root, p, q):self.p_found = Falseself.q_found = Falseresult = self._helper(root, p, q)# 确保 p 和 q 都存在二叉树中if not self.p_found or not self.q_found:return Nonereturn resultdef _helper(self, node, p, q):if not node:return None# 检查当前节点是不是 p 或 qif node == p:self.p_found = Truereturn nodeif node == q:self.q_found = Truereturn nodeleft = self._helper(node.left, p, q)right = self._helper(node.right, p, q)# 如果 p 和 q 分别在左右子树中,那么当前节点就是 LCAif left and right:return node# 否则返回找到的节点(left 或 right)return left or right
在上述代码中,TreeNode 类用于定义二叉树的节点,而 lowestCommonAncestor 函数实现了LCA的查找逻辑。在一般二叉树的实现中,我们使用了一个辅助函数 _helper 来递归地查找 p 和 q,并使用布尔变量 p_found 和 q_found 来追踪是否已经找到了这两个节点。
希望这些代码示例能帮助你理解如何在二叉树中实现LCA的查找。如果有任何疑问或需要进一步的解释,请随时提问!
在上一部分中,我们讨论了二叉树中查找最近公共祖先(LCA)的基本算法和代码实现。现在,让我们深入探讨一些高级主题和优化技巧,以提高算法效率和代码可读性。
1. 使用哈希表存储父节点信息
在一般二叉树中,如果我们能够预先构建一个哈希表来存储每个节点的父节点信息,那么查找LCA的过程可以更加直观和高效。这种方法特别适用于需要频繁查询LCA的场景。
def build_parent_map(root, parent_map):stack = [(root, None)]while stack:node, parent = stack.pop()parent_map[node] = parentif node.left:stack.append((node.left, node))if node.right:stack.append((node.right, node))def find_path(parent_map, target, path):while target:path.append(target)target = parent_map[target]def lowestCommonAncestor(root, p, q):parent_map = {}build_parent_map(root, parent_map)path_p = []path_q = []find_path(parent_map, p, path_p)find_path(parent_map, q, path_q)i = 0while i < len(path_p) and i < len(path_q) and path_p[i] == path_q[i]:i += 1return path_p[i-1]
这段代码首先构建了一个哈希表 parent_map 来存储每个节点的父节点,然后分别找到 p 和 q 到根节点的路径,并找到这两条路径上的最后一个相同节点,即为 LCA。
2. 处理多个查询
当需要处理多个LCA查询时,预处理树的信息(如父节点、深度等)可以显著提升性能。例如,使用动态规划技术可以计算出每个节点的深度以及每个节点的(2^i)倍的祖先节点,这样在查询时可以快速跳过多个层级。
3. 异常处理
在实际应用中,应考虑各种可能的异常情况,例如:
- 如果
p或q中的一个或两个不在树中,应如何处理? - 如何处理
p和q相同的情况?
在代码实现中,可以通过添加适当的边界检查来处理这些情况,确保算法的健壮性和正确性。
结论
查找二叉树中的最近公共祖先是一个经典问题,不仅在算法竞赛中常见,也是许多实际应用的基础。通过理解不同类型的二叉树和优化策略,你可以更有效地解决这一问题,并将其应用于更广泛的场景中。希望上述内容对你有所帮助!如果有任何疑问或需要进一步讨论的地方,欢迎随时提问。
————————————————
最后我们放松一下眼睛

相关文章:

二叉树公共最近祖先
文章目录 1. **二叉搜索树(Binary Search Tree, BST)**2. **一般二叉树****递归方法**:**迭代方法**: 案例展示二叉搜索树(BST)中查找LCA一般二叉树中查找LCA1. **使用哈希表存储父节点信息**2. **处理多个查询**3. **异常处理**结…...

智慧运维系统指导规范
随着信息技术的迅猛发展,智慧运维系统在现代企业中扮演着越来越重要的角色。为了提高运维效率、保障系统稳定运行,并制定一套科学、合理的智慧运维系统指导规范至关重要。本规范旨在为企业提供一套全面、系统的智慧运维管理方法和操作准则,以…...

最新自助下单彩虹云商城系统源码,含小储云商城模板免授权
最新彩虹商城源码,含小储云商城模板免授权,试用了一下还行,具体的大家可以看看 源码下载:https://download.csdn.net/download/m0_66047725/89405387 更多资源下载:关注我。...

头条系统-05-延迟队列精准发布文章-概述添加任务(db和redis实现延迟任务)、取消拉取任务定时刷新(redis管道、分布式锁setNx)
文章目录 延迟任务精准发布文章1)文章定时发布2)延迟任务概述2.1)什么是延迟任务2.2)技术对比2.2.1)DelayQueue2.2.2)RabbitMQ实现延迟任务2.2.3)redis实现 3)redis实现延迟任务4)延迟任务服务实现4.1)搭建heima-leadnews-schedule模块4.2)数据库准备4.3)安装redis4.4)项目集成…...

.gitignore git添加忽略文件
在项目的根目录下创建一个名为 .gitignore 的文件。在这个文件中,列出您希望Git忽略的文件和文件夹的名称或模式。 下面是一些基本的步骤和规则: 创建 .gitignore 文件:在项目根目录下创建一个名为 .gitignore 的文件。如果没有这个文件&…...

面向遥感图像的多阶段特征融合目标检测方法
源自:电子学报 作者:陈立 张帆 郭威 黄赟 注:若出现无法显示完全的情况,可 V 搜索“人工智能技术与咨询”查看完整文章 摘 要 遥感图像目标具有多尺度、大横纵比、多角度等特性,给传统的目标检测方法带来了新的…...
操作系统面试篇一
很多读者抱怨计算操作系统的知识点比较繁杂,自己也没有多少耐心去看,但是面试的时候又经常会遇到。所以,我带着我整理好的操作系统的常见问题来啦!这篇文章总结了一些我觉得比较重要的操作系统相关的问题比如 用户态和内核态、系统…...
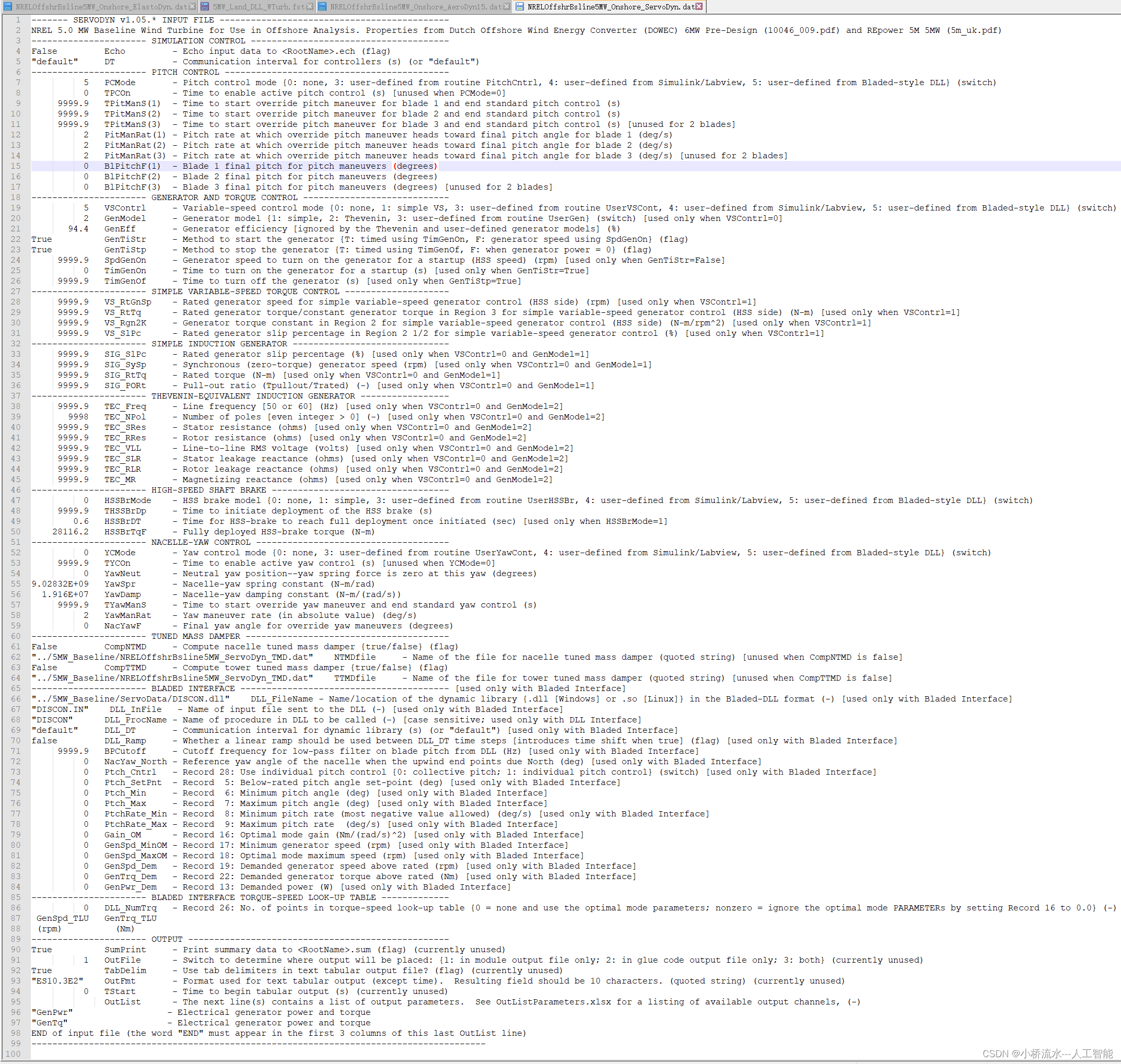
OPenFast软件中的NRELOffshrBsline5MW_Onshore_ServoDyn.dat文件详解
我先简单概括一下,后续我再详细总结:文件“NRELOffshrBsline5MW_Onshore_ServoDyn.dat”是用于NREL 5.0 MW基准风力发电机的ServoDyn模块的输入文件。它定义了仿真控制、变桨控制、发电机和扭矩控制、偏航控制以及输出设置等各种参数。以下是主要内容的总…...

搭建rtmp/rtsp流媒体服务器的步骤
很多文章介绍使用ffmpeg推送和拉流,执行推流命令: D:\software\ffmpeg-7.0.1-full_build\bin\ffmpeg.exe -re -stream_loop -1 -i "D:\Video\汪汪队立大功\S07\001.mp4" -vcodec h264 -acodec aac -f flv rtmp://127.0.0.1/live/test110 经常…...

vue自定义事件传递数据
页面应用一个组件,采用自定义事件来传递参数 $emit是Vue实例的一个方法,它用于触发自定义事件。这些事件可以被父组件监听到,从而实现子组件向父组件的通信。 这种方法的好处在于,它可以让数据的流动保持单向,有助于…...
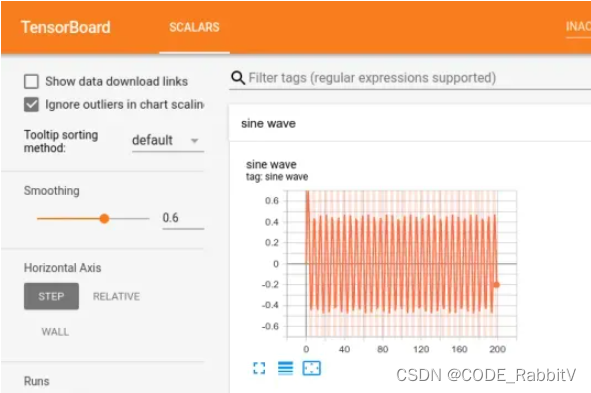
TensorBoard 安装与启动
安装:pip install tensorboard启动:tensorboard --logdir<events_directory_name> events_directory_name 为运行 tensorboard 后,产生的 events 文件所在的路径 博客参考:TensorBoard最全使用教程...

云计算运维工程师的突发状况处理
云计算运维工程师在应对突发的故障和紧急情况时,需要采取一系列迅速而有效的措施来最小化服务中断的时间并恢复系统的稳定性。 以下是一些关键步骤和策略: 快速响应: 立即识别并确认故障的性质和范围。通知团队成员和相关的利益相关者,确保所有人了解当前情况。故障诊断:…...

【CSS in Depth 2 精译】1.6 本章小结
1.6 本章小结 浏览器遵循层叠规则来确定哪些样式在哪些元素上生效;选择器优先级由选择器中的 id 数、class 类的个数以及标签名的个数来共同确定。优先级更高的声明将覆盖较低声明;当某些属性没有层叠值时,它们会从父元素继承一个样式值。这…...

FFmpeg源码:ff_h2645_extract_rbsp函数分析
一、ff_h2645_extract_rbsp函数的声明 ff_h2645_extract_rbsp函数的声明放在FFmpeg源码(本文演示用的FFmpeg源码版本为5.0.3,该ffmpeg在CentOS 7.5上通过10.2.1版本的gcc编译)的头文件libavcodec/h2645_parse.h中。 /*** Extract the raw (u…...
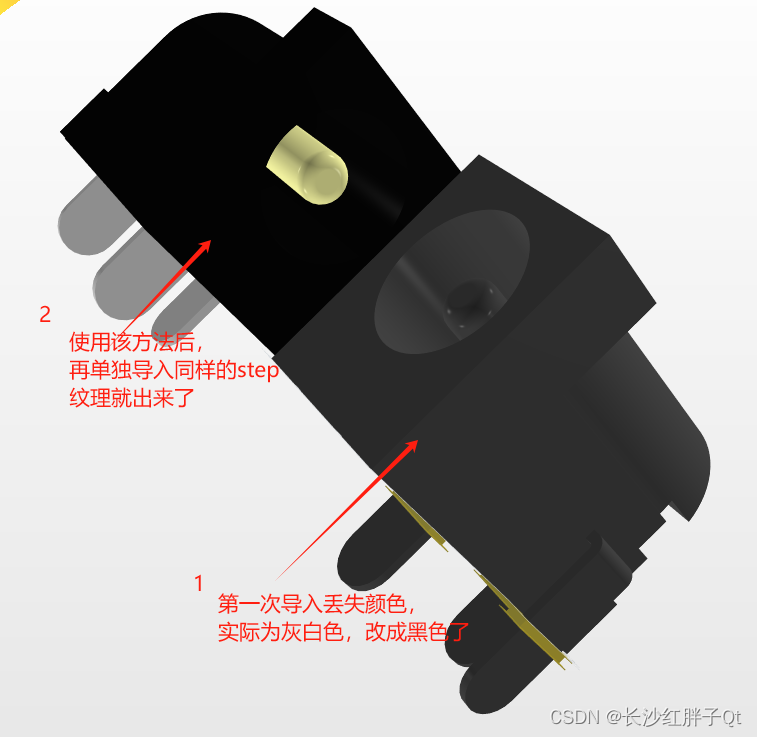
关于 AD21导入电子元器件放置“3D体”STEP模型失去3D纹理贴图 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/139969415 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

【JAVA】利用Redisson和Spring实现高效物联温度控制链路,确保温度调节的准确性和效率,定时链路执行使用案例,一环扣一环
主要功能和场景 柔性调温策略:这个类主要用于管理一个温度调节流程,通过不同的策略(如策略1和策略2)来调节温度,确保设备或环境中的温度达到预设的目标。 紧急停止机制:在流程执行过程中,如果需…...

yolov8部署资料
1.labelImg安装: labelImg的安装过程可以参照以下步骤进行,这里以Windows操作系统为例: 1. 检查Python环境 首先,需要确认你的电脑上是否已经安装了Python。你可以通过Win R打开windows“运行”对话框,输入cmd&#x…...

迅为RK3588开发板支持LVDS信号,标准 HDMI信号,IMIPI信号
性能强--iTOP-3588开发板采用瑞芯微RK3588处理器,是全新一代ALoT高端应用芯片,采用8nm LP制程,搭载八核64位CPU,四核Cortex-A76和四核Cortex-A55架构,主频高达2.4GHZ,8GB内存,32GB EMMC。 四核心…...
页面开发感想
页面开发 1、 前端预览 2、一些思路 2.1、首页自定义element-plus的走马灯 :deep(.el-carousel__arrow){border-radius: 0%;height: 10vh; }需要使用:deep(标签)才能修改样式 或者 ::v-deep 标签 2.2、整体设计思路 <template><div class"card" style&…...

TikTok达人合作ROI分析:品牌如何评估带货效果
在当今的数字营销时代,TikTok已经成为品牌推广和消费者互动的重要平台。通过与TikTok达人的合作,品牌可以有效地提升其市场影响力和销售额。其中,评估这些合作的投入产出比(ROI)对于品牌来说是至关重要的。本文Nox聚星…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
