最大团问题--回溯法
一、相关定义
给定一个无向图 ,其中 V 是图的顶点集,E图的边集
完全图:如果无向图中的任何一对顶点之间都有边,这种无向图称为完全图
完全子图:给定无向图 ,如果
,且对应任意
且
,则称U是G的完全子图。(即完全子图中的任意两个顶点之间都有边)
团(最大完全子图):U 是 G 的团当且仅当 U 不包含在G的更大完全子图中。若存在一个最大完全子图包含U,那么 U 不是一个团。
最大团:G 中所包含顶点数最多的团
最大团问题是一个NP-C问题,无法在多项式时间内求出最大团,通常只能在数据规模较小的情况下适用。
二、回溯法
算法思路:通过回溯的方法考虑每个顶点是否加入最大团的情况,因此算法的时间复杂度为 。
首先设最大团为一个空团,往其中加入一个节点,然后依次考虑每个节点,查看该节点是否能够加入团(判断方法:该节点应当与团内每一个节点有一条边),随后向下一节点搜索,直至递归所有节点并回溯结束。
剪枝策略:如果剩下未考虑的节点n加上当前团内的节点数小于此时计算的最大团节点数,则不需要再进行搜索。
对于一个无向图 G={V,E}
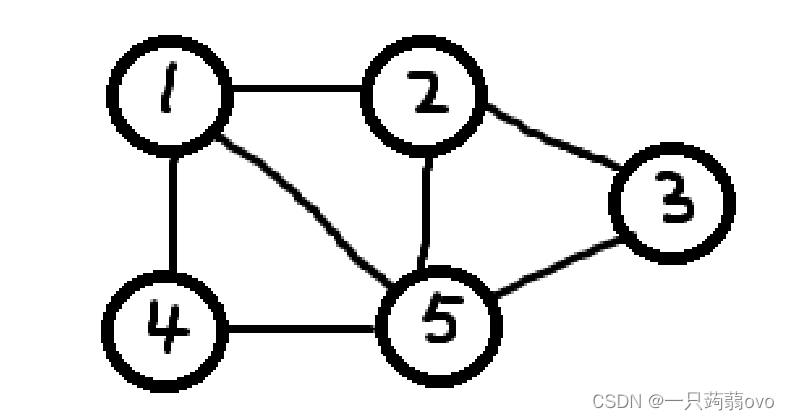
可以看出最大团为 { 1 , 2 , 5 } { 1 , 4 , 5 } { 2 , 3 , 5 } 即最大团不唯一。对于一个完全子图{1,2},不是一个团,因为存在包含 {1,2} 的更大的完全子图 {1,2,5} (区分完全子图和团)
下图:左子树时表示考虑节点i加入团中 , 右子树则不在团中
cn为当前团中在节点个数,bestn当前最大团中在节点个数
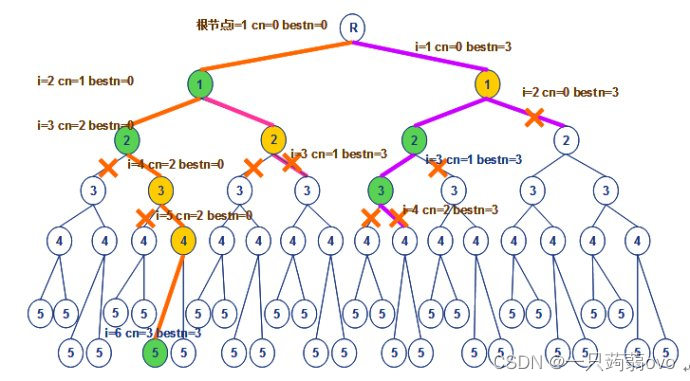
① 考虑 节点1 时加入当前团时,符合团的条件,则继续深搜考虑节点2,(1,2)之间存在边,符合团的条件,则继续深搜考虑 节点3 ,由于 节点3 与 节点1 之间不存在边,所以 3 不能加入团中,因此不能将 节点3 加入团中,再考虑节点 4 同理(与 节点2 不存在边),继续考虑节点5,符合团在条件,此时不能够继续搜索了,保存当前团 {1,2,5}。
上述过程搜索前,还需判断( cn+n-i>=bestn ),此时可以认为,即使剩下节点都考虑,最大团的节点数还是小于等于当前最大团在节点数。
② 回溯考虑其他情况,当不考虑 节点2 加入团中,往深处搜索,此时(cn+n-i<=bestn),无需再深搜考虑,其他情况同理。
#include<iostream>
#include<cstdio>
#include<string.h>
using namespace std;
const int maxn=101;
int a[maxn][maxn]; //邻接矩阵
int x[maxn];
int cn,bestn,n,m;
void backtrack(int i)
{if(i>n) // 搜索完所有节点 {bestn=cn;printf("%d\n",bestn);for(int j=1;j<=n;j++){/*if(x[j]==1)printf("%d ",j);*/printf("%d ",x[j]);}printf("\n");return;}int flag=1; // 判断是否与团中节点都相连for(int j=1;j<i;j++){if( x[j] && !a[j][i])//i与j不相连{flag=0;break;}}if(flag==1) //进入左子树{cn++;x[i]=1;backtrack(i+1);cn--;x[i]=0;}if(cn+n-i>bestn) //剪枝{backtrack(i+1);}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){ int u,v;scanf("%d%d",&u,&v);a[u][v]=1;a[v][u]=1;}backtrack(1);return 0;
}相关文章:

最大团问题--回溯法
一、相关定义 给定一个无向图 ,其中 V 是图的顶点集,E图的边集 完全图:如果无向图中的任何一对顶点之间都有边,这种无向图称为完全图 完全子图:给定无向图 ,如果 ,且对应任意 且 ,则…...

MBSE之简单介绍
MBSE之简单介绍 文章目录 MBSE之简单介绍1. What is MBSE?2. MBSE 最佳实践 1. What is MBSE? Model-Based Systems Engineering (MBSE), a.k.a. Model-Based Systems Development (MBSD), is a Systems Engineering process paradigm that emphasizes t…...

基于ODPS解析字段值为JSON的情况
最近在使用ODPS数据库,其中一个字段他是用JSON存储的,但是我是需要JSON字符串中的一个属性值就行,刚好ODPS中有一个函数可以用来使用! 使用案例 select GET_JSON_OBJECT({"id":1,"name":"xiaobai"},$.name);…...

CesiumJS【Basic】- #020 加载glb/gltf文件(Primitive方式)
文章目录 加载glb/gltf文件(Primitive方式)1 目标2 代码实现3 资源文件加载glb/gltf文件(Primitive方式) 1 目标 使用Primitive方式加载glb/gltf文件 2 代码实现 import * as Cesium from "cesium";const viewer = new Cesium.Viewer...

2024黑盾杯复现赛题MISC部分
一、一个logo 一张png图片,查看颜色通道即可发现flag 二、 学会Office 最好用联想自带的excel工具查看,我用WPS打开未解出题目 这里会发现有隐藏信息 隐藏信息为宏加密 。去百度了解宏加密后,发现有俩个宏,一个加密一个解密 执…...

Linux0.12内核源码解读(5)-head.s
大家好,我是呼噜噜,好久没有更新old linux了,本文接着上一篇文章图解CPU的实模式与保护模式,继续向着操作系统内核的世界前进,一起来看看heads.s as86 与GNU as 首先我们得了解一个事实,在Linux0.12内核源…...
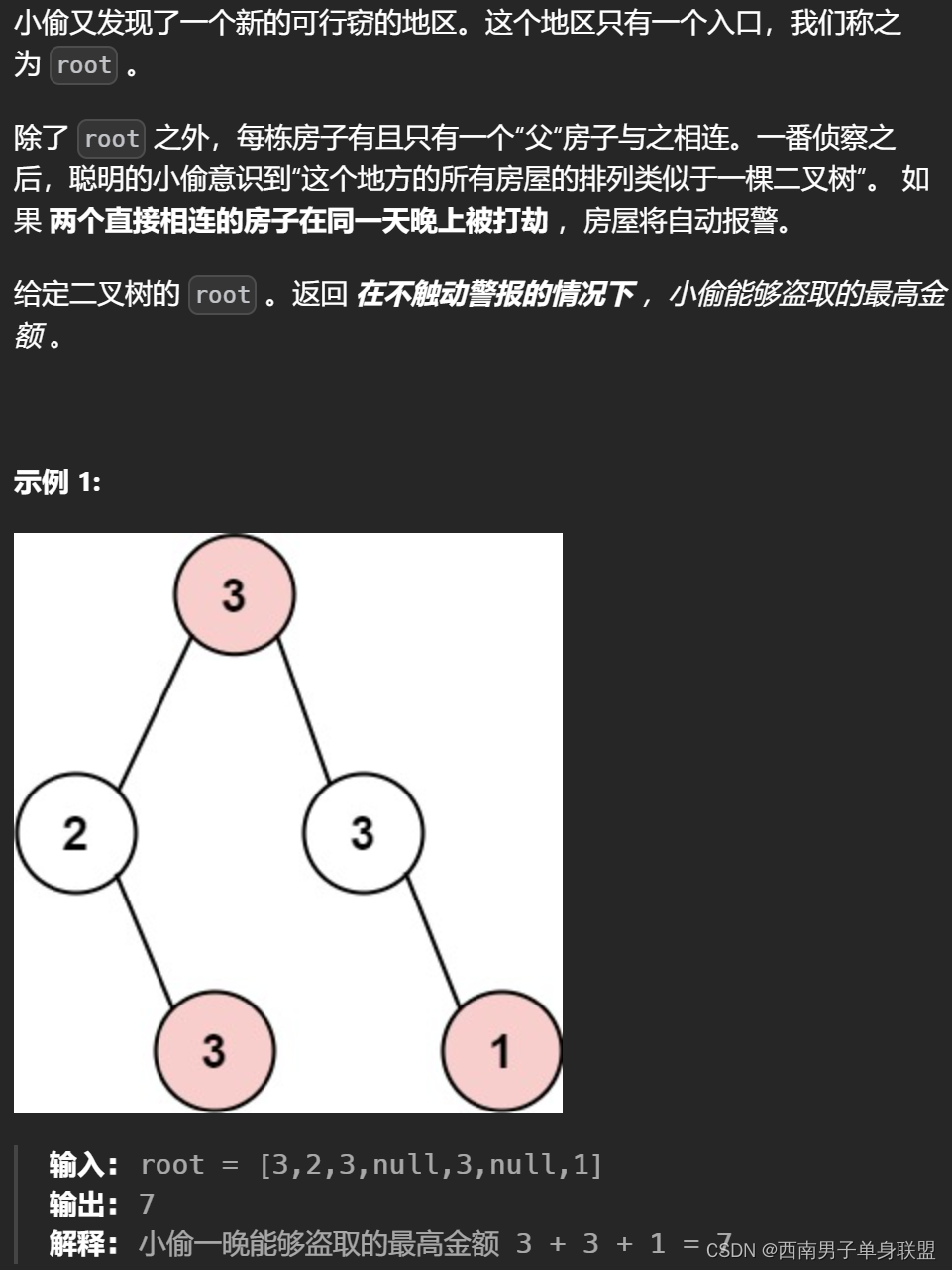
刷代码随想录有感(119):动态规划——打家劫舍III(树形dp)
题干: 代码: class Solution { public:vector<int>dp(TreeNode* cur){if(cur NULL)return vector<int>{0, 0};vector<int> left dp(cur -> left);vector<int> right dp(cur -> right);//偷int val1 cur -> val l…...

vivado CARRY_REMAP、CASCADE_HEIGHT
CARRY_REMAP opt_design-carry_remap选项可用于将单个carry*单元重新映射到LUT中 提高了布线的设计效果。使用-carry_remap选项时,仅 将单级进位链转换为LUT。CARRY_REMAP属性允许您 指定在优化过程中要转换的长度较大的进位链。 您可以使用控制任意长度的单个进位链…...
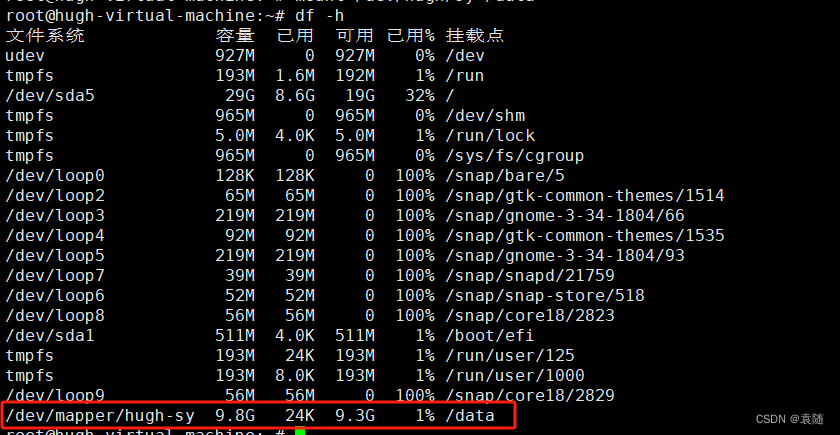
Ubuntu磁盘分区和挂载 虚拟机扩容 逻辑卷的创建和扩容保姆及教程
目录 1、VMware虚拟机Ubuntu20.04系统磁盘扩容 2、Linux的磁盘分区和挂载 3、创建逻辑卷和逻辑卷的扩容 1、VMware虚拟机Ubuntu20.04系统磁盘扩容 通过下图可以看出我们的根磁盘一共有20G的大小,现在我们把它扩容为30G 注:如果你的虚拟机有快照是无…...

【附精彩文章合辑】哈佛辍学小哥的创业经历【挑战英伟达!00 后哈佛辍学小哥研发史上最快 AI 芯片,比 H100 快 20 倍!】
前情提要 https://blog.csdn.net/weixin_42661676/article/details/140020491 哈佛辍学小哥的创业经历 一、背景与起步 这位哈佛辍学小哥,名为Chris Zhu,是一位华裔学生,他在2020年进入哈佛大学,攻读数学学士学位和计算机科学硕…...

Oracle CPU使用率过高问题处理
1.下载Process Explorer 2.打开Process Explorer,查看CPU使用情况最高的进程 3.双击该进程,查看详情 \ 4. 获取cpu使用最好的线程tid 5. 查询sql_id select sql_id from v$session where paddr in( select addr from v$process where spid in(1…...

pyqt的QWidgetList如何多选?如何按下Ctrl多选?
通过设置setSelectionMode(QAbstractItemView.MultiSelection),可以实现QWidgetList的多选。 但是上述结果不太符合我们需求。设置多选模式后,只需鼠标点击就可以选择多个条目。 我希望按下Ctrl键时才进行多选,仅鼠标单击的话,只进…...

【电路笔记】-MOSFET放大器
MOSFET放大器 文章目录 MOSFET放大器1、概述2、电路图3、电气特性3.1 ** I D = F ( V G S ) I_D=F(V_{GS}) ID=F(VGS)**特性3.2 I D = F ( V D S ) I_D=F(V_{DS}) ID=F(VDS)特性4、MOSFET放大器5、输入和输出电压6、电压增益7、总结1、概述 在前面的文章中,我们已经…...
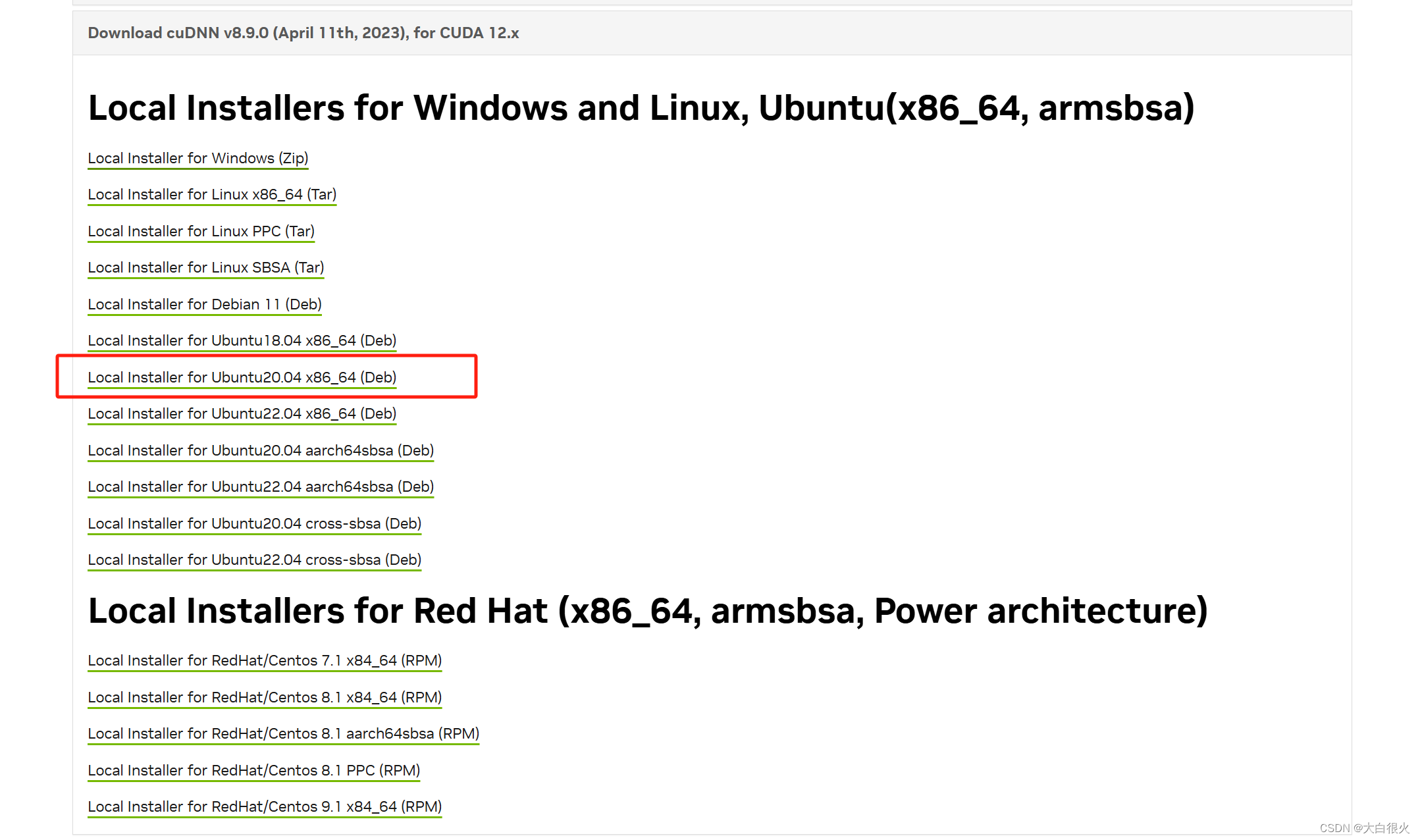
Ubuntu 20.04安装显卡驱动、CUDA、Pytorch(2024.06最新)
文章目录 一、安装显卡驱动1.1 查看显卡型号1.2 根据显卡型号选择驱动1.3 获取下载链接1.4 查看下载的显卡驱动安装文件1.5 更新软件列表和安装必要软件、依赖1.6 卸载原有驱动1.7 禁用默认驱动1.8 安装lightdm显示管理器1.9 停止显示服务器1.10 在文本界面中,禁用X…...

wpf 附加属性 RegisterAttached 内容属性
// // 摘要: // 选中时展示的元素 public static readonly DependencyProperty CheckedElementProperty DependencyProperty.RegisterAttached("CheckedElement", typeof(object), typeof(StatusSwitchElement), new PropertyMetadata((object)null…...
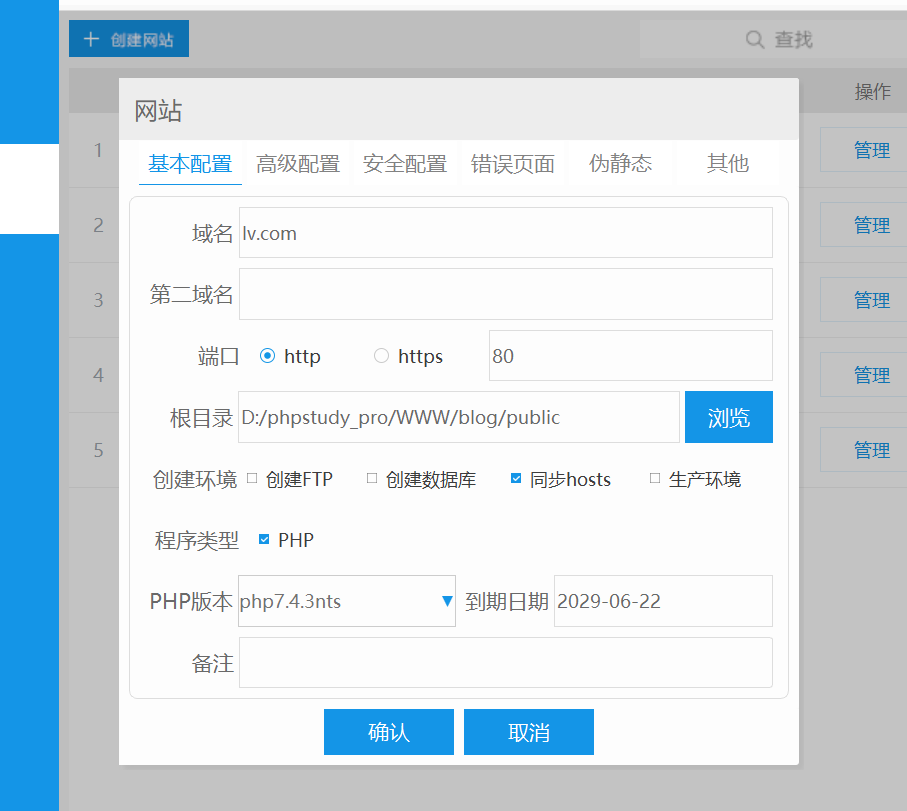
laravel8框架windows下安装运行
目录 1、安装前如果未安装先安装Composer 2、使用composer安装laravel8 3、使用内置服务器:8000 的命令去访问测试 4、使用本地环境运行phpstudy配置到public目录下 Laravel官网 Laravel 中文网 为 Web 工匠创造的 PHP 框架 安装 | 入门指南 |《Laravel 8 中文文档 8.x…...

如何快速判断IP被墙
IP被墙是指IP部分地区或者运营商无法被正常进行访问的一个情况。 被墙的原因有很多种不一一列举,由于被墙的时间短的为按周按月计算,时间长的则为按年计算,所以一般这种情况下只能选择更换IP。 检查办法: 第一,确认IP…...

vitest-前端单元测试
Vitest是一个轻量级、快速且功能强大的测试框架,特别适用于Vite项目,但也可以与其他前端项目(如使用webpack构建的项目)集成使用。Vitest提供极速的测试体验,并包含一系列用于编写和组织测试用例的API,如de…...

Redis 7.x 系列【9】数据类型之自动排重集合(Set)
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 前言2. 常用命令2.1 SADD2.2 SCARD2.3 SISMEMBER2.4 SREM2.5 SSCAN2.6 SDIFF2.7 SU…...

【LeetCode】每日一题:反转链表
题解思路 循环的方法需要注意prev应该是None开始,然后到结束的时候prev是tail,递归的思路很难绕过弯来,主要在于很难想清楚为什么可以返回尾节点,需要多做递归题,以及递归过程中,可以不使用尾节点来找当前…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
