最小生成树模型
文章目录
- 题单
- 最小生成树模型
- 1.[最短网络(prim)](https://www.acwing.com/problem/content/1142/)
- 2. [局域网(kruskul)](https://www.acwing.com/problem/content/1143/)
- 3. [繁忙的都市](https://www.acwing.com/problem/content/1144/)
- 4. [ 联络员 ](https://www.acwing.com/problem/content/1145/)
- 5. [连接格点 ](https://www.acwing.com/problem/content/1146/)
题单
最小生成树模型
1.最短网络(prim)
纯裸的一道prim模版题
和dijkstra区别:d数组记录的是一个点到生成树的最小距离
#include<bits/stdc++.h>using namespace std;
int n;
const int N=110,INF=0x3f3f3f3f;
int g[N][N],st[N],d[N];
int res;void prim(){memset(d,0x3f,sizeof d);d[1]=0;for(int i=1;i<=n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||d[t]>d[j])){t=j;}}res+=d[t];st[t]=1;for(int j=1;j<=n;j++) d[j]=min(d[j],g[t][j]);}
}signed main(){cin>>n;memset(g,0x3f,sizeof g);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>g[i][j];}}prim();cout<<res<<endl;return 0;
}
2. 局域网(kruskul)
纯裸的kruskul算法
#include<bits/stdc++.h>using namespace std;
int n,k;
const int N=110,M=210;
int fa[N];int find(int x){if(x!=fa[x]) return x=find(fa[x]);return fa[x];
}struct edges{int x,y,z;bool operator<(const edges& M)const{return z<M.z;}
}es[N];signed main(){cin>>n>>k;for(int i=1;i<=n;i++) fa[i]=i;for(int i=0;i<k;i++){int x,y,z;cin>>x>>y>>z;es[i]={x,y,z};}sort(es,es+k);int res=0;for(int i=0;i<k;i++){int a=find(es[i].x),b=find(es[i].y),c=es[i].z;if(a!=b){fa[a]=b;}else{res+=c;}}cout<<res<<endl;return 0;
}
3. 繁忙的都市
思考:
- 题目大意就是要一个最长边最小的最小生成树
- 根据kruskull本身就需要给边排序的特性,直接按序取直到形成一颗生成树
- 这里的最小生成树和传统的权值之和最小的生成树不一样
#include<bits/stdc++.h>using namespace std;
int n,m;
const int N=310,M=8e3+10;
int fa[N];struct edge{int x,y,z;bool operator< (const edge& M)const{return z<M.z;}
}edges[M];int find(int x){if(x!=fa[x]) x=find(fa[x]);return fa[x];
}signed main(){cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;edges[i]={x,y,z};}sort(edges,edges+m);int res;for(int i=0;i<m;i++){int a=find(edges[i].x),b=find(edges[i].y),c=edges[i].z;if(a!=b){fa[a]=b;res=c;}}cout<<n-1<<' '<<res<<endl;return 0;
}4. 联络员
第一眼:
- 根据线路分类:可以选择的路 以及 必须存在的路
- 也就是已知某些边的存在,找到剩下的边,使生成树权值最小(其实不确定还是不是求一颗生成树,但一定要满足每个点都能到,且选择的权值最小
- 那就直接kruskal算法
//一遍ac
#include<bits/stdc++.h>using namespace std;
const int N=2e3+10,M=1e4+10;
int fa[N];
int n,m;struct edge{int p,x,y,z;bool operator<(const edge& M)const{if(p==M.p){return z<M.z;}return p>M.p;}
}edges[M];int find(int x){if(x!=fa[x]) return x=find(fa[x]);return fa[x];
}signed main(){cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;int res=0;for(int i=0;i<m;i++){int p,x,y,z;cin>>p>>x>>y>>z;if(p==1){int a=find(x),b=find(y);fa[a]=b;res+=z;}edges[i]={p,x,y,z};}sort(edges,edges+m);for(int i=0;i<m;i++){int a=find(edges[i].x),b=find(edges[i].y),c=edges[i].z;if(a!=b){fa[a]=b;res+=c;}}cout<<res<<endl;return 0;
}
5. 连接格点
还是在已有连线的基础上找到权值之和最小生成树
处理点阵
- (1)把二维压成一维
- (2) 离散化
//第一版代码tle了#include<bits/stdc++.h>using namespace std;
int n,m;
const int N=1e3+10;
int fa[N*N],g[N][N];
int cnt=0;struct edge{int x,y,z;bool operator<(const edge& M)const{return z<M.z;}}edges[2*N*N];int find(int x){if(x!=fa[x]) x=find(fa[x]);return fa[x];
}signed main(){cin>>n>>m;for(int i=1;i<=n*m;i++) fa[i]=i;int x,y,xx,yy;int t=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){g[i][j]=++t;if(i+1<=n){edges[cnt++]={t,t+m,1};}if(j+1<=m)edges[cnt++]={t,t+1,2};}}while(cin>>x>>y>>xx>>yy){int a=find(g[x][y]),b=find(g[xx][yy]);if(a!=b){fa[a]=b;}}sort(edges,edges+cnt);int res=0;for(int i=0;i<cnt;i++){int a=find(edges[i].x),b=find(edges[i].y),c=edges[i].z;if(a!=b){fa[a]=b;res+=c;}}cout<<res<<endl;return 0;
}
边权为正才有最小生成树
小tips:
- 先建纵向边再建横向边,可以省去一步排序过程。
#include<bits/stdc++.h>using namespace std;
int n,m;
const int N=1e3+10;
int fa[N*N],g[N][N];
int cnt;struct edge{int x,y,z;}edges[2*N*N];int find(int x){if(x!=fa[x]) fa[x]=find(fa[x]);//这一步是路径压缩return fa[x];
}void get_edges(){int dx[]={-1,0,1,0},dy[]={0,1,0,-1},dw[]={1,2,1,2};for(int z=0;z<2;z++){for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int u=0;u<4;u++){if(u%2==z){int x=i+dx[u],y=j+dy[u],w=dw[u];if(x&&x<=n&&y&&y<=m){int a=g[i][j],b=g[x][y];if(a<b) edges[cnt++]={a,b,w};}}}}}}
}signed main(){cin>>n>>m;for(int i=1;i<=n*m;i++) fa[i]=i;int x,y,xx,yy;int t=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){g[i][j]=++t;}}while(cin>>x>>y>>xx>>yy){int a=find(g[x][y]),b=find(g[xx][yy]);//if(a!=b){// fa[a]=b;//}fa[a]=b;}get_edges();int res=0;for(int i=0;i<cnt;i++){int a=find(edges[i].x),b=find(edges[i].y),c=edges[i].z;if(a!=b){fa[a]=b;res+=c;}}cout<<res<<endl;return 0;
}
相关文章:

最小生成树模型
文章目录 题单最小生成树模型1.[最短网络(prim)](https://www.acwing.com/problem/content/1142/)2. [局域网(kruskul)](https://www.acwing.com/problem/content/1143/)3. [繁忙的都市](https://www.acwing.com/problem/content/1144/)4. [ 联络员 ](https://www.acwing.com/p…...

基于盲信号处理的声音分离-基于改进的信息最大化的ICA算法
基于信息最大化的ICA算法的主要依据是使输入端与输出端的互信息达到最大,且输出各个分量之间的相关性最小化,即输出各个分量之间互信息量最小化,其算法的系统框图如图所示。 基于信息最大化的ICA算法的主要依据是使输入端与输出端的互信息达到…...

如何在Qt Designer中管理QSplitter
问题描述 当按下按钮时,我希望弹出一个对话框,用户可以在其中选择内容并最终按下 ‘Ok’ 按钮。我想在这个对话框中放置一个 QSplitter,左侧面板将显示树状结构,右侧将显示其他内容。如何正确实现这一点? 从 Qt 的示…...

关于新零售的一些思考
本文作为2024上半年大量输入之后的核心思考之一。工作到一定阶段之后,思考的重要性越来越高,后续会把自己的个人思考记录在这个新系列《施展爱思考》。背景是上半年面临业务转型从电商到新零售,本文是相关大量输入之后的思考,对新…...

C++初学者指南-2.输入和输出---从输入流错误中恢复
C初学者指南-2.输入和输出—从输入流错误中恢复 文章目录 C初学者指南-2.输入和输出---从输入流错误中恢复怎么了?解决方案:出错后重置输入流 怎么了? 示例:连续输入 int main () {cout << "i? ";int i 0;cin…...

毫秒级响应!清科优能应用 TDengine 建设虚拟电厂运营管理平台
小T导读:在清科优能的虚拟电厂运营管理平台建设中,项目初期预计涉及约一万台设备、总数据采集量达数十万,在数据库选择上,其希望能支持至少两千台设备的并发数据处理。本文介绍了清科优能的数据库选型经验以及最终应用效果&#x…...

【Ubuntu noble】apt 无法安装软件 Unable to locate package vim
宿主机以及 docker 无法定位软件包 将 /etc/apt/sources.list.d/ubuntu.sources 修改为以下内容(主要是 Suites 字段增加了noble noble-updates) Types: deb URIs: http://archive.ubuntu.com/ubuntu/ Suites: noble noble-updates noble-backports Com…...
Instagram APIj接口——快速获取Ins帖子媒体内容下载链接
一、引言 在社交媒体蓬勃发展的今天,Instagram已成为用户分享照片、视频和精彩瞬间的首选平台。然而,对于很多用户来说,想要保存或分享Instagram上的精彩内容却常常遇到困扰。为了解决这个问题,我们精心打造了一款全新的Instagra…...

Java基础(四)——字符串、StringBuffer、StringBuilder、StringJoiner
个人简介 👀个人主页: 前端杂货铺 ⚡开源项目: rich-vue3 (基于 Vue3 TS Pinia Element Plus Spring全家桶 MySQL) 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 …...

吐血推荐!3款视频生成工具,全部国产,都免费
AI视频大模型的爆发,让创作爆款视频不再是专业人士的能力。 今天二师兄给大家推荐3款免费的视频生成工具。 01 可灵 推荐指数 : 五颗星 先看效果 可灵大模型测试 可灵大模型是快手AI团队自主研发的视频生成大模型,具备强大的视频创作能力&a…...

【Web3】Web3.js 启动!并解决Web3 is not a constructor报错
苏泽 大家好 这里是苏泽 一个钟爱区块链技术的后端开发者 本篇专栏 ←持续记录本人自学智能合约学习笔记和经验总结 如果喜欢拜托三连支持~ 本节教大家如何启动Web3.js 目录 Web3 启动! 于是很愉快的报错 创建实例! 出来了 Web3:模块…...

算法训练营第六十七天 | 卡码网110 字符串接龙、卡码网105 有向图的完全可达性、卡码网106 岛屿的周长
卡码网110 字符串接龙 这题一开始用的邻接表dfs,不幸超时 #include <iostream> #include <list> #include <string> #include <vector> using namespace std;int minLen 501;bool count(string a, string b) {int num 0;for (int i 0; …...

搭建 MySQL MHA
搭建 MySQL MHA 搭建 MySQL MHA实验拓扑图实验环境实验思路MHA架构故障模拟 实验部署数据库安装主从复制部署时间同步主服务器配置从服务器配置创建链接 MHA搭建安装依赖的环境安装 node 组件安装 manager 组件配置无密码认证在 manager 节点上配置 MHA管理 mysql 节点服务器创…...

python中的线程与进程
一、线程与进程 在计算机科学中,理解线程和进程的区别是重要的基础知识。这些概念对于多任务操作和并发编程尤为关键。下面将详细介绍线程与进程的区别、特点和各自的使用场景。 1.1 进程(Process) 进程是操作系统分配资源的基本单位。每个进…...

网络安全筑基篇——反序列化漏洞
目录 序列化是什么? 反序列化又是什么? 反序列化漏洞的危害 代码样例 常见的魔术方法 修复方式有哪些? 常见的反序列化漏洞 Shiro反序列化漏洞 Fastjson反序列化漏洞 序列化是什么? 将实例化对象转换成字节流的过程 反序…...
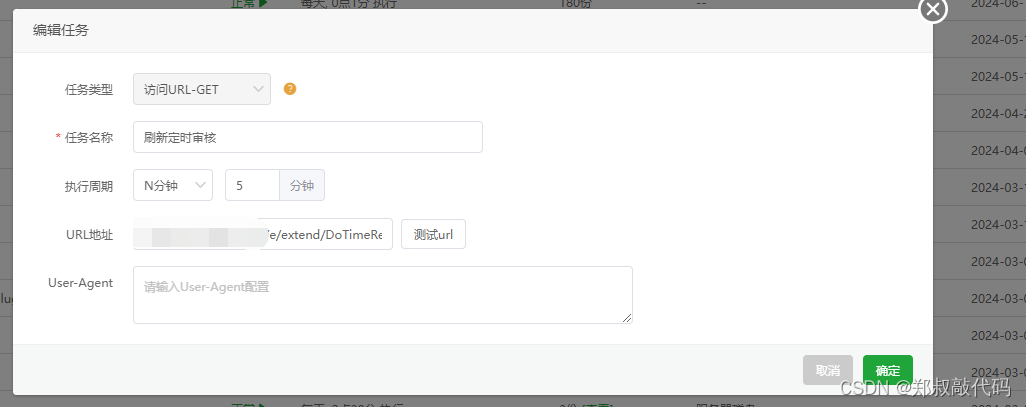
帝国cms定时审核并更新的方法
比如你网站采集了成千上万篇文章,不可能一下子全部放出来的,所以为了模拟人工发布,那么就需要定时审核发布文章内容,本文内容核心解决了更加个性化的逼真模拟人工更新网站内容。 第一:首先要满足你的表中有未审核的数据…...
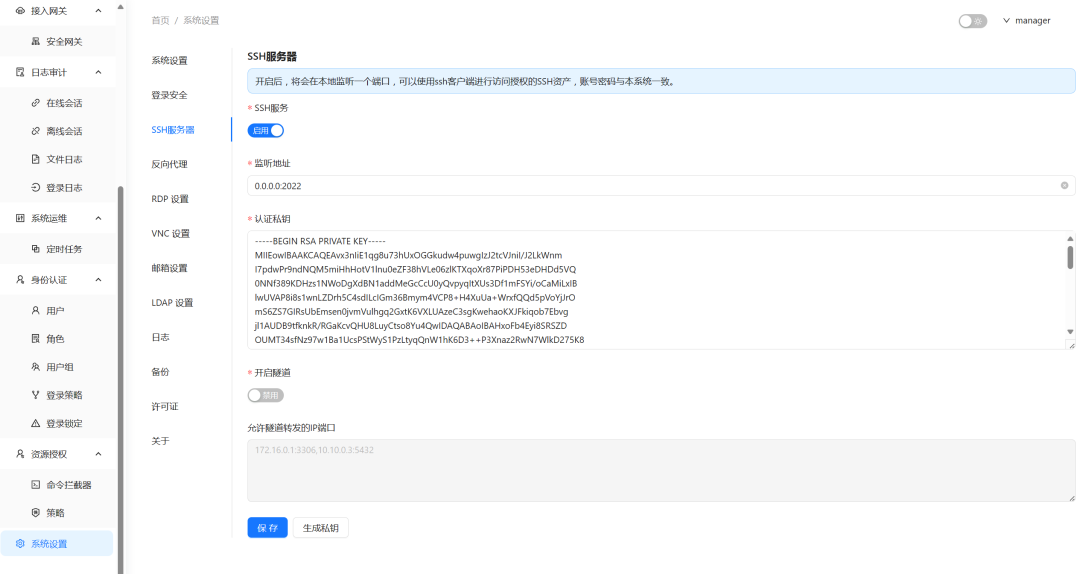
一个简单好用安全的开源交互审计系统,支持SSH,Telnet,Kubernetes协议
前言 在当今的企业网络环境中,远程访问和交互审计成为了保障网络安-全的重要组成部分。然而,现有的解-决方案往往存在一些痛点,如复杂的配置、有限的协议支持、以及审计功能的不足。这些问题不仅增加了IT管理员的负担,也为企业的…...

使用Spring Boot和WebSocket实现实时通信
使用Spring Boot和WebSocket实现实时通信 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中使用WebSocket实现实时通信&am…...
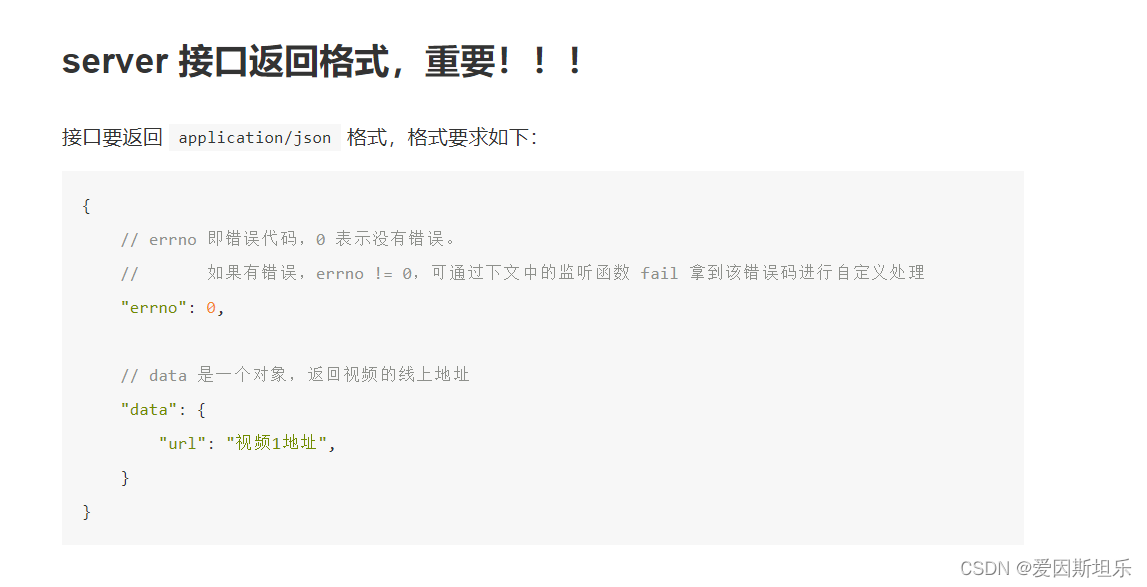
【Vue】集成富文本编辑器
这文章使用的是wangeditor插件,官网地址:wangEditor,这个比较简单 安装 npm i wangeditor --save 使用 <div id"editor"></div>import E from "wangeditor"const editor new E("#editor") e…...

【论文阅读】--Popup-Plots: Warping Temporal Data Visualization
弹出图:扭曲时态数据可视化 摘要1 引言2 相关工作3 弹出图3.1 椭球模型3.1.1 水平轨迹3.1.2 垂直轨迹3.1.3 组合轨迹 3.2 视觉映射与交互 4 实施5 结果6 评估7 讨论8 结论和未来工作致谢参考文献 期刊: IEEE Trans. Vis. Comput. Graph.(发表日期: 2019&…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
