当前位置： 首页 > news >正文

MATLAB实现层次分析法AHP及案例分析

news 2025/12/15 23:52:55

层次分析法（Analytic Hierarchy Process, AHP）

1 模型背景

美国运筹学家匹兹堡大学教授Saaty在20世纪70年代初提出的一种层次权重决策分析方法。
层次分析法（Analytic Hierarchy Process, AHP）是一种定性和定量分析相结合的决策分析方法。
特点：用较少的定量信息使决策的思维过程数学化。

2 基本步骤

层次分析法进行建模，大致分为以下五步：

  • 分析系统中各因素之间的关系，建立系统的递阶层次结构（目标层、准则层、方案层）。
    在这里插入图片描述

  • 对于同一层次的个元素关于上一层次中某一准则的重要性两两比较，构造两两比较矩阵（判断矩阵）。

  • 计算单排序权向量，并进行一致性检验（检验通过权重才能用）。
    对每个成对比较矩阵计算最大特征值及其对应的特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量(归一化后)即为权向量；若不通过，需要重新构造成对比较矩阵。

  • 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过权重才能用࿰

相关文章：

MATLAB实现层次分析法AHP及案例分析

层次分析法（Analytic Hierarchy Process, AHP） 1 模型背景 美国运筹学家匹兹堡大学教授Saaty在20世纪70年代初提出的一种层次权重决策分析方法。 层次分析法（Analytic Hierarchy Process, AHP）是一种定性和定量分析相结合的决策分析方法。 特点：用较少的定量信息使决策的…...

编程日记 2023/3/12 2:56:38

Vue 3.0 TypeScript支持

Vue CLI 提供内置的 TypeScript 工具支持。 #NPM 包中的官方声明 随着应用的增长，静态类型系统可以帮助防止许多潜在的运行时错误，这就是为什么 Vue 3 是用 TypeScript 编写的。这意味着在 Vue 中使用 TypeScript 不需要任何其他工具——它具有一流的公…...

编程日记 2023/3/12 2:55:33

STM8S系列基于IAR标准外设printf输出demo

STM8S系列基于IAR标准外设printf输出demo📌STM8S/A标准外设库（库版本V2.3.1）📍官网标准外设库：https://www.st.com/zh/embedded-software/stsw-stm8069.html ⛳注意事项 🚩在内存空间比较有限的情况下&am…...

编程日记 2023/3/12 2:54:29

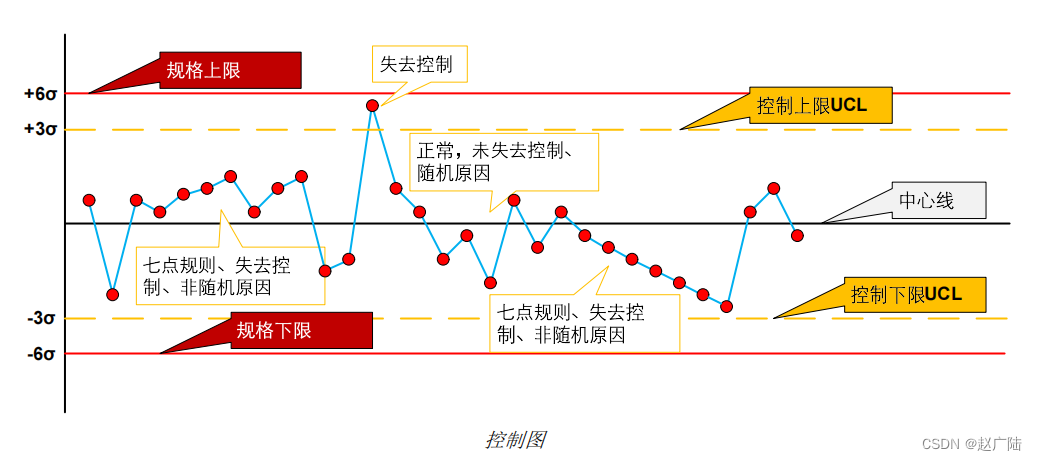
PMP项目管理项目质量管理

目录1 项目质量管理概述2 规划质量管理3 管理质量4 控制质量1 项目质量管理概述 项目质量管理包括把组织的质量政策应用于规则、管理、控制项目和产品质量要求，以满足相关方目标的各个过程。项目质量管理还将以组织的名义支持过程的持续改进活动。 核心概念 质量是…...

编程日记 2023/3/12 2:53:26

前缀和总结

前缀和是一个常用的算法技巧，通常用于求解数组或序列的区间和。 具体来说，假设有一个长度为n的数组a，我们可以预处理出一个长度为n+1的前缀和数组s，其中s[i]表示原数组a前i个元素的和，即： s[i] = a[0] + a[1] + ... + a[i-1] 这样一来，对于任意的区间[l, r]，我们可以…...

编程日记 2023/3/12 2:52:21

0109二分图-无向图-数据结构和算法(Java)

文章目录1 概念2 API3 分析和实现4 测试5 总结后记1 概念 二分图是一种能将所有结点分为两部分的图，其中图的每条边所连接的两个顶点都分别属于不同的部分。 2 API public classBipartiteBipartite(Graph G)预处理函数public booleanisBipartitle()是否是二分图pub…...

编程日记 2023/3/12 2:51:18

计算机网络题库---选择题刷题训练（100多道精品）

第一章 概述 1.下列四项内容中，不属于Internet（因特网）基本功能是___D_____。 A.电子邮件 B.文件传输 C.远程登录 D.实时监测控制 2.Internet是建立在____C_____协议集上的国际互联网络。 A.IPX B.NetBEUI C.TCP/IP …...

编程日记 2023/3/12 2:50:15

16、字符串生成器

目录 （1）append()方法 （2）insert(int offset, arg)方法 （3）delete(int start , int end)方法 创建成功的字符串对象，其长度是固定的，内容不能被改变和编译。虽然使用“”可以达到…...

编程日记 2023/3/12 2:49:12

docker基本命令-容器

容器 基本概念 镜像（Image）和容器（Container）的关系，就像是面向对象程序设计中的 类 和 实例 一样，镜像是静态的定义，容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等。 容…...

编程日记 2023/3/12 2:46:58

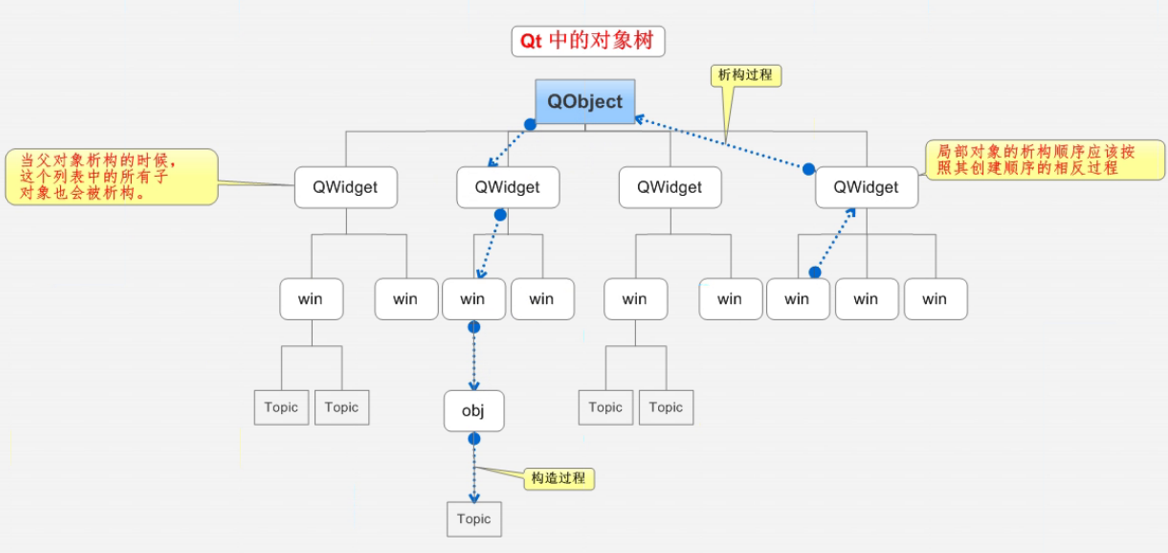
QT入门基础(一)

文章目录零.Qt背景1.什么是Qt2.Qt的发展史3.Qt的优势4.Qt应用一.第一个Qt程序0.项目创建1.main函数文件2.类头文件3.pro文件4.qt命名规范二.Qt按钮1.按钮创建和父子关系2.按钮常用api3.Qt窗口坐标体系4.对象树模型零.Qt背景 1.什么是Qt Qt是一个跨平台的C图形用户界面应用程序…...

编程日记 2023/3/12 2:45:54

WattOS：一个稳又快的轻量级 Linux 发行版

导读Linux 领域里的每个人不是听说过就是使用过某个轻量级的 Linux 发行版。大家都知道我们不断追求的是：占用内存少，配置资源要求低，包含一个轻量级的桌面环境（或者窗口管理器），并且提供和其他发行版相似的…...

编程日记 2023/3/12 2:44:51

Java调用Python脚本：轻松实现两种语言的互操作性

Java和Python都是非常流行的编程语言，它们都有自己的优点，但也有自己的局限性。在编写应用程序时，我们可能需要使用两种语言来共同完成一项任务。在这种情况下，Java需要调用Python脚本来解决某些问题，同时利用Java和Py…...

编程日记 2023/3/12 2:43:46

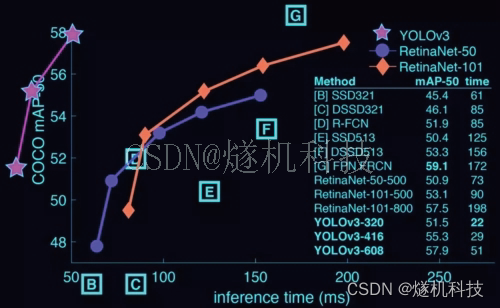
未系安全带识别系统 yolo

未系安全带识别系统通过pythonyolo智能视频分析技术，未系安全带识别算法对画面中高空作业人员未系安全带行为进行监测，未系安全带识别算法监测到人员未穿戴安全带时，立即通知后台人员及时处理触发告警。Yolo算法采用一个单独的CNN模型实现end…...

编程日记 2023/3/12 2:42:42

（七十六）大白话MySQL是如何根据成本优化选择执行计划的？（上）

之前已经给大家讲解清楚了 MySQL 在执行单表查询时候的一些执行计划，比如说const、ref、range、index、all之类的，也讲了多表关联的时候是如何执行的，本质其实就是先查一个驱动表，接着根据连接条件去被驱动表里循环查询&#xff0…...

编程日记 2023/3/12 2:41:38

DSRC技术

DSRC(Dedicated Short Range Communication)专用短程通信 定位 是V2X领域存在的两大通信技术之一（另一个为LTE-V2X）。 所属技术路线 与这两大技术相对应，是V2X无线通信技术的两大技术路线： IEEE 802.11p 本是04年指定的一个通…...

编程日记 2023/3/12 2:40:34

_面经问题_

一、Java编程语言 Java语言有哪些特点? JVM vs JDK vs JRE 什么是字节码? 采用字节码的好处是什么? 为什么不全部使用AOT呢? 为什么说Java语言"编译与解释并存"? Oracle JDK vs OpenJDK Java和C的区别? 注释有哪几种形式? 标识符和关键字的区别是什么? Jav…...

编程日记 2023/3/12 2:39:32

刷题记录(2023.3.6 - 2023.3.11)

我很喜欢这周的感觉，前两道题对着 wp 简略复现了一下，由于以前都是自己学习，对一些稍微多、稍微难的题都会马上避开，笨小孩逃避太久了，有些事逃不掉，总得面对，开始往往很难，多花点时…...

编程日记 2023/3/12 2:38:26

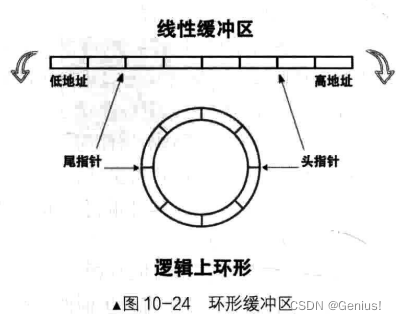
14 Day：同步锁与操作系统输入输出

前言：在上一期的线程章节中，我们的线程输出貌似有大问题，今天我们便要来学习同步锁来解决这个问题，同时再次基础上拿下键盘输入，实现操作系统的输入和输出。从今天开始我们的操作系统不在是一块“看板”了！…...

编程日记 2023/3/12 2:37:21

Gradle 的下载安装教程

Gradle 8.0.1 下载安装教程笔者的环境： Java 17.0.1 Gradle 8.0.1 Windows 10 教育版 64位 在继续阅读本教程之前，需要先完成 JDK 的安装。JDK 需要选择 8 及以上的版本。关于 JDK 的安装，可见笔者的另一篇博客： Java 的下载安…...

编程日记 2023/3/12 2:36:17

「Python 基础」常用模块

文章目录1. 内建模块datetimecollectionsnamedtuple()dequedefaultdictOrderedDictChainMapCounterbase64structhashlib摘要算法摘要的应用hmacitertoolscontextlib\_\_enter\_\_ 和 \_\_exit\_\_contextmanagerclosingurllibGETPOSTHandlerXMLDOMSAXHTMLParser2. 第三方模块Pi…...

编程日记 2023/3/12 2:35:14

OkHttp 中实现断点续传 demo

在 OkHttp 中实现断点续传主要通过以下步骤完成，核心是利用 HTTP 协议的 Range 请求头指定下载范围： 实现原理 Range 请求头：向服务器请求文件的特定字节范围（如 Range: bytes1024-） 本地文件记录：保存已…...

编程新知 2025/12/12 0:56:22

Cinnamon修改面板小工具图标

Cinnamon开始菜单-CSDN博客 设置模块都是做好的，比GNOME简单得多！ 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

编程新知 2025/12/14 17:38:32

【Java_EE】Spring MVC

目录 Spring Web MVC ​编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 ​编辑参数重命名 RequestParam ​编辑​编辑传递集合 RequestParam 传递JSON数据 ​编辑RequestBody ​…...

编程新知 2025/12/12 6:00:18

NLP学习路线图（二十三）：长短期记忆网络（LSTM）

在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...

编程新知 2025/12/11 21:25:46

让AI看见世界：MCP协议与服务器的工作原理

让AI看见世界：MCP协议与服务器的工作原理 MCP（Model Context Protocol）是一种创新的通信协议，旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天，MCP正成为连接AI与现实世界的重要桥梁。…...

编程新知 2025/12/12 7:41:41

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

编程新知 2025/9/17 22:26:02

JVM虚拟机：内存结构、垃圾回收、性能优化

1、JVM虚拟机的简介 Java 虚拟机（Java Virtual Machine 简称：JVM）是运行所有 Java 程序的抽象计算机，是 Java 语言的运行环境，实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息，使得 Java 程序只需生成在 JVM 上运行的目标代码（字节码），就可以…...

编程新知 2025/12/15 2:10:04

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要： 近期，在使用较新版本的OpenSSH客户端连接老旧SSH服务器时，会遇到 "no matching key exchange method found"​, "n…...

编程新知 2025/9/29 4:00:38

android13 app的触摸问题定位分析流程

一、知识点 一般来说，触摸问题都是app层面出问题，我们可以在ViewRootImpl.java添加log的方式定位；如果是touchableRegion的计算问题，就会相对比较麻烦了，需要通过adb shell dumpsys input > input.log指令，且通过打印堆栈的方式，逐步定位问题，并找到修改方案。 问题…...

编程新知 2025/12/2 1:15:53

MySQL的pymysql操作

本章是MySQL的最后一章，MySQL到此完结，下一站Hadoop！！！ 这章很简单，完整代码在最后，详细讲解之前python课程里面也有，感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

编程新知 2025/12/8 16:58:20