【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】卷积
卷积经常用在信号处理中,用于计算信号的延迟累积。假设一个信号发射器每个时刻 t t t产生一个信号 x t x_t xt,其信息的衰减率为 w k w_k wk,即在 k − 1 k-1 k−1个时间步长后,信息为原来的 w k w_k wk倍,时刻 t t t收到的信号 y t y_t yt为当前时刻产生的信息 x t x_t xt和以前时刻延迟信息 w t − 1 x t − 1 + ⋯ + w 1 x 1 w_{t-1}x_{t-1}+\cdots+w_1x_1 wt−1xt−1+⋯+w1x1的叠加。假设 w 1 = 1 , w 2 = 1 2 , w 3 = 1 4 w_1=1,w_2=\frac{1}{2},w_3=\frac{1}{4} w1=1,w2=21,w3=41也就是
x 1 y 1 = x 1 x 2 y 2 = x 2 + 1 2 x 1 x 3 y 3 = x 3 + 1 2 x 2 + 1 4 x 1 ⋮ ⋮ \begin{aligned} &x_1&y_1=x_1\\ &x_2&y_2=x_2+\frac{1}{2}x_1\\ &x_3&y_3=x_3+\frac{1}{2}x_2+\frac{1}{4}x_1\\ &\vdots&\vdots \end{aligned} x1x2x3⋮y1=x1y2=x2+21x1y3=x3+21x2+41x1⋮
因此,时刻 t t t(假设前面还有n个信号)收到的信号 y t y_t yt可以记作
y t = w 1 x t + w 2 x t − 1 + ⋯ + w n x t − n + 1 = ∑ k = 1 n w k x t − k + 1 \begin{aligned} y_t &=w_1x_t+w_2x_{t-1}+\cdots+w_nx_{t-n+1}\\ &=\sum_{k=1}^nw_kx_{t-k+1} \end{aligned} yt=w1xt+w2xt−1+⋯+wnxt−n+1=k=1∑nwkxt−k+1
其中 w k w_k wk叫做滤波器(filter) 或卷积核(convolution kernel)
定义
给定一个输入信号序列 x x x和滤波器 w w w,卷积输出为:
y t = ∑ k = 1 K w k x t − k + 1 y_t=\sum_{k=1}^Kw_kx_{t-k+1} yt=k=1∑Kwkxt−k+1
也可记作 y t = x ∗ w y_t=x\ast w yt=x∗w,其中 ∗ * ∗是卷积符号。要注意卷积核的序列顺序与输入信号序列顺序相反,在运算时需要将卷积核反转。

上图中,下面一行为输入序列 x x x,上面为输出序列 y y y,卷积核为 [ − 1 , 0 , 1 ] [-1,0,1] [−1,0,1],为了计算首先反转卷积核变为 [ 1 , 0 , − 1 ] [1,0,-1] [1,0,−1](或者从第三个开始往前计算,完成后再从开始的第三个再往后三个也就是第六个往前,以此类推),将反转后的卷积核在输入序列上平移得到输出序列。对于长度为 N N N的输入序列 x x x来说,若卷积核长度为 K K K,则输出序列 y y y长度为 N − K + 1 N-K+1 N−K+1
作用
近似微分
将输入序列 x = [ x t − 1 , x t , x t + 1 ] x=[x_{t-1},x_t,x_{t+1}] x=[xt−1,xt,xt+1]看作关于某时刻 t t t的函数,即 x ( t ) = x t x(t)=x_t x(t)=xt,根据一阶微分定义
x ′ ( t ) = x ( t + ϵ ) − x ( t − ϵ ) 2 ϵ x^\prime(t)=\frac{x(t+\epsilon)-x(t-\epsilon)}{2\epsilon} x′(t)=2ϵx(t+ϵ)−x(t−ϵ)
令 ϵ = 1 \epsilon=1 ϵ=1可得
x ′ ( t ) = x ( t + 1 ) − x ( t − 1 ) 2 = 1 2 x ( t + 1 ) + 0 × x t − 1 2 x ( t − 1 ) = x ∗ w \begin{aligned} x^\prime(t) &=\frac{x(t+1)-x(t-1)}{2}\\ &=\frac{1}{2}x(t+1)+0\times x_t-\frac{1}{2}x(t-1)\\ &=x\ast w \end{aligned} x′(t)=2x(t+1)−x(t−1)=21x(t+1)+0×xt−21x(t−1)=x∗w
其中 w = [ 1 2 , 0 , − 1 2 ] w=[\frac{1}{2},0,-\frac{1}{2}] w=[21,0,−21]。因此,当令卷积核 w = [ 1 2 , 0 , − 1 2 ] w=[\frac{1}{2},0,-\frac{1}{2}] w=[21,0,−21]时,可以近似信号序列的一阶微分
此外,根据泰勒公式
x ( t + ϵ ) = x ( t ) + x ′ ( t ) ϵ + x ′ ′ ( t ) 2 ! ϵ 2 + O ( ϵ 3 ) x(t+\epsilon)=x(t)+x^\prime(t)\epsilon+\frac{x^{\prime\prime}(t)}{2!}\epsilon^2+O(\epsilon^3) x(t+ϵ)=x(t)+x′(t)ϵ+2!x′′(t)ϵ2+O(ϵ3)
因此可得
x ( t + 1 ) = x ( t ) + x ′ ( t ) + x ′ ′ ( t ) 2 x ( t − 1 ) = x ( t ) − x ′ ( t ) + x ′ ′ ( t ) 2 \begin{aligned} x(t+1)=x(t)+x^\prime(t)+\frac{x^{\prime\prime}(t)}{2}\\ x(t-1)=x(t)-x^\prime(t)+\frac{x^{\prime\prime}(t)}{2} \end{aligned} x(t+1)=x(t)+x′(t)+2x′′(t)x(t−1)=x(t)−x′(t)+2x′′(t)
两式相加得
x ( t + 1 ) + x ( t − 1 ) = 2 x ( t ) + x ′ ′ ( t ) x ′ ′ = x ( t + 1 ) + x ( t − 1 ) − 2 x ( t ) = x ∗ w \begin{aligned} x(t+1)+x(t-1)&=2x(t)+x^{\prime\prime}(t)\\ x^{\prime\prime}&=x(t+1)+x(t-1)-2x(t)\\ &=x\ast w \end{aligned} x(t+1)+x(t−1)x′′=2x(t)+x′′(t)=x(t+1)+x(t−1)−2x(t)=x∗w
其中 w = [ 1 , − 2 , 1 ] w=[1,-2,1] w=[1,−2,1]。因此,当令卷积核 w = [ 1 , − 2 , 1 ] w=[1,-2,1] w=[1,−2,1]时,可以近似信号序列的二阶微分
低通滤波/高通滤波
- 高频信息:在信号序列中,局部数值变化剧烈的信息
- 低频信息:在信号序列中,局部数值变化缓慢的信息
对于一个窗口大小为 K K K的卷积核,只需要将滤波器中的每一项设置为 1 K \frac{1}{K} K1即可检测信号序列中的低频信息。

上图中 K = 3 K=3 K=3
一般来说,信号序列中的某个信息出现的频率越高,对应的阶数就越高。因此可以用二阶导数( w = [ 1 , − 2 , 1 ] w=[1,-2,1] w=[1,−2,1])的大小来表示其出现的频率。

对卷积进行扩展
为了更灵活的使用卷积,可以对卷积的过程进行扩展,引入滤波器的滑动步长(Stride) S S S和零填充(Padding) P P P
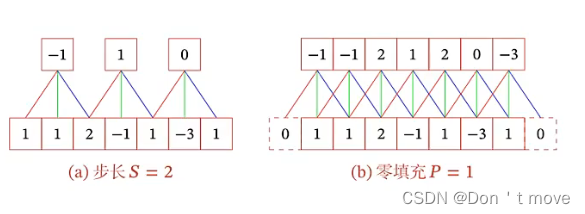
滑动步长是指卷积核在输入序列上每次平移的步长,一般默认滑动步长为1,也就是每次计算完输入序列上的一次卷积后,向前移动一个元素再进行卷积计算,通过增加步长可以减少输出序列的长度。
零填充是指在输入序列的两端各填充 P P P个0,这样做可以保证输入序列和输出序列长度相等。对于一个窗口大小为 K K K(一般为奇数)的卷积核来说,在输入序列两端各填充 K − 1 2 \frac{K-1}{2} 2K−1
若输入长度为 M M M,步长为 S S S,卷积核窗口大小为 K K K,零填充为 P P P,则输出长度为 M ′ = M − K + 2 P S + 1 M^\prime=\frac{M-K+2P}{S}+1 M′=SM−K+2P+1
卷积类型可以按照输出长度不同可以分为三类:
- 窄卷积:步长 S = 1 S=1 S=1,两端不补零( P = 0 P=0 P=0),输出长度为 M − K + 1 M-K+1 M−K+1
- 宽卷积:步长 S = 1 S=1 S=1,两端补零( P = K − 1 P=K-1 P=K−1),输出长度为 M + K − 1 M+K-1 M+K−1
- 等宽卷积:步长 S = 1 S=1 S=1,两端补零( P = K − 1 2 P=\frac{K-1}{2} P=2K−1),输出长度为 M M M
早期的文献中,卷积一般默认为窄卷积
目前的文献中,卷积一般默认为等宽卷积
二维卷积
输入序列扩展为二维,对这个二维输入序列进行卷积,一般用于图像处理。
给定图像 X ∈ R M × N X\in\mathbb{R}^{M\times N} X∈RM×N和一个滤波器 W ∈ R U × V W\in\mathbb{R}^{U\times V} W∈RU×V( U ≪ M , V ≪ N U\ll M,V\ll N U≪M,V≪N) ,其卷积为
Y = W ∗ X Y=W\ast X Y=W∗X
y i j = ∑ u = 1 U ∑ v = 1 V w u v x i − u + 1 , j − v + 1 y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{uv}x_{i-u+1, j-v+1} yij=u=1∑Uv=1∑Vwuvxi−u+1,j−v+1
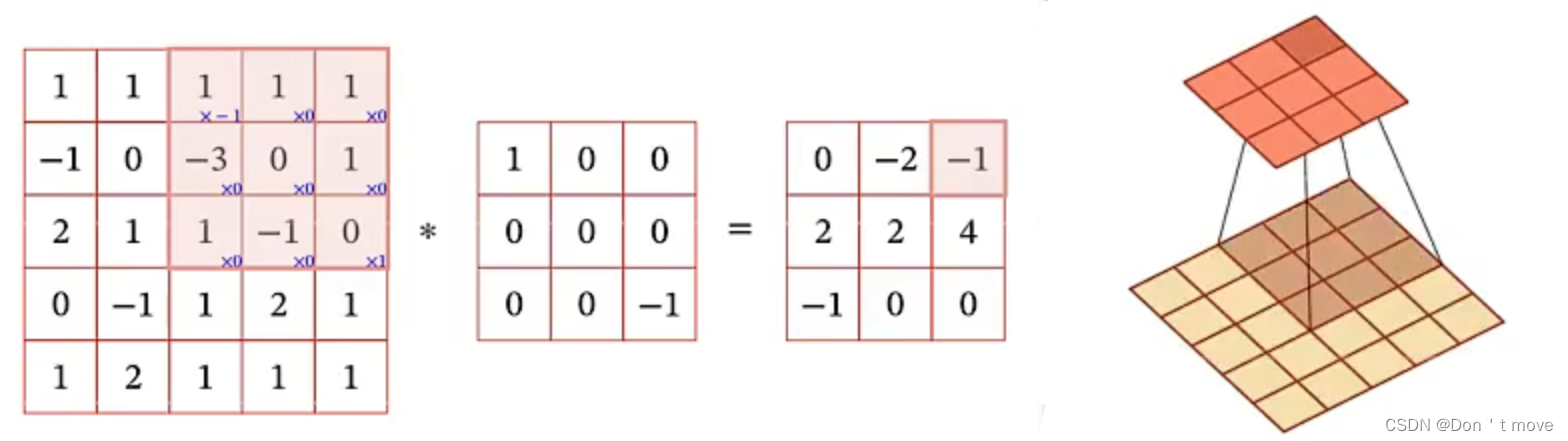
卷积核窗口在输入序列上进行滑动,可以计算出每个位置上的信号,最终得到输出。在计算时仍然要对卷积核进行反转。以上图为例,实际上是计算输入与反转后的卷积核的哈达玛积所有元素的和。
输入与输出大小与一维时规则相同,输出 y ∈ R ( M − U + 1 ) × ( N − V + 1 ) y\in\mathbb{R}^{(M-U+1)\times(N-V+1)} y∈R(M−U+1)×(N−V+1)。同样的也可以用滑动步长和零填充的方法来调整输出矩阵的大小:
-
对于步长为1,零填充0的输入序列,输出为 R ( M − U + 1 ) × ( N − V + 1 ) \mathbb{R}^{(M-U+1)\times(N-V+1)} R(M−U+1)×(N−V+1)
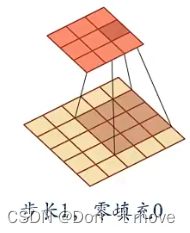
-
对于步长为2,零填充0的输入序列,输出为 R ( M − U 2 + 1 ) × ( N − V 2 + 1 ) \mathbb{R}^{(\frac{M-U}{2}+1)\times(\frac{N-V}{2}+1)} R(2M−U+1)×(2N−V+1)
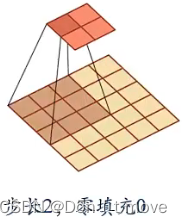
-
对于步长为1,零填充1的输入序列,输出为 R M × N \mathbb{R}^{M\times N} RM×N

-
对于步长为2,零填充1的输入序列,输出为 R ( M − U + 1 ) × ( N − V + 1 ) \mathbb{R}^{(M-U+1)\times(N-V+1)} R(M−U+1)×(N−V+1)
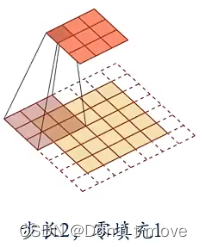
在图像处理中,可以利用卷积作为特征提取器,设计不同的卷积核来提取图像的不同特征。
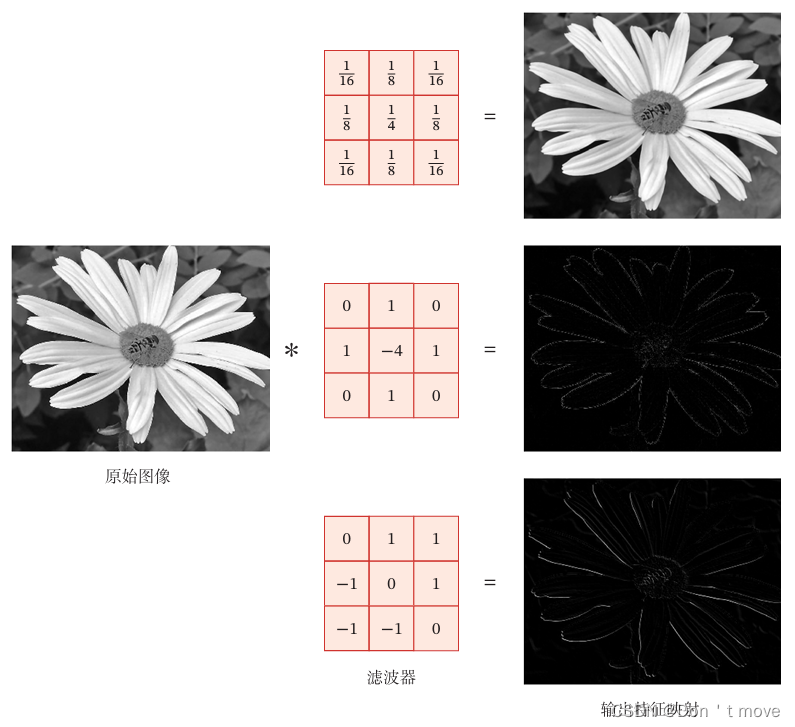
如上图,通过第一个卷积核(高斯卷积核)可以去除图像中的噪声(用周围点的信息平均中间不一样点的信息),使图像更加平滑;通过第二个卷积核,可以提取图像的边缘特征(上下左右信息的和减去中间信息,即提取图像中的高频信息);第三个卷积核可以提取图像对角线上的边缘特征(右上角图像信息减去左下角图像信息)
相关文章:

【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】卷积
卷积经常用在信号处理中,用于计算信号的延迟累积。假设一个信号发射器每个时刻 t t t产生一个信号 x t x_t xt,其信息的衰减率为 w k w_k wk,即在 k − 1 k-1 k−1个时间步长后,信息为原来的 w k w_k wk倍,时刻 …...

Trie字符串统计
Trie字符串统计 维护一个字符串集合,支持两种操作: I x 向集合中插入一个字符串 x;Q x 询问一个字符串在集合中出现了多少次。 共有 N个操作,所有输入的字符串总长度不超过 105,字符串仅包含小写英文字母。 输入格式…...

Kali Linux源
中科大 deb http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib deb-src http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib阿里云 deb http://mirrors.aliyun.com/kali kali-rolling main non-free contrib deb-src http://mirrors.…...
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统 一 文档简介二 平台构建2.1 使用平台2.2 百度智能云2.2.1 物联网核心套件2.2.2 在线语音合成 2.3 playback语音数据准备与烧录2.4 开机语音准备与添加2.5 唤醒词识别词命令准备与添加 三 代码准备3.1 sln-local/2-iot 代码…...
国标GB28181视频汇聚平台EasyCVR设备展示数量和显示条数不符的原因排查与解决
国标GB28181/GA/T1400协议/安防综合管理系统EasyCVR视频汇聚平台能在复杂的网络环境中,将前端设备统一集中接入与汇聚管理。智慧安防/视频存储/视频监控/视频汇聚EasyCVR平台可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级…...

FastAPI教程I
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial 第一步 import uvicorn from fastapi import FastAPIapp FastAPI()app.get("/") async def root():return {"message": "Hello World"}if __name__ __main__:uvicorn.run(&quo…...

如何在 HTML 中实现响应式设计以适应不同设备的屏幕尺寸?
要在HTML中实现响应式设计以适应不同设备的屏幕尺寸,可以使用CSS媒体查询和流动布局。 以下是实现响应式设计的一些关键步骤: 使用CSS媒体查询:CSS媒体查询允许根据屏幕尺寸和设备特性应用不同的CSS样式。通过在CSS中使用media规则…...

【基础篇】第1章 Elasticsearch 引言
1.1 Elasticsearch简介 1.1.1 基本概念 Elasticsearch,一个开源的分布式搜索引擎,以其强大的搜索能力和实时数据分析能力,在大数据时代脱颖而出。它基于Apache Lucene库构建,旨在提供高效、可扩展且易于使用的全文检索解决方案。…...

在区块链技术广泛应用的情况下,C 语言如何在区块链的底层开发中发挥更有效的作用,提高性能和安全性?
C语言在区块链底层开发中发挥着重要的作用,可以提高性能和安全性。具体可以从以下几个方面进行优化: 性能优化:C语言是一种高效的编程语言,可以直接访问内存和硬件资源。在区块链底层开发中,使用C语言可以更好地利用底…...

量化投资 日周月报 2024-06-28
文章 深度学习在量化交易中的应用:在BigQuant量化交易平台的文章中,探讨了深度学习在量化交易中,特别是在因子挖掘方面的应用。文章提到,随着传统线性模型的潜力逐渐枯竭,非线性模型逐渐成为量化交易的主要探索方向。深度学习因其对非线性关系的拟合能力,在量化交易中展现…...
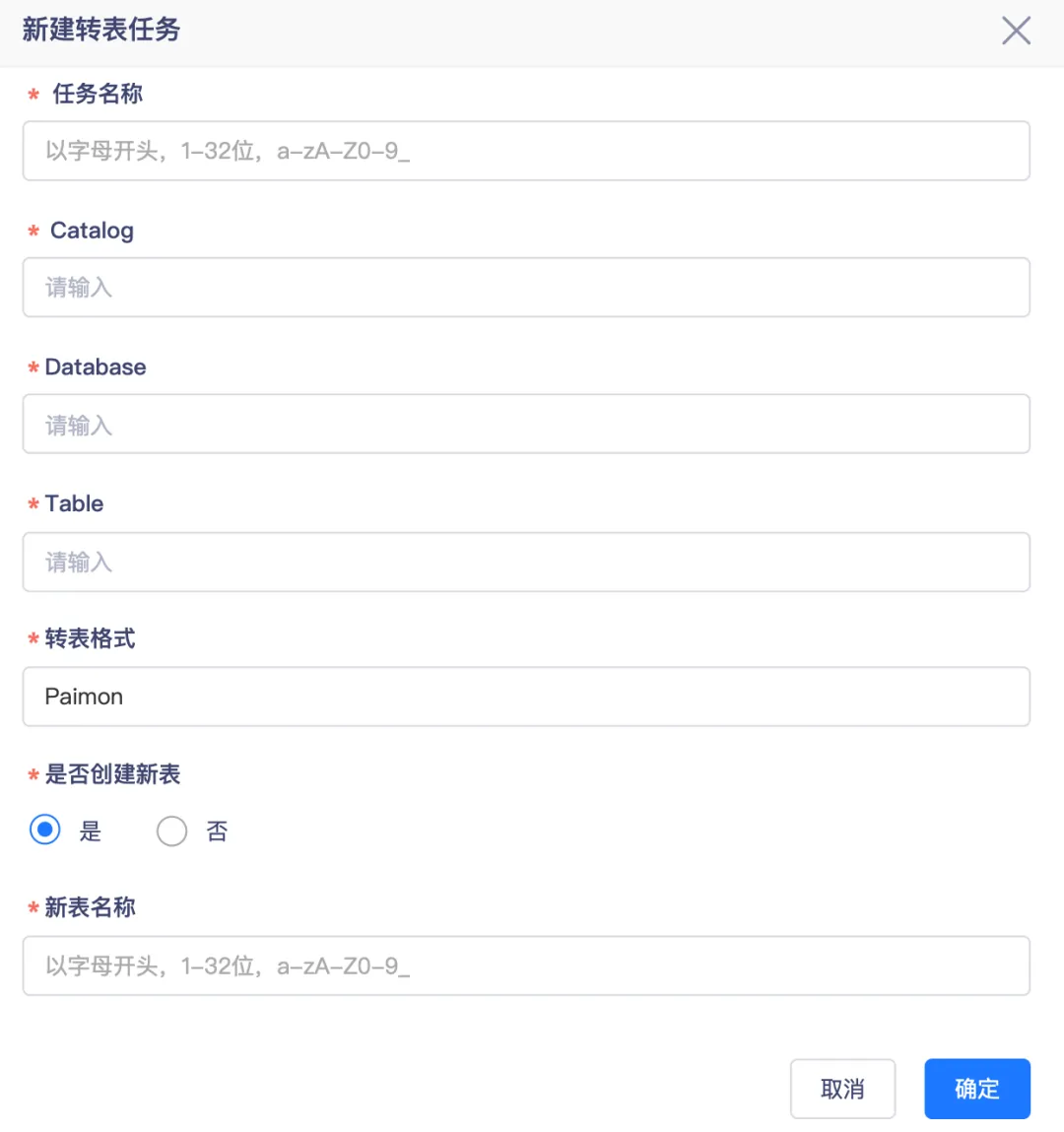
基于 Paimon 的袋鼠云实时湖仓入湖实战剖析
在当今数据驱动的时代,企业对数据的实施性能力提出了前所未有的高要求。为了应对这一挑战,构建高效、灵活且可扩展的实时湖仓成为数字化转型的关键。本文将深入探讨袋鼠云数栈如何通过三大核心实践——ChunJun 融合 Flink CDC、MySQL 一键入湖至 Paimon …...

IPython相关了解
一、什么是 IPython? 1.1 简单理解 IPython IPython 是一种增强的 Python 交互式解释器,它可以让你更方便地编写、调试和运行 Python 代码。你可以把它想象成一个比普通 Python 解释器更聪明、功能更丰富的工具,非常适合用来进行数据探索、…...
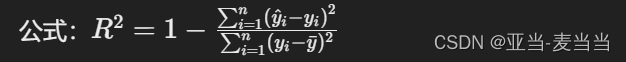
华为面试题及答案——机器学习(二)
21. 如何评价分类模型的优劣? (1)模型性能指标 准确率(Accuracy): 定义:正确分类的样本数与总样本数之比。适用:当各类样本的数量相对均衡时。精确率(Precision): 定义:预测为正类的样本中实际为正类的比例。适用:当关注假阳性错误的成本较高时(例如垃圾邮件检测…...

PlatformIO开发环境
PlatformIO是一个开源的生态系统,用于构建物联网应用,它支持多种微控制器(MCU)和硬件开发板,并且与各种IDE集成良好,如VSCode, Atom等,使得跨平台的固件开发变得更加简单和高效。 ### 平台介绍…...
 :)
In install.packages(“devtools“, verbose = TRUE) :
错误于curl::curl_download("https://r-lib.github.io/gert/libgit2-1.1.0.x86_64_legacy-linux.tar.gz", : Timeout was reached: [] Connection timed out after 10004 milliseconds 停止执行 Using PKG_CFLAGS Using PKG_LIBS-lgit2 ----------------------------…...
计算机网络 访问控制列表以及NAT
一、理论知识 1. 单臂路由 单臂路由是一种在路由器上配置多个子接口的方法,每个子接口代表不同的 VLAN,用于在一个物理接口上支持多 VLAN 通信。此方法使得不同 VLAN 之间可以通过路由器进行通信。 2. NAT (网络地址转换) NAT 是一种在私有网络和公共…...

使用Oracle IMP导入数据
使用Oracle IMP导入数据 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来聊一聊如何使用Oracle的IMP工具来导入数据。 一、什么是Oracle IMP Oracle…...

C++ 100 之 容器插入和删除
vector插入和删除操作 insert(const_iterator pos, int count,ele);//迭代器指向位置pos插入count个元素ele. push_back(ele); //尾部插入元素ele pop_back();//删除最后一个元素 erase(const_iterator start, const_iterator end);//删除迭代器从start到end之间的元素 erase(c…...

提升 Selenium 测试稳定性的秘诀:深入理解等待 API 的使用
目录 为什么需要等待Selenium 等待 API 简介隐式等待显式等待Fluent Wait等待策略的选择示例代码总结 正文 1. 为什么需要等待 在 Web 自动化测试中,等待是一个关键因素。网络应用通常是动态的,页面加载时间、元素的显示时间都可能不同步。直接操作这…...
)
Python-算法编程100例-滑动窗口(入门级)
题目1:最大连续1的个数(简单) 给定一个二进制数组 nums , 计算其中最大连续 1 的个数。 解答:前缀和双指针 # 给定一个二进制数组 nums , 计算其中最大连续 1 的个数。 from typing import Listclass So…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
