C++ 统计二进制串中0出现的个数
描述
一个32位有符号整数,使用二进制来表示,现在要统计一下二进制串中'0'的个数。
示例1
输入:
11
返回值:
29
说明:
二进制00000000000000000000000000001011中有29位0
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param n int整型 * @return int整型*/int countZeros(int n) {// write code hereint count = 0, i = 0; while(i < 32) {count += (n>>i++) & 1; //循环右移每个bit位,判断最低位是否为1,利用1&1=1, 0&1=0的性质 }return 32 - count; //统计出1的个数,用32减就得到0的个数了}
};相关文章:

C++ 统计二进制串中0出现的个数
描述 一个32位有符号整数,使用二进制来表示,现在要统计一下二进制串中0的个数。 示例1 输入: 11 返回值: 29 说明: 二进制00000000000000000000000000001011中有29位0 class Solution { public:/*** 代码中的…...

note-网络是怎样连接的6 请求到达服务器,响应返回浏览器
助记提要 服务器程序的结构套接字的指代方式MAC模块的接收过程IP模块的接收过程TCP模块处理连接包TCP模块处理数据包TCP模块的断开操作URI转换为实际文件路径URI调用程序Web服务器访问控制响应内容的类型 6章 请求到达服务器,响应返回浏览器 1 服务器概览 在数据…...
)
存储过程与函数:封装数据库逻辑的艺术(七)
引言 在上一章《事务处理》中,我们深入探讨了事务的ACID特性以及如何通过事务控制语句和隔离级别来确保数据的一致性和完整性。本章,我们将把焦点转向存储过程与函数,这是数据库系统中用于封装复杂业务逻辑和增强代码复用性的强大工具。通过…...
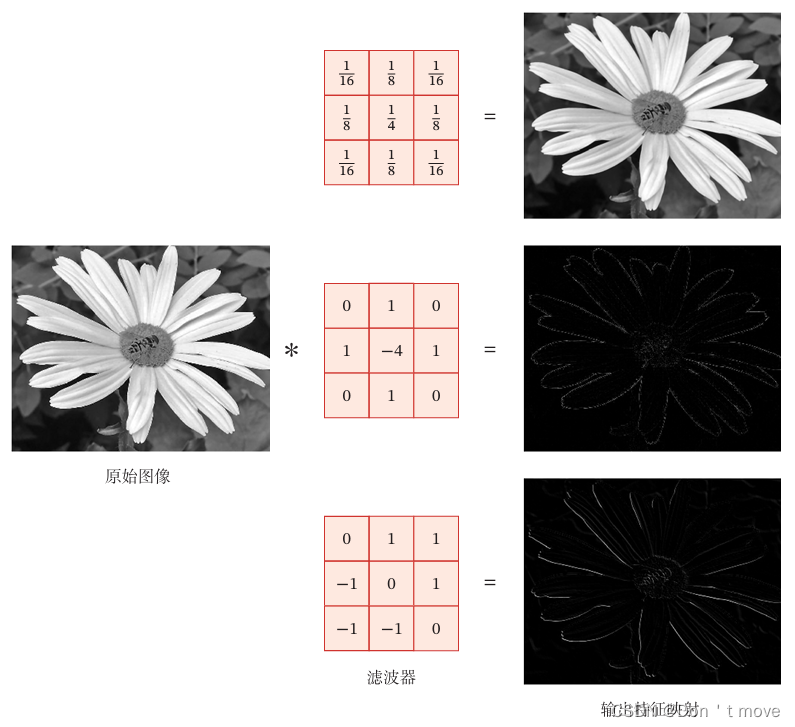
【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】卷积
卷积经常用在信号处理中,用于计算信号的延迟累积。假设一个信号发射器每个时刻 t t t产生一个信号 x t x_t xt,其信息的衰减率为 w k w_k wk,即在 k − 1 k-1 k−1个时间步长后,信息为原来的 w k w_k wk倍,时刻 …...

Trie字符串统计
Trie字符串统计 维护一个字符串集合,支持两种操作: I x 向集合中插入一个字符串 x;Q x 询问一个字符串在集合中出现了多少次。 共有 N个操作,所有输入的字符串总长度不超过 105,字符串仅包含小写英文字母。 输入格式…...

Kali Linux源
中科大 deb http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib deb-src http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib阿里云 deb http://mirrors.aliyun.com/kali kali-rolling main non-free contrib deb-src http://mirrors.…...
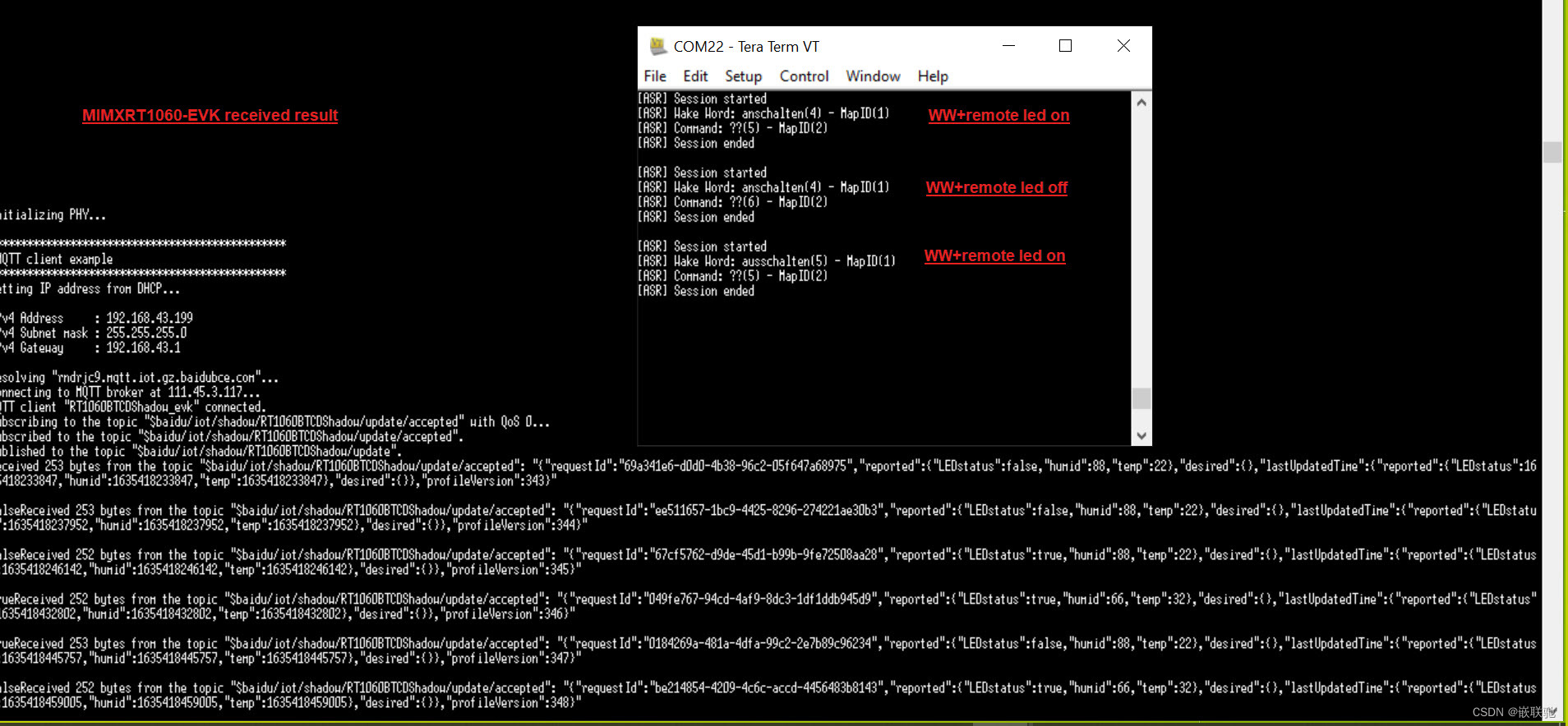
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统 一 文档简介二 平台构建2.1 使用平台2.2 百度智能云2.2.1 物联网核心套件2.2.2 在线语音合成 2.3 playback语音数据准备与烧录2.4 开机语音准备与添加2.5 唤醒词识别词命令准备与添加 三 代码准备3.1 sln-local/2-iot 代码…...
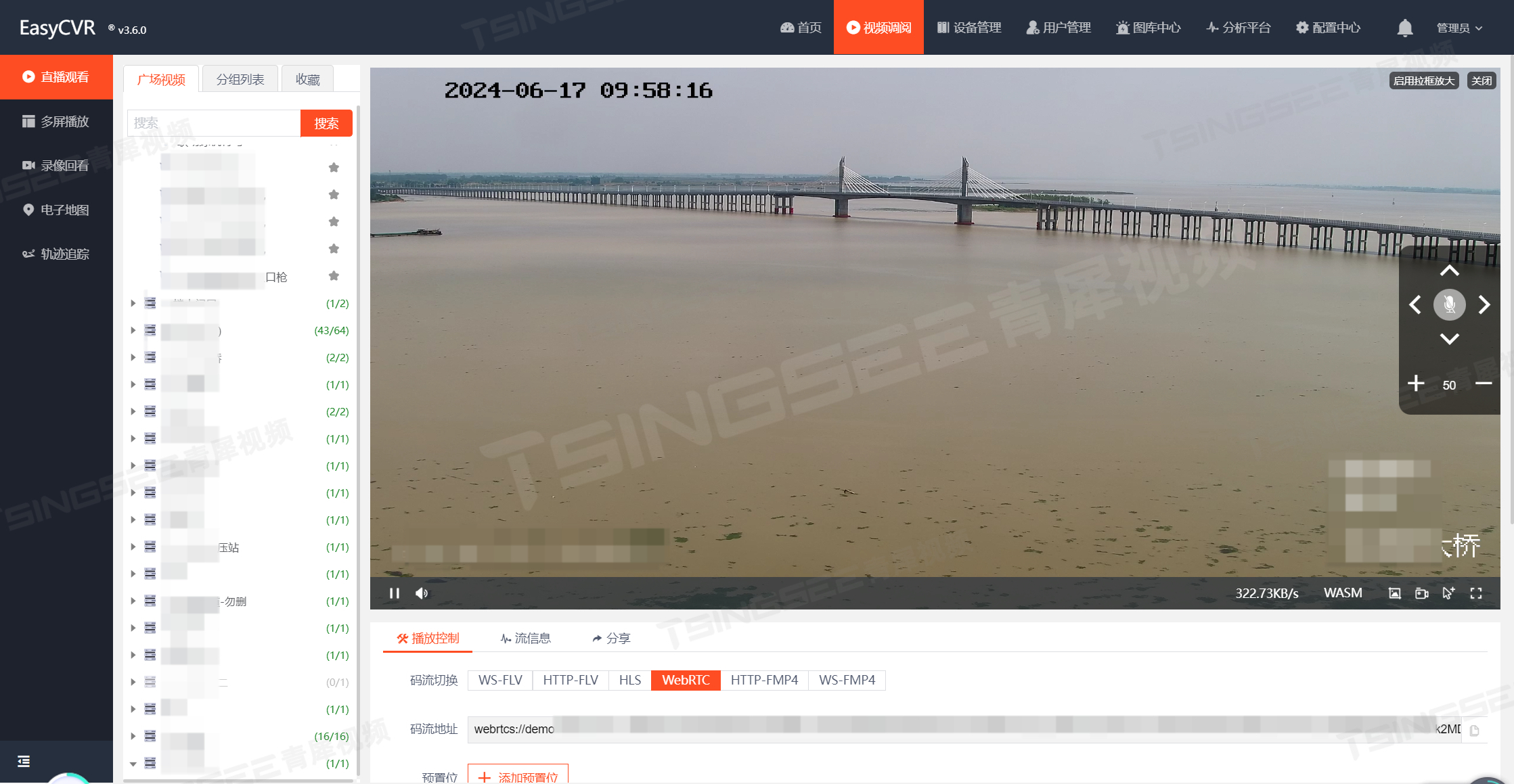
国标GB28181视频汇聚平台EasyCVR设备展示数量和显示条数不符的原因排查与解决
国标GB28181/GA/T1400协议/安防综合管理系统EasyCVR视频汇聚平台能在复杂的网络环境中,将前端设备统一集中接入与汇聚管理。智慧安防/视频存储/视频监控/视频汇聚EasyCVR平台可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级…...

FastAPI教程I
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial 第一步 import uvicorn from fastapi import FastAPIapp FastAPI()app.get("/") async def root():return {"message": "Hello World"}if __name__ __main__:uvicorn.run(&quo…...

如何在 HTML 中实现响应式设计以适应不同设备的屏幕尺寸?
要在HTML中实现响应式设计以适应不同设备的屏幕尺寸,可以使用CSS媒体查询和流动布局。 以下是实现响应式设计的一些关键步骤: 使用CSS媒体查询:CSS媒体查询允许根据屏幕尺寸和设备特性应用不同的CSS样式。通过在CSS中使用media规则…...

【基础篇】第1章 Elasticsearch 引言
1.1 Elasticsearch简介 1.1.1 基本概念 Elasticsearch,一个开源的分布式搜索引擎,以其强大的搜索能力和实时数据分析能力,在大数据时代脱颖而出。它基于Apache Lucene库构建,旨在提供高效、可扩展且易于使用的全文检索解决方案。…...

在区块链技术广泛应用的情况下,C 语言如何在区块链的底层开发中发挥更有效的作用,提高性能和安全性?
C语言在区块链底层开发中发挥着重要的作用,可以提高性能和安全性。具体可以从以下几个方面进行优化: 性能优化:C语言是一种高效的编程语言,可以直接访问内存和硬件资源。在区块链底层开发中,使用C语言可以更好地利用底…...

量化投资 日周月报 2024-06-28
文章 深度学习在量化交易中的应用:在BigQuant量化交易平台的文章中,探讨了深度学习在量化交易中,特别是在因子挖掘方面的应用。文章提到,随着传统线性模型的潜力逐渐枯竭,非线性模型逐渐成为量化交易的主要探索方向。深度学习因其对非线性关系的拟合能力,在量化交易中展现…...
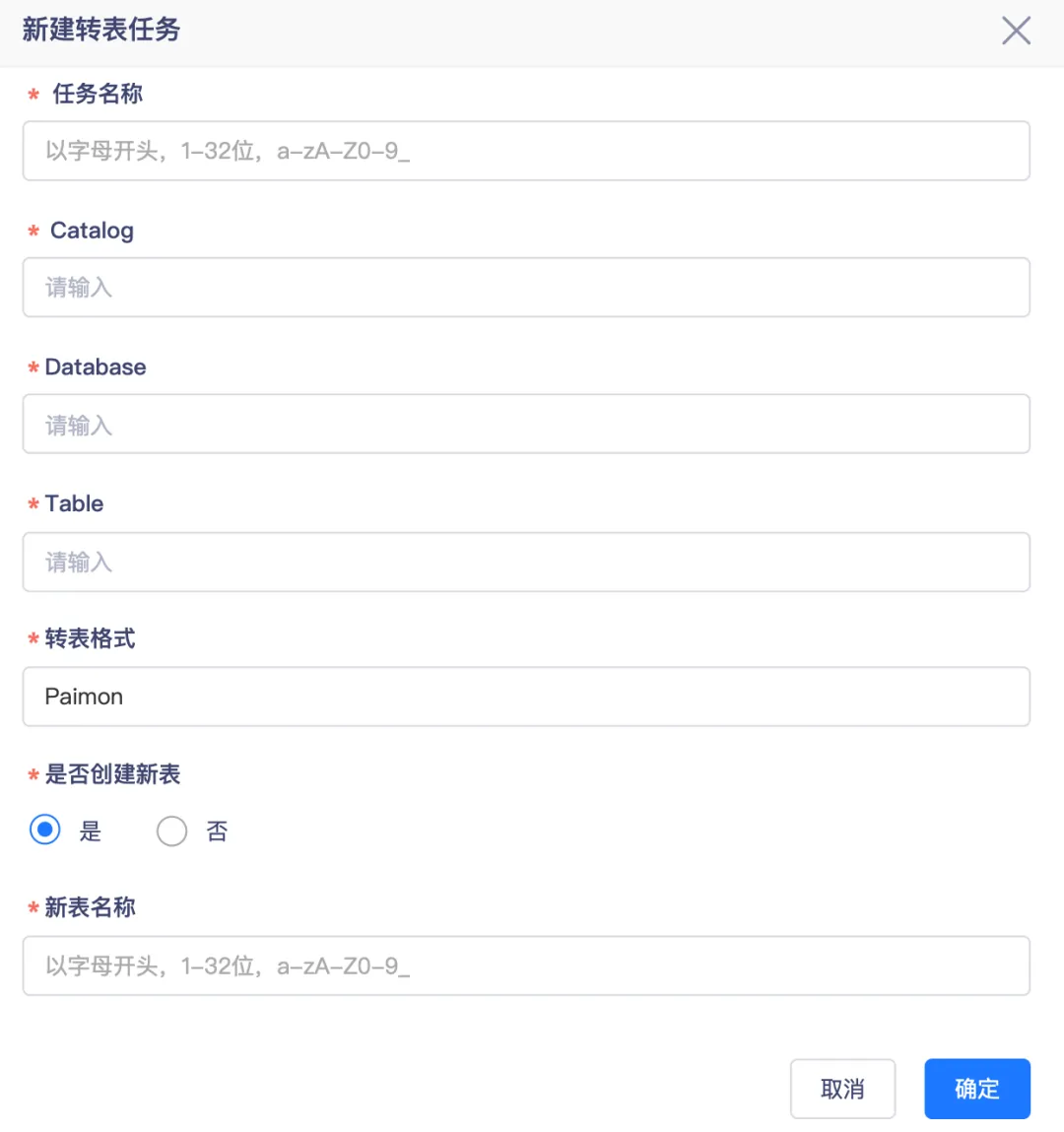
基于 Paimon 的袋鼠云实时湖仓入湖实战剖析
在当今数据驱动的时代,企业对数据的实施性能力提出了前所未有的高要求。为了应对这一挑战,构建高效、灵活且可扩展的实时湖仓成为数字化转型的关键。本文将深入探讨袋鼠云数栈如何通过三大核心实践——ChunJun 融合 Flink CDC、MySQL 一键入湖至 Paimon …...

IPython相关了解
一、什么是 IPython? 1.1 简单理解 IPython IPython 是一种增强的 Python 交互式解释器,它可以让你更方便地编写、调试和运行 Python 代码。你可以把它想象成一个比普通 Python 解释器更聪明、功能更丰富的工具,非常适合用来进行数据探索、…...
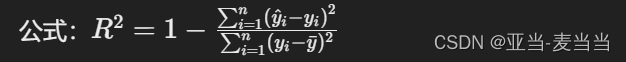
华为面试题及答案——机器学习(二)
21. 如何评价分类模型的优劣? (1)模型性能指标 准确率(Accuracy): 定义:正确分类的样本数与总样本数之比。适用:当各类样本的数量相对均衡时。精确率(Precision): 定义:预测为正类的样本中实际为正类的比例。适用:当关注假阳性错误的成本较高时(例如垃圾邮件检测…...

PlatformIO开发环境
PlatformIO是一个开源的生态系统,用于构建物联网应用,它支持多种微控制器(MCU)和硬件开发板,并且与各种IDE集成良好,如VSCode, Atom等,使得跨平台的固件开发变得更加简单和高效。 ### 平台介绍…...
 :)
In install.packages(“devtools“, verbose = TRUE) :
错误于curl::curl_download("https://r-lib.github.io/gert/libgit2-1.1.0.x86_64_legacy-linux.tar.gz", : Timeout was reached: [] Connection timed out after 10004 milliseconds 停止执行 Using PKG_CFLAGS Using PKG_LIBS-lgit2 ----------------------------…...
计算机网络 访问控制列表以及NAT
一、理论知识 1. 单臂路由 单臂路由是一种在路由器上配置多个子接口的方法,每个子接口代表不同的 VLAN,用于在一个物理接口上支持多 VLAN 通信。此方法使得不同 VLAN 之间可以通过路由器进行通信。 2. NAT (网络地址转换) NAT 是一种在私有网络和公共…...

使用Oracle IMP导入数据
使用Oracle IMP导入数据 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来聊一聊如何使用Oracle的IMP工具来导入数据。 一、什么是Oracle IMP Oracle…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
