力扣每日一题 6/28 动态规划/数组
- 博客主页:誓则盟约
- 系列专栏:IT竞赛 专栏
- 关注博主,后期持续更新系列文章
- 如果有错误感谢请大家批评指出,及时修改
- 感谢大家点赞👍收藏⭐评论✍



2742.给墙壁刷油漆【困难】
题目:
给你两个长度为 n 下标从 0 开始的整数数组 cost 和 time ,分别表示给 n 堵不同的墙刷油漆需要的开销和时间。你有两名油漆匠:
- 一位需要 付费 的油漆匠,刷第
i堵墙需要花费time[i]单位的时间,开销为cost[i]单位的钱。 - 一位 免费 的油漆匠,刷 任意 一堵墙的时间为
1单位,开销为0。但是必须在付费油漆匠 工作 时,免费油漆匠才会工作。
请你返回刷完 n 堵墙最少开销为多少。
示例 1:
输入:cost = [1,2,3,2], time = [1,2,3,2] 输出:3 解释:下标为 0 和 1 的墙由付费油漆匠来刷,需要 3 单位时间。同时,免费油漆匠刷下标为 2 和 3 的墙,需要 2 单位时间,开销为 0 。总开销为 1 + 2 = 3 。
示例 2:
输入:cost = [2,3,4,2], time = [1,1,1,1] 输出:4 解释:下标为 0 和 3 的墙由付费油漆匠来刷,需要 2 单位时间。同时,免费油漆匠刷下标为 1 和 2 的墙,需要 2 单位时间,开销为 0 。总开销为 2 + 2 = 4 。
提示:
1 <= cost.length <= 500cost.length == time.length1 <= cost[i] <= 10**61 <= time[i] <= 500
分析问题:
思路一:
首先,我们需要理解问题的本质是在给定成本和时间的列表情况下,找到满足一定体积需求的最小花费。这个问题通过定义一个 dfs 函数来解决,函数中的参数 i 表示当前考虑的物品索引,j 表示剩余需要的体积。
接下来,分析 dfs 函数的逻辑。当 j <= 0 时,表示剩余需要的体积已经满足要求,不需要再选择物品,所以返回 0 。当 i < 0 且 j > 0 时,表示没有物品可选但仍有剩余体积需求,这是不合法的情况,所以返回正无穷大 inf 。对于其他情况,有两种选择:一是选择当前物品,此时需要花费 cost[i] ,剩余需要的体积变为 j - time[i] - 1 ,然后递归调用 dfs(i - 1, j - time[i] - 1) ;二是不选择当前物品,直接递归调用 dfs(i - 1, j) 。函数返回这两种选择中的最小值。
然后,要注意到使用了 @cache 装饰器进行记忆化搜索。这是为了避免重复计算相同的子问题,提高算法的效率。
最后,在 paintWalls 方法中,通过获取 cost 列表的长度 n ,然后调用 dfs(n - 1, n) 来计算最小的花费。
思路二:
首先,定义两个匿名函数 min 和 max ,分别用于求两个数中的最小值和最大值。
然后,获取 cost 列表的长度 n ,并初始化一个列表 f 。 f[0] 设为 0 , f[1] 到 f[n] 设为正无穷大 inf 。
接下来,通过遍历 cost 和 time 列表的对应元素 c 和 t ,进行动态规划的计算。
对于每个 c 和 t ,从 n 到 1 逆序遍历 f 列表。对于每个 j ,更新 f[j] 的值。更新的方式是取当前的 f[j] 和 f[max(j - t - 1, 0)] + c 中的最小值。 max(j - t - 1, 0) 表示在考虑当前时间 t 的情况下,能够完成的工作量对应的索引。通过这种方式,我们在每个位置 j 上,都找到了使用前 j 个物品能够达到的最小花费。
最后,函数返回 f[n] ,即使用所有物品能够达到的最小花费。

代码实现:
思路一代码实现:
class Solution:def paintWalls(self, cost: List[int], time: List[int]) -> int:@cache # 记忆化搜索def dfs(i: int, j: int) -> int: # j 表示剩余需要的体积if j <= 0: # 没有约束,后面什么也不用选了return 0if i < 0: # 此时 j>0,但没有物品可选,不合法return infreturn min(dfs(i - 1, j - time[i] - 1) + cost[i], dfs(i - 1, j))n = len(cost)return dfs(n - 1, n)
思路二代码实现:
class Solution:def paintWalls(self, cost: List[int], time: List[int]) -> int:# 定义一个匿名函数min,用于求两个数的最小值min = lambda a, b: b if b < a else a# 定义一个匿名函数max,用于求两个数的最大值max = lambda a, b: b if b > a else an = len(cost)# 初始化一个列表f,f[0]为0,f[1]到f[n]为正无穷大f = [0] + [float('inf')] * n# 遍历cost和time列表的对应元素for c, t in zip(cost, time):# 从n到1逆序遍历f列表for j in range(n, 0, -1):# 更新f[j]的值,取当前f[j]和f[max(j - t - 1, 0)] + c的最小值f[j] = min(f[j], f[max(j - t - 1, 0)] + c)# 返回f[n],即完成所有工作的最小花费return f[n]
总结:
思路一代码详解:
- 定义了一个内部的
dfs函数,该函数使用了记忆化搜索(通过@cache装饰器实现)。dfs函数接受两个参数:i表示当前考虑的物品索引,j表示剩余需要的体积。 - 在
dfs函数中,如果j <= 0,表示剩余需要的体积已经满足要求,不需要再选择物品,返回0。 - 如果
i < 0且j > 0,表示没有物品可选但仍有剩余体积需求,这种情况是不合法的,返回inf(表示正无穷大)。 - 对于其他情况,有两种选择:
- 选择当前物品(索引为
i),那么需要花费cost[i],并且剩余需要的体积变为j - time[i] - 1,然后递归调用dfs(i - 1, j - time[i] - 1)。 - 不选择当前物品,直接递归调用
dfs(i - 1, j)。
- 选择当前物品(索引为
- 最后,函数返回这两种选择中的最小值。
- 在
paintWalls方法中,首先获取cost列表的长度n,然后调用dfs(n - 1, n)来计算最小的花费。
总的来说,这段代码的目的是通过递归的方式,在考虑每个物品的选择与否的情况下,计算出满足剩余体积需求的最小花费。记忆化搜索的使用可以避免重复计算,提高算法的效率。
考点:
- 动态规划:两段代码都运用了动态规划的思想来解决问题。通过定义合适的状态(如代码中的
f数组)和状态转移方程(如更新f[j]的值),来逐步求解最优解。 - 函数定义与使用:代码中定义了匿名函数(如
min和max函数)来简化比较和操作。 - 列表操作:涉及到列表的初始化、遍历(正序和逆序)以及元素的更新。
- 逻辑推理与问题分析:需要理解问题的要求,找出合适的解法,并将其转化为代码实现。
收获:
- 深入理解动态规划的概念和应用:通过实际解决这个问题,更加熟悉如何根据问题的特点定义状态和状态转移方程,从而有效地运用动态规划来求解最优解。
- 提高函数使用和定义的能力:学会了使用匿名函数来简洁地表达一些常见的操作,增强了代码的可读性和简洁性。
- 增强对列表数据结构的操作能力:包括列表的初始化、遍历和元素的修改,能够更加熟练地运用列表来解决实际问题。
- 培养逻辑思维和问题分析能力:在理解问题的基础上,能够将其转化为有效的算法和代码实现,提高了解决复杂问题的能力。
- 学会从不同的角度思考问题:两段代码虽然都解决了同一个问题,但实现方式略有不同,通过对比学习,可以拓宽解题思路,提高解决问题的灵活性。

“祈愿万家灯火熨烫过脉络,刀山与火海多深刻,都陪你渡过。”——《不痛》
相关文章:

力扣每日一题 6/28 动态规划/数组
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 2742.给墙壁刷油漆【困难】 题目: 给你两个长度为 n 下标从 0…...

[数据集][目标检测]游泳者溺水检测数据集VOC+YOLO格式8275张4类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):8275 标注数量(xml文件个数):8275 标注数量(txt文件个数):8275 标注…...
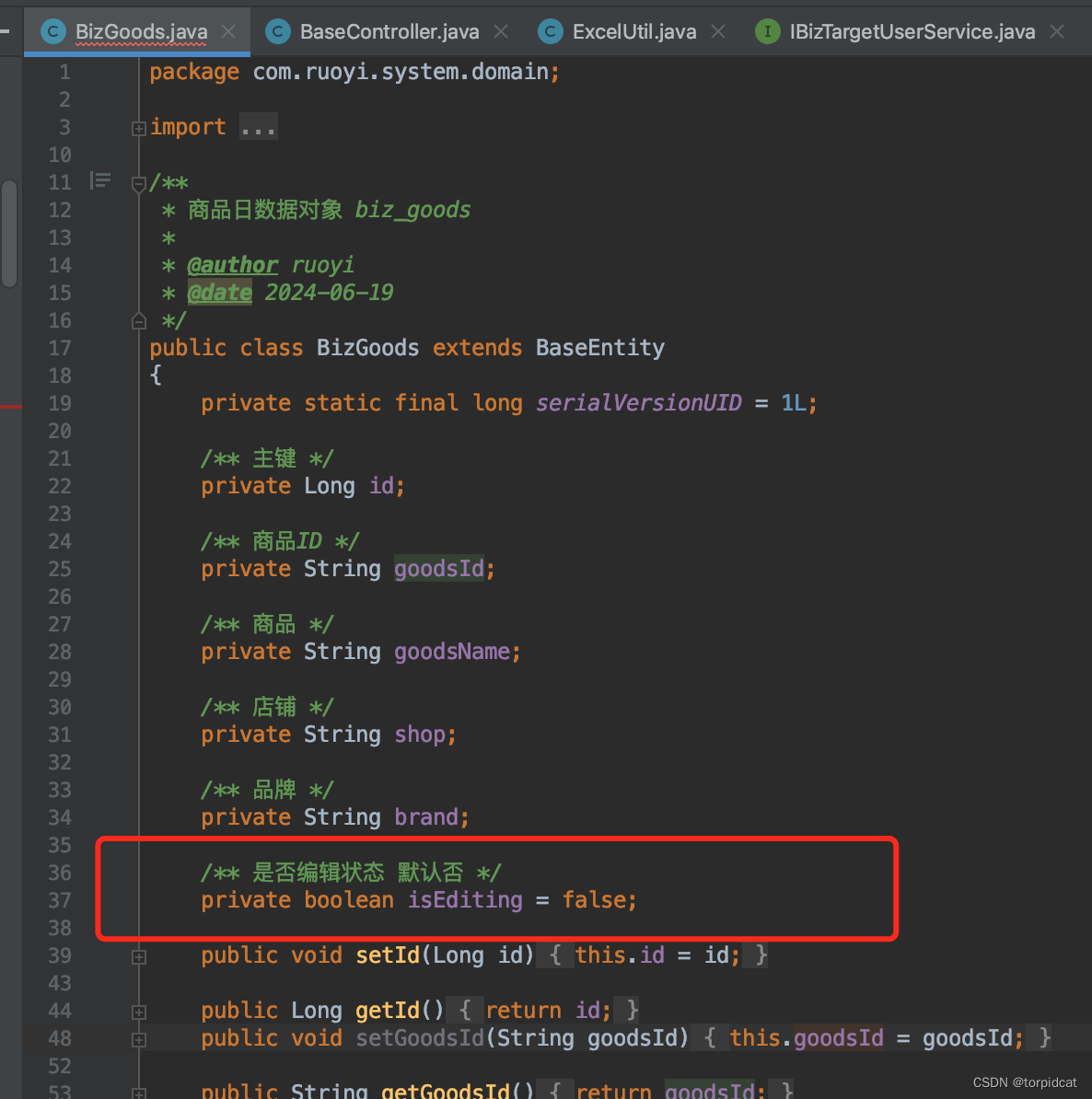
若依 ruoyi 分离版 vue 简单的行内编辑实现
需要实现的效果:双击文本 - 修改文本 - 保存修改。 原码:仅文本显示文字内容 <el-table-column label"商品" align"center" prop"goodsName" width"200" v-if"columns[1].visible" /> 实现…...

【工具】API文档生成DocFX
文章目录 总述示例第一步:安装 DocFX第二步:初始化项目第三步:编辑配置文件第四步:编写文档第五步:生成文档第六步:预览文档第七步:部署文档 总述 DocFX 是一个由微软开发的开源文档生成工具&a…...

在 JavaScript 中处理异步操作和临时事件处理程序
关键技术和设计总结 使用 Promise 和 then 进行异步操作: 我们通过使用 Promise 来处理异步操作,确保操作按顺序执行。在 getReportListByCurrentTime 函数中,返回一个 Promise 对象,保证在数据加载完成后调用 resolve,以便可以在…...
)
[Cocos Creator] v3.8开发知识点记录(持续更新)
问题:从 cc 里找不到宏定义 CC_PREVIEW 等。 解决方案:找不到就自己定义,将 declare const CC_PREVIEW; 添加到需要的ts文件里。参考:creator3d 找不到宏定义如 CC_EDITOR,CC_PREVIEW,CC_JSB - Creator 3.x…...

Excel_VBA编程
在Excel中,VBA(Visual Basic for Applications)是一种强大的工具,可以用来自动化各种任务。下面介绍一些常用的VBA函数和程序结构: 常用函数 MsgBox:用于显示消息框。 MsgBox "Hello, World!"In…...

Java中的Path类使用详解及最佳实践
Java中的Path类使用详解及最佳实践 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨Java中的Path类,这是Java标准库中用于操作文件…...

生成和查看预定义宏
参考下面的指令 arm-none-eabi-gcc -marcharmv7e-m -dM -E - < /dev/null | grep SYNC这个指令是用来生成和查看预定义宏(macros)的一种方法。让我们逐步分解和解释这个命令的各个部分: arm-none-eabi-gcc: 这是 ARM 架构下的交叉编译器…...
)
Redis 7.x 系列【12】数据类型之基数统计(HyperLogLog)
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 概述2. 常用命令2.1 PFADD2.2 PFCOUNT2.3 PFMERGE 3. 应用场景 1. 概述 基数表示数…...
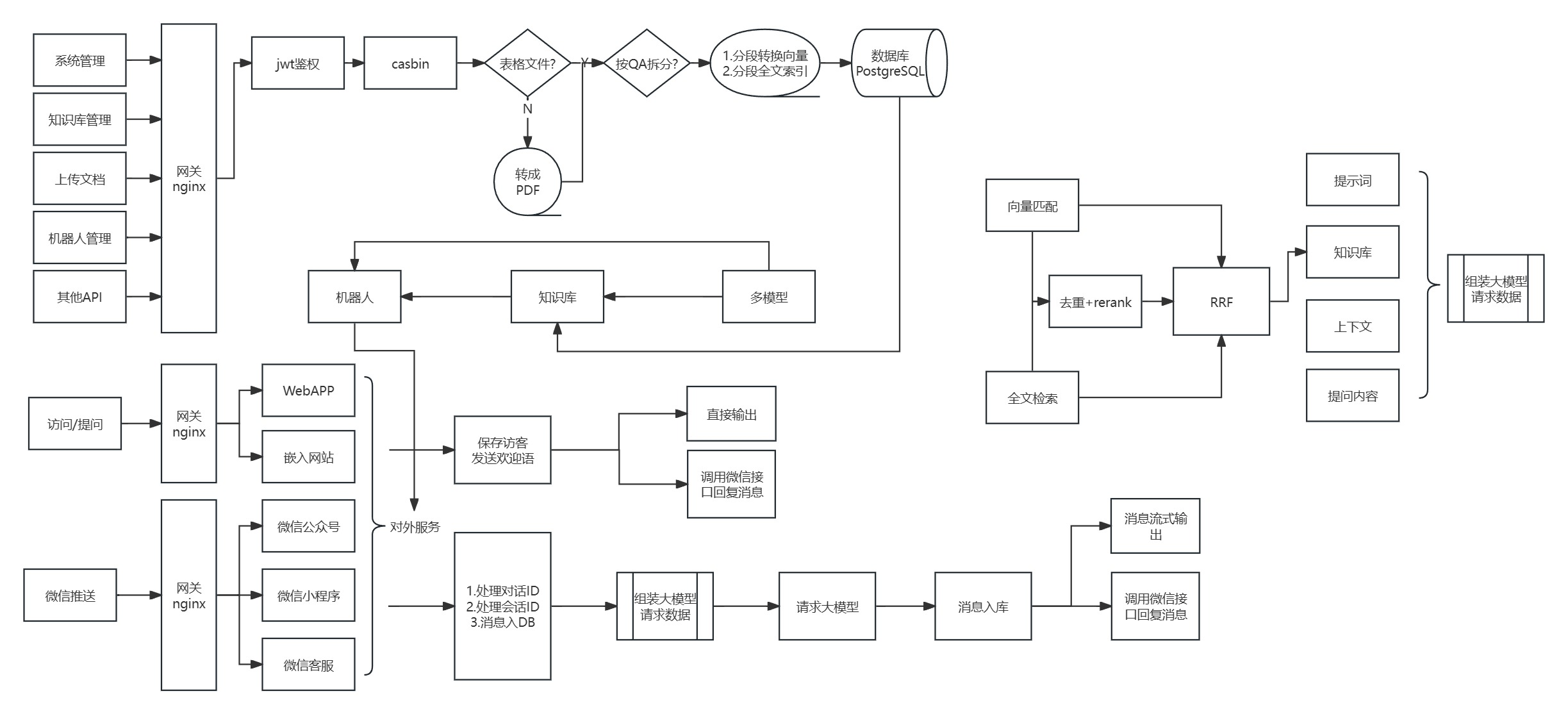
开源大模型RAG企业本地知识库问答机器人-ChatWiki
ChatWiki ChatWiki是一款开源的知识库 AI 问答系统。系统基于大语言模型(LLM )和检索增强生成(RAG)技术构建,提供开箱即用的数据处理、模型调用等能力,可以帮助企业快速搭建自己的知识库 AI 问答系统。 开…...
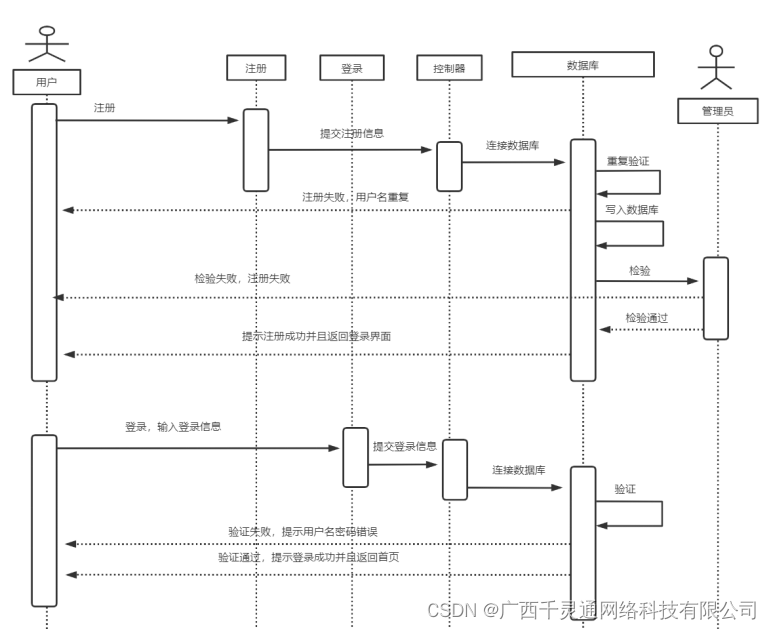
基于Java的蛋糕预定系统【附源码+LW】
摘 要 当今社会进入了科技进步、经济社会快速发展的新时代。国际信息和学术交流也不断加强,计算机技术对经济社会发展和人民生活改善的影响也日益突出,人类的生存和思考方式也产生了变化。传统购物方式采取了人工的管理方法,但这种管理方法存…...

Java框架的原理主要基于以下几个核心
本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(注明:作者:王文峰…...

已解决javax.xml.bind.MarshalException:在RMI中,参数或返回值无法被编组的正确解决方法,亲测有效!!!
已解决javax.xml.bind.MarshalException:在RMI中,参数或返回值无法被编组的正确解决方法,亲测有效!!! 目录 问题分析 出现问题的场景 服务器端代码 客户端代码 报错原因 解决思路 解决方法 1. 实现…...

仓库管理系统17--客户管理
原创不易,打字不易,截图不易,多多点赞,送人玫瑰,留有余香,财务自由明日实现 1、添加用户控件 <UserControl x:Class"West.StoreMgr.View.CustomerView"xmlns"http://schemas.microsof…...
笔记本重装系统怎么操作? windows电脑重装系统,超实用的四种方法
重新安装操作系统是维护计算机性能和确保系统稳定运行的重要步骤。对于 Windows 笔记本用户而言,熟悉重装系统的方法可以帮助他们解决各种问题,从提高系统速度到修复软件故障。然而具体来讲,笔记本重装系统怎么操作呢?接下来&…...

【高考志愿】计算机
目录 一、专业概述 二、就业方向 三、选择建议 四、注意事项 五、计算机专业学科排名 高考志愿选择计算机专业,无疑是一个充满挑战与机遇的决策。这个专业以其广泛的应用领域、前沿的技术研究和可观的就业前景,吸引了无数考生的目光。 一、专业概述…...

使用ExpandableListView创建可扩展列表
使用ExpandableListView创建可扩展列表 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨如何使用Android中的ExpandableListView创建可扩展列…...

酒店新零售模式,亚朵酒店众筹模式, 社交新零售商业模式
抓住会员的需求,通过众筹让上万铁杆粉丝成为微股东! 作为一家高端酒店,它拥有近2000万会员,这些会员还抢着掏钱帮它开酒店。而且,这家酒店还直接融资了19亿,计划上市。这家酒店在全国开设了1000多家店&…...

2010-2023年 省级、地级市、地市州盟保障性住房面积数据
保障性住房是政府为解决中低收入家庭住房问题而实施的一项重要政策,旨在通过提供限定价格或租金的住房,实现社会公平和稳定。以下是对省级、地级市、地市州盟保障性住房面积数据的介绍: 数据简介 定义:保障性住房包括廉租住房、…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
