第五十二章 BFS进阶(二)——双向广搜
第五十二章 BFS进阶(二)——双向广搜
- 一、双向广搜
- 1、优越之处
- 2、实现逻辑
- 3、复杂度分析
- 二、例题
- 1、问题
- 2、分析
- 3、代码
一、双向广搜
1、优越之处
双向广搜是指我们从终点和起点同时开始搜索,当二者到达同一个中间状态的时候,即相遇。
那么这么搜有什么好处呢?
我们知道,在很多题目中,我们使用BFS的时间复杂度是指数级别的。
也就是说,如果讲BFS的进行次数画成一个函数的话,就会画成下面这个图。
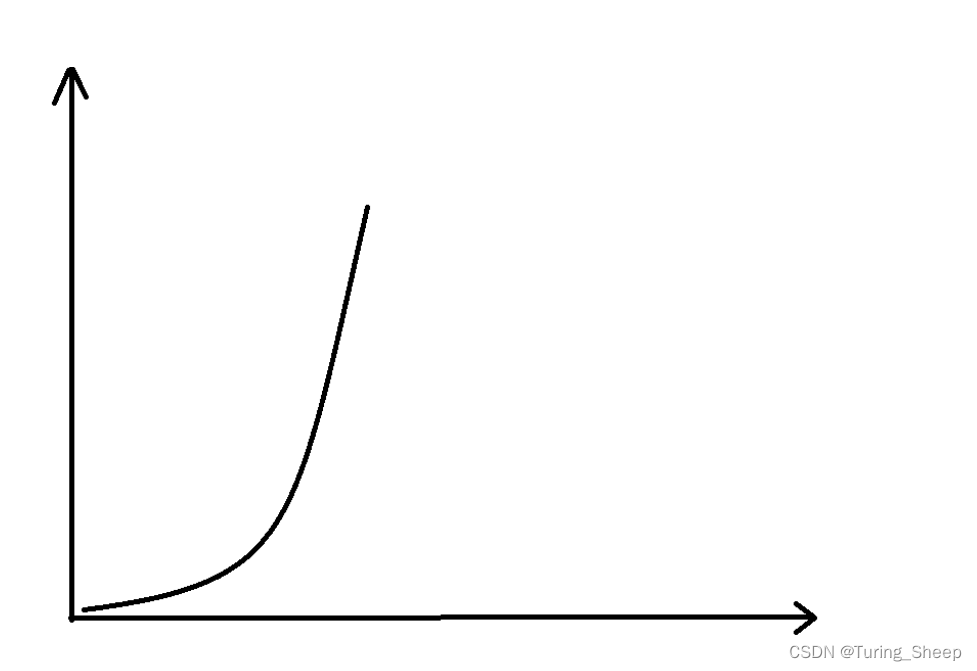
如果我们采取从两端出发,到中间某点相遇的做法。
那么示意图可以画成下面的样子:
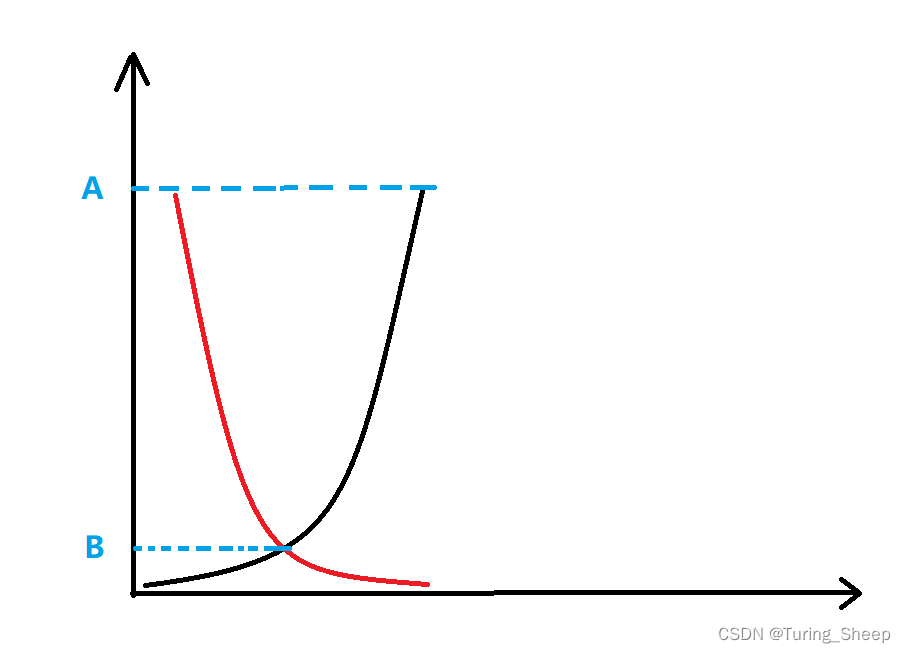
可能原来我们需要进行A次搜索,但是双向广搜的话,我们就只需要进行B次搜索。(上图仅仅表示一个大概意思,目的仅仅为了突出双向广搜进行了很大的优化,请勿追究细节)
除了上面这种大致的表示方法外,我们还可以画成一个搜索树的形式来看。
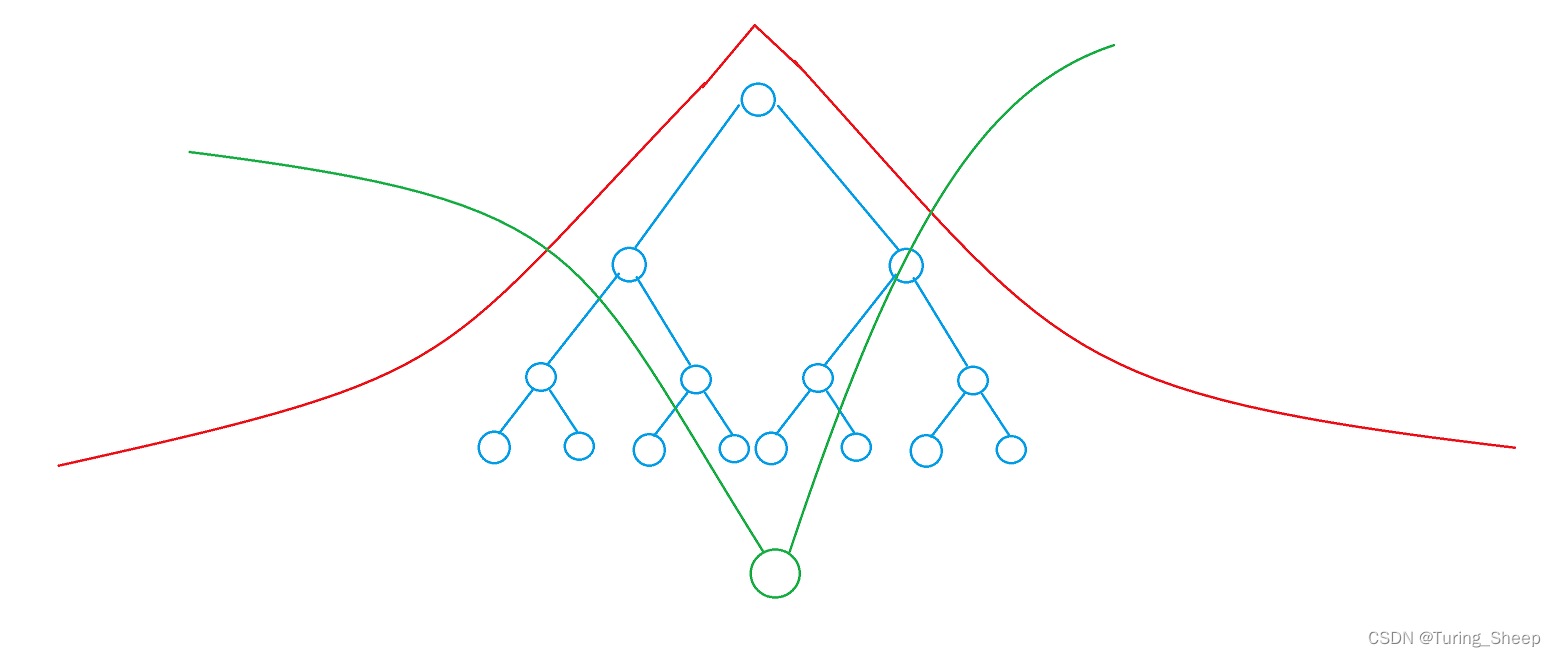
红色绿色线交叉的部分组成的菱形是双向广搜过程中所需搜索的状态数量。
上面的两个图仅仅是感性的分析了一下,双向广搜的优越之处。
我们还需要量化计算一下,到底优化了多少,具体的时间复杂度是多少,在分析复杂度之前,我们需要先看一下双向广搜大体的实现逻辑。
2、实现逻辑
我们创建两个队列。
一个队列从起点开始广搜,一个队列从终点开始广搜。
而在BFS中,我们的执行次数和队列中的元素是相关的。我们队列中的元素越多,BFS需要扩展的就越多。所以我们可以通过队列中的元素个数来代表一个BFS扩展时的复杂程度。
因此,我们可以比较两个BFS的队列中的元素,谁队列中元素少,就对哪个BFS进行拓展。
3、复杂度分析
根据上面的算法实现,我们可以知道,基本上就是从终点开始的BFS和从起点开始的BFS轮流进行。
我们可以认为二者进行的次数是一样的。
假设二者一共扩展了KKK次,那么各自可以认为进行了k/2k/2k/2次。
这里的拓展是只刚才搜索树中的层。假设每次扩展是多两个状态入队,那么总共的状态就是1+21+22....+2k/2−11 + 2^1 + 2^2 ....+2^{k/2-1}1+21+22....+2k/2−1,求和以后约等于2k/22^{k/2}2k/2,那么两个BFS加起来就是2k/2+12^{k/2+1}2k/2+1。
如果单向广搜的话,按照刚才的求和公式,对kkk层的状态求和,大概是2k2^{k}2k
那么我们就发现优化了大约2k/22^{k/2}2k/2倍。
二、例题
1、问题

2、分析
过程很简单,就是从起点开始枚举每一个可能的变化,直到最后变成了B。
由于我们已经知道了终点过程,所以可以同时从B到A开始变化。一直到二者中间状态重合。
3、代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 6;
int n;
string A, B;
string a[N], b[N];
int extend(queue<string>& q, unordered_map<string, int >&da,unordered_map<string, int>&db,string a[N], string b[N])
{int d = da[q.front()];while(q.size() && da[q.front()] == d){auto t = q.front();q.pop();for(int i = 0; i < n; i ++ ){for(int j = 0; j < t.size(); j ++ ){if(t.substr(j, a[i].size()) == a[i]){string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size());if(db.count(r))return da[t] + db[r] + 1;if(da.count(r))continue;da[r] = da[t] + 1;q.push(r);}}}}return 11;
}
int bfs()
{if(A == B)return 0;queue<string>qa, qb;unordered_map<string, int> da, db;qa.push(A), qb.push(B);da[A] = db[B] = 0;int step = 0;while(qa.size() && qb.size()){int t;if(qa.size() < qb.size()){t = extend(qa, da, db, a, b);}else{t = extend(qb, db, da, b, a);}if(t <= 10)return t;if(++step == 10)return -1;}return -1;
}void solve()
{cin >> A >> B;while(cin >> a[n] >> b[n])n ++;int t = bfs();if(t == -1)cout << "NO ANSWER!\n";else cout << t << "\n";
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
相关文章:

第五十二章 BFS进阶(二)——双向广搜
第五十二章 BFS进阶(二)——双向广搜一、双向广搜1、优越之处2、实现逻辑3、复杂度分析二、例题1、问题2、分析3、代码一、双向广搜 1、优越之处 双向广搜是指我们从终点和起点同时开始搜索,当二者到达同一个中间状态的时候,即相…...

业务建模题
一. 单选题:1.在活动图中负责在一个活动节点执行完毕后切换到另一个节点的元素是( A)。A.控制流 B.对象流 C.判断节点 D.扩展区城2.以下说法错误的是(C)。A.活动图中的开始标记一般只有一一个,而终止标记可能有多个B.判断节点的出口条件必须保证不互相重复,并且不缺…...

电子秤专用模拟数字(AD)转换器芯片HX711介绍
HX711简介HX711是一款专为高精度电子秤而设计的24 位A/D 转换器芯片。与同类型其它芯片相比,该芯片集成了包括稳压电源、片内时钟振荡器等其它同类型芯片所需要的外围电路,具有集成度高、响应速度快、抗干扰性强等优点。降低了电子秤的整机成本ÿ…...
微服务 RocketMQ-延时消息 消息过滤 管控台搜索问题
~~微服务 RocketMQ-延时消息 消息过滤 管控台搜索问题~~ RocketMQ-延时消息实现延时消息RocketMQ-消息过滤Tag标签过滤SQL标签过滤管控台搜索问题RocketMQ-延时消息 给消息设置延时时间,到一定时间,消费者才能消费的到,中间件内部通过每秒钟扫…...
)
js发送邮件(node.js)
以前看别人博客留言或者评论文章时必须填写邮箱信息,感觉甚是麻烦。 后来才知道是为了在博主回复后让访客收到邮件,用心良苦。 于是我也在新增留言和文章评论的接口里,新增了给自己发送邮件提醒的功能。 我用的QQ邮箱,具体如下…...

English Learning - Day58 一周高频问题汇总 2023.2.12 周日
English Learning - Day58 一周高频问题汇总 2023.2.12 周日这周主要内容继续说说状语从句结果状语从句这周主要内容 DAY58【周日总结】 一周高频问题汇总 (打卡作业详见 Day59) 一近期主要讲了 一 01.主动脉修饰 以下是最常问到的知识点拓展ÿ…...
【微电网】基于风光储能和需求响应的微电网日前经济调度(Python代码实现)
目录 1 概述 2 知识点及数学模型 3 算例实现 3.1算例介绍 3.2风光参与的模型求解 3.3 风光和储能参与的模型求解 3.5 风光储能和需求响应都参与模型求解 3.6 结果分析对比 4 Python代码及算例数据 1 概述 近年来,微电网、清洁能源等已成为全球关注的热点…...

四种方式的MySQL安装
mysql安装常见的方法有四种序号 安装方式 说明1 yum\rpm简单、快速,不能定制参数2二进制 解压,简单配置就可使用 免安装 mysql-a.b.c-linux2.x-x86_64.tar.gz3源码编译 可以定制参数,安装时间长 mysql-a.b.c.tar.gz4源码制成rpm包 把源码制…...

软考高级信息系统项目管理师系列之九:项目范围管理
软考高级信息系统项目管理师系列之九:项目范围管理 一、范围管理输入、输出、工具和技术表二、范围管理概述三、规划范围管理四、收集需求1.收集需求:2.需求分类3.收集需求的工具与技术4.收集需求过程主要输出5.需求文件内容6.需求管理7.可跟踪性8.双向可跟踪性9.需求跟踪矩阵…...

【项目精选】javaEE健康管理系统(论文+开题报告+答辩PPT+源代码+数据库+讲解视频)
点击下载源码 javaEE健康管理系统主要功能包括:教师登录退出、教师饮食管理、教师健康日志、体检管理等等。本系统结构如下: (1)用户模块: 实现登录功能 实现用户登录的退出 实现用户注册 (2)教…...

ctfshow nodejs
web 334 大小写转换特殊字符绕过。 “ı”.toUpperCase() ‘I’,“ſ”.toUpperCase() ‘S’。 “K”.toLowerCase() ‘k’. payload: CTFſHOW 123456web 335 通过源码可知 eval(xxx),eval 中可以执行 js 代码,那么我们可以依此执行系…...

无线传感器原理及方法|重点理论知识|2021年19级|期末考试
Min-Max定位 【P63】 最小最大法的基本思想是依据未知节点到各锚节点的距离测量值及锚节点的坐标构造若干个边界框,即以参考节点为圆心,未知节点到该锚节点的距离测量值为半径所构成圆的外接矩形,计算外接矩形的质心为未知节点的估计坐标。 多边定位法的浮点运算量大,计算代…...

带你写出符合 Promise/A+ 规范 Promise 的源码
Promise是前端面试中的高频问题,如果你能根据PromiseA的规范,写出符合规范的源码,那么我想,对于面试中的Promise相关的问题,都能够给出比较完美的答案。 我的建议是,对照规范多写几次实现,也许…...

回流与重绘
触发回流与重绘条件👉回流当渲染树中部分或者全部元素的尺寸、结构或者属性发生变化时,浏览器会重新渲染部分或者全部文档的过程就称为 回流。引起回流原因1.页面的首次渲染2.浏览器的窗口大小发生变化3.元素的内容发生变化4.元素的尺寸或者位置发生变化…...
openpyxl表格的简单实用
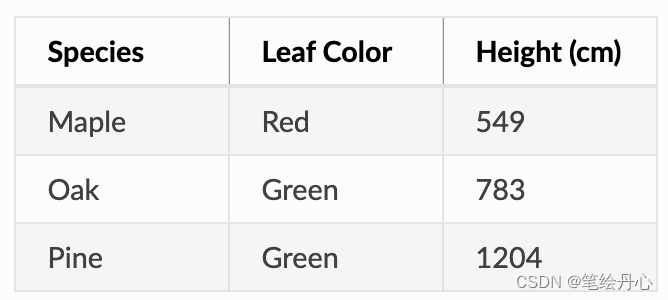
示例:创建简单的电子表格和条形图 在这个例子中,我们将从头开始创建一个工作表并添加一些数据,然后绘制它。我们还将探索一些有限的单元格样式和格式。 我们将在工作表上输入的数据如下: 首先,让我们加载 openpyxl 并创建一个新工作簿。并获取活动表。我们还将输入我们…...

【寒假day4】leetcode刷题
🌈一、选择题❤1.下列哪一个是析构函数的特征( )。A: 析构函数定义只能在类体内 B: 一个类中只能定义一个析构函数 C: 析构函数名与类名相同 D: 析构函数可以有一个或多个参数答案:B答案解析:析构函数是构造函…...

【竞赛题】6355. 统计公平数对的数目
题目: 给你一个下标从 0 开始、长度为 n 的整数数组 nums ,和两个整数 lower 和 upper ,返回 公平数对的数目 。 如果 (i, j) 数对满足以下情况,则认为它是一个 公平数对 : 0 < i < j < n,且 l…...
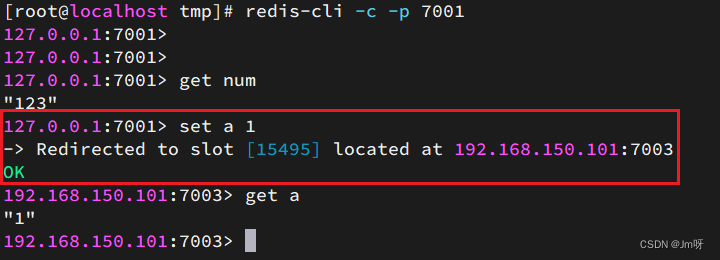
Redis集群搭建(主从、哨兵、分片)
1.单机安装Redis 首先需要安装Redis所需要的依赖: yum install -y gcc tcl然后将课前资料提供的Redis安装包上传到虚拟机的任意目录: 例如,我放到了/tmp目录: 解压缩: tar -xzf redis-6.2.4.tar.gz解压后࿱…...

Dart语法基础补充
Asynchrony support Dart 库中充满了返回 Future 或 Stream 对象的函数。 这些函数是异步的:它们在设置一个可能耗时的操作(例如 I/O)后返回,而不等待该操作完成。 async 和 await 关键字支持异步编程,让编写看起来类…...

Nginx - 深入理解nginx的处理请求、进程关系和配置文件重载
概述 Nginx的系统学习整理的第三篇博客,主要介绍nginx的应用场景和架构基础,以便更好的理解,再生产环境中进行性能调优。 Nginx的三个主要应用场景 1.静态资源服务,通过本地文件系统提供服务 2.反向代理服务,强大的性…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Modbus转Ethernet IP深度解析:磨粉设备效率跃升的底层技术密码
在建材矿粉磨系统中,开疆智能Modbus转Ethernet IP网关KJ-EIP-101的应用案例是一个重要的技术革新。这个转换过程涉及到两种主要的通信协议:Modbus和Ethernet IP。Modbus是一种串行通信协议,广泛应用于工业控制系统中。它简单、易于部署和维护…...

LeetCode 2894.分类求和并作差
目录 题目: 题目描述: 题目链接: 思路: 思路一详解(遍历 判断): 思路二详解(数学规律/公式): 代码: Java思路一(遍历 判断&a…...

CSS(2)
文章目录 Emmet语法快速生成HTML结构语法 Snipaste快速生成CSS样式语法快速格式化代码 快捷键(VScode)CSS 的复合选择器什么是复合选择器交集选择器后代选择器(重要)子选择器(重要)并集选择器(重要)**链接伪类选择器**focus伪类选…...
