逻辑回归梯度推导
逻辑回归是一种广泛使用的分类算法,用于估计一个事件发生的概率。它是线性回归的扩展,通过sigmoid函数将线性回归的输出映射到[0, 1]区间,从而用于分类任务。
在逻辑回归中,我们使用对数似然损失函数(log-likelihood loss function)来衡量模型预测值与真实值之间的差异。我们的目标是最小化这个损失函数,以找到最优的模型参数。
假设我们有以下符号:
- h θ ( x ) h_{\theta}(x) hθ(x) 是模型预测的概率, h θ ( x ) = 1 1 + e − θ T x h_{\theta}(x) = \frac{1}{1 + e^{-\theta^T x}} hθ(x)=1+e−θTx1。
- m m m 是训练样本的数量。
- y y y 是实际输出标签,取值为0或1。
- θ \theta θ 是模型参数。
- x x x 是单个训练样本的特征向量。
对数似然损失函数为(也可以说是交叉熵损失,来源于KL散度的后一项):
L ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] L(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_{\theta}(x^{(i)}))] L(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
为了找到最小化损失函数的参数 θ \theta θ,我们需要计算损失函数关 $\theta $ 的梯度。以下是梯度计算的过程:
对 $ L(\theta) $ 求关于$ \theta_j $ 的偏导数:
∂ ∂ θ j L ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) ∂ ∂ θ j log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) ∂ ∂ θ j log ( 1 − h θ ( x ( i ) ) ) ] = − 1 m ∑ i = 1 m [ y ( i ) h θ ( x ( i ) ) ∂ ∂ θ j h θ ( x ( i ) ) − 1 − y ( i ) 1 − h θ ( x ( i ) ) ∂ ∂ θ j h θ ( x ( i ) ) ] = − 1 m ∑ i = 1 m [ y ( i ) 1 h θ ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ] ∂ ∂ θ j h θ ( x ( i ) ) \begin{align*} \frac{\partial}{\partial \theta_j} L(\theta) &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \frac{\partial}{\partial \theta_j} \log(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) \frac{\partial}{\partial \theta_j} \log(1 - h_{\theta}(x^{(i)})) \right] \\ &= -\frac{1}{m} \sum_{i=1}^{m} \left[ \frac{y^{(i)}}{h_{\theta}(x^{(i)})} \frac{\partial}{\partial \theta_j} h_{\theta}(x^{(i)}) - \frac{1 - y^{(i)}}{1 - h_{\theta}(x^{(i)})} \frac{\partial}{\partial \theta_j} h_{\theta}(x^{(i)}) \right] \\ &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \frac{1}{h_{\theta}(x^{(i)})} - (1 - y^{(i)}) \frac{1}{1 - h_{\theta}(x^{(i)})} \right] \frac{\partial}{\partial \theta_j} h_{\theta}(x^{(i)}) \end{align*} ∂θj∂L(θ)=−m1i=1∑m[y(i)∂θj∂log(hθ(x(i)))+(1−y(i))∂θj∂log(1−hθ(x(i)))]=−m1i=1∑m[hθ(x(i))y(i)∂θj∂hθ(x(i))−1−hθ(x(i))1−y(i)∂θj∂hθ(x(i))]=−m1i=1∑m[y(i)hθ(x(i))1−(1−y(i))1−hθ(x(i))1]∂θj∂hθ(x(i))
计算 h θ ( x ) h_{\theta}(x) hθ(x) 关于 θ j \theta _{j} θj的偏导数:
∂ ∂ θ j h θ ( x ) = ∂ ∂ θ j ( 1 1 + e − θ T x ) = e − θ T x ( 1 + e − θ T x ) 2 ∂ ∂ θ j ( − θ T x ) = e − θ T x ( 1 + e − θ T x ) 2 ( − x j ) = h θ ( x ) ( 1 − h θ ( x ) ) ( − x j ) \begin{align*} \frac{\partial}{\partial \theta_j} h_{\theta}(x) &= \frac{\partial}{\partial \theta_j} \left( \frac{1}{1 + e^{-\theta^T x}} \right) \\ &= \frac{e^{-\theta^T x}}{(1 + e^{-\theta^T x})^2} \frac{\partial}{\partial \theta_j} (-\theta^T x) \\ &= \frac{e^{-\theta^T x}}{(1 + e^{-\theta^T x})^2} (-x_j) \\ &= h_{\theta}(x) (1 - h_{\theta}(x)) (-x_j) \\ \end{align*} ∂θj∂hθ(x)=∂θj∂(1+e−θTx1)=(1+e−θTx)2e−θTx∂θj∂(−θTx)=(1+e−θTx)2e−θTx(−xj)=hθ(x)(1−hθ(x))(−xj)
将 ( ∂ ∂ θ j h θ ( x ) \frac{\partial}{\partial \theta_j} h_{\theta}(x) ∂θj∂hθ(x) ) 的结果代入梯度公式中:
∂ ∂ θ j L ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) 1 h θ ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ] h θ ( x ) ( 1 − h θ ( x ) ) ( − x j ) = − 1 m ∑ i = 1 m [ y ( i ) ( 1 − h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) h θ ( x ( i ) ) ] ( − x j ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) − h θ ( x ( i ) ) ] ( − x j ( i ) ) \begin{align*} \frac{\partial}{\partial \theta_j} L(\theta) &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \frac{1}{h_{\theta}(x^{(i)})} - (1 - y^{(i)}) \frac{1}{1 - h_{\theta}(x^{(i)})} \right]h_{\theta}(x) (1 - h_{\theta}(x)) (-x_j) \\ &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} (1 - h_{\theta}(x^{(i)})) - (1 - y^{(i)}) h_{\theta}(x^{(i)}) \right] (-x_j^{(i)}) \\ &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} - h_{\theta}(x^{(i)}) \right] (-x_j^{(i)}) \end{align*} ∂θj∂L(θ)=−m1i=1∑m[y(i)hθ(x(i))1−(1−y(i))1−hθ(x(i))1]hθ(x)(1−hθ(x))(−xj)=−m1i=1∑m[y(i)(1−hθ(x(i)))−(1−y(i))hθ(x(i))](−xj(i))=−m1i=1∑m[y(i)−hθ(x(i))](−xj(i))
因此,逻辑回归损失函数 L ( θ ) L(\theta) L(θ) 关于参数 θ j \theta_j θj的梯度是:
∂ ∂ θ j L ( θ ) = − 1 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] x j ( i ) \frac{\partial}{\partial \theta_j} L(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ h_{\theta}(x^{(i)}) - y^{(i)} \right] x_j^{(i)} ∂θj∂L(θ)=−m1i=1∑m[hθ(x(i))−y(i)]xj(i)
这个梯度表达式告诉我们,对于每个参数 θ j \theta_j θj,我们需要计算模型预测 h θ ( x ( i ) ) h_{\theta}(x^{(i)}) hθ(x(i)) 和实际标签 y ( i ) y^{(i)} y(i) 之间的差异,然后将这个差异乘以特征 x j ( i ) x_j^{(i)} xj(i),最后对所有训练样本求和并除以样本数量 m m m。这个梯度用于在优化过程中更新参数 θ j \theta_j θj,以最小化损失函数。
相关文章:

逻辑回归梯度推导
逻辑回归是一种广泛使用的分类算法,用于估计一个事件发生的概率。它是线性回归的扩展,通过sigmoid函数将线性回归的输出映射到[0, 1]区间,从而用于分类任务。 在逻辑回归中,我们使用对数似然损失函数(log-likelihood l…...

Python 使用函数输出一个整数的逆序数
在Python中,你可以定义一个函数来输出一个整数的逆序数。这里有一个简单的实现方法: def reverse_integer(x):# 检查输入是否为整数if not isinstance(x, int):raise ValueError("Input must be an integer")# 将整数转换为字符串,…...
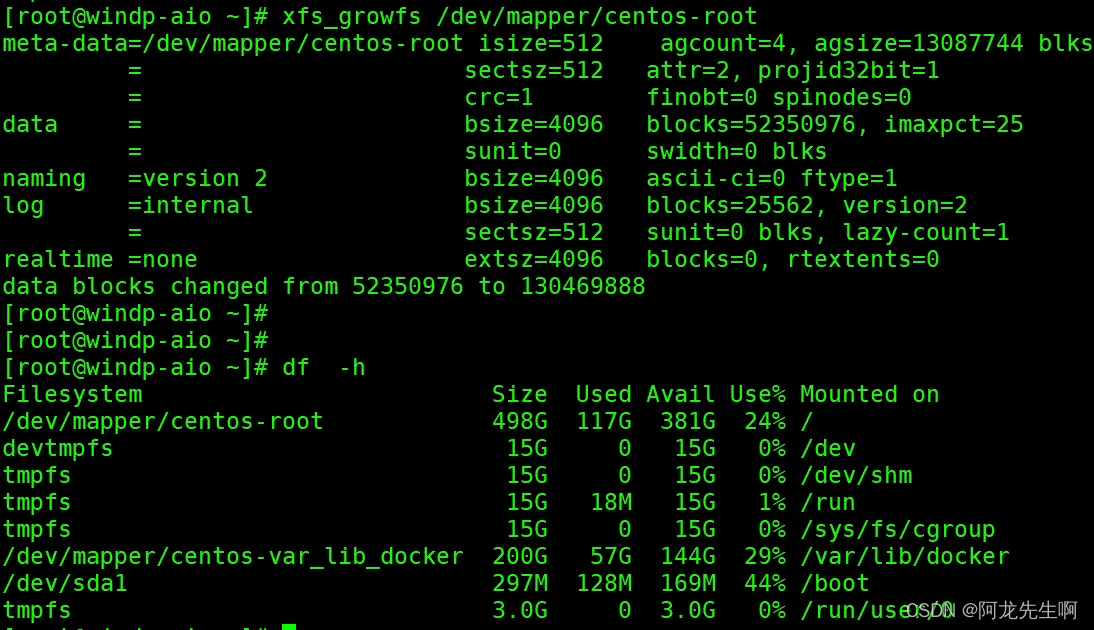
【Linux】Wmware Esxi磁盘扩容
目录 一、概述 1.1 磁盘分区概念 1.2 LVM概念 二、扩容步骤 二、报错 一、概述 1.1 磁盘分区概念 在 Linux 中,每一个硬件设备都映射到一个系统的文件,对于硬盘、光驱等 IDE 或 SCSI 设备也不例外。Linux把各种 IDE 设备分配了一个由 hd 前缀组成的文…...
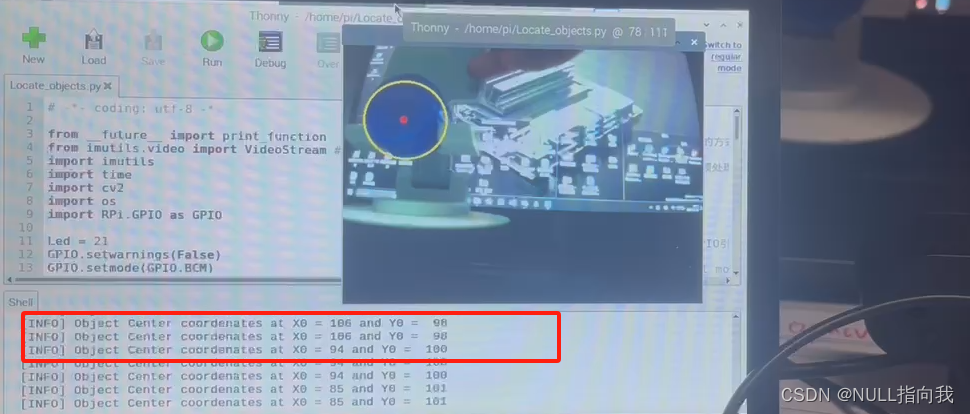
树莓派4B_OpenCv学习笔记15:OpenCv定位物体实时坐标
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: 今日学习 OpenCv定位物体实时位置,代码来源是…...

MySQL之如何定位慢查询
1、如何定位慢查询 1.1、使用开源工具 调试工具:Arthas 运维工具:Promethuss、Skywalking 1.2、MySQL自带慢日志 慢查询日志记录了所有执行时间超过指定参数(long_query_time,单位:秒,默认10秒&#x…...

Open3D 删除点云中重复的点
目录 一、算法原理1、重叠点2、主要函数二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、重叠点 原始点云克隆一份 构造重叠区域 合并点云获得重叠点 2、主要…...

填报志愿选专业是兴趣重要还是前景重要?
进行专业评估,找到一个适合自己的专业是一件非常困难的事情。在进行专业选择时,身上理想化色彩非常严重的人,会全然不顾及他人的劝阻,义无反顾的以兴趣为主,选择自己热爱的专业。一些较多考虑他人建议,能听…...

python开发基础——day9 函数基础与函数参数
一、初识函数(function) 编程函数!数学函数,里面的是逻辑,功能,而不是套公式 编程函数的作用实现特定操作的一段代码 你现在请客,每个人都点同样的一份吃的,请100个人 1.薯条 2.上校鸡块 3.可乐 那…...
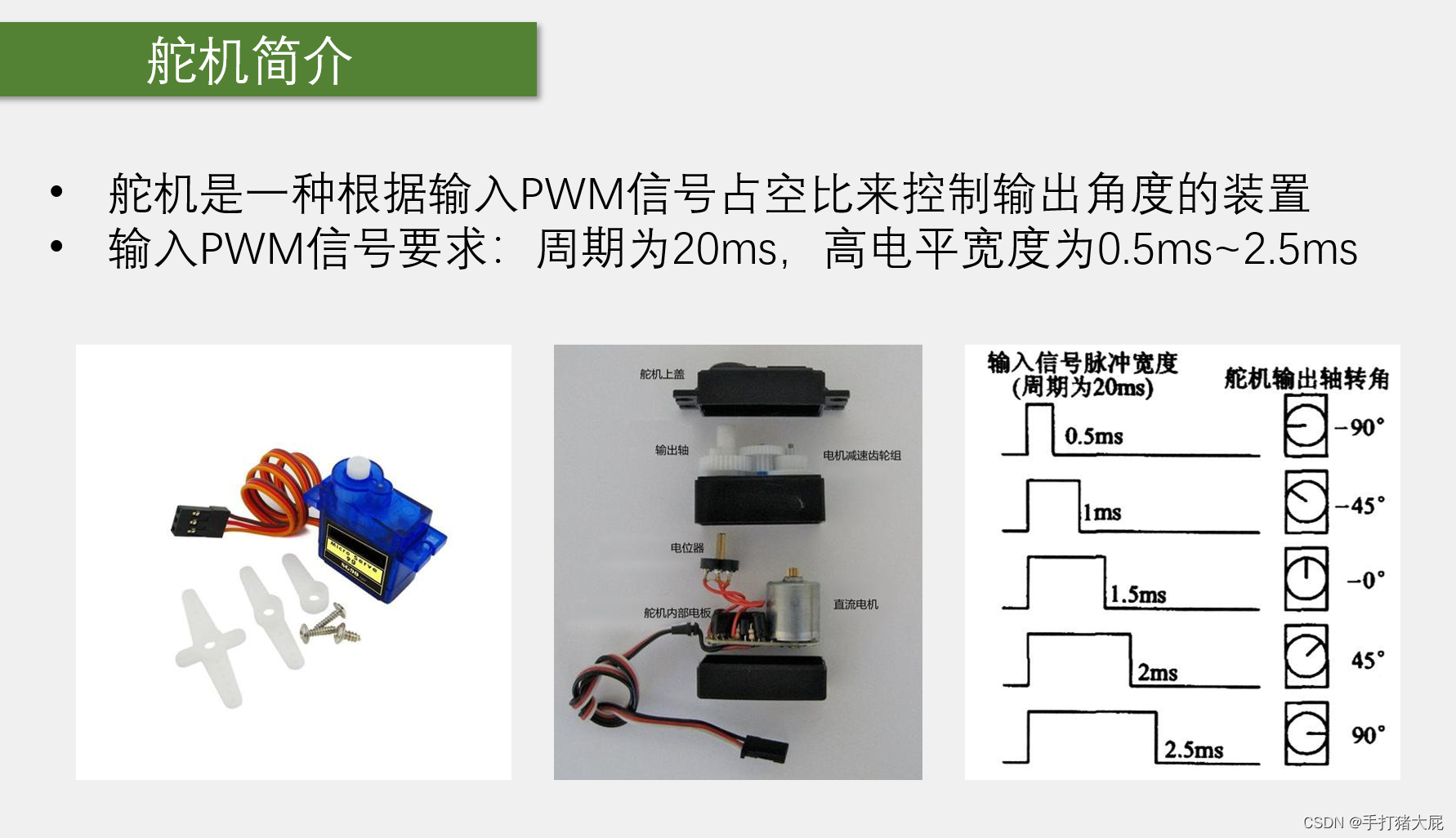
STM32——使用TIM输出比较产生PWM波形控制舵机转角
一、输出比较简介: 只有高级定时器和通用寄存器才有输入捕获/输出比较电路,他们有四个CCR(捕获/比较寄存器),共用一个CNT(计数器),而输出比较功能是用来输出PWM波形的。 红圈部分…...
(Python))
第十五章 集合(set)(Python)
文章目录 前言一、集合 前言 集合(set)是一个无序的不重复元素序列。 一、集合 set {1, 2, 3, 4}...

面试-javaIO机制
1.BIO BIO:是传统的javaIO以及部分java.net下部分接口和类。例如,socket,http等,因为网络通信同样是IO行为。传统IO基于字节流和字符流进行操作。提供了我们最熟悉的IO功能,譬如基于字节流的InputStream 和OutputStream.基于字符流…...

在.NET Core中,config和ConfigureServices的区别和作用
在.NET Core中,config和ConfigureServices是两个不同的概念,它们在应用程序的启动和配置过程中扮演着不同的角色。 ConfigureServices:这是ASP.NET Core应用程序中的一个方法,位于Startup类的内部。它的作用是配置依赖注入(DI)容器…...

App Inventor 2 如何实现多个定时功能?
1、可以使用多个“计时器”组件。 2、也可以用一个计时器,定时一分钟。也就是一分钟就会触发一次事件执行,定义一个全局数字变量,在事件中递增,用逻辑判断这个变量的值即可完成多个想要定时的任务(о∀о) 代码块请参考…...

技术驱动的音乐变革:AI带来的产业重塑
📑引言 近一个月来,随着几款音乐大模型的轮番上线,AI在音乐产业的角色迅速扩大。这些模型不仅将音乐创作的门槛降至前所未有的低点,还引发了一场关于AI是否会彻底颠覆音乐行业的激烈讨论。从初期的兴奋到现在的理性审视࿰…...
重生之我要学后端0--HTTP协议和RESTful APIs
http和RESTful APIs HTTP协议RESTful APIs设计RESTful API设计实例 HTTP协议 HTTP(超文本传输协议)是用于分布式、协作式和超媒体信息系统的应用层协议。它是网页数据通讯的基础。工作原理简述如下: 客户端请求(Request…...
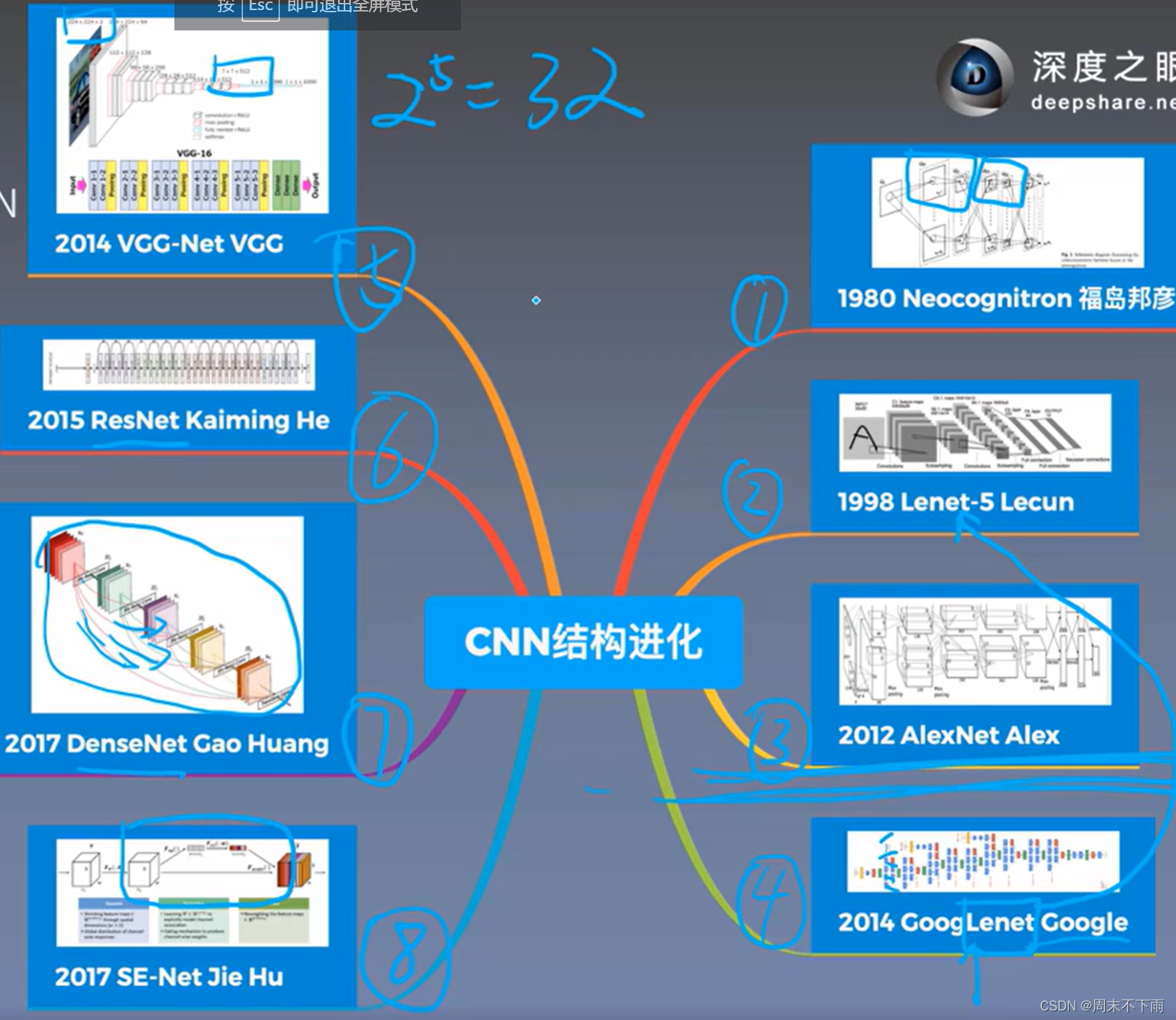
深度之眼(二十八)——神经网络基础知识(三)-卷积神经网络
文章目录 一、前言二、卷积操作2.1 填充(padding)2.2 步长2.3 输出特征图尺寸计算2.4 多通道卷积 三、池化操作四、Lenet-5及CNN结构进化史4.1 Lenet-5 一、前言 卷积神经网络–AlexNet(最牛)-2012 Lenet-5-大规模商用(1989) 二、…...

AI Infra简单记录
向量数据库的作用 1. 在AI大模型训练过程中,向量数据库可以有效提升数据检索、特征提取等任务的效率。 2、在AI大模型推理过程中,向量数据库为大模型提供外挂知识库,提升模型时效性与准确性,提供缓存能力,减少调用开…...

三英战吕布 | 第5集 | 温酒斩华雄 | 竖子不足与谋 | 三国演义 | 逐鹿群雄
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 📌这篇博客分享的是《三国演义》文学剧本第Ⅰ部分《群雄逐鹿》的第5️⃣集《三英战吕布》的经典语句和文学剧本全集台词 文章目录 1.经典语句2.文学剧本台…...

【C语言】自定义类型:结构体
目录 1. 结构体类型的声明 1.1. 结构的一般声明 1.2. 结构的特殊声明 2. 结构体变量的创建和初始化 3. 结构体的自引用 4. 结构体内存对齐 4.1. 对其规则(面试考点) 4.2. 为什么存在内存对齐? 4.2.1. 平台原因(移植…...
算法金 | 决策树、随机森林、bagging、boosting、Adaboost、GBDT、XGBoost 算法大全
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 决策树是一种简单直观的机器学习算法,它广泛应用于分类和回归问题中。它的核心思想是将复杂的决策过程分解成一系列简单的决…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
