数据结构-分析期末选择题考点(排序)
何似清歌倚桃李
一炉沈水醉红灯

契子 ✨
上一期给大家提供了大概会考的题型给老铁们复习的大致思路
这一期还会是一样,我将整理一下排序的题型以及解题方法给你们

由于时间还很多,我就慢慢总结吧,一天一章的样子,明天总结串、后天总结图
然后坦然的走向期末考的刑场
我们还是先来讲一下排序吧?我对这块比较熟
排序重点考快排的方法,分析时间复杂度、稳定性
考排序的话,快排是必考的,因为太重要了
如果快排还不懂的老铁,可以去看看我之前的文章:手撕快排(点击链接即刻跳转)
我们二叉树中不是还有个堆吗?我遇到的题中往往是结合排序来考的 -- 堆排序。题型大概就是初始化建堆。如果还有对堆了解还不够深刻的老铁,请看这篇文章:堆排序
然后其他的题型便是:给出一些排序考你稳定性以及时间复杂度了,这里稍微去翻一下课本就行
(1)快排(常考排完一次快排后的序列)大概率会考 == 必考
我说的都是有根据的,都是自己做到的作业题以及结合一些考试因素,所以可以选择相信我
(2)堆排序(初始化建堆)高几率
(3)时间复杂度、稳定性(感觉排序也少不了的一环)
(4)环境题 -- 给出一个案例让你选择最优排序(这个很少见,考对所有排序的概念理解,但是学校应该不会为难你吧,不放心的话可以看看)
排序的考点大概就是这些,考的不多大概就两三道打底的样子(一本正经的分析)
但是这分能捡就捡,说不定离不挂科就差这几分呢?

废话说完了,直接上题吧 ~
快排的模拟
我们把这一类题称为快排的模拟,因为方法就是画图模拟快排的实现
以30为基准,设一组初始记录关键字序列为(30,15,40,28,50,10,70) 则第一趟快速排序结果为() A、10,28,15,30,50,40,70 B、10,15,28,30,50,40,70 C、10,28,15,30,40,50,70 D、10,15,28,30,40,50,70我先教老铁们模拟一遍,在公布答案:
首先说明一下快排的常识(排序思想)吧 ~ 为了以下好讲(为了照顾小白)快排思想
任取待排序元素序列中的某元素作为 基准值 ,按照该排序将待排序集合分割成两子序列,左子序列中所有元素均 小于 基准值,右子序列中所有元素均 大于 基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
而我们之前的方法则是双指针思想:模拟两个指针 left、right 分别指向首尾位置,然后 right 先找比基准小的元素,left 再找比基准大的元素,找到后交换。重复以上步骤,直到两者相遇。在这个时候,我们的相遇点的元素与基准值进行交换这样我们的一趟快排就结束了
(觉得很空洞的可以看我之前的博客)
但是如果我们做选择题的话还有简单方法,我们就不用以上方法了,我之所以提一下以上方式只是为了让大家回顾一下快排而已,接下来我将在题目的讲解中教会大家这种方法
对于模拟题的最好解法就是画图:
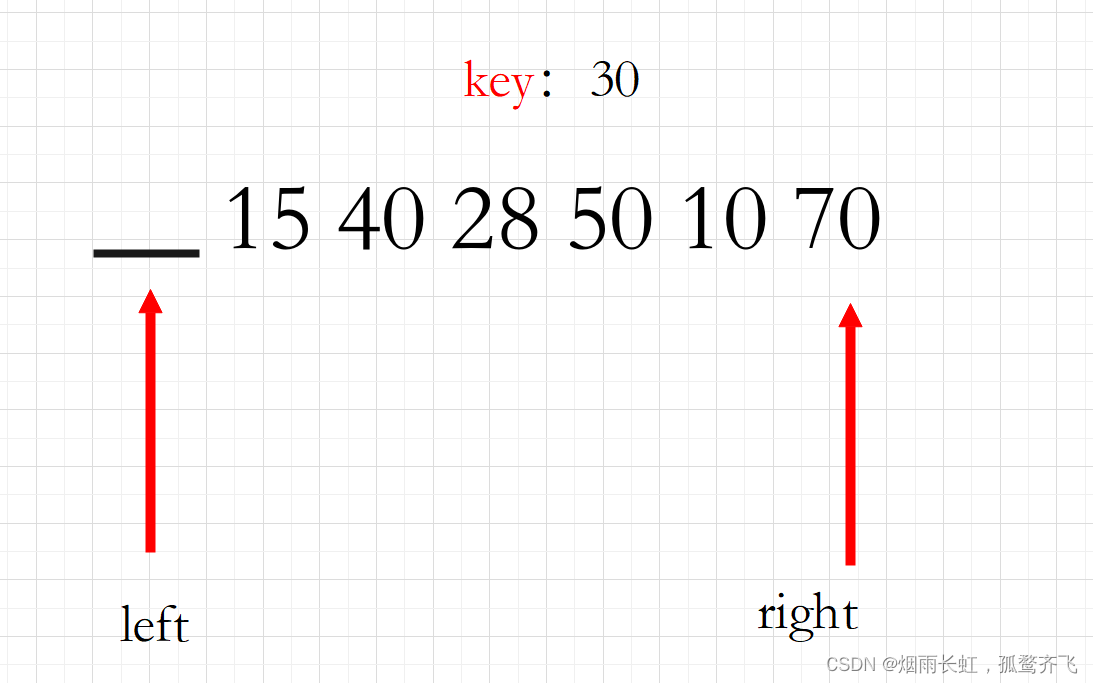
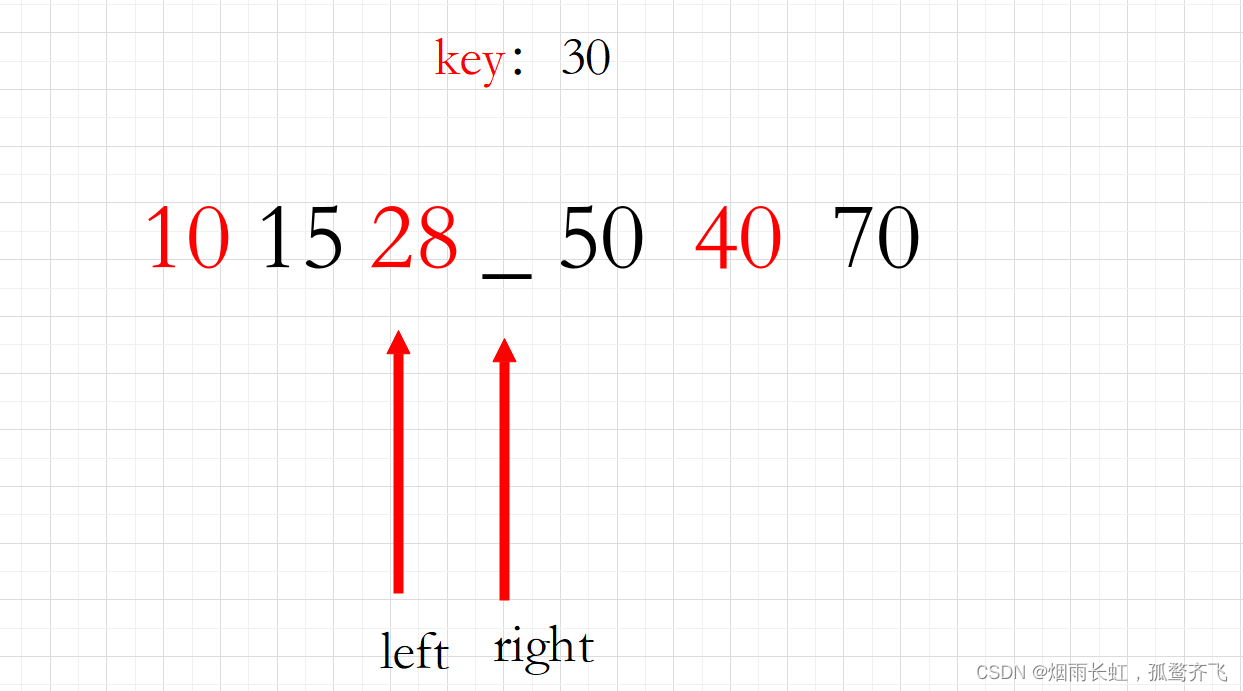
<1>根据题目的要求我们选择 30 作为基准 key,一般都是第一个位置的元素作为基准,然后我们依旧是采用双指针,也就是 left 指向剩余元素的起始位置,right 指向剩余元素的末尾位置,如下图所示:
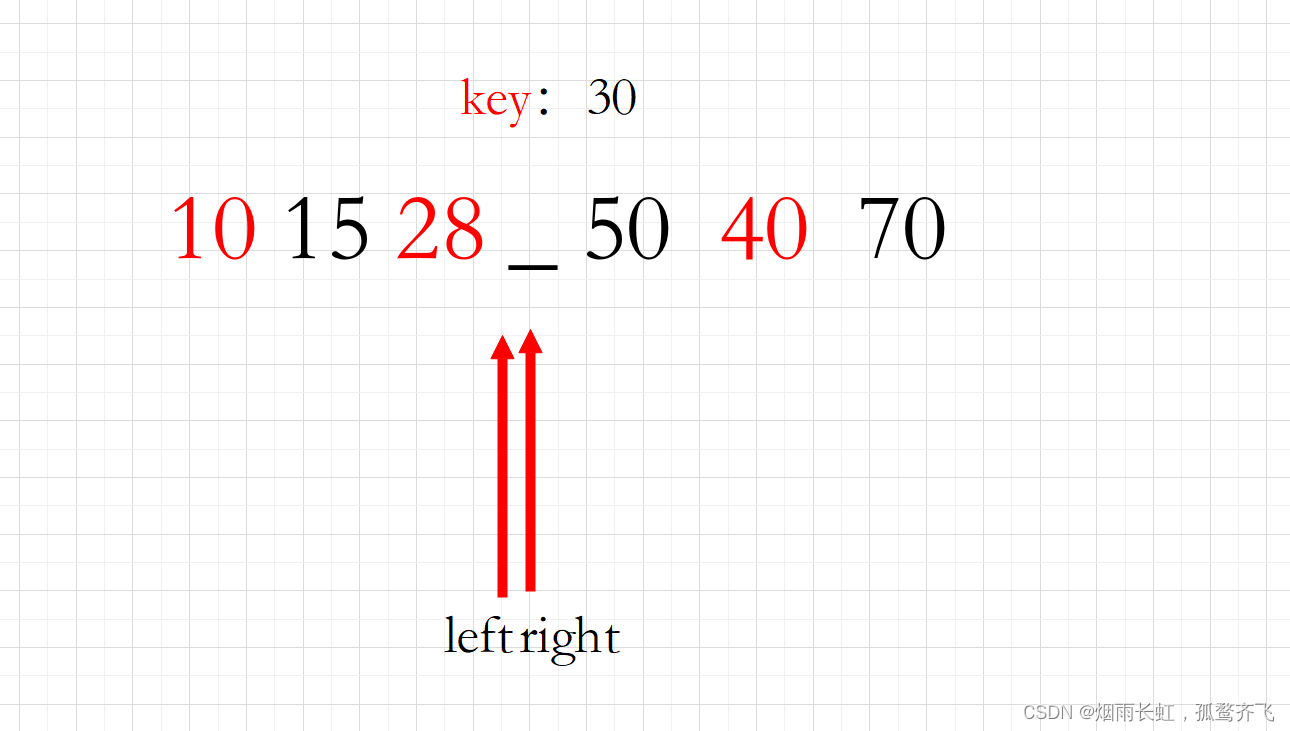
<2>我们将基准元素单独拉出来,留有一个空缺位置,像这样:
这个时候准备工作已经做完了,可以开始操作了
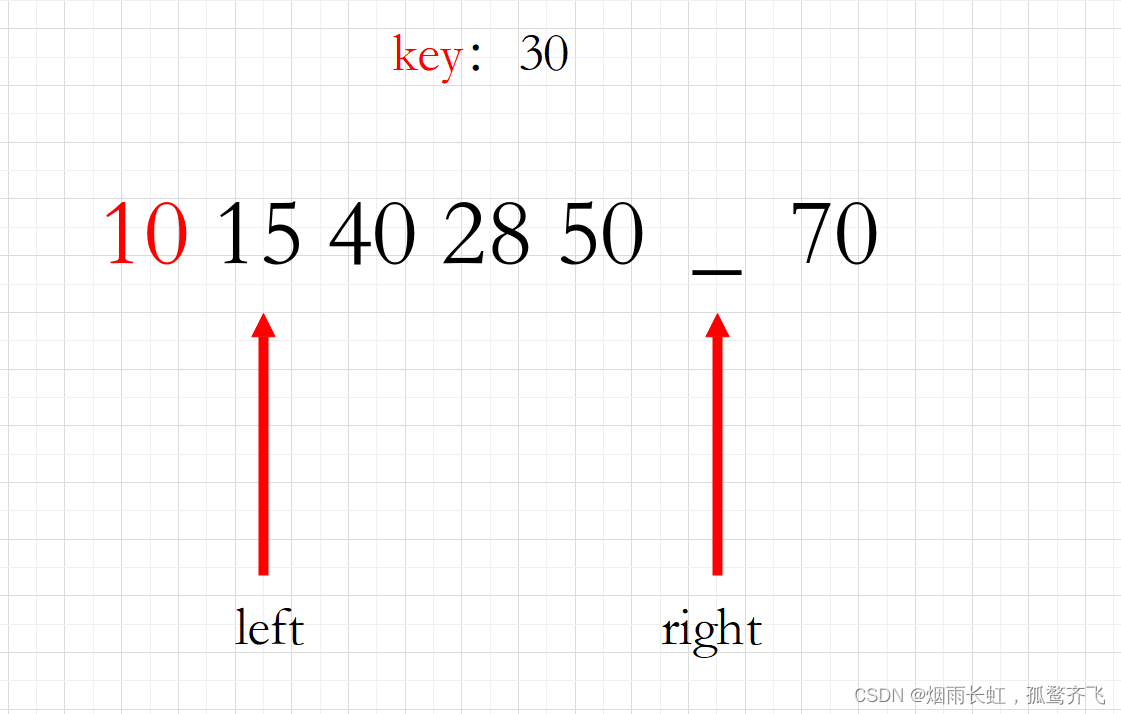
<3>我们先从右边开始找到比基准值还要小的元素
我们找到的元素是 10,就塞到那个空缺的位置中
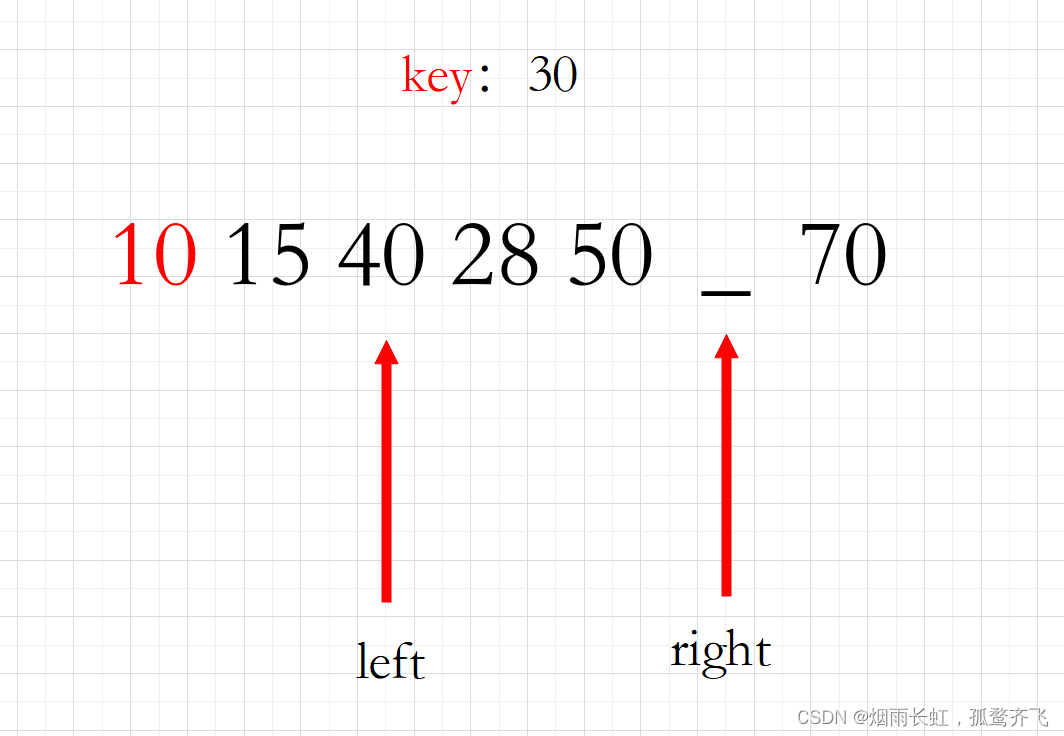
<4>其次我们从左边开始找比基准值大的元素
我们找到的是 40 也塞到空缺的位置中
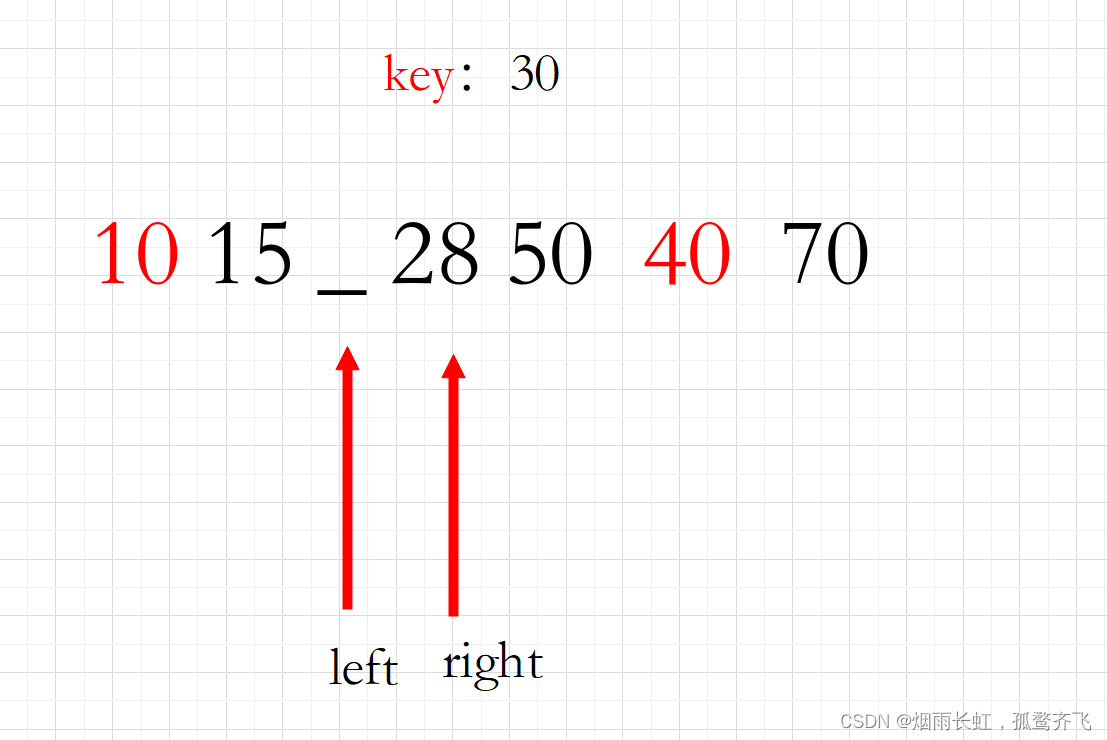
重复以上操作
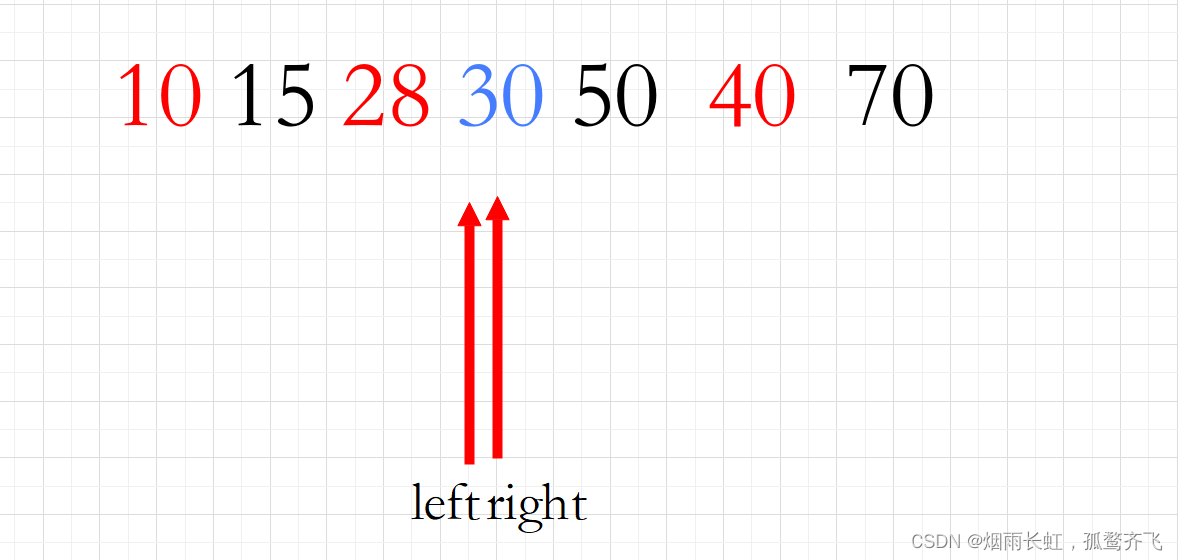
<5>当我们的双指针重叠时,就将 30 塞回空缺位置中
这样我们就完成了一趟快排,实在不知道为什么这样做的老铁先去看一下快排吧,我这里只教方法
这道题的正确答案:B
也不知道,大家对上题了解了多少,这里再提供一道
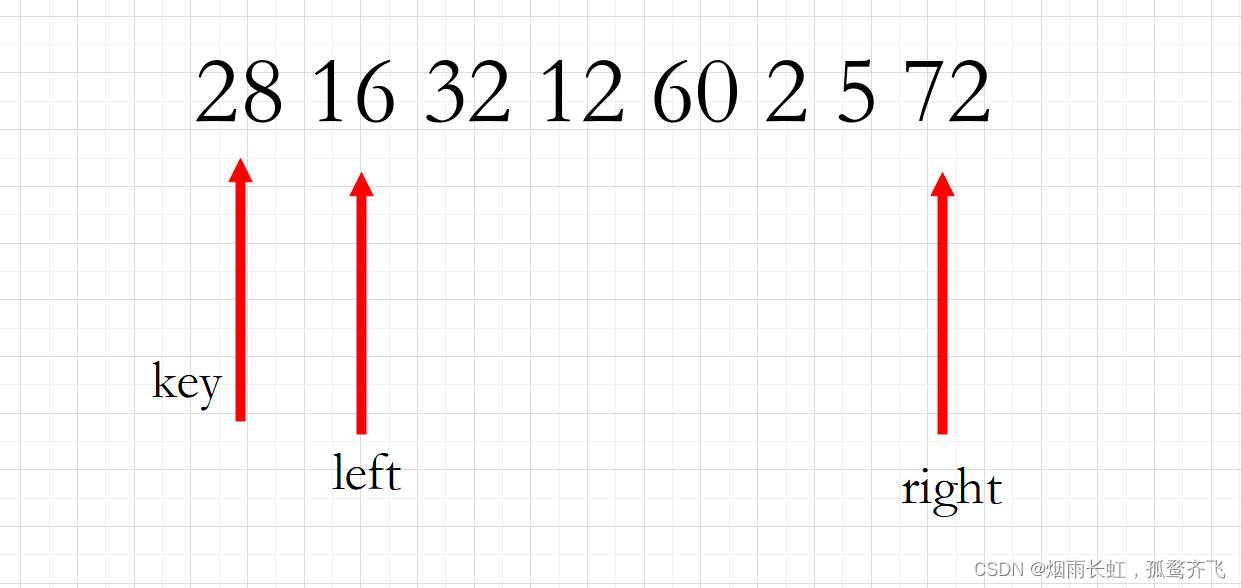
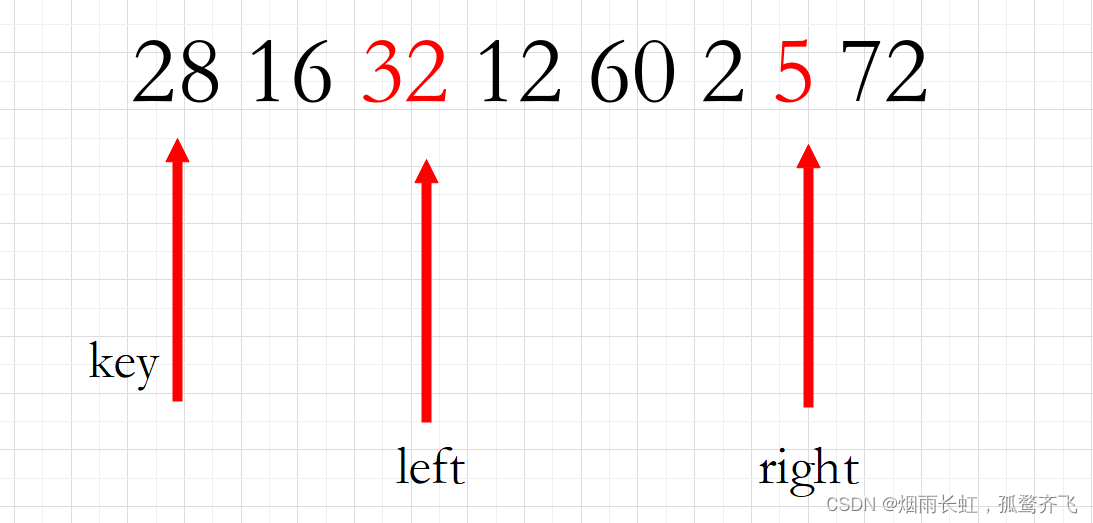
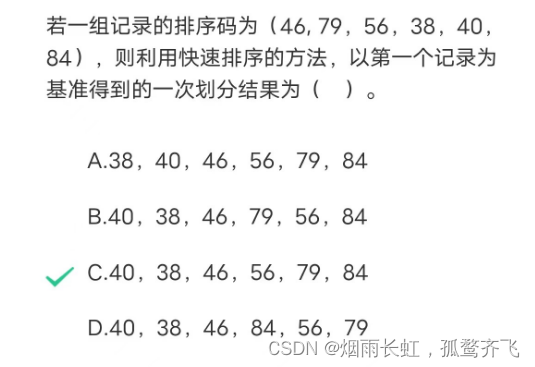
对数字序列28 16 32 12 60 2 5 72进行升序的快速排序(以第一个关键码为基准的方法) 一次划分后的结果为() A.2 5 12 16 28 60 32 72 B.2 16 5 12 28 60 32 72 C.2 16 12 5 28 60 32 72 D.5 16 2 12 28 32 60 72我们这次干脆换一种方法吧 ~ 用我们快排的原始方法:
一开始与上面那题同理,找到基准,再固定双指针
<1>右边开始先找小于基准的元素,左边再找大于基准的元素
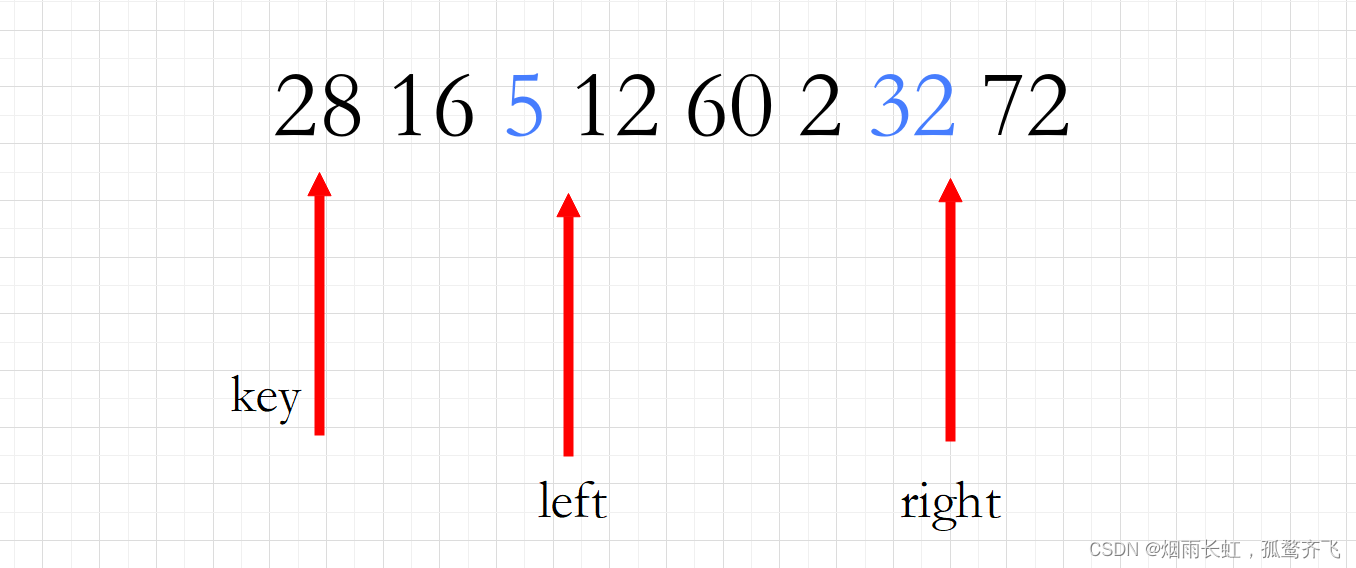
我们找到的是 5 后,左边在开始找
<2>数据都找到了便交换两者的数据
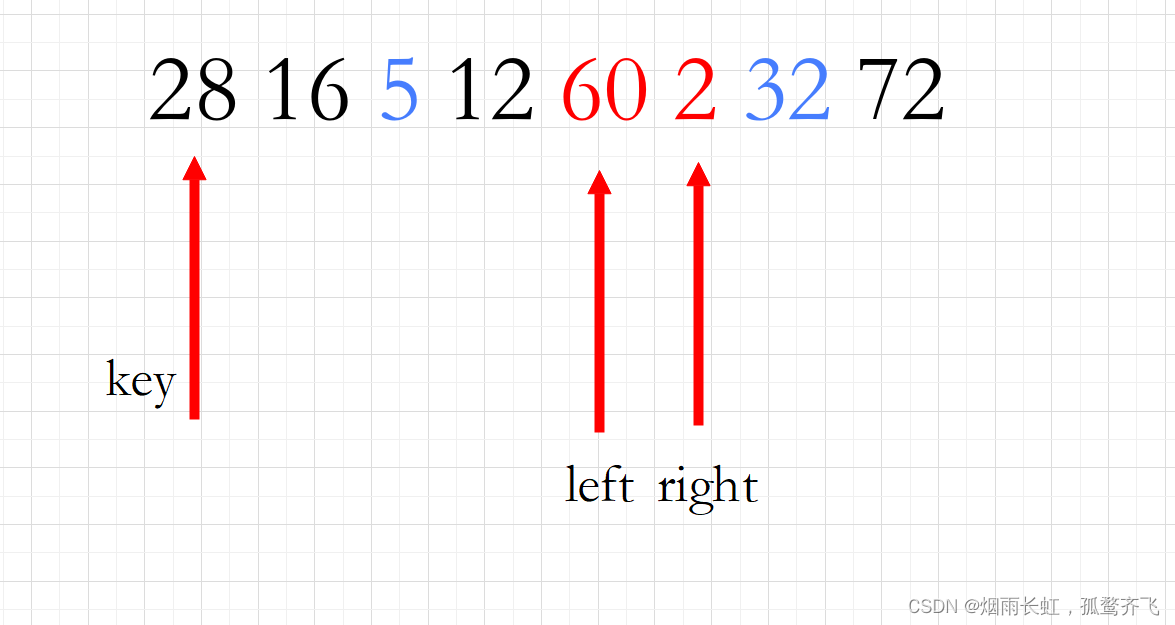
<3>重复以上步骤
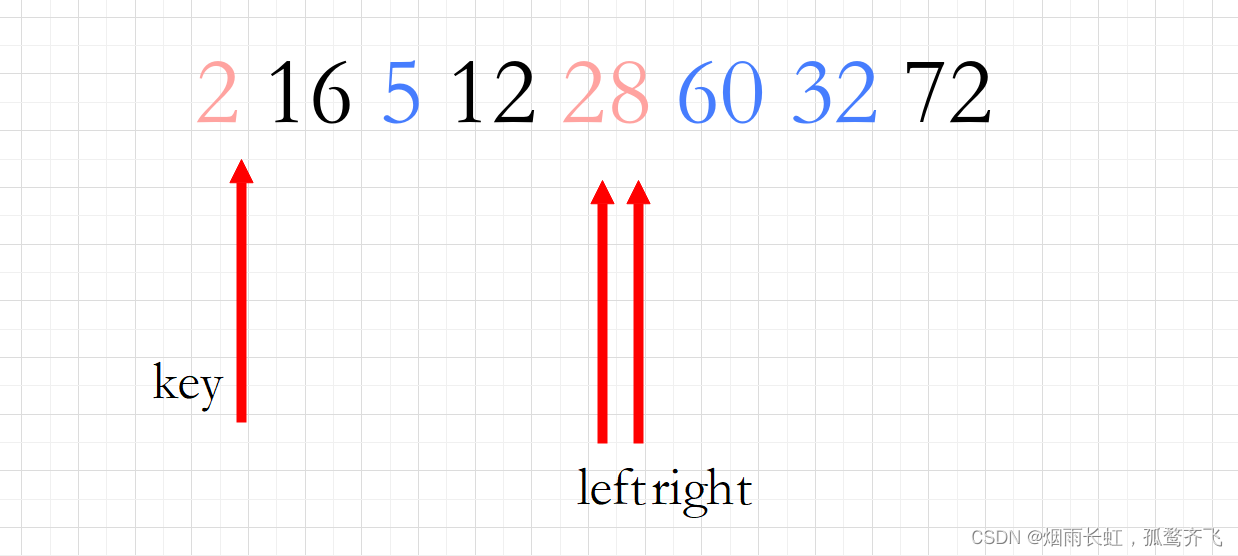
<4>当两个指针相遇时,便让当前数据与基准值 key 做交换
所以答案选择:B
解析:
快速排序以基准值为中心,对元素进行划分,这里 28 为基准值,则小于 28 的和大于 28 的进行交换,完成一次划分
这样我们的快排模拟的题型就告以段落吧,接下来我们来看看堆排序的题型
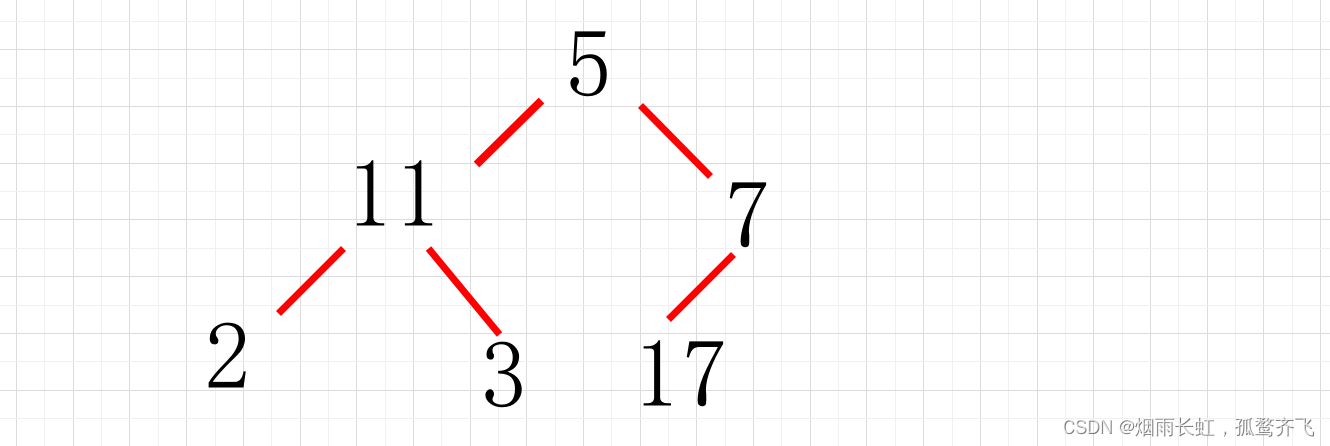
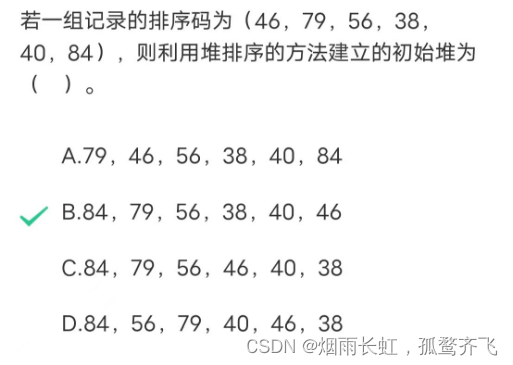
现有数字序列 5 11 7 2 3 17,目前要通过堆排序进行降序排序 那么由该序列建立的初始堆应为() A.2 3 7 11 5 17 B.17 11 7 2 3 5 C.17 11 7 5 3 2 D.2 3 5 7 11 17我们先来分析一下题目,对堆还不了解的去点上面的链接:
这里说进行降序排序,所以我们要建小堆,每次把堆顶元素放在当前堆的最后一个位置
建堆要进行向下调整算法(从最后一个非叶子节点开始进行向下调整算法,直到根元素)
我们这里就简单的模拟一下吧:
堆简单来说就是二叉树的数组表现形式,这里我们通过堆模拟一下二叉树
然后从我们的叶子节点开始,因为我们是建立小堆,那么最小的元素肯定是排在上面的
知道这个原理我们就来开始调整
因为 2 (左孩子)比 3(右孩子)小也比 11(双亲)小
所以我们就要调整 2 与 11 的位置(根据小堆原理,最小元素排在上面)
重复上面步骤开始建堆
最后我们建堆完成后便是这个样子:
然后转化为我们的数组,所以初始堆序列为: 2 3 7 11 5 17
因此答案:A
所以像这种送分题务必拿下 ~

画图题基本上已经讲完了,我们来看一下概念题 ~

下列排序算法中,占用辅助空间最多的是() A.归并排序 B.快速排序 C.希尔排序 D.堆排序答案:A
解析:
归并排序空间复杂度:n
快排: logn
希尔、堆排: 1
下列关于排序方法和其平均时间复杂度,配对错误的是() A.堆排序——O(nlog2 n) B.直接插入排序——O(n^2) C.选择排序——O(n^2) D.归并排序——O(n^2)答案:D
解析:
归并排序是二分排序,其实际复杂度为 nlogn
下列排序方法中,每一趟排序结束时都至少能够确定一个元素最终位置的方法是( )① 选择排序② 归并排序③ 快速排序④ 堆排序A.①④ B.①②④ C.①③④ D.①②③④这种题就考的是对所有排序的模拟了,需要你了解所有排序的实现原理,属于偏难的题目,小概率会出
答案:C
解析:
(1)选择排序每次选一个最值,放在最终的位置
(2)快速排序每次基准值的位置也可以确定
(3)堆排序每次堆顶元素的位置也可以确定
所以这三种方法都可以每次至少确定一个元素的位置
(4)归并排序每次都需要对 n 个元素重新确定位置,所以不能保证每次都能确定一个元素位置,有可能每次排序所有元素的位置都为发生变化
下列排序方法中,哪一种是不稳定的() A.直接插入排序 B.归并排序 C.选择排序 D.冒泡排序答案:C
解析:
(1)直接插入一般可以从前向后进行元素的插入,相同元素的相对位置可以不发生变化
(2)归并也可以保证相对位置不变
(3)冒泡排序在元素相同的情况下也可以不进行交互,也可以保证稳定
(4)选择排序的思想是每次选出最值,放在已排序序列的末尾,如果最值有多个,而选出的为最后一个最值,会导致相对位置发生变化
下列关于归并排序的说法中正确的是() A.归并排序不需要辅助空间 B.归并排序的时间复杂度是O(logn) C.归并排序是稳定排序 D.归并排序的操作方式类似二叉树的前序遍历答案:C
解析:
(1)归并排序需要一个辅助空间暂时保存部分区间的排序元素
(2)归并排序是一种二分排序算法,每次都需要给 n 个元素排序,排序的过程需要 logn,即树的高度,所以时间复杂度为 nlogn
(3)归并排序中,相同元素的相对位置不会发生变化,所以是稳定排序

本期就介绍到这里吧,排序的话应该考的不多,但是快排必考(经验+直觉)
我们下期再见 ~
相关文章:

数据结构-分析期末选择题考点(排序)
何似清歌倚桃李 一炉沈水醉红灯 契子 ✨ 上一期给大家提供了大概会考的题型给老铁们复习的大致思路 这一期还会是一样,我将整理一下排序的题型以及解题方法给你们 由于时间还很多,我就慢慢总结吧,一天一章的样子,明天总结串、后天…...

Python:探索高效、智能的指纹识别技术(简单易懂)
目录 概括 导入库 函数一 参数: 函数二 函数三 主函数 运行结果 src: model_base 7.bmp 编辑 总结 概括 指纹识别是一种基于人体生物特征的身份验证技术。它通过捕捉和分析手指上的独特纹路和细节特征,实现高准确度的身份识别。…...

『SD』AI绘画,不会写提示词怎么办?
提示词 有没有想过,为什么你用 SD 生成的猫是长这样的。 而其他人可以生成这样的猫。 虽然生成的都是猫,但猫与猫之间还是有差距的。 如果你的提示词只是“cat”,那大概率就会出现本文第一张图的那个效果。而如果你加上一些形容词ÿ…...

搭建大型分布式服务(四十二)SpringBoot 无代码侵入实现多Kafka数据源整合插件发布
系列文章目录 文章目录 系列文章目录前言MultiKafkaStarter [V2.2]一、功能特性二、快速开始(生产端)三、快速开始(消费端)四、其它特性五、变更记录六、参考文章 前言 在分布式服务的架构演进中,消息队列作为核心组件…...

Python 学习路线及技巧
一、学习路线 1. 基础阶段 ● 学习 Python 的语法基础,如变量、数据类型、运算符、控制流等。 ● 掌握常用的 Python 标准库,如 os、sys、re、datetime 等。 ● 通过编写简单的程序来巩固基础,如计算器、字符串处理等。 2. 进阶阶段 ● 深入…...

计算机网络知识整理笔记
目录 1.对网络协议的分层? 2.TCP/IP和UDP之间的区别? 3.建立TCP连接的三次握手? 4.断开TCP连接的四次挥手? 5.TCP协议如何保证可靠性传输? 6.什么是TCP的拥塞控制? 7.什么是HTTP协议? 8…...

练习 String翻转 注册处理 字符串统计
p493 将字符串中指定部分进行翻转 package chapter;public class reverse {public static void main(String[] args) {String str "abcdef";str reverseMethod(str,0,3);System.out.println(str);}public static String reverseMethod(String str, int start, in…...
linux的常用系统维护命令
1.ps显示某个时间点的程序运行情况 -a :显示所有用户的进程 -u :显示用户名和启动时间 -x :显示 没有控制终端的进程 -e :显示所有进程,包括没有控制终端的进程 -l :长格式显示 -w :宽…...

java:aocache 0.4.0 缓存控制机制
aoocache发布第一个版本0.1.0时,没有考虑到使用aocache的项目对方法缓存的控制需求。 场景 给同事做培训时,同事提到这个需求,他希望能够有方法主动去清理指定方法的缓存: 他的数据是由其他服务启动时提供的,他的方法…...

试析C#编程语言的特点及功能
行步骤,而不必创建新方法。其声明方法是在实例化委托基础上,加一对花括号以代表执行范围,再加一个分号终止语句。 2.3.3 工作原理 C#编译器在“匿名”委托时会自动把执行代码转换成惟一命名类里的惟一命名函数。再对存储代码块的委托进行设…...

Textual Learning2 -- 使用时的小问题
1、出现的问题: 在vscode里面直接运行函数会显示报错: 我尝试在vscode中含textual库的环境下运行,但仍然报错 2、解决方案: 在命令行中运行: 首先按winR,输入cmd打开命令行 或在已经安装的conda环境&a…...

CST--如何在PCB三维模型中自由创建离散端口
在使用CST电磁仿真软件进行PCB的三维建模时,经常会遇到不能自动创建离散端口的问题,原因有很多,比如:缺少元器件封装、开路端口、多端子模型等等,这个时候,很多人会选择手动进行端口创建,但是&a…...

C++中的虚函数表结构框架
一.虚函数表介绍 Virtual Table虚函数表是实现多态的 每个有虚函数的类的实现,都有个指向虚函数的指针表(不管是父类还是子类) 指向虚表的指针是作为数据成员存在实例对象中 当调用虚函数时,就去查找对象的虚表中指向整顿派生类函…...

【ES】--Elasticsearch的高亮模式
目录 一、高亮策略1、Fast Vector Highlighter(快速向量高亮器)2、Posting Highlighter(帖子高亮器)3、Unified Highlighter(统一高亮器)4、Plain Highlighter(普通高亮器)5、总结二、高亮参数三、高亮案例解析1、words_one配置解析2、words_two配置解析3、words_three…...
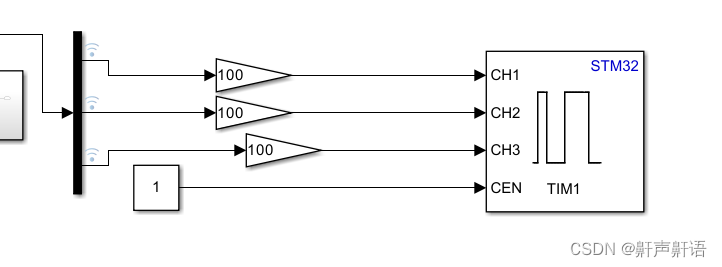
使用matlab开发stm32总结,stm32-matlab常见的问题处理以及报错合集
1,问题:本来是好的,突然编译运行报错,说是确少包, 解决方案:重启以后好了 2,有完美的马鞍波,为什么不能够转动呢? 原因是我这里模型的问题,我计算出来的是占…...

落石滑坡监测报警系统:创新保障高速公路安全
在现代交通建设中,高速公路的安全性和稳定性至关重要。特别是易发生落石区域,如何有效预防和应对落石滑坡带来的事故成为了一项关键性挑战。为此,落石滑坡监测报警系统应运而生,它通过先进的技术手段,为高速…...

Linux开发讲课20--- QSPI
SPI 是英语 Serial Peripheral interface 的缩写,顾名思义就是串行外围设备接口,一种高速的,全双工,同步的通信总线,并且在芯片的管脚上只占用四根线,节约了芯片的管脚,为 PCB 的布局上节省空间…...

VMware ESXi 8.0U3 macOS Unlocker OEM BIOS 集成驱动版,新增 12 款 I219 网卡驱动
VMware ESXi 8.0U3 macOS Unlocker & OEM BIOS 集成驱动版,新增 12 款 I219 网卡驱动 VMware ESXi 8.0U3 macOS Unlocker & OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版) 发布 ESXi 8.0U3 集成驱动版,在个人电脑上运行企业级工作负载 请访…...
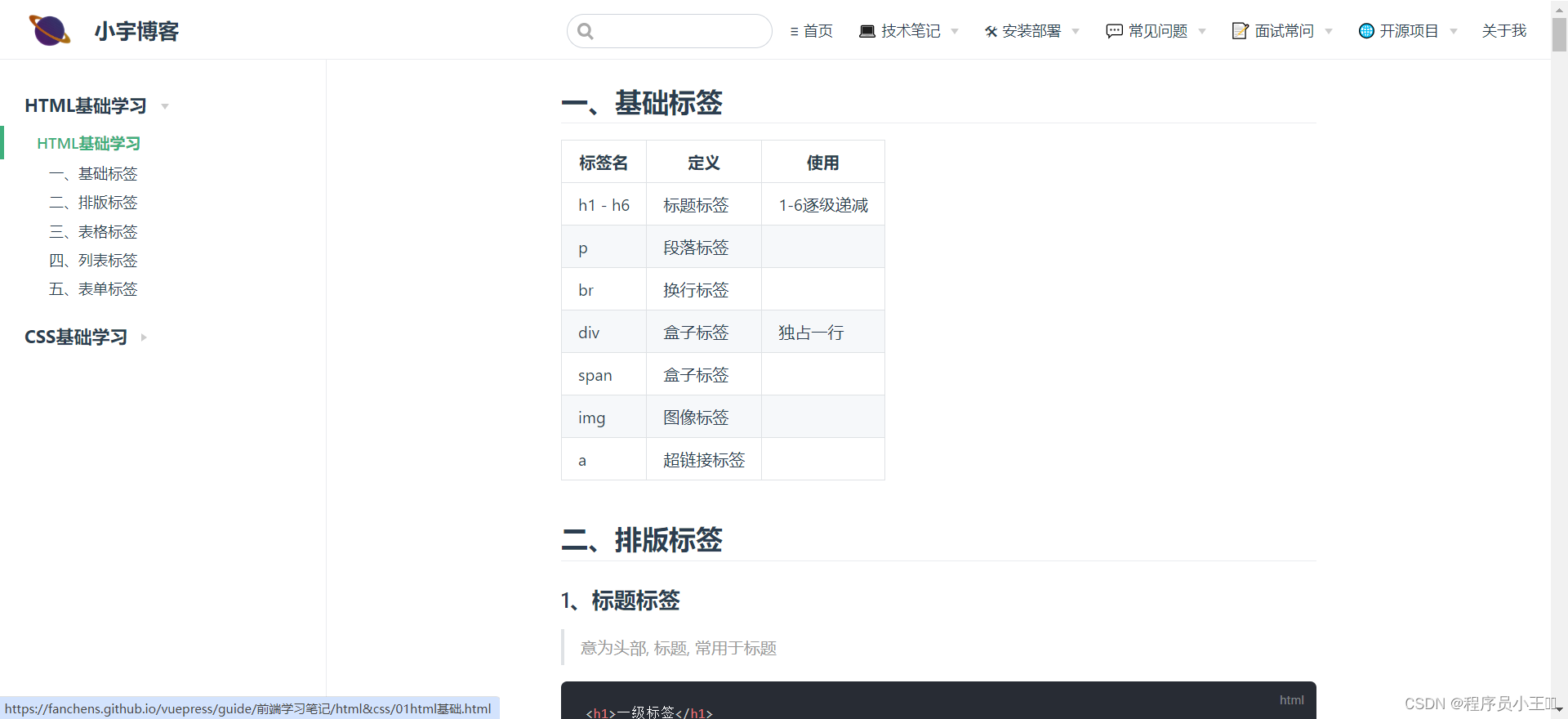
vuepress使用简介及个人博客搭建
目录 一、介绍二、环境准备三、安装运行vuepress四、目录结构五、配置文件六、导航栏配置七、导航栏logo八、浏览器图标九、侧边栏配置十、添加 Git 仓库和编辑链接十一、部署到GitHub十二、搭建成功 一、介绍 VuePress 是 Vuejs 官方提供的一个是Vue驱动的静态网站生成器&…...

c#文件读写
1.1读取文件 方法说明File.ReadAllText(FilePath);读取指定路径的文件File.ReadAllText(FilePath, Encoding);通过指定编码格式来读取指定文件File.ReadAllBytes();读取二进制文件,并把内容读取到一个字节数组File.ReadAllLines();以行的形式读取文…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...