数位DP——AcWing 1081. 度的数量
数位DP
定义
数位DP是一种动态规划技巧,特别适用于处理与数字的位操作相关的问题,如数字序列的计数、数字的生成等问题。它通过将问题分解为对每一位数字的独立考虑,从而简化问题复杂度,实现高效求解。
数位DP的核心思想是将原问题转化为对每一位数字进行决策的过程,利用动态规划的思想,从最低位向最高位(或相反)逐位考虑,每一步决策都基于当前已经确定的位数的信息。在这个过程中,通常会用一个状态表示当前处理到哪一位以及之前决策产生的某些约束条件(如数字大小、奇偶性等),并使用一个DP数组来记录到达每个状态的有效解的数量或方案。
运用情况
- 数字序列计数:例如,计算某个区间内满足特定条件的数的个数(如:包含偶数个1的数、不包含连续相同数字的数等)。
- 数字序列生成:找出所有满足给定条件的数字序列。
- 数字组合问题:比如,给定一个数字N,求所有由N的非空子集构成的数之和。
- 数字游戏问题:如,猜数字游戏中最小猜测次数等。
注意事项
- 状态定义:清晰准确地定义DP状态是关键,通常包括当前处理的位数、已使用的数字集合或限制条件等。
- 状态转移方程:根据问题的具体条件,合理设计从一位到下一位的转移逻辑,正确计算状态之间的转移。
- 初始化与边界条件:注意DP数组的初始化,尤其是处理最高位或最低位时的特殊处理。
- 遍历顺序:根据问题的特性选择从低到高还是从高到低遍历数字位,确保状态转移的正确性。
- 剪枝:对于一些问题,合理的剪枝可以大幅度减少计算量,提高效率。
解题思路
- 明确问题:首先要明确问题的具体要求,识别出需要根据数位进行决策的点。
- 状态定义:定义DP状态,通常涉及当前处理的位数、前导零的处理、已使用数字的限制等。
- 确定DP数组维度:根据状态定义,决定DP数组的维度和大小。
- 构建状态转移方程:分析如何从前一状态转移到当前状态,这一步是数位DP中最核心的部分。
- 实现与优化:编写代码实现DP算法,同时注意优化,如剪枝、记忆化等技巧以提高效率。
- 边界与初始值处理:确保DP过程的起始状态和边界条件被正确设置。
- 回溯构造答案(如果需要):在计数之外还需要具体方案时,需要根据DP过程回溯构造出满足条件的数字序列。
AcWing 1081. 度的数量
题目描述
AcWing 1081. 度的数量 - AcWing

运行代码
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 35;int l, r, k, b;
int a[N], al;
int f[N][N];int dp(int pos, int st, int op) //op: 1=,0<
{//枚举到最后一位数位,是否恰有k个不同的1(也是递归的终止条件)if (!pos) return st == k;//记忆化搜索,前提是不贴着上界(可以枚举满这一位所有的数字)if (!op && ~f[pos][st]) return f[pos][st];//01数位dp,贴着上界时,本轮能枚举的最大数就是上界数位的数字和1之间的最小值int res = 0, maxx = op ? min(a[pos], 1) : 1;for (int i = 0; i <= maxx; i ++ ){if (st + i > k) continue;res += dp(pos - 1, st + i, op && i == a[pos]);}return op ? res : f[pos][st] = res;
}
int calc(int x)
{al = 0; memset(f, -1, sizeof f); //模板的必要初始化步骤while (x) a[ ++ al] = x % b, x /= b; //把x按照进制分解到数组中return dp(al, 0, 1);
}
int main()
{cin >> l >> r >> k >> b;cout << calc(r) - calc(l - 1) << endl;return 0;
}代码思路
-
头文件引入:程序包括了
iostream、cstring和algorithm,分别用于输入输出、内存操作和算法操作。 -
常量定义:
N定义了数组的最大大小,这里设置为35,意味着可以处理的数字范围是0到10^34。 -
变量定义:定义了区间的左右边界
l和r,数字的个数k,底数b,以及用于存储数字分解的数组a和数组长度al。f是一个二维数组,用于存储中间结果,实现记忆化搜索。 -
递归函数
dp:这个函数是一个递归函数,用于计算在给定的数位pos,已经使用了st个不同的1,是否能够形成满足条件的数。参数op用于标识是否是边界条件。 -
分解函数
calc:这个函数将输入的整数x按照底数b分解,然后调用dp函数计算满足条件的数的数量。 -
主函数
main:读取输入,调用calc函数计算结果,并输出满足条件的数的数量。
改进思路
-
记忆化搜索:代码中已经使用了记忆化搜索,这有助于减少重复计算。但是,可以进一步优化记忆化搜索的逻辑,确保只存储必要的状态。
-
数组初始化:在使用
memset初始化f数组时,使用-1作为初始值,这有助于在递归过程中检查某个状态是否已经被计算过。 -
递归终止条件:在
dp函数中,递归的终止条件是pos为0,这意味着已经处理完所有的数位。这个条件是正确的,但可以进一步优化递归的逻辑,减少不必要的递归调用。 -
循环优化:在
dp函数的内部循环中,可以进一步优化循环的终止条件,避免不必要的迭代。 -
输入输出优化:虽然这个程序的输入输出操作已经很简洁,但在处理大量数据时,可以考虑使用更快的输入输出方法,比如使用
scanf和printf代替cin和cout。 -
代码可读性:代码中的变量命名可以进一步改进,以提高代码的可读性。例如,使用更具描述性的变量名,而不是单字母或缩写。
-
错误处理:程序没有包含错误处理逻辑,比如输入数据超出预期范围的情况。在实际应用中,应该添加适当的错误检查和处理。
相关文章:

数位DP——AcWing 1081. 度的数量
数位DP 定义 数位DP是一种动态规划技巧,特别适用于处理与数字的位操作相关的问题,如数字序列的计数、数字的生成等问题。它通过将问题分解为对每一位数字的独立考虑,从而简化问题复杂度,实现高效求解。 数位DP的核心思想是将原…...

2024下半年必追国漫片单,谁将问鼎巅峰?
随着2024年上半年的落幕,国漫市场再度迎来了百花齐放的盛况。从经典续作到全新IP,从玄幻到科幻,每一部作品都以其独特的魅力吸引着观众的目光。本期为大家盘点下半年值得一看的国漫佳作,大胆预测,谁将成为这场神仙打架…...
信息发布小程序h5 uniapp thinkphp
纯手工uniapp thinkphp 全开源打造 信息发布小程序 一、概述 信息发布小程序是一种基于微信平台的小程序应用,旨在为用户提供便捷的信息发布与展示服务。用户可以通过该小程序快速发布各类信息,如招聘、寻物、公告等,同时也可以浏览和搜索…...
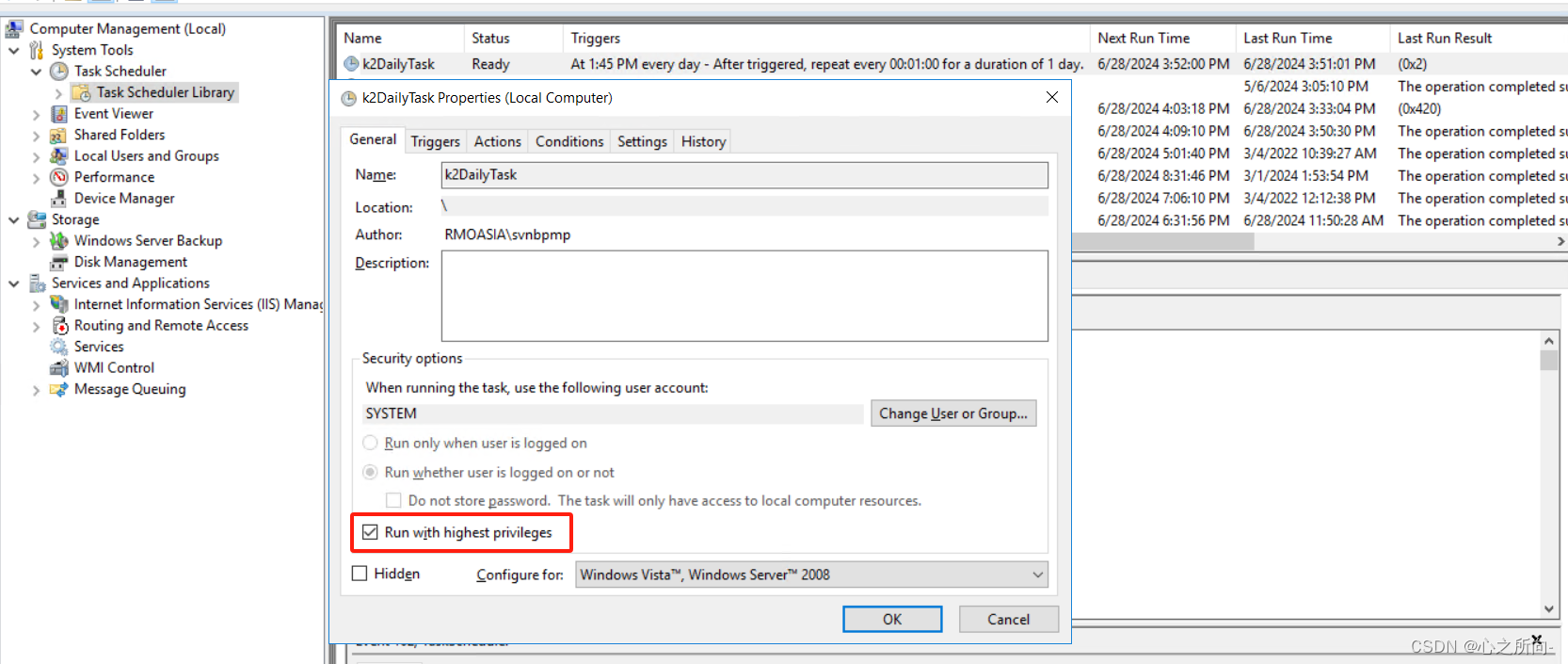
Windows定时任务执行脚本
场景:由于网络波动原因导致云数据库没连接上,从而导致某个流程引擎链接不上数据库从而导致该流程引擎服务挂了,网络恢复后 数据库链接正常,但是该引擎服务还是中止状态。 解决方案:在Windows中新建一个定时任务&#…...

优维“统一开放平台”:开放、开发、集成、客制化
基于丰富完善的产品体系,优维重磅推出了统一开放平台。这款由优维自主设计与研发,集数据开发、能力开放、能力集成、客制化为一体的统一开放平台,具备应用市场、应用开发、连接能力、采控平台、API集市、开发者工具等功能模块,可为…...

ChatGPT新纪元:揭秘GPT-4o的多模态能力
GPT-4o登场 探索ChatGPT的多模态创新 今日凌晨,OpenAI向全球宣布了AI发展的新篇章——GPT-4o,每次OpenAI发布重大更新时,尽管令人兴奋,但也不免使众多初创公司的梦想破灭。 GPT-4o的命名中的“o”象征着“omni”——全能的代表。…...

泰勒斯威夫特2022年纽约大学毕业典礼演讲:NYU‘s 2022 Commencement Speaker Taylor Swift
NYU’s 2022 Commencement Speaker Taylor Swift Link: https://www.youtube.com/watch?vOBG50aoUwlI Singer, songwriter, producer, and director Taylor Swift received a Doctor of Fine Arts, honoris causa, at the Commencement for the Class of 2022 and delivered …...
SvelteKit教程:调用外部 API 获取数据)
(四)SvelteKit教程:调用外部 API 获取数据
(四)SvelteKit教程:调用 API 我们先按照如下的方式来构建api服务: step 1:npm i json-serverstep 2:在根目录下新建 db.json 文件,内部写入如下内容:{"users": [{"id": 1,"name…...

数据结构-分析期末选择题考点(排序)
何似清歌倚桃李 一炉沈水醉红灯 契子 ✨ 上一期给大家提供了大概会考的题型给老铁们复习的大致思路 这一期还会是一样,我将整理一下排序的题型以及解题方法给你们 由于时间还很多,我就慢慢总结吧,一天一章的样子,明天总结串、后天…...

Python:探索高效、智能的指纹识别技术(简单易懂)
目录 概括 导入库 函数一 参数: 函数二 函数三 主函数 运行结果 src: model_base 7.bmp 编辑 总结 概括 指纹识别是一种基于人体生物特征的身份验证技术。它通过捕捉和分析手指上的独特纹路和细节特征,实现高准确度的身份识别。…...

『SD』AI绘画,不会写提示词怎么办?
提示词 有没有想过,为什么你用 SD 生成的猫是长这样的。 而其他人可以生成这样的猫。 虽然生成的都是猫,但猫与猫之间还是有差距的。 如果你的提示词只是“cat”,那大概率就会出现本文第一张图的那个效果。而如果你加上一些形容词ÿ…...

搭建大型分布式服务(四十二)SpringBoot 无代码侵入实现多Kafka数据源整合插件发布
系列文章目录 文章目录 系列文章目录前言MultiKafkaStarter [V2.2]一、功能特性二、快速开始(生产端)三、快速开始(消费端)四、其它特性五、变更记录六、参考文章 前言 在分布式服务的架构演进中,消息队列作为核心组件…...

Python 学习路线及技巧
一、学习路线 1. 基础阶段 ● 学习 Python 的语法基础,如变量、数据类型、运算符、控制流等。 ● 掌握常用的 Python 标准库,如 os、sys、re、datetime 等。 ● 通过编写简单的程序来巩固基础,如计算器、字符串处理等。 2. 进阶阶段 ● 深入…...

计算机网络知识整理笔记
目录 1.对网络协议的分层? 2.TCP/IP和UDP之间的区别? 3.建立TCP连接的三次握手? 4.断开TCP连接的四次挥手? 5.TCP协议如何保证可靠性传输? 6.什么是TCP的拥塞控制? 7.什么是HTTP协议? 8…...

练习 String翻转 注册处理 字符串统计
p493 将字符串中指定部分进行翻转 package chapter;public class reverse {public static void main(String[] args) {String str "abcdef";str reverseMethod(str,0,3);System.out.println(str);}public static String reverseMethod(String str, int start, in…...
linux的常用系统维护命令
1.ps显示某个时间点的程序运行情况 -a :显示所有用户的进程 -u :显示用户名和启动时间 -x :显示 没有控制终端的进程 -e :显示所有进程,包括没有控制终端的进程 -l :长格式显示 -w :宽…...

java:aocache 0.4.0 缓存控制机制
aoocache发布第一个版本0.1.0时,没有考虑到使用aocache的项目对方法缓存的控制需求。 场景 给同事做培训时,同事提到这个需求,他希望能够有方法主动去清理指定方法的缓存: 他的数据是由其他服务启动时提供的,他的方法…...

试析C#编程语言的特点及功能
行步骤,而不必创建新方法。其声明方法是在实例化委托基础上,加一对花括号以代表执行范围,再加一个分号终止语句。 2.3.3 工作原理 C#编译器在“匿名”委托时会自动把执行代码转换成惟一命名类里的惟一命名函数。再对存储代码块的委托进行设…...

Textual Learning2 -- 使用时的小问题
1、出现的问题: 在vscode里面直接运行函数会显示报错: 我尝试在vscode中含textual库的环境下运行,但仍然报错 2、解决方案: 在命令行中运行: 首先按winR,输入cmd打开命令行 或在已经安装的conda环境&a…...

CST--如何在PCB三维模型中自由创建离散端口
在使用CST电磁仿真软件进行PCB的三维建模时,经常会遇到不能自动创建离散端口的问题,原因有很多,比如:缺少元器件封装、开路端口、多端子模型等等,这个时候,很多人会选择手动进行端口创建,但是&a…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
