LeetCode:经典题之144、94、145、102题解及延伸|二叉树的遍历|前中后层序遍历|Morris算法
系列目录
88.合并两个有序数组
52.螺旋数组
567.字符串的排列
643.子数组最大平均数
150.逆波兰表达式
61.旋转链表
160.相交链表
83.删除排序链表中的重复元素
389.找不同
1491.去掉最低工资和最高工资后的工资平均值
896.单调序列
206.反转链表
92.反转链表II
141.环形链表
142.环型链表
21.合并两个有序列表
24.两辆交换链表中的节点
876.链表的中间节点
143. 重排链表
2.两数相加
445.两数相加II
目录
- 系列目录
- 前言
- 144.二叉树的前序遍历
- 94.二叉树的中序遍历
- 145.二叉树的后序遍历
- Morris遍历
- 102.二叉树的层序遍历
前言
方法都是类似的~
递归是隐式调用栈(递归栈,无需手动实现),迭代是显式调用栈
144.二叉树的前序遍历
🌟递归
原题链接
C++
若未特殊标明,以下题解均写用C++
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 注意引用符void preorder(TreeNode* root, vector<int> &res) {if (root == nullptr)// preorder 函数被定义为返回 void 类型——不返回任何值// return; 仅仅是结束函数的执行,并不返回任何值return;// 存入向量的末尾res.push_back(root->val);// 前序——根左右preorder(root->left, res);preorder(root->right, res);}vector<int> preorderTraversal(TreeNode* root) {// 定义一个 矢量/向量——更准确地说是一个动态数组vector<int> res;preorder(root, res);return res;}
};
94.二叉树的中序遍历
🌟递归+迭代
原题链接
C++
若未特殊标明,以下题解均写用C++
方法一 递归 (DFS )
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/// 二叉树的中序遍历
class Solution {
public:void inorder(TreeNode* root, vector<int>& res) {//可以另写成if (!root)if (!root) return;// 中序——左根右——先插入最左边的左孩子inorder(root->left, res);res.push_back(root->val);inorder(root->right, res);}vector<int> inorderTraversal(TreeNode* root) {vector<int> res;inorder(root, res);return res;}
};
145.二叉树的后序遍历
🌟递归+迭代
原题链接
C++
若未特殊标明,以下题解均写用C++
方法一 递归 (DFS )
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
// 二叉树的后序遍历
class Solution {
public:void postorder(TreeNode *root, vector<int> &res) {if (!root)return;// 后序——左右根postorder(root->left, res);postorder(root->right, res);// 左右都不存在才先插入根节点的值res.push_back(root->val);}vector<int> postorderTraversal(TreeNode* root) {vector<int> res;postorder(root, res);return res;}
};
方法二 迭代
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;// 空树if (!root) return res;// 定义一个 树节点栈stack<TreeNode* > stk;TreeNode *prev = nullptr;// 树没遍历完 或 栈非空while (root != nullptr || !stk.empty()) {// 树没遍历完while (root != nullptr) {// 遍历所有左节点 入栈// 将这个树节点 入栈stk.emplace(root);root = root->left;}// 若此时 root 为空// 更新 root root = stk.top();// 栈顶元素用完 弹出栈stk.pop();// 无右子节点 或 这个右子节点被遍历过if (root->right == nullptr || root->right == prev) {res.emplace_back(root->val);// 标记这个节点prev = root;root = nullptr;} // 有右子节点else { stk.emplace(root);root = root->right;}}return res;}
};
方法三 Morris遍历
class Solution {
public:void addPath(vector<int> &vec, TreeNode *node) {int count = 0;while (node != nullptr) {++count;vec.emplace_back(node->val);node = node->right;}reverse(vec.end() - count, vec.end());}vector<int> postorderTraversal(TreeNode *root) {vector<int> res;if (root == nullptr) {return res;}TreeNode *p1 = root, *p2 = nullptr;while (p1 != nullptr) {p2 = p1->left;if (p2 != nullptr) {while (p2->right != nullptr && p2->right != p1) {p2 = p2->right;}if (p2->right == nullptr) {p2->right = p1;p1 = p1->left;continue;} else {p2->right = nullptr;addPath(res, p1->left);}}p1 = p1->right;}addPath(res, root);return res;}
};
Morris遍历
Morris遍历是一种高效的二叉树遍历算法,其显著特点是能在不使用栈或队列的情况下实现中序遍历,且空间复杂度为O(1)
1. 基本思想
Morris遍历的基本思想是利用叶子节点的空指针来存储临时信息,从而达到节省空间的目的
在遍历过程中,Morris遍历会修改树中某些节点的指针指向,以便在遍历时能够方便地回溯到上一个节点 遍历完成后,需要还原树的结构
2. 实现过程
Morris遍历的实现过程可以分为以下几个步骤:
- 对于当前遍历到的节点,如果它有左子节点,就找到左子树中最右边的节点 (记为mostRight ),将其右子节点指向当前节点
- 将当前节点更新为其左子节点,继续遍历
- 如果当前节点没有左子节点,就输出当前节点的值 (或进行其他操作),并将当前节点更新为其右子节点
- 重复以上步骤,直到遍历完整棵树
3. 遍历类型
Morris遍历可以实现前序、中序和后序遍历
具体实现时,需要根据遍历的顺序调整指针的指向和节点的访问顺序
- 前序遍历:在第一次访问节点时,输出节点的值,然后进行左子树的遍历
- 中序遍历:在第二次访问节点时(即mostRight的右指针指向当前节点时),输出节点的值,然后进行右子树的遍历
- 后序遍历:后序遍历的实现相对复杂,需要在遍历过程中记录左子树最右分支的路径,并在回溯时逆序输出
4. 优缺点
- 优点:Morris遍历的空间复杂度为O(1),比使用栈或递归的遍历算法更高效
此外,Morris遍历不会占用额外的内存空间,对于内存受限的环境非常友好 - 缺点:Morris遍历会修改原始树的结构,需要在遍历完成后还原 此外,Morris遍历的实现相对复杂,需要理解其背后的思想和原理
5. 应用场景
Morris遍历适用于需要高效遍历二叉树且内存受限的场景
例如,在处理大规模数据时,使用Morris遍历可以节省内存空间并提高遍历效率
同时,Morris遍历也可以用于实现一些特殊的算法和数据结构,如线索二叉树等
102.二叉树的层序遍历
🌟BFS+队列
原题链接
C++
若未特殊标明,以下题解均写用C++
方法一 BFS
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector <vector <int>> ret;if (!root) {return ret;}queue <TreeNode*> q;q.push(root);while (!q.empty()) {int currentLevelSize = q.size();ret.push_back(vector <int> ());for (int i = 1; i <= currentLevelSize; ++i) {auto node = q.front(); q.pop();ret.back().push_back(node->val);if (node->left) q.push(node->left);if (node->right) q.push(node->right);}}return ret;}
};
方法二 队列
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
// #include <queue>
// #include <vector>
class Solution {
public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> ans; if (root == nullptr )return ans; queue<TreeNode*> cur; cur.push(root); while (!cur.empty()) {// 当前层的节点数int size = cur.size();// 存储当前层的节点值 vector<int> vals; for (int i = 0; i < size; ++i) { TreeNode* node = cur.front(); cur.pop();vals.push_back(node->val);if (node->left)cur.push(node->left); if (node->right)cur.push(node->right); } ans.push_back(vals); // 将当前层的节点值添加到答案中 } return ans; }
};
相关文章:

LeetCode:经典题之144、94、145、102题解及延伸|二叉树的遍历|前中后层序遍历|Morris算法
系列目录 88.合并两个有序数组 52.螺旋数组 567.字符串的排列 643.子数组最大平均数 150.逆波兰表达式 61.旋转链表 160.相交链表 83.删除排序链表中的重复元素 389.找不同 1491.去掉最低工资和最高工资后的工资平均值 896.单调序列 206.反转链表 92.反转链表II 141.环形链表 …...
ONLYOFFICE 桌面编辑器 8.1全新发布,更强大的编辑工具
ONLYOFFICE 8.1 一、什么是ONLYOFFICE?二、怎么安装 ONLYOFFICE 8.1三、主要功能介绍四、总结 一、什么是ONLYOFFICE? ONLYOFFICE 是一款功能强大的办公套件,旨在提供全面的文档、表格和演示文稿编辑解决方案。它集成了文字处理、电子表格和演…...

百日筑基第六天-了解一下Dubbo
百日筑基第六天-了解一下Dubbo Dubbo 是一款高性能、轻量级的开源 WEB 和 RPC 框架。 Dubbo 提供了六大核心能力: 面向接口代理的高性能 RPC 调用。智能容错和负载均衡。服务自动注册和发现。高度可扩展能力。运行期流量调度。可视化的服务治理与运维。 简单来说…...
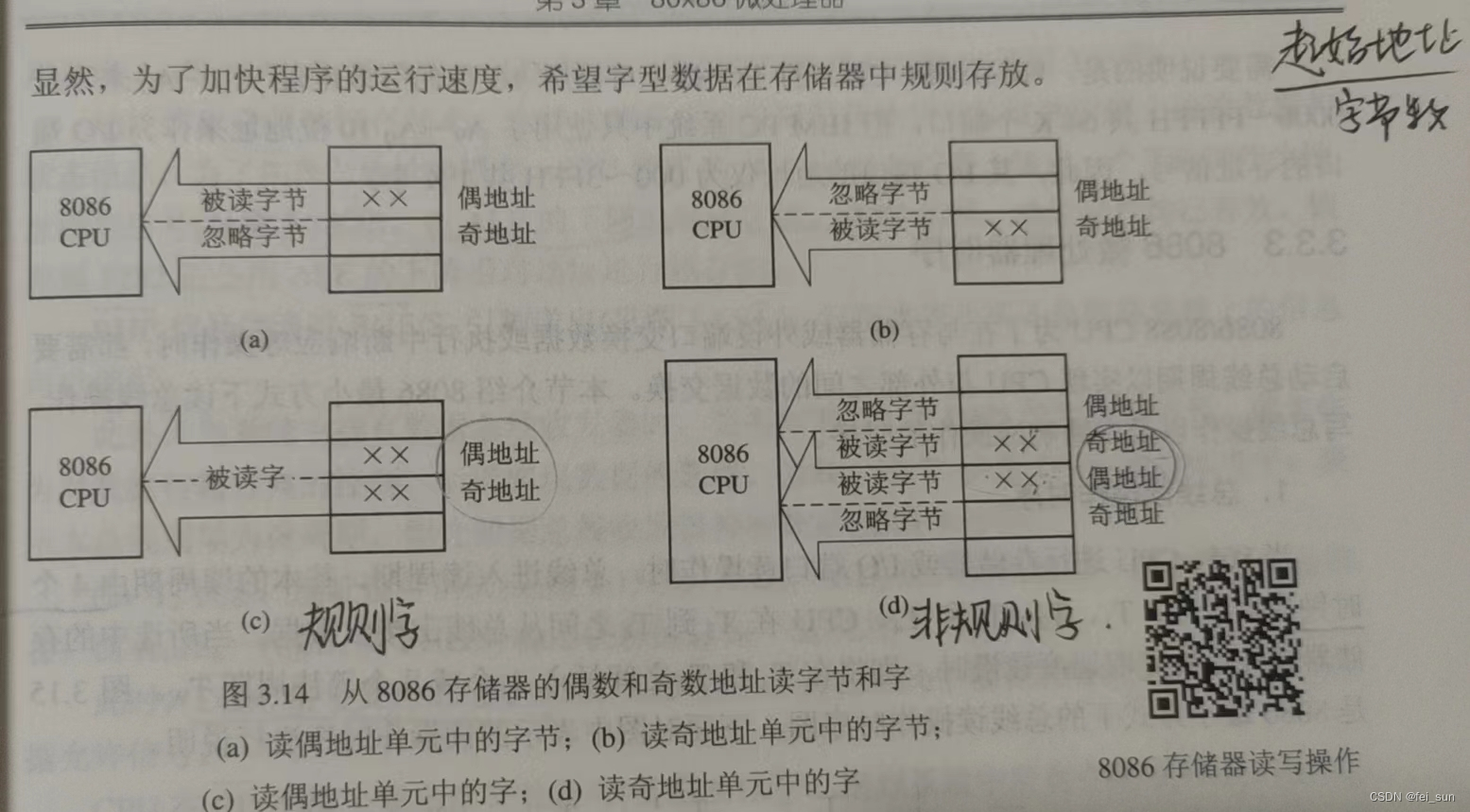
微机原理 复习
第一章导论 1.3 冯诺依曼体系结构 (1)以二进制形式表示指令和数据 (2)程序和数据事先放在存储器中(预存储) (3)由运算器、控制器、输入设备和输出设备五大部件组成 字长、主频…...

5年工作经验面试经验以及面试题分享
第一家面试题 评价 全是八股文 面试题 MySQL索引类型 索引结构 联合索引可以设置索引类型 不同索引性能差异巨大 基础索引有哪些 B Tree索引和Hash索引 Redis基本数据结构 List是原子的吗 原子性和可见性区别是什么 MySQL的存储过程和视图 MySQL性能优化有哪些 MySQL的存储…...

C# enum Enumeration Type 枚举
定义枚举使用枚举访问枚举值枚举与switch语句枚举特性枚举与位字段总结 在 C#中, enum 是一种特殊的值类型,它允许你为一组相关的常量定义一个名称。枚举提供了一种将一组整数值与更易读的名称关联起来的方法。 定义枚举 你可以使用 enum 关键字来定义…...

【ajax07基础】回调函数地狱
一:什么是回调函数地狱 在一个回调函数中嵌套另一个回调函数(甚至一直嵌套下去),形成回调函数地狱 回调函数地狱存在问题: 可读性差异常捕获严重耦合性严重 // 1. 获取默认第一个省份的名字axios({url: http://hmaj…...

华为升腾显卡选型备忘
目录 1. 开发套件 2. 加速模块 3. 加速卡 4. 训练卡 官方地址:https://www.hiascend.com/ 备注: (1)V后缀的都是Video视频解析卡,本质是推理卡; (2)I后缀的都是推理卡&#…...

Interview preparation--elasticSearch正排索引原理
正排索引 ElastciSearch 适合做或者说擅长做全文检索,在做全文检索的时候,他会通过生成倒排索引的方式来辅助查询,生成一个词项到 文档id的一个倒排表,这样直接通过 词项可以快速找到所有的 稳定信息。 但是并不是所有的搜索都是…...
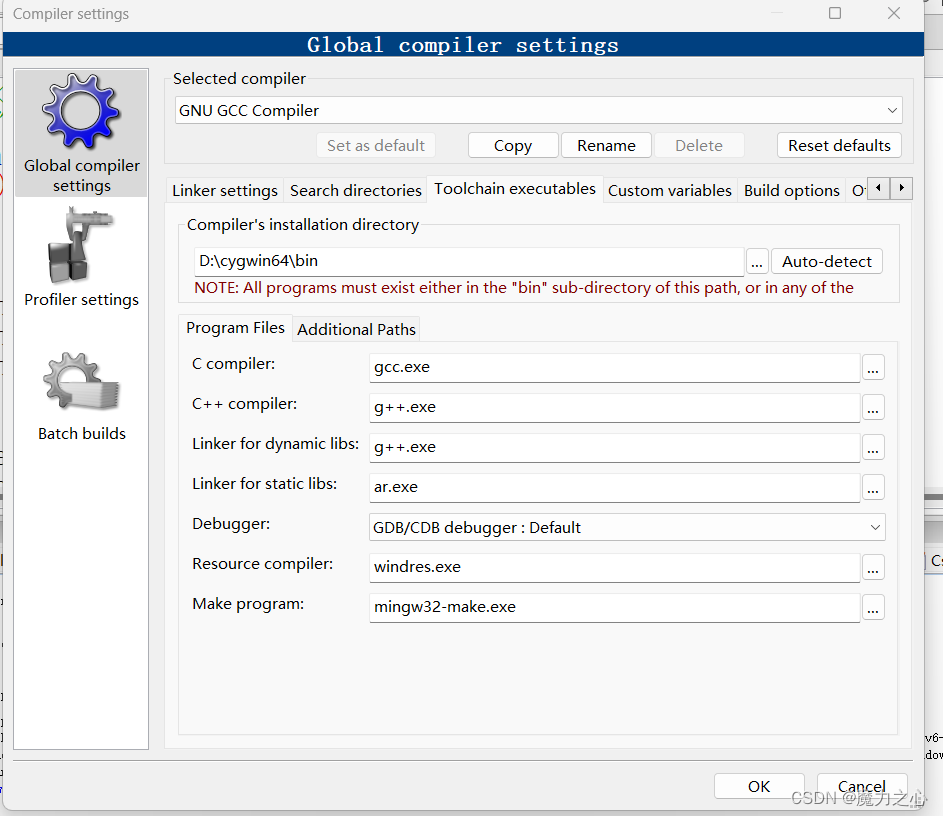
C++精解【10】
文章目录 constexpr函数GMP大整数codeblock环境配置数据类型函数类 EigenminCoeff 和maxCoeffArray类 constexpr函数 函数可能在编译时求值,则声明它为constexpr,以提高效率。需要使用constexpr告诉编译器允许编译时计算。 constexpr int min(int x, i…...
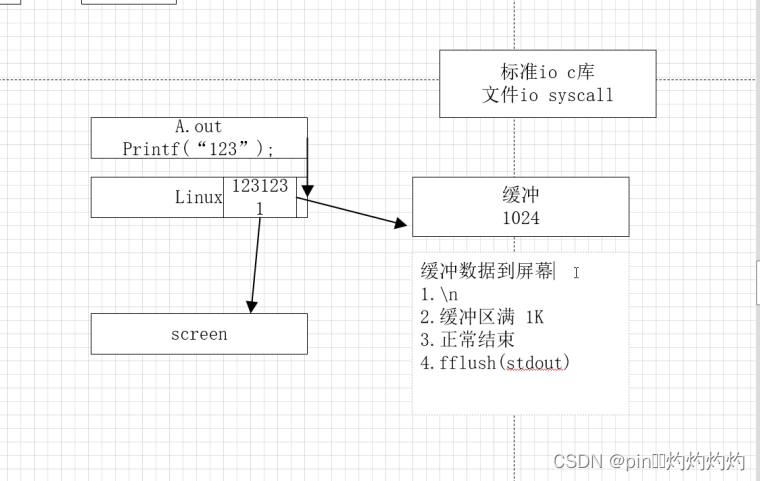
Linux高级编程——进程
1.进程的含义? 进程是一个程序执行的过程,会去分配内存资源,cpu的调度 PID, 进程标识符 当前工作路径 chdir umask 0002 进程打开的文件列表 文件IO中有提到 (类似于标准输入 标准输出的编号,系统给0,1…...

手机数据恢复篇:如何在OPPO中恢复永久删除的视频?
说到丢失重要的记忆,如何在OPPO设备中恢复永久删除的视频是一个经常困扰许多用户的话题。意外删除重要视频的情况并不少见,对许多人来说,意识到它们已经消失可能很困难。但是,在正确的指导、方法和工具的帮助下,可以找…...

Obsidan插件开发
1 Obidian 开发 Obsidian 基于 Electron 框架开发,其前端主要使用了 HTML、CSS 和 JavaScript,而后端使用了 Node.js。Node.js 是基于 Chrome V8 引擎的 JavaScript 运行环境,使 JavaScript 能在服务器端运行。 在开发 Obsidian 插件时&…...

【全球首个开源AI数字人】DUIX数字人-打造你的AI伴侣!
目录 1. 引言1.1 数字人技术的发展背景1.2 DUIX数字人项目的开源意义1.3 DUIX数字人技术的独特价值1.4 本文目的与结构 2. DUIX数字人概述2.1 定义与核心概念2.2 硅基智能与DUIX的关系2.3 技术架构2.4 开源优势2.5 应用场景2.6 安全与合规性 3. DUIX数字人技术特点3.1 开源性与…...
微信小程序服务器从腾讯云迁移到阿里云出现的坑
微信小程序服务器从腾讯云迁移到阿里云出现的坑 背景 原先小程序后台服务器到期,因为之前买的是腾讯云新用户,便宜,到期后续费金额懂的都懂。就在阿里云用新用户买了个新的,遂把服务全转到了阿里云服务器上。 此时,域…...

SQL Server触发器深度解析:数据完整性的守护者
标题:SQL Server触发器深度解析:数据完整性的守护者 摘要 在SQL Server中,触发器是一种特殊的存储过程,它在特定数据库事件发生时自动执行。触发器主要用于维护数据的完整性和实施复杂的业务规则。本文将详细介绍SQL Server中触…...
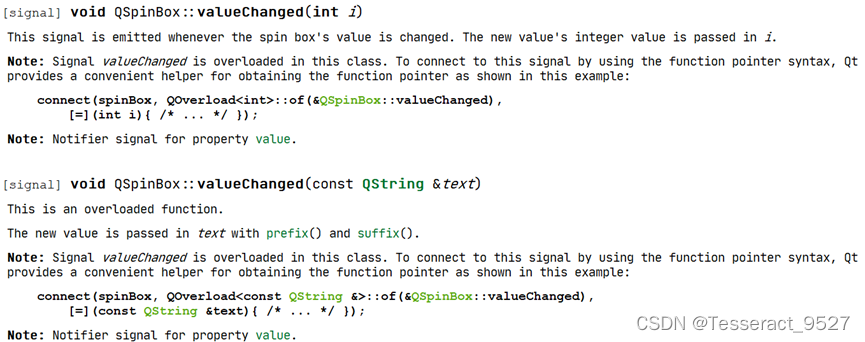
Qt信号槽的坑
1、重载的信号(以QSpinBox为例) 像是点击按钮之类的信号槽很好连接,这是因为它的信号没有重载,如果像SpinBox那样有重载信号的话(Qt5.12的见下图,不过Qt5.15LTS开始就不再重载而是换信号名了)&…...
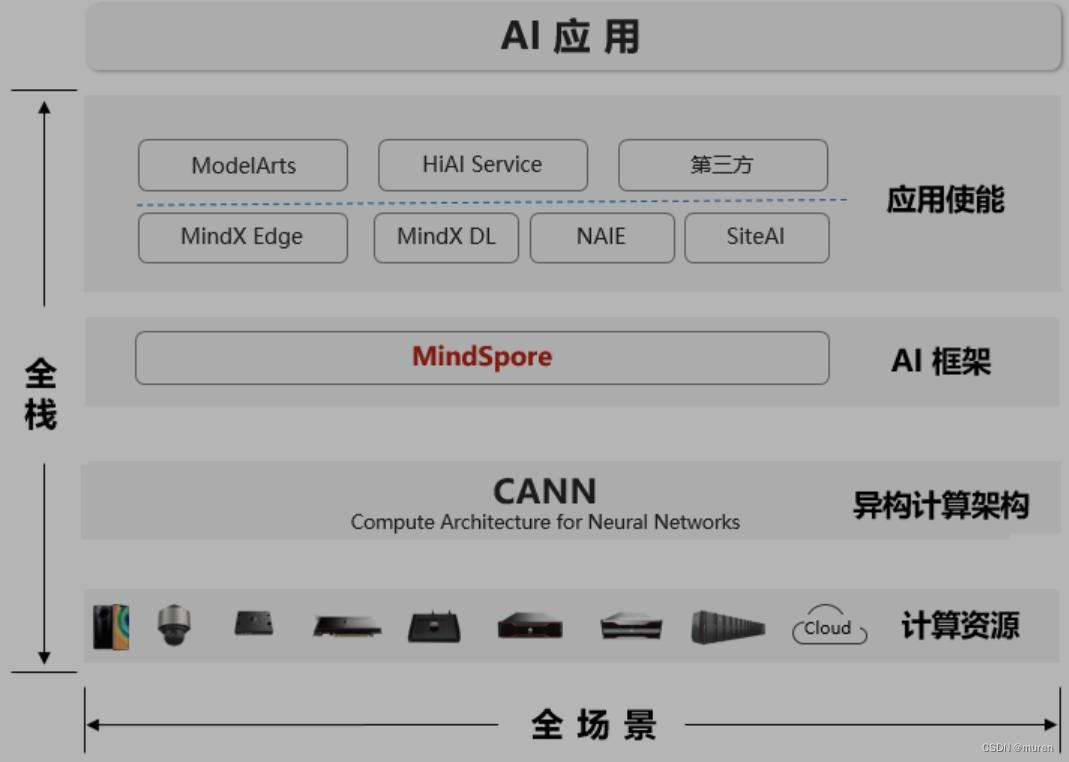
昇思MindSpore学习笔记1--基本介绍
昇思MindSpore是一个全场景深度学习框架。 一、框架组成 1. 模型库ModelZoo 提供深度学习算法网络。 2. 扩展库MindSpore Extend 拓展领域场景,如GNN/深度概率编程/强化学习等。 3. 科学计算MindSpore Science 科学计算套件。 包含数据集、基础模型、预置高精度模…...

Github Page 使用手册(保姆级教程!)
搭建个人网站?没有服务器?那不如尝试一下 Github Page ! 最近我正好在搭建个人网站,于是就写一篇博客来详细介绍 Github Page 的使用、部署方式吧! 一、进入 Github 访问:github.com 如果你没有 github…...

zram压缩机制看swapon系统调用
1.swapon开启zram交换分区 swapon /dev/block/zram0 mkswap /dev/block/zram0 上面命令调用了linux的swapon系统调用启动zram0交换分区;mkswap命令向块设备文件/dev/block/zram0写入了swap_header信息 问题:实际安卓平台是哪里触发swapon和mkswap调用的ÿ…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
