LeetCode题练习与总结:环形链表Ⅱ--142
一、题目描述
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
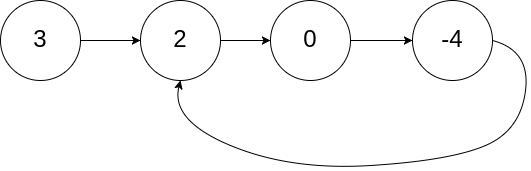
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
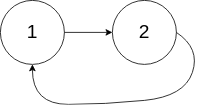
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围
[0, 10^4]内 -10^5 <= Node.val <= 10^5pos的值为-1或者链表中的一个有效索引
二、解题思路
这个问题是著名的“链表环入口”问题,可以使用“快慢指针”的解法来解决。以下是详细的解题步骤:
-
初始化两个指针,一个快指针(fast)和一个慢指针(slow),它们都从链表的头节点开始移动。
-
移动快慢指针,快指针每次移动两步,慢指针每次移动一步。
-
检查是否有环,如果快指针和慢指针相遇,则说明链表存在环。
-
寻找环的入口,当快慢指针相遇后,将其中一个指针(例如慢指针)移动到链表的头节点,另一个指针保持在相遇点。然后,两个指针以相同的速度移动,当它们再次相遇时,所在的位置就是环的入口。
-
返回结果,如果链表无环,则返回 null;如果有环,则返回环的入口节点。
三、具体代码
public class Solution {public ListNode detectCycle(ListNode head) {ListNode fast = head;ListNode slow = head;boolean hasCycle = false;// 检查是否有环while (fast != null && fast.next != null) {fast = fast.next.next;slow = slow.next;if (fast == slow) {hasCycle = true;break;}}// 如果没有环,返回 nullif (!hasCycle) {return null;}// 寻找环的入口slow = head;while (slow != fast) {slow = slow.next;fast = fast.next;}return slow; // 返回环的入口节点}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
-
检查是否有环的阶段:
- 初始化两个指针,一个快指针(每次移动两步)和一个慢指针(每次移动一步)。
- 假设链表总长度为 L,非环部分长度为 a,环部分长度为 b。
- 在没有遇到环的情况下,快指针和慢指针最多移动 L 步,即 L = a + b。
- 当快慢指针都进入环中后,它们会在环中相遇。设它们在环中相遇前,快指针比慢指针多走了 n 步,则有 n = b。
- 快慢指针相遇时,它们分别走了 a + b 和 a + b - n 步,即快指针走了 L 步,慢指针走了 L - n 步。
- 由于快指针走的步数是慢指针的两倍,所以有 2(L - n) = L,解得 n = L/2。
- 因此,慢指针在环中走了 L/2 步,快指针走了 L 步,它们相遇的时间复杂度为 O(L)。
-
寻找环的入口的阶段:
- 将慢指针移回链表头部,快指针保持在相遇点。
- 由于慢指针在环中已经走了 L/2 步,且快指针在相遇点,所以它们相遇时,慢指针走了 a 步,快指针走了 a + b 步。
- 因此,它们相遇的时间复杂度为 O(a)。
综上所述,总的时间复杂度为 O(L)。
2. 空间复杂度
- 该算法只使用了几个指针变量,没有使用额外的数据结构。
- 因此,空间复杂度为 O(1)。
五、总结知识点
-
链表操作:代码中涉及到链表的基本操作,包括遍历链表、判断节点是否为空、移动指针等。
-
快慢指针技巧:这是解决链表相关问题的一种常用技巧,通过设置两个指针,一个快一个慢,来解决问题。在本题中,快指针每次移动两步,慢指针每次移动一步,用于检测链表中是否存在环。
-
循环检测:通过快慢指针的相遇来判断链表中是否存在环。如果快慢指针相遇,则说明链表中有环;如果快指针遇到空节点,则说明链表中无环。
-
数学推理:当快慢指针在环中相遇时,通过数学推理可以得出慢指针走过的距离和环的入口之间的关系,从而找到环的入口。
-
边界条件处理:代码中需要处理链表为空或者链表没有环的情况,这需要仔细考虑边界条件,确保代码的鲁棒性。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:环形链表Ⅱ--142
一、题目描述 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测…...

【kaptcha】kaptcha验证码的使用-SpringBoot集成
Kaptcha验证码的依赖 <dependency><groupId>com.github.penggle</groupId><artifactId>kaptcha</artifactId><version>2.3.2</version> </dependency> Kaptcha验证码的配置类,对验证码的一些属性进行配置&#x…...

golang template模板嵌套语法 为何不能使用变量 底层源码解析
我们都知道在golang的模板语法中,我们可以使用template关键字嵌套其他模块, 如: {{template "模板文件名" .}} 然而,这里的 “模板文件名” 是不能使用变量的! 注意这里最后的的 . 这个实际上是templa…...
【Linux】线程Thread
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 线程概述 …...

RAG技术:在自然语言处理中的深度融合与创新
在自然语言处理(NLP)领域,随着技术的不断进步,我们见证了各种创新方法的涌现。其中,检索增强生成(Retrieval-Augmented Generation,简称RAG)技术以其独特的优势,逐渐成为…...

什么是std::bind
2024年6月29日,周日下午 std::bind 是一个C11标准库中的函数,它用于将一个函数或函数对象与特定的参数绑定在一起,生成一个新的函数对象。 std::bind通常和std::function一起使用,因为std::function可以作为一个函数容器来接收st…...
C语言的数据结构:树与二叉树(哈夫曼树篇)
前言 上篇讲完了二叉树,二叉树的查找性能要比树好很多,如平衡二叉树保证左右两边节点层级相差不会大于1,其查找的时间复杂度仅为 l o g 2 n log_2n log2n,在两边层级相同时,其查找速度接近于二分查找。1w条数据&am…...

docker 安装syslog
Syslog-ng是一个可靠、多功能的日志管理系统,用于收集日志并将其转发到指定的日志分析工具。 使用Docker CLI方式搭建 步骤 1: 拉取Syslog-ng镜像 首先,需要从Docker Hub拉取Syslog-ng的官方镜像。 docker pull balabit/syslog-ng:latest 步骤 2: 启动…...

什么是无头浏览器?
简而言之,无头浏览器是没有图形用户界面 (GUI) 的 Web 浏览器。GUI 包括用户与之交互的数字元素,例如按钮、图标和窗口。但是,关于无头浏览器,您需要了解的还有很多。 在本文中,您将了解什么是…...

【面试干货】与的区别:位运算符与逻辑运算符的深入探讨
【面试干货】&与&&的区别:位运算符与逻辑运算符的深入探讨 1、&:位运算符2、&&:逻辑运算符3、&与&&的区别 💖The Begin💖点点关注,收藏不迷路💖 & 和 …...
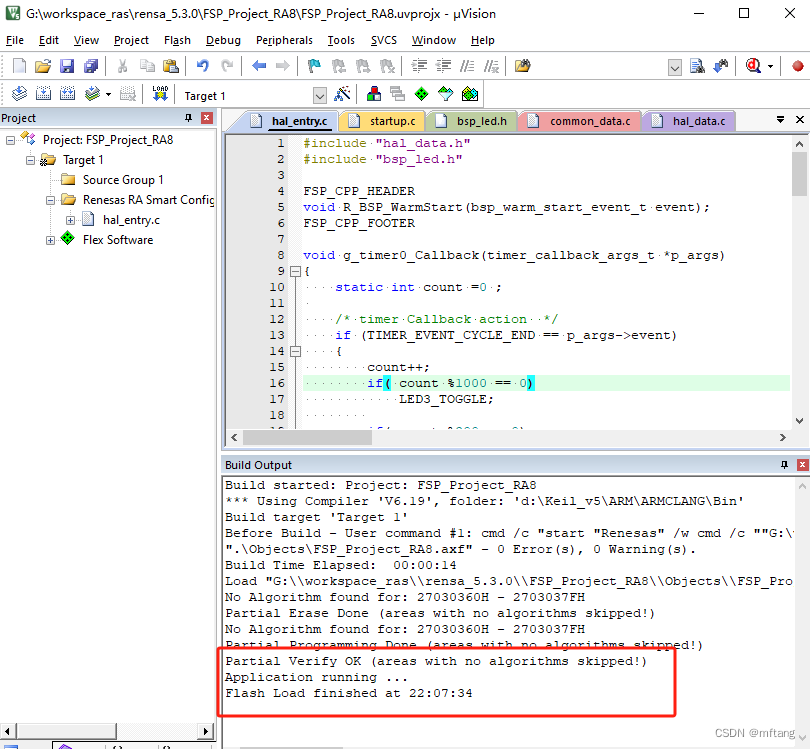
搭建Renesas R7FA8D1BHECBD-BTB的开发调试环境(DAP-LINK: N32G45XVL-STB)
目录 概述 1 软硬件 1.1 软硬件环境信息 1.2 开发板信息 1.3 调试器信息 2 FSP和KEIL产生测试项目 2.1 FSP生成项目 2.2 Keil中配置 3 硬件连接框图 4 一个测试案例 4.1 功能介绍 4.2 定时器函数 5 测试 搭建Renesas R7FA8D1BHECBD-BTB的开发调试环境(…...

探索人工智能和LLM对未来就业的影响
近年来,人工智能(AI)迅猛发展,引发了人们的兴奋,同时也引发了人们对就业未来的担忧。大型语言模型(LLM)就是最新的例子。这些强大的人工智能子集经过大量文本数据的训练,以理解和生成…...

钓鱼网站原理与攻防
知识点:LAMP平台部署,Web架构分析,钓鱼网站原理与搭建 中间件: 中间件是一种独立的软件,位于客户机和服务器之间,主要用于在网络环境中进行数据的传输和通信。它充当客户端和服务端之间的桥梁,…...
Windows 中 Chrome / Edge / Firefox 浏览器书签文件默认存储路径
1. Chrome 浏览器 按组合键 Win R,打开运行对话框,输入 %USERPROFILE%\AppData\Local\Google\Chrome\User Data\Default或在Chrome 浏览器地址栏输入 chrome://version查看【个人资料路径】 2. Edge 浏览器 按组合键 Win R,打开运行对…...

秋招Java后端开发冲刺——关系型数据库篇(Mysql)
本文介绍关系型数据库及其代表Mysql数据库,并介常见面试题目。 一、数据库概述 1. 数据库(Database, DB):是长期储存在计算机内的、有组织的、可共享的数据集合。 2. 数据库管理系统(Database Management System, D…...
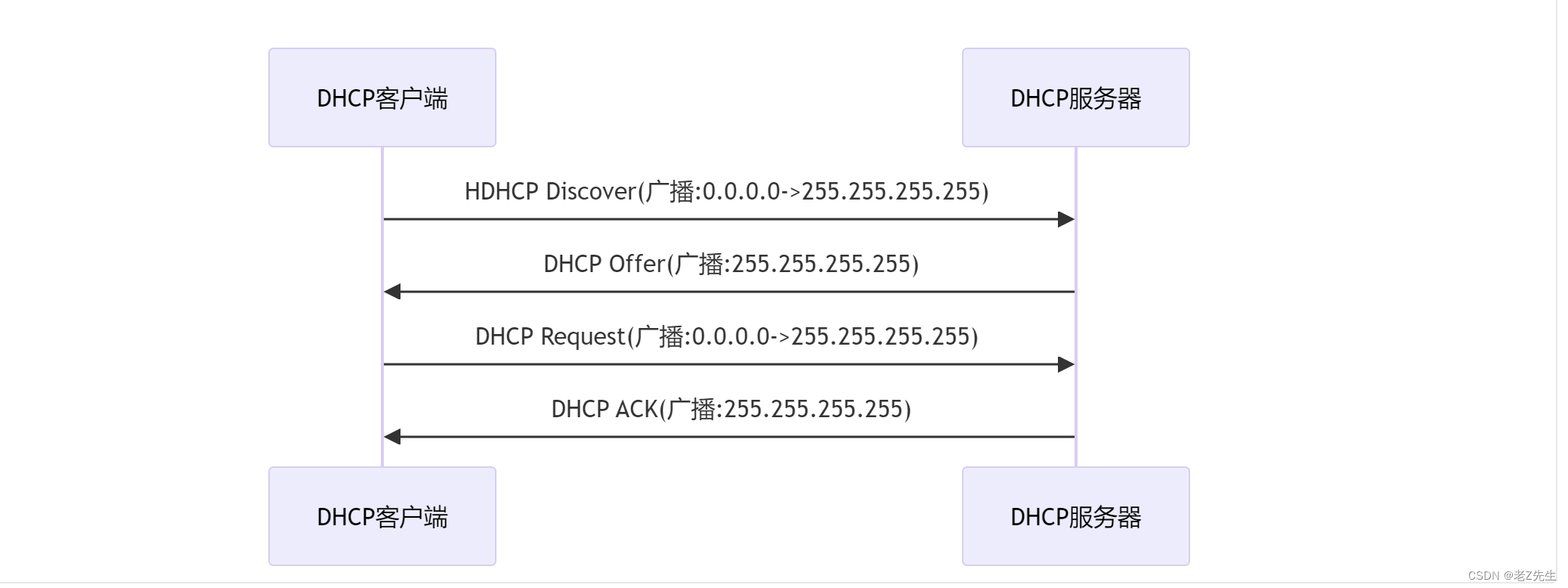
DHCP原理1-单个局域网出现多个DHCP服务器会发生什么
1. 背景 DHCP全称是Dynamic Host Configuration Protocol。其协议标准是RFC1541(已被RFC2131取代),主要实现服务器向客户端动态分配IP地址(如IP地址、子网掩码、网关、DNS)和配置信息。其系统架构是标准的C/S架构。RFC…...
程序的编译和链接)
24/06/29(21.1205)程序的编译和链接
源文件 ---> 可执行文件,这一过程要执行的流程: 预处理 编译 汇编 链接 组成每一个程序的每个源文件通过编译过程分别转换成目标代码;每个目标代码由链接器捆绑在一起,形成一个单一而完整的可执行程序;链接器同时也会引入标准函数库中任何被该程序所用到的函数,而且它可以…...

使用Java Executors框架处理并发任务
一、并发与Java Executors框架简介 一、并发编程的重要性 并发编程是现代编程中最重要的概念之一。在更多的核心和更快的处理器出现的今天,如何充分利用这些资源就变得异常重要。并发编程允许你的程序同时处理多个任务,从而使程序更有效地利用系统资源,提高执行效率。 提…...

LeetCode:经典题之144、94、145、102题解及延伸|二叉树的遍历|前中后层序遍历|Morris算法
系列目录 88.合并两个有序数组 52.螺旋数组 567.字符串的排列 643.子数组最大平均数 150.逆波兰表达式 61.旋转链表 160.相交链表 83.删除排序链表中的重复元素 389.找不同 1491.去掉最低工资和最高工资后的工资平均值 896.单调序列 206.反转链表 92.反转链表II 141.环形链表 …...
ONLYOFFICE 桌面编辑器 8.1全新发布,更强大的编辑工具
ONLYOFFICE 8.1 一、什么是ONLYOFFICE?二、怎么安装 ONLYOFFICE 8.1三、主要功能介绍四、总结 一、什么是ONLYOFFICE? ONLYOFFICE 是一款功能强大的办公套件,旨在提供全面的文档、表格和演示文稿编辑解决方案。它集成了文字处理、电子表格和演…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
