开发微信小程序从开始到部署上线,哪些个流程需要付费
1. 微信公众平台账号注册
- 费用:300元人民币(这是企业账号的认证费用,个人账号不需要付费)。
- 说明:如果你是企业或组织,需要进行微信公众平台的认证,这会产生费用。个人开发者可以免费注册账号,但某些功能可能受到限制。
2. 服务器和域名
- 费用:根据服务器和域名供应商的不同,费用差异较大。常见的选择包括阿里云、腾讯云等。
- 服务器:一般按月或按年付费,价格从几十元到几千元不等,具体取决于配置和性能需求。
- 域名:一般按年付费,价格从几十元到几百元不等。
3. 开发工具和软件
- 费用:微信开发者工具是免费的,但是其他开发辅助工具(如IDE、设计软件等)可能需要付费。
- 设计软件:如Adobe Photoshop、Sketch、Figma等,一般按月或按年付费。
- 版本控制工具:如GitHub的高级功能或私有仓库可能需要付费。
4. 第三方服务
- 费用:使用第三方服务可能会产生费用。
- 云开发服务:微信提供的云开发服务按使用量计费,包括云函数、云数据库、云存储等。
- 第三方API:如地图服务、支付服务、短信服务等,通常按调用次数或用户量计费。
5. 开发和维护人员
- 费用:如果雇佣开发人员或外包开发工作,费用将根据开发人员的技能和项目复杂度有所不同。
- 开发人员:一般按小时或按项目收费,费用从几千元到几万元不等。
- 维护和更新:上线后的小程序需要持续维护和更新,这部分费用也是持续的。
6. 小程序上线审核
- 费用:微信小程序的上线审核本身是免费的,但是在某些特定情况下(如需要特殊资质、认证等)可能会产生额外费用。
7. 市场推广
- 费用:为了让更多用户知道和使用你的小程序,可能需要进行市场推广。
- 广告投放:在微信、微博、抖音等平台进行广告投放。
- 运营活动:举办线上线下活动来吸引用户。
综上所述,从开发到部署上线,小程序的费用主要集中在账号注册、服务器和域名、开发工具、第三方服务、开发和维护人员、市场推广等环节。具体费用取决于项目的规模和需求,建议提前做好预算规划。
相关文章:

开发微信小程序从开始到部署上线,哪些个流程需要付费
1. 微信公众平台账号注册 费用:300元人民币(这是企业账号的认证费用,个人账号不需要付费)。说明:如果你是企业或组织,需要进行微信公众平台的认证,这会产生费用。个人开发者可以免费注册账号&a…...

python r, b, u, f 前缀详解
1、r前缀 一般来说,\n’是一个换行符,是一个字符串;而加上r为前缀后,不会以任何特殊方式处理反斜杠。因此,r"\n" 是包含 ‘\’ 和 ‘n’ 的双字符字符串;示例如下: >>> pr…...
Go语言简介
Go语言 Go语言是由 Google 的 Robert Griesemer,Rob Pike 及 Ken Thompson 开发的一种静态强类型、编译型语言。 Go 语言(或称 Golang)是云计算时代的C语言。Go语言的诞生是为了让程序员有更高的生产效率,Go语言专门针对多处理器系统应用程序的编程进行了优化&…...
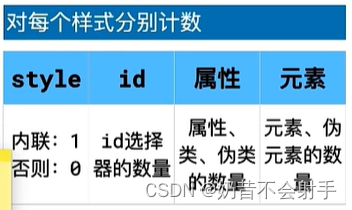
css持续学习
一、样式层叠 当一个css样式发生冲突时,比如多处给一个字体设置了不同的颜色,这个时候就需要样式层叠了,它会进行三种比较 比较重要性 重要性从高到低: 1.带有 important 的作者样式(作者样式就是开发者写的样式&…...

FFmpeg 关于AV1编码指导文档介绍
介绍 本篇博客主要介绍FFMpeg中关于AV1编码支持说明,主要根据官方wiki说明进行总结。官方wiki地址:AV1AV1是一种由Alliance for Open Media (AOMedia)开发的开源且免版税的视频编解码器,它在压缩效率上比VP9高出约30%,比H.264高出约50%。目前,FFmpeg支持三种AV1编码器:li…...
鸿蒙系统——强大的分布式系统
鸿蒙相比较于传统安卓最最最主要的优势是微内核分布式操作系统,具有面向未来,跨设备无缝协作,数据共享的全场景体验。下面简单来感受一下鸿蒙系统的多端自由流转。 自由流转概述 场景介绍 随着全场景多设备的生活方式不断深入,…...
centos7 安装单机MongoDB
centos7安装单机 yum 安装 1、配置yum源 vim /etc/yum.repos.d/mongodb.repo [mongodb-org-7.0] nameMongoDB Repository baseurlhttps://repo.mongodb.org/yum/redhat/$releasever/mongodb-org/7.0/x86_64/ gpgcheck1 enabled1 gpgkeyhttps://www.mongodb.org/static/pgp…...

数据库回表介绍
索引覆盖 索引覆盖或称为覆盖索引,是数据库中的一种优化手段当我们在执行一个sql查询时,如果只需要查询某几个字段的值,并且这几个字段的数据都已经被包含在某一个索引中(而不是全表扫描),那么数据库引擎就会直接通过这个索引来取…...
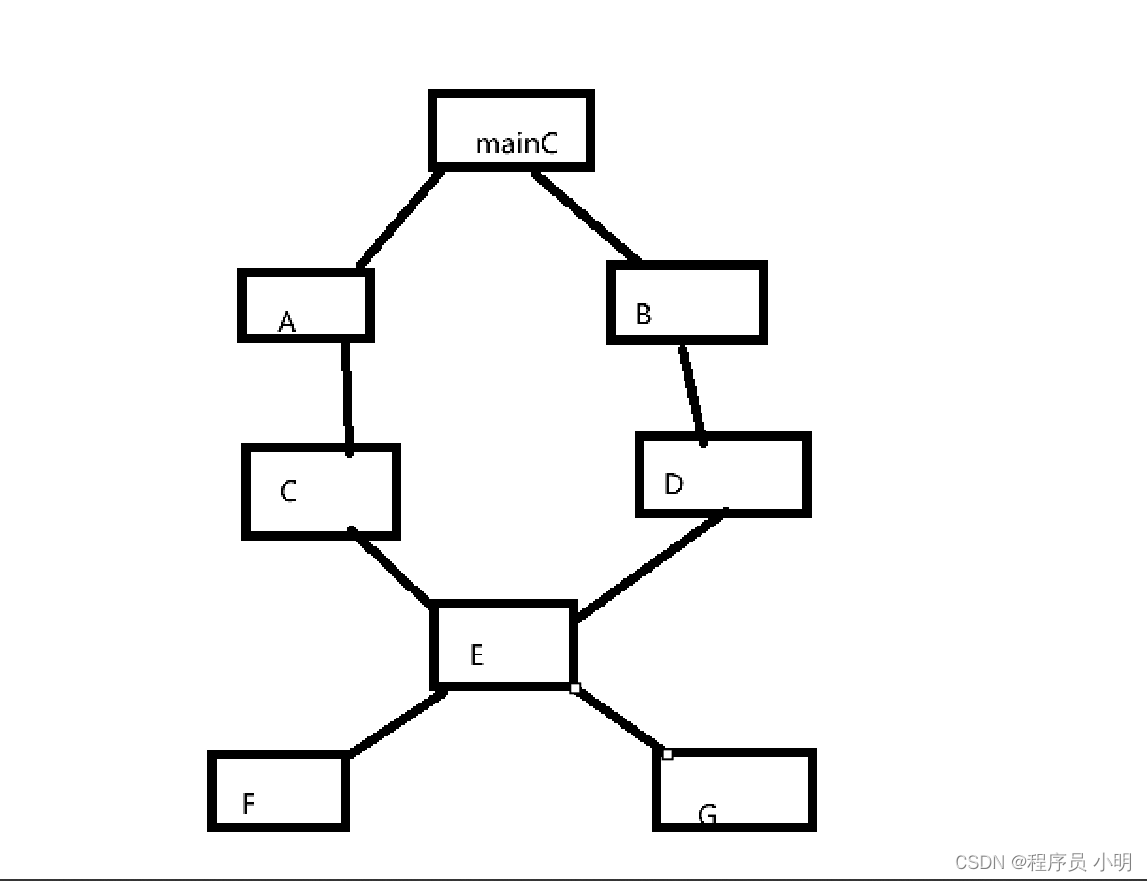
python多继承的3C算法
python多继承的3C算法 有很多地方都说python多继承的继承顺序,是按照深度遍历的方式,其实python多继承顺序的算法,不是严格意义上的深度遍历,而是基于深度遍历基础上优化出一种叫3C算法 python多继承的深度遍历 class C:def ru…...
掌握Python编程的深层技能
一、Python基础语法、变量、列表、字典等运用 1.运行python程序的两种方式 1.交互式即时得到程序的运行结果 2.脚本方式把程序写到文件里(约定俗称文件名后缀为.py),然后用python解释器解释执行其中的内容2.python程序运行的三个步骤 python3.8 C:\a\b\c.py 1.先启动python3…...
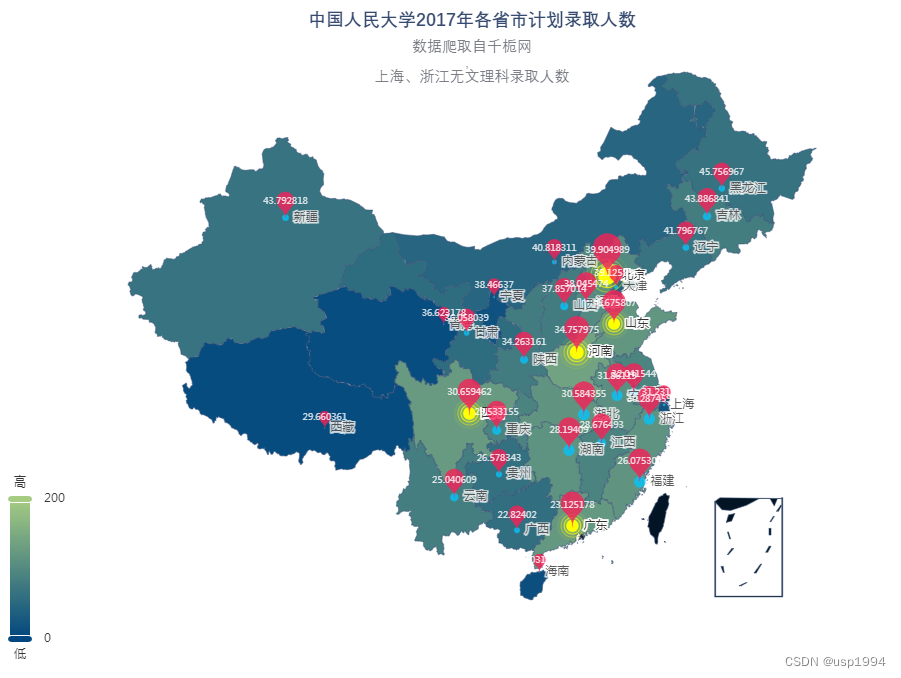
Echarts地图实现:各省市计划录取人数
Echarts地图实现:各省市计划录取人数 实现功能 本文将介绍如何使用 ECharts 制作一个展示中国人民大学2017年各省市计划录取人数的地图。我们将实现以下图表形式: 地图:基础的地图展示,反映不同省市的录取人数。散点图…...

shell脚本if/else使用示例
if判断字符串是否为空实例if判断整数是否为奇数实例if判断整数是否为偶数实例if判断整数是否为正数实例if判断整数是否为负数实例输入两个字符串,输出字符串的大小关系输入学生的成绩判断是否合法输入学生的成绩判断是否及格判断平年闰年输入文件判断文件是否是普通…...

【D3.js in Action 3 精译】1.2.2 可缩放矢量图形(二)
当前内容所在位置 第一部分 D3.js 基础知识 第一章 D3.js 简介 1.1 何为 D3.js?1.2 D3 生态系统——入门须知 1.2.1 HTML 与 DOM1.2.2 SVG - 可缩放矢量图形 ✔️ 第一部分【第二部分】✔️第三部分(精译中 ⏳) 1.2.3 Canvas 与 WebGL&#x…...

Java中的Monad设计模式及其实现
Java中的Monad设计模式及其实现 在函数式编程中,Monad是一种重要的设计模式,用于处理包含隐含计算信息(如计算顺序、环境、状态、错误处理等)的计算。Monad提供了一种结构,使得可以将计算链式连接起来,每一…...

Dahlia Hart: Stylized Casual Character(休闲角色模型)
此包包含两个发型和两个服装,每个都有多种颜色选择。每个发型都适合与物理资源一起使用,并包含各种表情和音素混合形状。 下载:Unity资源商店链接资源下载链接 效果图:...
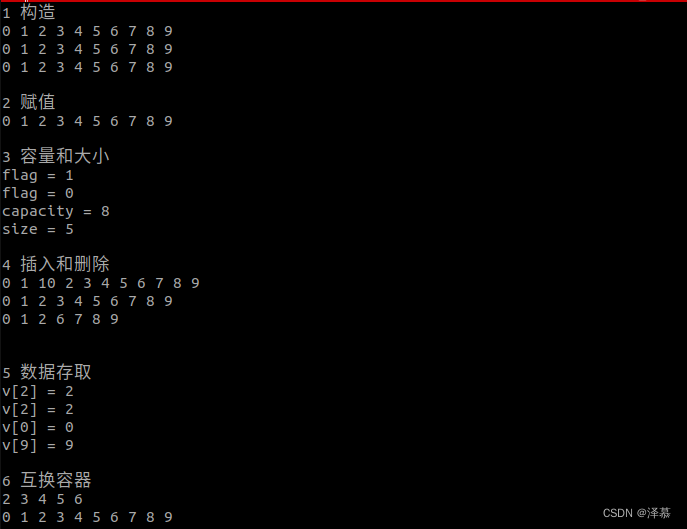
vector容器
以下是关于vector容器的总结 1、构造容器 2、容器赋值 3、获取容量capacity和大小size 4、插入和删除 5、数据存取 6、互换容器和预留空间 #include <iostream> #include <vector>using namespace std; // vector数据结构和数组非常相似,也称为单端数组…...

二进制常用知识整理<java>
1、进制转换: int转二进制: public static void main(String[] args) {int a 0b100;//0b表示后面的为二进制表示,0开始表示八进制System.out.println(a);System.out.println(Integer.toBinaryString(a));System.out.println(Integer.toStr…...

基于Docker的淘客返利平台部署
基于Docker的淘客返利平台部署 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在本文中,我们将探讨如何利用Docker技术来部署一个淘客返利平台。Doc…...
【涵子来信科技潮流】——WWDC24回顾与暑假更新说明
期末大关,即将来袭。在期末之前,我想发一篇文章,介绍有关WWDC24的内容和暑假中更新的说明。本篇文章仅为个人看法和分享,如需了解更多详细内容,请通过官方渠道或者巨佬文章进行进一步了解。 OK, Lets go. 一、WWDC24 …...
)
重温react-08(createContext使用方式)
react中的createContext使用方式 简介一下,就是组件之间可以互相通信的比较好用的传值方式,话不多说直接上代码。 以下介绍的是类组件中的方式,在函数组件中不是如此使用的。 定义一个通用的方法 import { createContext } from "react…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
