力扣第218题“天际线问题”
在本篇文章中,我们将详细解读力扣第218题“天际线问题”。通过学习本篇文章,读者将掌握如何使用扫描线算法和堆来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。
问题描述
力扣第218题“天际线问题”描述如下:
城市的天际线是从远处观看建筑物形成的轮廓。现在,给你所有建筑物的位置和高度,绘制出它们的天际线。
每个建筑物的几何信息用三元组表示
[left, right, height],其中left是建筑物的左边缘,right是建筑物的右边缘,height是建筑物的高度。天际线应该表示为由 “关键点” 组成的列表,其中每个关键点是一个二维坐标(x, y)并按照 x 坐标进行排序。关键点是天际线在 x 轴上图形的转折点。注意,最左侧的建筑物可能会影响天际线的高度,而最右侧建筑物可能会影响天际线的高度。示例:
输入: [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] 输出: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]示例:
输入: [[0,2,3],[2,5,3]] 输出: [[0,3],[5,0]]
解题思路
方法:扫描线算法和最大堆
-
初步分析:
- 使用扫描线算法可以有效地处理建筑物的左右边缘,并维护当前的最大高度。
- 通过最大堆来动态维护当前的最高建筑物高度。
-
步骤:
- 将所有的建筑物边缘按照 x 坐标排序,如果 x 坐标相同,按左边缘先于右边缘排序。
- 使用一个最大堆来维护当前的建筑物高度。
- 遍历所有的边缘,更新堆和结果列表。
代码实现
import heapqdef getSkyline(buildings):events = []for l, r, h in buildings:events.append((l, -h, r))events.append((r, 0, 0))events.sort()result = [[0, 0]]max_heap = [(0, float("inf"))]for x, neg_h, r in events:while max_heap[0][1] <= x:heapq.heappop(max_heap)if neg_h:heapq.heappush(max_heap, (neg_h, r))if result[-1][1] != -max_heap[0][0]:result.append([x, -max_heap[0][0]])return result[1:]# 测试案例
print(getSkyline([[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]])) # 输出: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
print(getSkyline([[0,2,3],[2,5,3]])) # 输出: [[0,3],[5,0]]
复杂度分析
- 时间复杂度:O(n log n),其中 n 是建筑物的数量。排序操作和堆操作的时间复杂度均为 O(n log n)。
- 空间复杂度:O(n),用于存储事件和堆。
模拟面试问答
问题 1:你能描述一下如何解决这个问题的思路吗?
回答:我们可以使用扫描线算法和最大堆来解决这个问题。通过遍历所有的建筑物边缘,维护一个最大堆来动态更新当前的最高建筑物高度,并在每个关键点记录下当前的天际线高度变化。
问题 2:为什么选择使用扫描线算法和最大堆来解决这个问题?
回答:扫描线算法通过遍历所有的建筑物边缘,可以有效地处理建筑物的左右边缘,并维护当前的最大高度。最大堆可以高效地动态维护当前的最高建筑物高度,从而解决天际线问题。
问题 3:你的算法的时间复杂度和空间复杂度是多少?
回答:算法的时间复杂度为 O(n log n),其中 n 是建筑物的数量。排序操作和堆操作的时间复杂度均为 O(n log n)。空间复杂度为 O(n),用于存储事件和堆。
问题 4:在代码中如何处理边界情况?
回答:对于没有建筑物的情况,可以直接返回空列表。通过这种方式,可以处理边界情况。
问题 5:你能解释一下扫描线算法的工作原理吗?
回答:扫描线算法通过遍历所有的建筑物边缘,将其按照 x 坐标排序,并使用最大堆来动态维护当前的最高建筑物高度。在每个关键点记录下当前的天际线高度变化,从而绘制出天际线。
问题 6:在代码中如何确保返回的结果是正确的?
回答:通过遍历所有的建筑物边缘,维护最大堆,并在每个关键点记录下当前的天际线高度变化,确保返回的结果是正确的。可以通过测试案例验证结果。
问题 7:你能举例说明在面试中如何回答优化问题吗?
回答:在面试中,如果面试官问到如何优化算法,我会首先分析当前算法的瓶颈,如时间复杂度和空间复杂度,然后提出优化方案。例如,可以通过减少不必要的操作和优化数据结构来提高性能。解释其原理和优势,最后提供优化后的代码实现。
问题 8:如何验证代码的正确性?
回答:通过运行代码并查看结果,验证返回的天际线是否正确。可以使用多组测试数据,包括正常情况和边界情况,确保代码在各种情况下都能正确运行。例如,可以在测试数据中包含多个不同的建筑物,确保代码结果正确。
问题 9:你能解释一下解决天际线问题的重要性吗?
回答:解决天际线问题在计算几何和图形学中具有重要意义。通过学习和应用扫描线算法和堆,可以提高处理复杂几何问题和动态数据结构的能力。在实际应用中,天际线问题广泛用于城市规划、建筑设计和数据可视化等领域。
问题 10:在处理大数据集时,算法的性能如何?
回答:算法的性能取决于建筑物的数量。在处理大数据集时,通过优化扫描线算法和堆的实现,可以显著提高算法的性能。例如,通过减少不必要的操作和优化堆操作,可以减少时间和空间复杂度,从而提高算法的效率。
总结
本文详细解读了力扣第218题“天际线问题”,通过使用扫描线算法和堆的方法高效地解决了这一问题,并提供了详细的解释和模拟面试问答。希望读者通过本文的学习,能够在力扣刷题的过程中更加得心应手。
相关文章:

力扣第218题“天际线问题”
在本篇文章中,我们将详细解读力扣第218题“天际线问题”。通过学习本篇文章,读者将掌握如何使用扫描线算法和堆来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第…...
帝国cms未审核文章可视化预览效果
有时候为了让编辑更加清楚的看到别人审核之后的效果,同时文章有需要下一级审核才能在前端展示出来,今天就来展示一个未审核文章预览审核后的效果 这次给某出版社开发的时候,他们需要实现编辑能够预览自己发布之后的审核效果,所以就…...
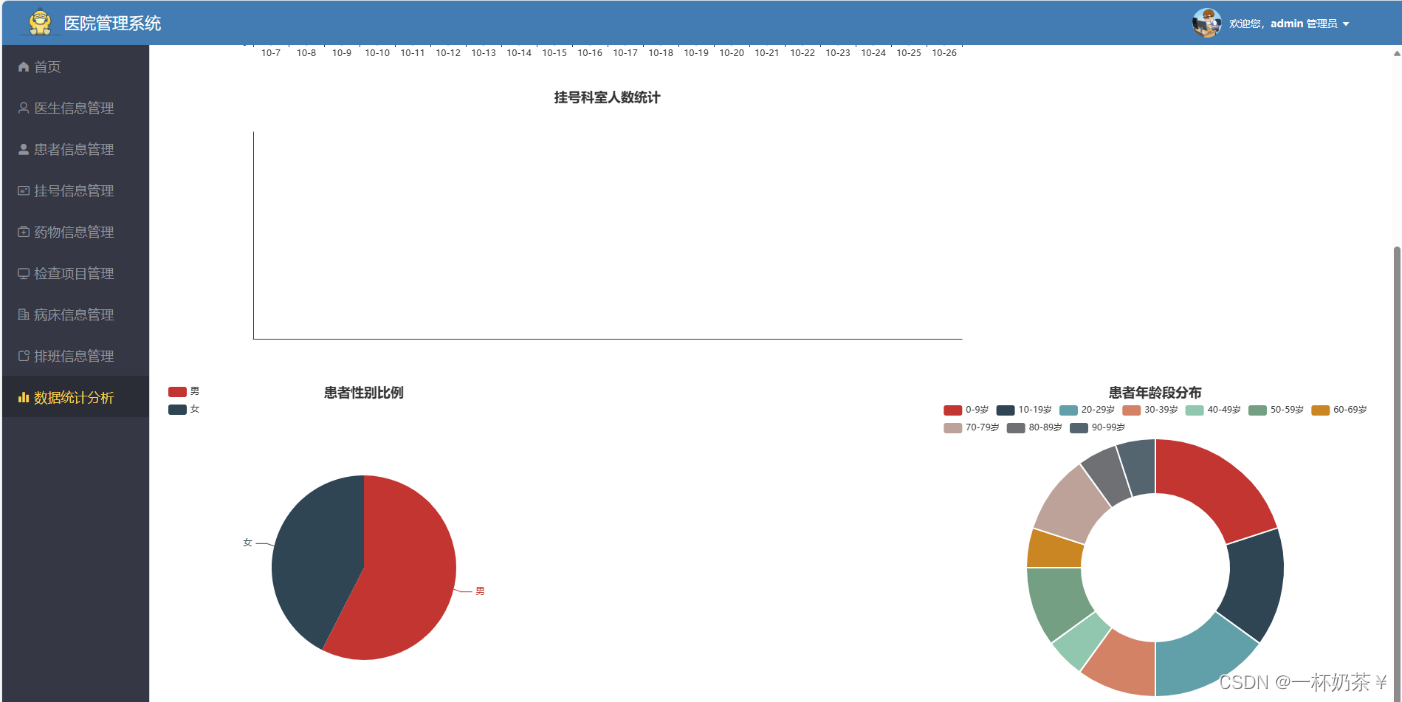
医院管理系统带万字文档医院预约挂号管理系统基于spingboot和vue的前后端分离java项目java课程设计java毕业设计
文章目录 仓库管理系统一、项目演示二、项目介绍三、万字项目文档四、部分功能截图五、部分代码展示六、底部获取项目源码带万字文档(9.9¥带走) 仓库管理系统 一、项目演示 医院管理系统 二、项目介绍 基于springbootvue的前后端分离医院管…...

爬虫技术在物联网数据采集中的应用
爬虫技术在物联网数据采集中的应用案例主要包括以下几个方面: 电商平台数据采集:例如,使用Python编写的网络爬虫可以用于爬取京东网页相关数据,如品牌、标题、价格、店铺等,并进行数据处理及可视化展示。这种方法不仅可…...
spring boot初始化的几个总结
spring intializr File->New->Project 注意:Spring Initializer中 Java版本选择模块已经不支持1.8了。 Spring Boot 3.x要求 Java最低版本为17, 最新的SpringBoot版本已经要求Java22了 所以,你可以升级Java版本,使用Spri…...

springcloud第4季 seata报could not find any implementation for class
一 问题说明 1.1 描述 在使用seata2.0alibaba-cloud 2022.0.0.0-RC2nacos 2.2.3 模拟下订单分布式事务场景,出现如下问题:java.lang.ArrayIndexOutOfBoundsException: Index 0 out of bounds for length 0 查看服务端:java.util.ServiceCo…...

IT之家最新科技热点
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

对象实例化过程
目录 一、Java对象实例化在JVM中的过程: 类加载与初始化 分配内存 初始化对象内存 设置对象头 执行初始化方法 构造方法执行 二、对象的创建过程 一、Java对象实例化在JVM中的过程: 类加载与初始化: 当JVM需要实例化一个对象时,它…...

常见漏洞之XSS
一、XSS简介 XSS(Cross-Site Scripting,跨站脚本攻击)是一种常见的网络攻击方式,通过在网页中注入恶意脚本,当其他用户浏览这些网页时,这些嵌入的恶意脚本会在其浏览器上执行,从而进行各种恶意…...
Python变量的命名规则与赋值方式
第二章:Python 基础语法 第一节:变量的命名规则与赋值方式 2.1.1 引言 在编程中,变量是存储数据的基本单元。变量的命名和赋值是编程语言中表达和操作数据的基础。了解和遵循变量命名规则对于编写清晰、可维护的代码至关重要。 2.1.2 变量…...

昇思25天学习打卡营第7天|网络构建
昇思25天学习打卡营第7天|网络构建 前言函数式自动微分函数与计算图微分函数与梯度计算Stop GradientAuxiliary data神经网络梯度计算 个人任务打卡(读者请忽略)个人理解与总结 前言 非常感谢华为昇思大模型平台和CSDN邀请体验昇思大模型!从今…...
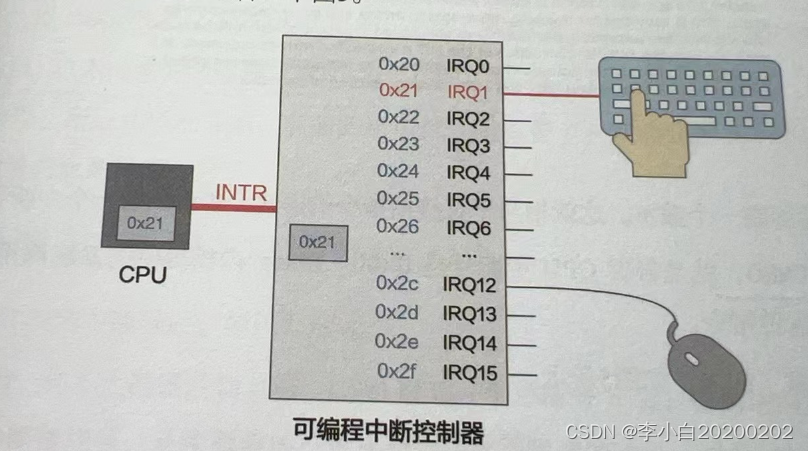
扩展阅读:什么是中断
如果用一句话概括操作系统的原理,那就是:整个操作系统就是一个中断驱动的死循环,用最简单的代码解释如下: while(true){doNothing(); } 其他所有事情都是由操作系统提前注册的中断机制和其对应的中断处理函数完成的。我们点击一下鼠标,敲击一下键盘,执行一个程序,…...

git 命令学习之branch 和 tag 操作
引言 在项目一个迭代过程结束之时,或是一个版本发布之后,我们要进行 新版本的开发,这时就需要对原来的项目代码进行封存,以及新项目代码的开始,这时就需要用到 branch 和 tag 操作。下面简单说说对这两个操作的理解。…...

如何理解 IEEE 754 单精度浮点型能表示的最小绝对值、最大绝对值
文章目录 解答最小绝对值最大绝对值总结 细节理解1. 为什么非规格化数的指数偏移量为126(而不是127)?规格化数与非规格化数非规格化数的指数偏移量非规格化数的尾数非规格化数的值示例 解答 IEEE 754单精度浮点数使用32位来表示一个数值&…...
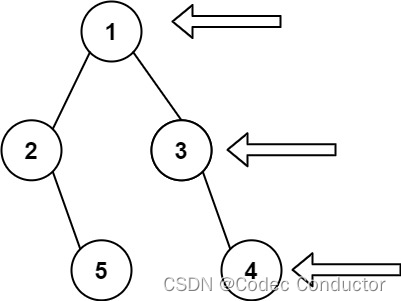
LeetCode 算法:二叉树的右视图 c++
原题链接🔗:二叉树的右视图 难度:中等⭐️⭐️ 题目 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 示例 1: 输入: [1,2,3,null,5,null,4…...

Java 并发编程常见问题
1、线程状态它们之间是如何扭转的? 1、谈谈对于多线程的理解? 1、对于多核CPU,多线程可以提升CPU的利用率; 2、对于多IO操作的程序,多线程可以提升系统的整体性能及吞吐量; 3、使用多线程在一些场景下可…...

网络基础:静态路由
静态路由是一种由网络管理员手动配置的路由方式,用于在网络设备(如路由器或交换机)之间传递数据包。与动态路由不同,静态路由不会根据网络状态的变化自动调整。 不同厂商的网络设备在静态路由的配置上有些许差异;下面…...
库存管理系统基于spingboot vue的前后端分离仓库库存管理系统java项目java课程设计java毕业设计
文章目录 库存管理系统一、项目演示二、项目介绍三、部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 库存管理系统 一、项目演示 库存管理系统 二、项目介绍 基于spingboot和vue前后端分离的库存管理系统 功能模块ÿ…...
【ArcGIS AddIn插件】【可用于全国水旱灾害风险普查】全网最强洪水淹没分析插件-基于8邻域种子搜索算法-有源淹没分析算法
最近有很多GIS小伙伴咨询我关于基于8邻域种子搜索算法的有源淹没分析插件的使用方法及原理,咱们通过这篇文章给大家详细介绍下这款插件的运行机制。 一、插件类型及适用版本 本插件属于ArcGIS AddIn工具条插件,基于ArcGIS Engine10.2.2的开发环境开发的&…...
==和equals的区别(面试题)
和equals有什么区别 对于基本数据类型,比较的是值是否相等,对于引用类型则是比较的地址是否相等;对于equals来说,基本数据类型没有equals方法,对于引用类型equals比较的是引用对象是否相同 那针对以上结论,…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
