PINN解偏微分方程实例1
PINN解偏微分方程实例1
- 1. PINN简介
- 2. 偏微分方程实例
- 3. 基于pytorch实现代码
- 4. 数值解
- 参考资料
1. PINN简介
PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。
∂u∂t+u∂u∂x=v∂2u∂x2\begin{align} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=v\frac{\partial^2 u}{\partial x^2} \end{align} ∂t∂u+u∂x∂u=v∂x2∂2u
神经网络输入位置x,y,z和时间t的值,预测偏微分方程解u在这个时空条件下的数值解。
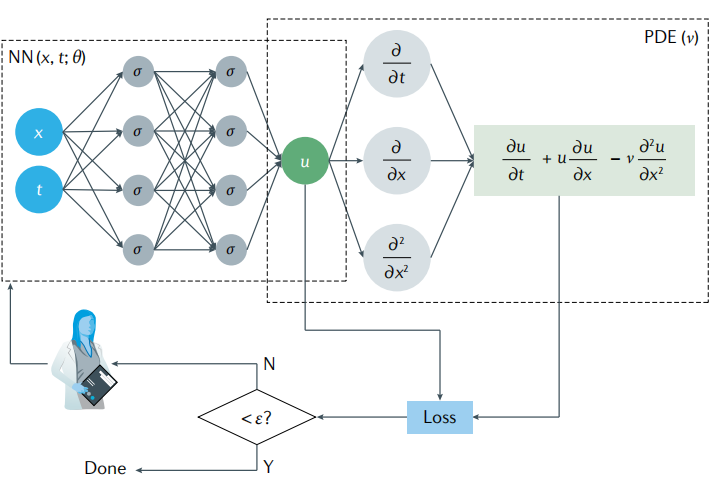
上图中可以看出,PINN的损失函数包含两部分内容,一部分是来源于训练数据误差,另一部分来源于偏微分方程误差,可以记作(2)式。
l=wdataldata+wPDElPDE\begin{align} \mathcal{l} = w_{data}\mathcal{l}_{data}+w_{PDE}\mathcal{l}_{PDE} \end{align} l=wdataldata+wPDElPDE
其中
ldata=1Ndata∑i=1Ndata(u(xi,ti)−ui)2lPDE=1Ndata∑j=1NPDE(∂u∂t+u∂u∂x−v∂2u∂x2)2∣(xj,tj)\begin{align} \begin{aligned} \mathcal{l}_{data} &= \frac{1}{N_{data}}\sum_{i=1}^{N_{data}} (u(x_i,t_i)-u_i)^2 \\ \mathcal{l}_{PDE} &= \frac{1}{N_{data}}\sum_{j=1}^{N_{PDE}} \left( \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}-v\frac{\partial^2 u}{\partial x^2} \right)^2|_{(x_j,t_j)} \end{aligned} \end{align} ldatalPDE=Ndata1i=1∑Ndata(u(xi,ti)−ui)2=Ndata1j=1∑NPDE(∂t∂u+u∂x∂u−v∂x2∂2u)2∣(xj,tj)
2. 偏微分方程实例
考虑偏微分方程如下:
∂2u∂x2−∂4u∂y4=(2−x2)e−y\begin{align} \begin{aligned} \frac{\partial^2 u}{\partial x^2} - \frac{\partial^4 u}{\partial y^4} = (2-x^2)e^{-y} \end{aligned} \end{align} ∂x2∂2u−∂y4∂4u=(2−x2)e−y
考虑以下边界条件,
uyy(x,0)=x2uyy(x,1)=x2eu(x,0)=x2u(x,1)=x2eu(0,y)=0u(1,y)=e−y\begin{align} \begin{aligned} u_{yy}(x,0) &= x^2 \\ u_{yy}(x,1) &= \frac{x^2}{e} \\ u(x,0) &= x^2 \\ u(x,1) &= \frac{x^2}{e} \\ u(0,y) &= 0 \\ u(1,y) &= e^{-y} \\ \end{aligned} \end{align} uyy(x,0)uyy(x,1)u(x,0)u(x,1)u(0,y)u(1,y)=x2=ex2=x2=ex2=0=e−y
以上偏微分方程真解为u(x,y)=x2e−yu(x,y)=x^2 e^{-y}u(x,y)=x2e−y,在区域[0,1]×[0,1][0,1]\times[0,1][0,1]×[0,1]上随机采样配置点和数据点,其中配置点用来构造PDE损失函数l1,l2,⋯,l7\mathcal{l}_1,\mathcal{l}_2,\cdots,\mathcal{l}_7l1,l2,⋯,l7,数据点用来构造数据损失函数l8\mathcal{l}_8l8.
l1=1N1∑(xi,yi)∈Ω(u^xx(xi,yi;θ)−u^yyyy(xi,yi;θ)−(2−xi2)e−yi)2l2=1N2∑(xi,yi)∈[0,1]×{0}(u^yy(xi,yi;θ)−xi2)2l3=1N3∑(xi,yi)∈[0,1]×{1}(u^yy(xi,yi;θ)−xi2e)2l4=1N4∑(xi,yi)∈[0,1]×{0}(u^(xi,yi;θ)−xi2)2l5=1N5∑(xi,yi)∈[0,1]×{1}(u^(xi,yi;θ)−xi2e)2l6=1N6∑(xi,yi)∈{0}×[0,1](u^(xi,yi;θ)−0)2l7=1N7∑(xi,yi)∈{1}×[0,1](u^(xi,yi;θ)−e−yi)2l8=1N8∑i=1N8(u^(xi,yi;θ)−ui)2\begin{align} \begin{aligned} \mathcal{l}_1 &= \frac{1}{N_1}\sum_{(x_i,y_i)\in\Omega} (\hat{u}_{xx}(x_i,y_i;\theta) - \hat{u}_{yyyy}(x_i,y_i;\theta) - (2-x_i^2)e^{-y_i})^2 \\ \mathcal{l}_2 &= \frac{1}{N_2}\sum_{(x_i,y_i)\in[0,1]\times\{0\}} (\hat{u}_{yy}(x_i,y_i;\theta) - x_i^2)^2 \\ \mathcal{l}_3 &= \frac{1}{N_3}\sum_{(x_i,y_i)\in[0,1]\times\{1\}} (\hat{u}_{yy}(x_i,y_i;\theta) - \frac{x_i^2}{e})^2 \\ \mathcal{l}_4 &= \frac{1}{N_4}\sum_{(x_i,y_i)\in[0,1]\times\{0\}} (\hat{u}(x_i,y_i;\theta) - x_i^2)^2 \\ \mathcal{l}_5 &= \frac{1}{N_5}\sum_{(x_i,y_i)\in[0,1]\times\{1\}} (\hat{u}(x_i,y_i;\theta) - \frac{x_i^2}{e})^2 \\ \mathcal{l}_6 &= \frac{1}{N_6}\sum_{(x_i,y_i)\in\{0\}\times [0,1]}(\hat{u}(x_i,y_i;\theta) - 0)^2 \\ \mathcal{l}_7 &= \frac{1}{N_7}\sum_{(x_i,y_i)\in\{1\}\times [0,1]}(\hat{u}(x_i,y_i;\theta) - e^{-y_i})^2 \\ \mathcal{l}_8 &= \frac{1}{N_{8}}\sum_{i=1}^{N_{8}} (\hat{u}(x_i,y_i;\theta)-u_i)^2 \end{aligned} \end{align} l1l2l3l4l5l6l7l8=N11(xi,yi)∈Ω∑(u^xx(xi,yi;θ)−u^yyyy(xi,yi;θ)−(2−xi2)e−yi)2=N21(xi,yi)∈[0,1]×{0}∑(u^yy(xi,yi;θ)−xi2)2=N31(xi,yi)∈[0,1]×{1}∑(u^yy(xi,yi;θ)−exi2)2=N41(xi,yi)∈[0,1]×{0}∑(u^(xi,yi;θ)−xi2)2=N51(xi,yi)∈[0,1]×{1}∑(u^(xi,yi;θ)−exi2)2=N61(xi,yi)∈{0}×[0,1]∑(u^(xi,yi;θ)−0)2=N71(xi,yi)∈{1}×[0,1]∑(u^(xi,yi;θ)−e−yi)2=N81i=1∑N8(u^(xi,yi;θ)−ui)2
3. 基于pytorch实现代码
"""
A scratch for PINN solving the following PDE
u_xx-u_yyyy=(2-x^2)*exp(-y)
Author: suntao
Date: 2023/2/26
"""
import torch
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Depochs = 10000 # 训练代数
h = 100 # 画图网格密度
N = 1000 # 内点配置点数
N1 = 100 # 边界点配置点数
N2 = 1000 # PDE数据点def setup_seed(seed):torch.manual_seed(seed)torch.cuda.manual_seed_all(seed)torch.backends.cudnn.deterministic = True# 设置随机数种子
setup_seed(888888)# Domain and Sampling
def interior(n=N):# 内点x = torch.rand(n, 1)y = torch.rand(n, 1)cond = (2 - x ** 2) * torch.exp(-y)return x.requires_grad_(True), y.requires_grad_(True), conddef down_yy(n=N1):# 边界 u_yy(x,0)=x^2x = torch.rand(n, 1)y = torch.zeros_like(x)cond = x ** 2return x.requires_grad_(True), y.requires_grad_(True), conddef up_yy(n=N1):# 边界 u_yy(x,1)=x^2/ex = torch.rand(n, 1)y = torch.ones_like(x)cond = x ** 2 / torch.ereturn x.requires_grad_(True), y.requires_grad_(True), conddef down(n=N1):# 边界 u(x,0)=x^2x = torch.rand(n, 1)y = torch.zeros_like(x)cond = x ** 2return x.requires_grad_(True), y.requires_grad_(True), conddef up(n=N1):# 边界 u(x,1)=x^2/ex = torch.rand(n, 1)y = torch.ones_like(x)cond = x ** 2 / torch.ereturn x.requires_grad_(True), y.requires_grad_(True), conddef left(n=N1):# 边界 u(0,y)=0y = torch.rand(n, 1)x = torch.zeros_like(y)cond = torch.zeros_like(x)return x.requires_grad_(True), y.requires_grad_(True), conddef right(n=N1):# 边界 u(1,y)=e^(-y)y = torch.rand(n, 1)x = torch.ones_like(y)cond = torch.exp(-y)return x.requires_grad_(True), y.requires_grad_(True), conddef data_interior(n=N2):# 内点x = torch.rand(n, 1)y = torch.rand(n, 1)cond = (x ** 2) * torch.exp(-y)return x.requires_grad_(True), y.requires_grad_(True), cond# Neural Network
class MLP(torch.nn.Module):def __init__(self):super(MLP, self).__init__()self.net = torch.nn.Sequential(torch.nn.Linear(2, 32),torch.nn.Tanh(),torch.nn.Linear(32, 32),torch.nn.Tanh(),torch.nn.Linear(32, 32),torch.nn.Tanh(),torch.nn.Linear(32, 32),torch.nn.Tanh(),torch.nn.Linear(32, 1))def forward(self, x):return self.net(x)# Loss
loss = torch.nn.MSELoss()def gradients(u, x, order=1):if order == 1:return torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),create_graph=True,only_inputs=True, )[0]else:return gradients(gradients(u, x), x, order=order - 1)# 以下7个损失是PDE损失
def l_interior(u):# 损失函数L1x, y, cond = interior()uxy = u(torch.cat([x, y], dim=1))return loss(gradients(uxy, x, 2) - gradients(uxy, y, 4), cond)def l_down_yy(u):# 损失函数L2x, y, cond = down_yy()uxy = u(torch.cat([x, y], dim=1))return loss(gradients(uxy, y, 2), cond)def l_up_yy(u):# 损失函数L3x, y, cond = up_yy()uxy = u(torch.cat([x, y], dim=1))return loss(gradients(uxy, y, 2), cond)def l_down(u):# 损失函数L4x, y, cond = down()uxy = u(torch.cat([x, y], dim=1))return loss(uxy, cond)def l_up(u):# 损失函数L5x, y, cond = up()uxy = u(torch.cat([x, y], dim=1))return loss(uxy, cond)def l_left(u):# 损失函数L6x, y, cond = left()uxy = u(torch.cat([x, y], dim=1))return loss(uxy, cond)def l_right(u):# 损失函数L7x, y, cond = right()uxy = u(torch.cat([x, y], dim=1))return loss(uxy, cond)# 构造数据损失
def l_data(u):# 损失函数L8x, y, cond = data_interior()uxy = u(torch.cat([x, y], dim=1))return loss(uxy, cond)# Trainingu = MLP()
opt = torch.optim.Adam(params=u.parameters())for i in range(epochs):opt.zero_grad()l = l_interior(u) \+ l_up_yy(u) \+ l_down_yy(u) \+ l_up(u) \+ l_down(u) \+ l_left(u) \+ l_right(u) \+ l_data(u)l.backward()opt.step()if i % 100 == 0:print(i)# Inference
xc = torch.linspace(0, 1, h)
xm, ym = torch.meshgrid(xc, xc)
xx = xm.reshape(-1, 1)
yy = ym.reshape(-1, 1)
xy = torch.cat([xx, yy], dim=1)
u_pred = u(xy)
u_real = xx * xx * torch.exp(-yy)
u_error = torch.abs(u_pred-u_real)
u_pred_fig = u_pred.reshape(h,h)
u_real_fig = u_real.reshape(h,h)
u_error_fig = u_error.reshape(h,h)
print("Max abs error is: ", float(torch.max(torch.abs(u_pred - xx * xx * torch.exp(-yy)))))
# 仅有PDE损失 Max abs error: 0.004852950572967529
# 带有数据点损失 Max abs error: 0.0018916130065917969# 作PINN数值解图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_pred_fig.detach().numpy())
ax.text2D(0.5, 0.9, "PINN", transform=ax.transAxes)
plt.show()
fig.savefig("PINN solve.png")# 作真解图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_real_fig.detach().numpy())
ax.text2D(0.5, 0.9, "real solve", transform=ax.transAxes)
plt.show()
fig.savefig("real solve.png")# 误差图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_error_fig.detach().numpy())
ax.text2D(0.5, 0.9, "abs error", transform=ax.transAxes)
plt.show()
fig.savefig("abs error.png")
4. 数值解
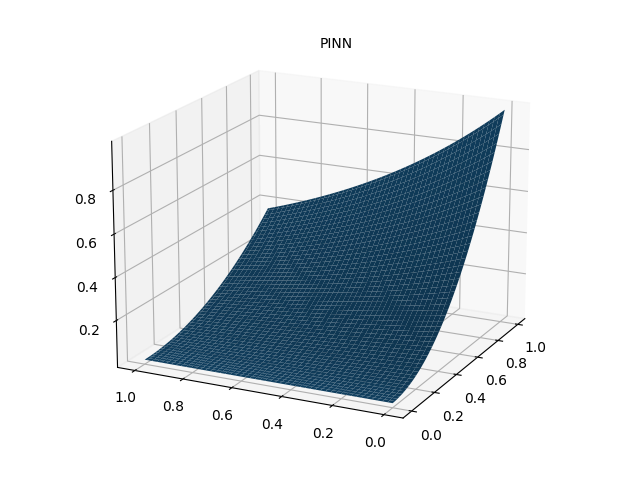
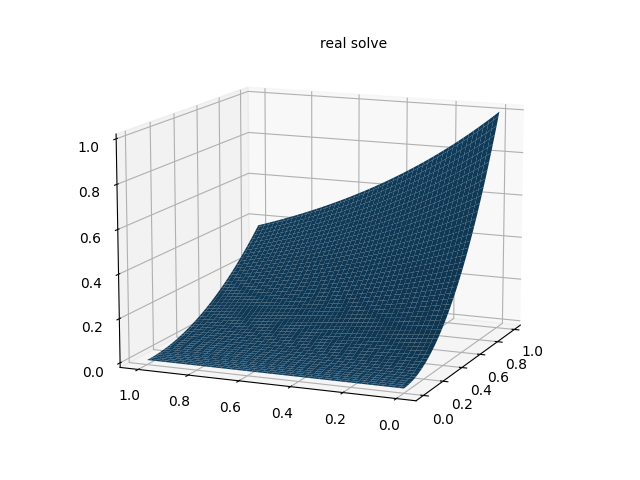
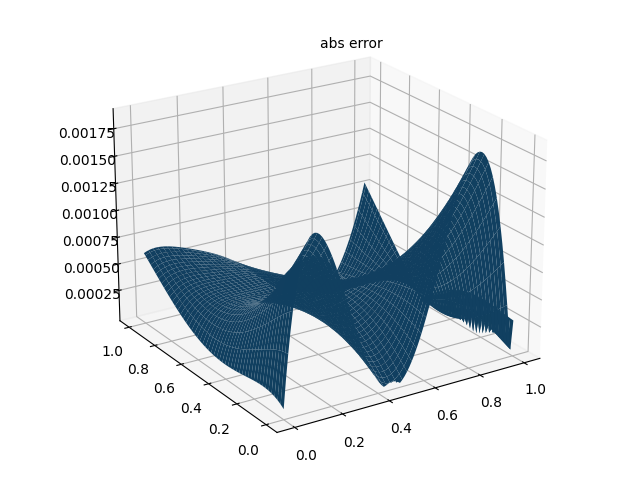
参考资料
[1]. Physics-informed machine learning
[2]. 知乎-PaperWeekly
相关文章:

PINN解偏微分方程实例1
PINN解偏微分方程实例11. PINN简介2. 偏微分方程实例3. 基于pytorch实现代码4. 数值解参考资料1. PINN简介 PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。 ∂u∂tu∂u∂xv∂2u∂x2\begin{align} \frac{…...

【python 基础篇 十二】python的函数-------函数生成器
目录1.生成器基本概念2.生成器的创建方式3.生成器的输出方式4.send()方法5.关闭生成器6.注意事项1.生成器基本概念 是一个特色的迭代器(迭代器的抽象层级更高)所以拥有迭代器的特性 惰性计算数据 节省内存 ----就是不是立马生成所有数据,而是…...
elasticsearch全解 (待续)
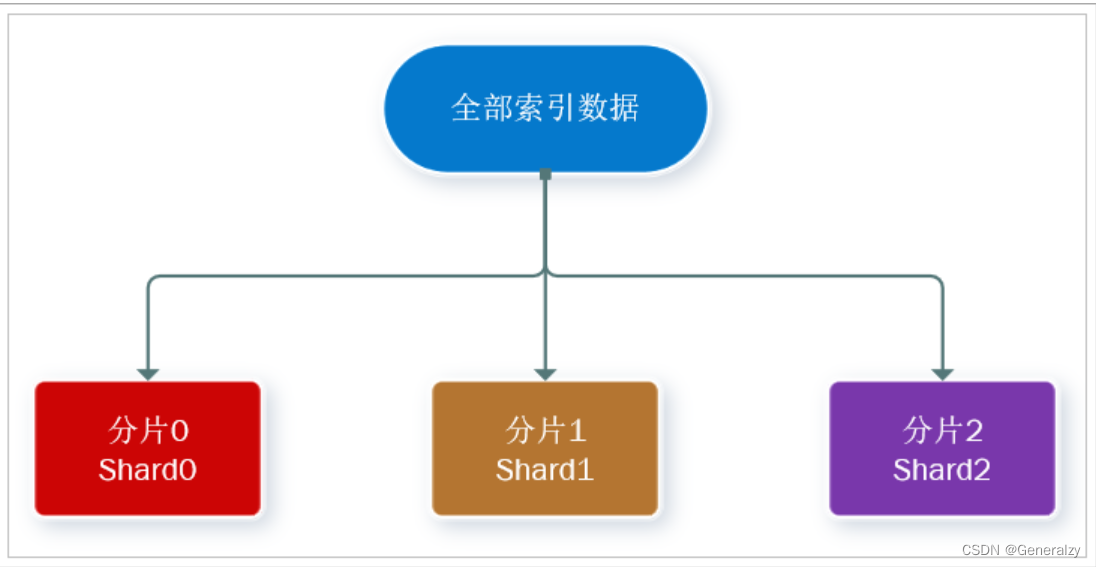
目录elasticsearchELK技术栈Lucene与Elasticsearch关系为什么不是其他搜索技术?Elasticsearch核心概念Cluster:集群Node:节点Shard:分片Replia:副本全文检索倒排索引正向和倒排es的一些概念文档和字段索引和映射mysql与…...

springboot2集成knife4j
springboot2集成knife4j springboot2集成knife4j 环境说明集成knife4j 第一步:引入依赖第二步:编写配置类第三步:测试一下 第一小步:编写controller第二小步:启动项目,访问api文档 相关资料 环境说明 …...

Qt 性能优化:CPU占有率高的现象和解决办法
一、前言 在最近的项目中,发现执行 Qt 程序时,有些情况下的 CPU 占用率奇高,最高高达 100%。项目跑在嵌入式板子上,最开始使用 EGLFS 插件,但是由于板子没有单独的鼠标层,导致鼠标移动起来卡顿,…...

MySQL专题(学会就毕业)
MySQL专题0.准备sql设计一张员工信息表,要求如下:编号(纯数字)员工工号 (字符串类型,长度不超过10位)员工姓名(字符串类型,长度不超过10位)性别(男/女,存储一…...

Java高级技术:单元测试、反射、注解
目录 单元测试 单元测试概述 单元测试快速入门 单元测试常用注解 反射 反射概述 反射获取类对象 反射获取构造器对象 反射获取成员变量对象 反射获取方法对象 反射的作用-绕过编译阶段为集合添加数据 反射的作用-通用框架的底层原理 注解 注解概述 自定义注解 …...

C语言初识
#include <stdio.h>//这种写法是过时的写法 void main() {}//int是整型的意思 //main前面的int表示main函数调用后返回一个整型值 int main() {return 0; }int main() { //主函数--程序的入口--main函数有且仅有一个//在这里完成任务//在屏幕伤输出hello world//函数-pri…...

Cadence Allegro 导出Etch Length by Layer Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Etch Length by Layer Report作用3,Etch Length by Layer Report示例4,Etch Length by Layer Report导出方法4.2,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
无监督对比学习(CL)最新必读经典论文整理分享
对比自监督学习技术是一种很有前途的方法,它通过学习对使两种事物相似或不同的东西进行编码来构建表示。Contrastive learning有很多文章介绍,区别于生成式的自监督方法,如AutoEncoder通过重建输入信号获取中间表示,Contrastive M…...

最长回文子串【Java实现】
题目描述 现有一个字符串s,求s的最长回文子串的长度 输入描述 一个字符串s,仅由小写字母组成,长度不超过100 输出描述 输出一个整数,表示最长回文子串的长度 样例 输入 lozjujzve输出 // 最长公共子串为zjujz,长度为…...

LeetCode 438. Find All Anagrams in a String
LeetCode 438. Find All Anagrams in a String 题目描述 Given two strings s and p, return an array of all the start indices of p’s anagrams in s. You may return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a…...
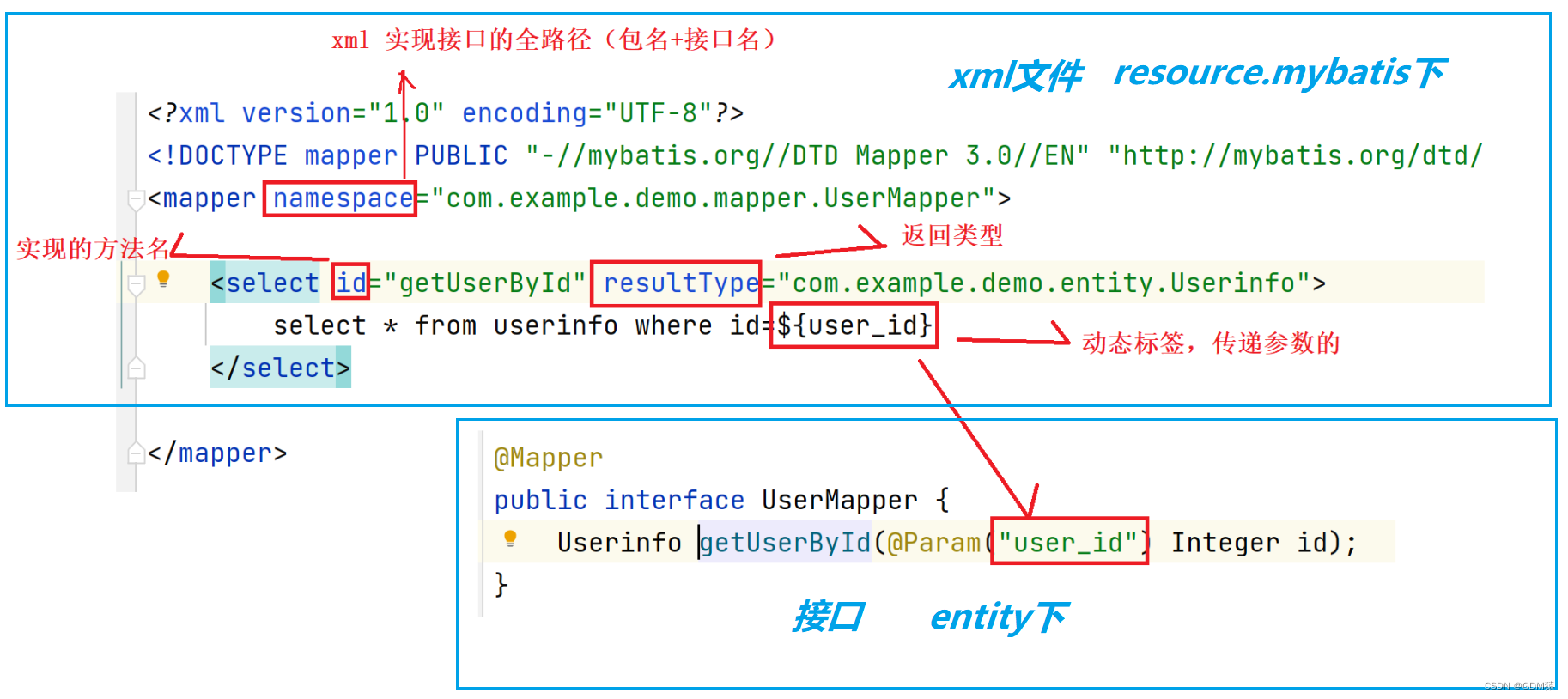
MyBatis-1:基础概念+环境配置
什么是MyBatis?MyBatis是一款优秀的持久层框架,支持自定义sql,存储过程以及高级映射。MyBatis就是可以让我们更加简单的实现程序和数据库之间进行交互的一个工具。可以让我们更加简单的操作和读取数据库的内容。MyBatis的官网:htt…...

R语言基础(五):流程控制语句
R语言基础(一):注释、变量 R语言基础(二):常用函数 R语言基础(三):运算 R语言基础(四):数据类型 6.流程控制语句 和大多数编程语言一样,R语言支持选择结构和循环结构。 6.1 选择语句 选择语句是当条件满足的时候才执行…...

【Java开发】设计模式 02:工厂模式
1 工厂模式介绍工厂模式(Factory Pattern)是 Java 中最常用的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使…...
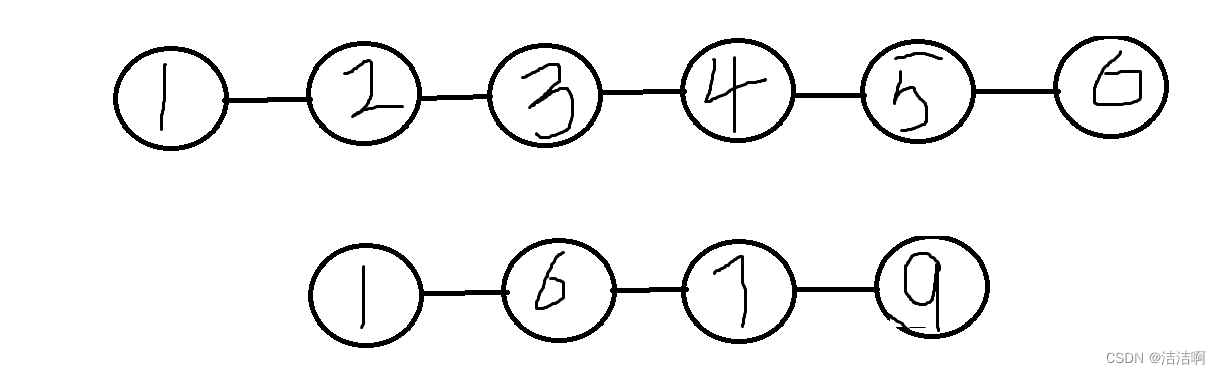
合并两个链表(自定义位置合并与有序合并)LeetCode--OJ题详解
图片: csdn 自定义位置合并 问题: 给两个链表 list1 和 list2 ,它们包含的元素分别为 n 个和 m 个。 请你将 list1 中 下标从 a 到 b 的全部节点都删除,并将list2 接在被删除节点 的位置。 比如: 输入:list1 [1…...

Java编程问题总结
Java编程问题总结 整理自 https://github.com/giantray/stackoverflow-java-top-qa 基础语法 将InputStream转换为String apache commons-io String content IOUtils.toString(new FileInputStream(file), StandardCharsets.UTF_8); //String value FileUtils.readFileT…...

binutils工具集——objcopy的用法
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 一、工具简介 objcopy主要用来转换目标文件的格式。 在实际开发中,我们会用该工具进行格式转换与内容删除。 (1)在链接完成后,将elf格式的.out文件转化为bi…...
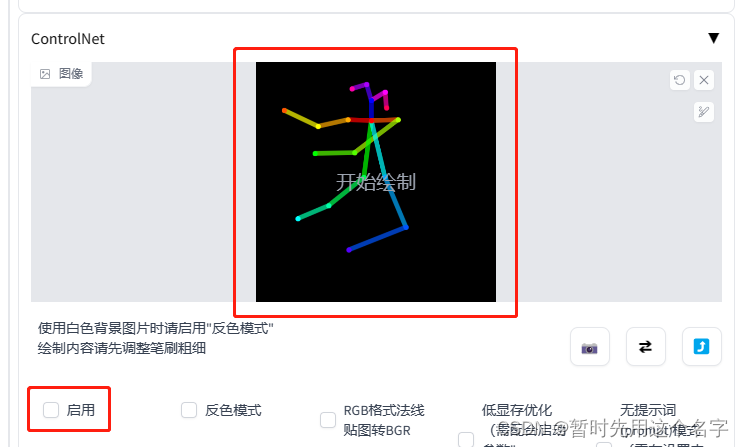
Windows使用Stable Diffusion时遇到的各种问题和知识点整理(更新中...)
Stable Diffusion安装完成后,在使用过程中会出现卡死、文件不存在等问题,在本文中将把遇到的问题陆续记录下来,有兴趣的朋友可以参考。 如果要了解如何安装sd,则参考本文《Windows安装Stable Diffusion WebUI及问题解决记录》。如…...
MySQL workbench基本查询语句
1.查询所有字段所有记录 SELECT * FROM world.city; select 表示查询;“*” 称为通配符,也称为“标配符”。表示将表中所有的字段都查询出来;from 表示从哪里查询;world.city 表示名为world的数据库中的city表; 上面…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
