MDPs —— 马尔可夫决策定义与算法
文章目录
- MDPs 定义——由实例开始
- 时序决策问题
- 给游戏增点乐子
- *为什么要有折扣
- 游戏的解——原则
- 所以,什么是 MDPs?
- MDPs 的基本原理、表示
- 光环原理
- 效用的求解是反向传播的
- 原则不变条件
- MDPs 的表示
- MDPs 求解
- 效用迭代法
- 缺点
- 原则迭代法
MDPs 定义——由实例开始
时序决策问题
假设有一个 agent,从下图的 start 开始,移动到图中的 +1、-1 两个状态时,游戏结束。其中阴影部分是 agent 的无法移动区域,图如下:
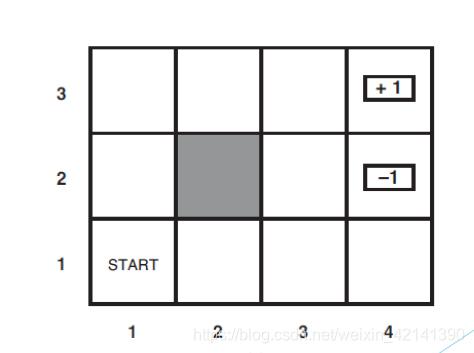
在这个游戏中,很明显可以用几个状态表示,首先是 agent 目前所在的状态(位置)集合,S = {s1,s2,…,sn},以及可以采取的动作集 A(s)。在此游戏中,很明显 A(s) = { 上下左右 }。
对于马尔可夫过程而言, A(s) 是不可靠的。具体地说,假设当前的 agent 采用了 “上”,那么在现实的实现中,有 80% 的概率走上,10% 的概率走右,10% 走左。因此,假如 agent 目前处于状态(位置) s,那么下一个动作后,agent 来到 s’ 需要用一个新的变量——状态转移模型 来表示,记为 P(s’|s,a);
可以看到,这个游戏的下一个状态,取决于上一个状态。而且这几个格子里面是什么情况,这几个格子的布局是什么,终点在哪里,都是已知的。这个游戏,其实也是一个时序决策过程。也就是说,环境已知,状态是通过上一个状态,转移到下一个状态。
给游戏增点乐子
当然,如果这个游戏只是单纯地走到 +1、-1,然后游戏结束,未免太过无聊。为了给游戏增加乐趣,我们给每一个格子都加入一个附加回报。所以 agent 在进行状态转移时(从一个格子,到另一个格子),都会积累一个回报,记为 R(s’,a,s)。当然,这个 R(s’,a,s) 可正可负,并且具有上下界。
然后,我们修改一下游戏获胜规则。为此定义一个效用函数,其定义为:agent 从当前状态(不是初始状态)到目标状态所经历的轨迹中,所有 回报之和。
当然,效用有两种计算方式,如下:
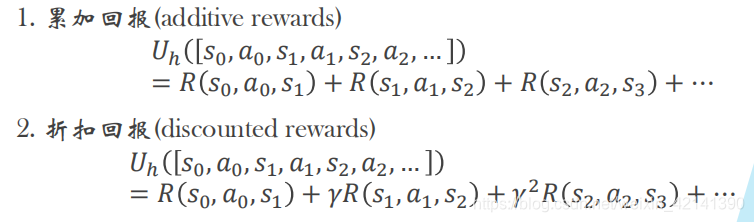
*为什么要有折扣
如果 agent 可以走无限多步,且 R 有正数,那么可以无限地来回走动,来实现效用无穷大,这样就没有意思了。采用折扣累加,就不会出现无穷大的情况,证明如下:

举个例子,加入上图除了+1/-1 格子外,所有格子的回报都是 -0.04。如果 agent 走了 10 步到了 +1,那么 start 的效用就是:-0.04x9 +1 = 0.64。
那么,如果是你玩这个游戏,你会采用哪种动作(从 start 开始),从而使得:从初始状态开始,到目标状态所经历的轨迹中,所有回报之和最高。
这个游戏显然由于状态转移的概率性,所以具有一定的随机性。也就是说,没有一种万金油的动作套路,使得积累回报最高。
游戏的解——原则
那么,加入给一个机器人来解决上面的游戏,我们需要给出所有格子,可以采用的最优动作。何谓最优?由于有了概率的参与,最优很显然变成期望最大。什么期望最大呢?当然是所有行动轨迹的效用的期望。
由于状态转移是随机的,因此,我们可以列出的解,就是每一个当 agent 由任意的 s 拉倒 任意的 s’ 时,应该采取的动作组成的集合,我们称这个集合为原则。很显然,原则是一个大小为 |S|^2 的集合,我们记为 π。当 agent 采取某个原则 π 时,显然状态 s 有的期望效用为:

因此,如果要解这个游戏,我们就要找到最优原则:

如果步长无限的情况下,很显然最优原则与初始状态是独立的。
所以,什么是 MDPs?
MDPs 是由以下部分组成的:
- agent 的状态集合 S
- 动作集合 A(s)
- 状态转移概率 P(s’|s,a)
- 效用函数 U(s)
要求的是一个动作原则,使得轨迹中回报的折扣累计的期望最大(效用期望最大)
MDPs 的基本原理、表示
光环原理
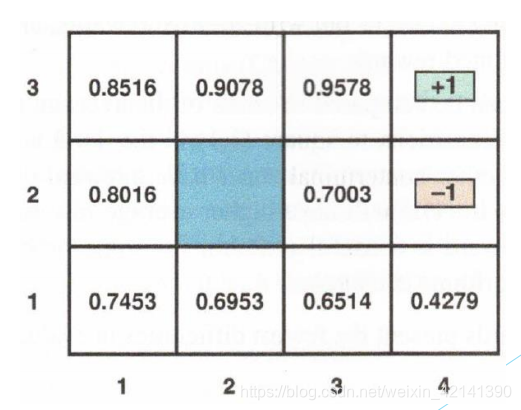
下图给出了每个格子的效用(效用将从后面的算法中求出),很明显,离 +1 越近,则效用越大。因为他走到 +1 所需要的步数最小。注意,MDPs 不会直接给出效用。
效用的求解是反向传播的
假如 agent 的目前状态是 s ,那么最佳原则应该采取的动作 a 应满足:

其中 s’ 为采用 a 后转移的状态,U(s’) 可由下述公式求出,即后续状态序列的折扣累计效用的期望:

此时, 状态 s 的效用是:

这个公式也叫 bellman 公式。
举个例子:
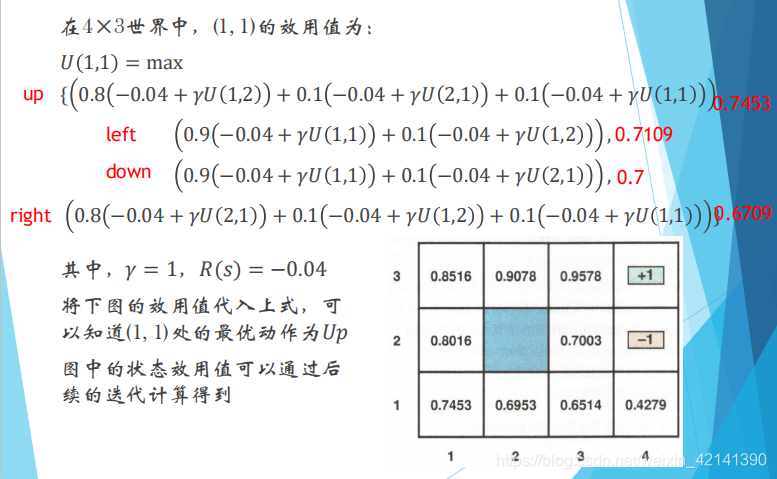
由此也可以看出,一个状态的效用,要从下一个状态的效用求出。而效用的求解,是回报沿着轨迹的累加。因此,效用的求解是反向传播的。
原则不变条件
假如回报 R(s) 进行了线性变化,如 R(s) = aR(s)+b (a>0),那么原则不变。
更进一步的,如果 R’(s’,a,s) = R(s’,a,s) + γ f(s’) - f(s) ,f(s) 是 s 的函数,那么原则也不变。
MDPs 的表示
- 用一个三维表列举所有状态,以及采取动作后来到的下一个状态的效用来表示。显然这个三维表的大小是 S by S by A。
- 用一个动态贝叶斯网络,创建一个动态决策网络,来表示 MDP;这里不详细解释。
MDPs 求解
效用迭代法
从上面的所有内容中,我们大致可以看出,要求解一个最好的 原则 π,必须先求出所有格子、在最优动作下的效用。我们可以用 bellman 公式来求取动作 + 效用:

假如 s 的取值有 n 个,U(s’) 、U(s) 为未知数,那么上式就可以得出 n 个方程组,这个方程组里有 n 个未知数。很显然,联立以上方程,就可以求出方程的解,即所有的 U(s)。
由于这个方程是一个非线性方程(带有 max),所以不能够直接求取。一个求解的方法是数值迭代法,具体如下:

R(s) 也就是 R(s’,a,s),通常是已知的。
用这个算法可以求解出 U(s):
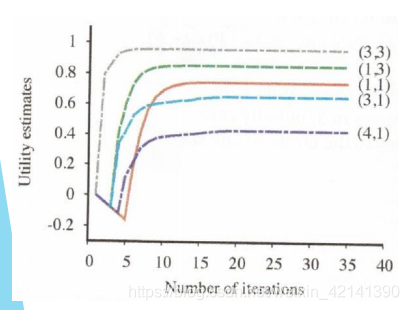
缺点
经过测试,当 δ 还很大的时候,求出来的 原则 π 就已经是最优原则了。由此推出另一个算法,原则迭代算法。
原则迭代法
首先取一个初始原则 π0,求出每一个状态的效用 U(s):

之后:

如是迭代,直到原则不变即可。具体算法如下:

相关文章:

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
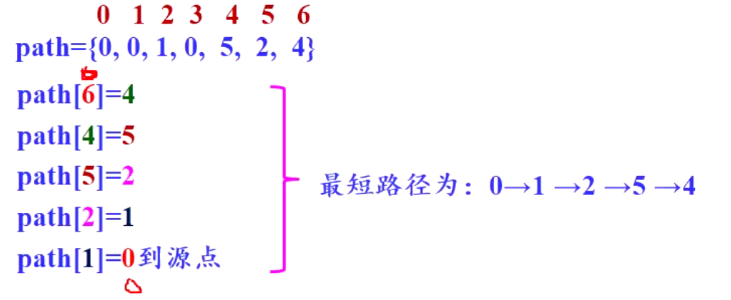
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
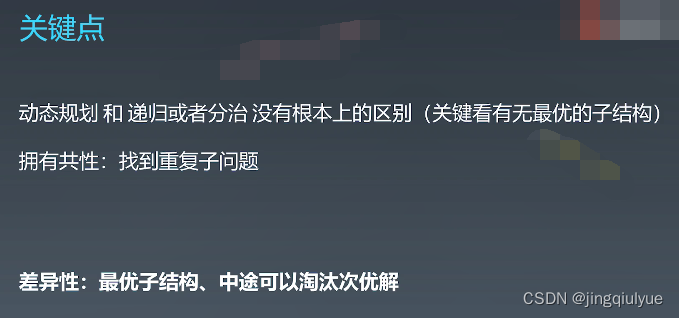
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
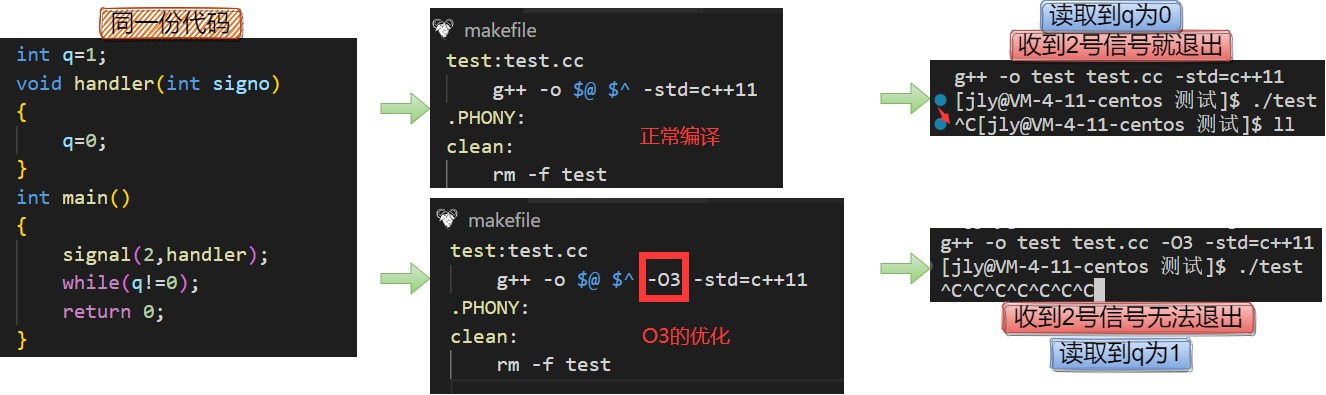
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...
C++回顾(二十一)—— list容器
21.1 list概述 list是一个双向链表容器,可高效地进行插入删除元素。list不可以随机存取元素,所以不支持at.(pos)函数与[]操作符。It(ok) it5(err)需要添加头文件:#include <list> 21.2 list构造 (1)默认构造…...

爱国者一体机电脑蓝屏怎么U盘重装系统教学?
爱国者一体机电脑蓝屏怎么U盘重装系统教学?有用户使用的爱国者一体机电脑开机了之后突然变成了蓝屏的了。而且无法继续使用了,那么遇到这样的蓝屏问题怎么去进行系统的重装呢?一起来看看以下的U盘重装系统教学吧。 准备工作: 1、U…...
)
Vue学习笔记(9)
9.1 axios 9.1.1 概述 Axios是一个流行的基于Promise的HTTP客户端,用于在浏览器和Node中发送HTTP请求。它可以用于处理各种请求类型,例如GET,POST等。Axios可以很容易地与现代前端框架和库集成,例如React,Vue等。 A…...
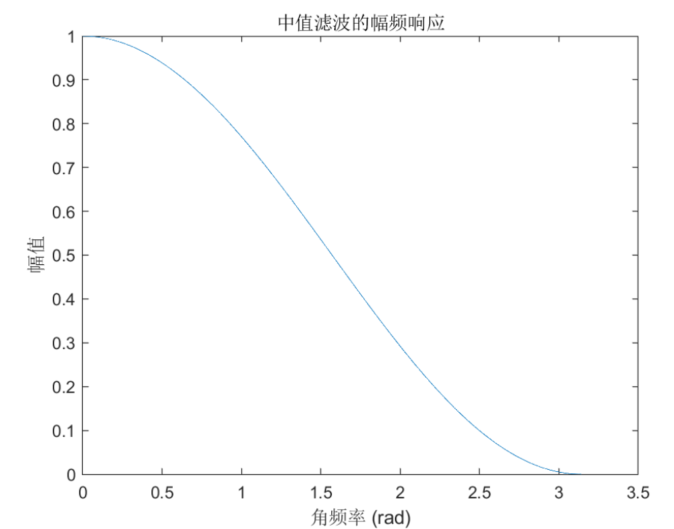
中值滤波+Matlab仿真+频域响应分析
中值滤波 文章目录中值滤波理解中值滤波的过程Matlab 实现实际应用频域分析中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序&…...

自然语言处理中数据增强(Data Augmentation)技术最全盘点
与“计算机视觉”中使用图像数据增强的标准做法不同,在NLP中,文本数据的增强非常少见。这是因为对图像的琐碎操作(例如将图像旋转几度或将其转换为灰度)不会改变其语义。语义上不变的转换的存在是使增强成为Computer Vision研究中…...
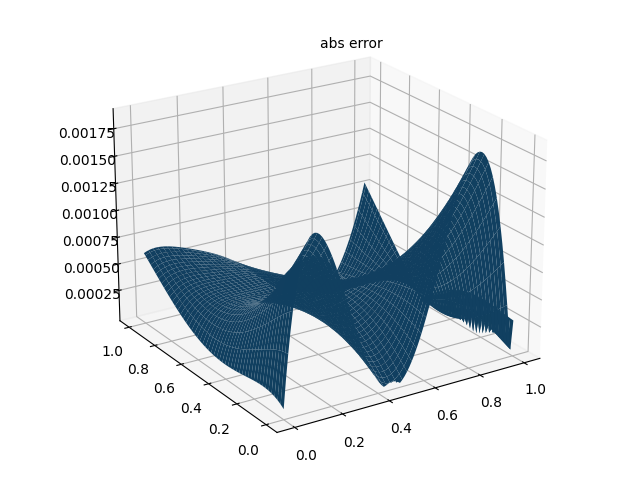
PINN解偏微分方程实例1
PINN解偏微分方程实例11. PINN简介2. 偏微分方程实例3. 基于pytorch实现代码4. 数值解参考资料1. PINN简介 PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。 ∂u∂tu∂u∂xv∂2u∂x2\begin{align} \frac{…...

【python 基础篇 十二】python的函数-------函数生成器
目录1.生成器基本概念2.生成器的创建方式3.生成器的输出方式4.send()方法5.关闭生成器6.注意事项1.生成器基本概念 是一个特色的迭代器(迭代器的抽象层级更高)所以拥有迭代器的特性 惰性计算数据 节省内存 ----就是不是立马生成所有数据,而是…...
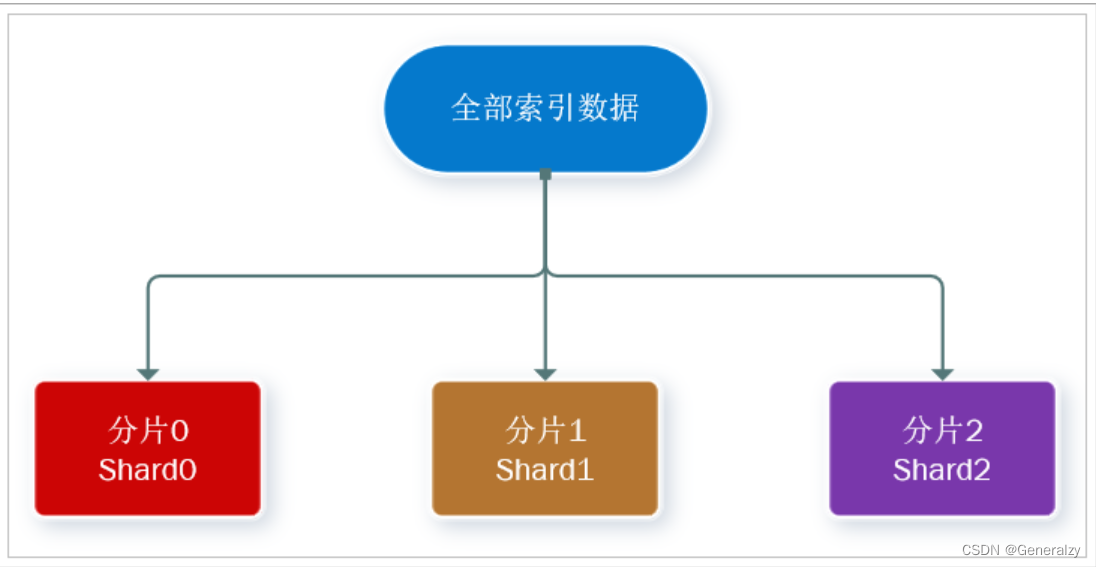
elasticsearch全解 (待续)
目录elasticsearchELK技术栈Lucene与Elasticsearch关系为什么不是其他搜索技术?Elasticsearch核心概念Cluster:集群Node:节点Shard:分片Replia:副本全文检索倒排索引正向和倒排es的一些概念文档和字段索引和映射mysql与…...

springboot2集成knife4j
springboot2集成knife4j springboot2集成knife4j 环境说明集成knife4j 第一步:引入依赖第二步:编写配置类第三步:测试一下 第一小步:编写controller第二小步:启动项目,访问api文档 相关资料 环境说明 …...

Qt 性能优化:CPU占有率高的现象和解决办法
一、前言 在最近的项目中,发现执行 Qt 程序时,有些情况下的 CPU 占用率奇高,最高高达 100%。项目跑在嵌入式板子上,最开始使用 EGLFS 插件,但是由于板子没有单独的鼠标层,导致鼠标移动起来卡顿,…...

MySQL专题(学会就毕业)
MySQL专题0.准备sql设计一张员工信息表,要求如下:编号(纯数字)员工工号 (字符串类型,长度不超过10位)员工姓名(字符串类型,长度不超过10位)性别(男/女,存储一…...

Java高级技术:单元测试、反射、注解
目录 单元测试 单元测试概述 单元测试快速入门 单元测试常用注解 反射 反射概述 反射获取类对象 反射获取构造器对象 反射获取成员变量对象 反射获取方法对象 反射的作用-绕过编译阶段为集合添加数据 反射的作用-通用框架的底层原理 注解 注解概述 自定义注解 …...

C语言初识
#include <stdio.h>//这种写法是过时的写法 void main() {}//int是整型的意思 //main前面的int表示main函数调用后返回一个整型值 int main() {return 0; }int main() { //主函数--程序的入口--main函数有且仅有一个//在这里完成任务//在屏幕伤输出hello world//函数-pri…...

Cadence Allegro 导出Etch Length by Layer Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Etch Length by Layer Report作用3,Etch Length by Layer Report示例4,Etch Length by Layer Report导出方法4.2,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
