算法08 广/宽度优先搜索及相关问题详解
这是《C++算法宝典》算法篇的第08节文章啦~
如果你之前没有太多C++基础,请点击👉专栏:C++语法入门,如果你C++语法基础已经炉火纯青,则可以进阶算法👉专栏:算法知识和数据结构👉专栏:数据结构啦
目录
📕广搜走迷宫找最短路径
📕如何找到最短路径?
🧠问题建模
如何表示迷宫地图等信息呢?
如何表示每次移动的过程?
如何实现搜索的过程呢?
问题参考程序
🧠广度优先搜索模板
📕训练:森林救援
参考代码
广搜走迷宫找最短路径
现在有一个4*4的迷宫,小知在迷宫的左上角,迷宫出口在右下角,小知体力有限,他希望尽快走出迷宫,请你告诉小知最少需要走多少步(每个格子不能重复走动)。

迷宫中显示0的点,是不可以走的。小知每次只能到达相邻的上下左右4个格子。
如何找到最短路径?
我们可以按照这样的思路去找:
- 从起点出发,检查第1步可以到达的所有点,判断是否为终点。
- 依次从第1步到达的点出发, 检查判断第2步可以到达的点是否为终点。
- 依次从第2步到达的点出发,检查判断第3步可以到达的点是否为终点。
- 依次从第3步到达的点出发,检查判断第4步可以到达的点是否为终点。
- 依次从第4步到达的点出发,检查判断第5步可以到达的点是否为终点。
6.找到终点,程序结束,步数为5。
问题建模
如何表示迷宫地图等信息呢?
1.使用一个4*4的二维数组maze[][]来存储迷宫信息,如果值位0表示不可走,1表示可走。
2.使用一个4*4的二维数组used[][]来标记是否走过,没走过为0,走过的话为1。
例:used[1][2]=1,表示maze[1][2]已经走过。
如何表示每次移动的过程?
每次移动,实际上就是坐标的变化。
上:行标-1,列标不变。
下:行标+1,列标不变。
左:行标不变,列标-1。
右:行标不变,列标+1。
我们可以用一个二维数组表示移动的方向。
例:当前坐标为(1,2),向上移动就是:
(1+fx[0][0],2+fx[0][1])得到(0,2)。
如何实现搜索的过程呢?
1.我们需要使用队列(que)来实现,用一个结构体表示每次找到的点的坐标信息以及步数(x,y,cnt)。
2.将起点入队。
3.取出队首元素,队首后移(head++),将队首元素上下左右的四个点依次入队(步数cnt要+1),同时判断是否到达终点,若到达终点则终止程序。
4.重复步骤3,直到找到终点或者队列为空(即head>tail)
问题参考程序
#include<bits/stdc++.h>
using namespace std;
struct wz{int x,y; //坐标int cnt; //步数
} que[1000],front,a; // front用来存每次取出的队首元素,a存起点信息
int maze[5][5],used[5][5];
int fx[4][2]={{0,-1},{0,1},{-1,0},{1,0}};
int head=1,tail=1,sx=1,sy=1,ex=3,ey=4,flag=0;//sx,sy,ex,ey分别表示开始,结束的坐标
void bfs(wz a);
int main()
{for(int i=1;i<=4;i++)for(int j=1;j<=4;j++)cin>>maze[i][j];a.x=sx,a.y=sy,a.cnt=0;bfs(a);cout<<que[tail].cnt;return 0;
}
void bfs(wz a){que[head]=a;//起点入队used[a.x][a.y]=1;while(head<=tail){ //当队列非空时搜索front=que[head]; //取出队首head++;//队首出队for(int i=0;i<4;i++){ //检查队首元素四个方向的点int nx=front.x+fx[i][0], ny=front.y+fx[i][1];//下一次前进点的坐标if(nx>=1&&nx<=4&&ny>=1&&ny<=4&&!used[nx][ny]&&maze[nx][ny]){//点要在地图内,且未被走过,且非障碍tail++; //队尾后移used[nx][ny]=1; //标记用过que[tail].x=nx; que[tail].y=ny;que[tail].cnt=front.cnt+1; //点入队,步数+1}if(nx==ex&&ny==ey){ //到达终点head=tail+1;//退出while循环break;//退出for循环}}}
}
广度优先搜索模板
上面的走迷宫的过程就是一个广度优先搜索的过程:从初始状态出发->1次转移(1步)能够到达的所有状态->2次转移(2步)能够到达的所有状态...n次转移能到达的所有状态。
我们常用广度优先搜索处理两种问题:
1.最短路径问题。
2.是否有路线的问题。
void bfs(State a){队头指针 head=1,队尾指针 tail=1;起始状态a入队while(head<=tail){取出队首元素 State=que[head];队头指针后移 head++;尝试从队首元素出发可以得到的n个状态for(int i=1;i<=n;i++){if(满足条件){队尾后移,tail++状态入队,并标记}if(到达终点) {退出for和while循环。}}}
}
训练:森林救援
正在森林中探险的小知,收到了一个求救信号。森林中有人受伤了,小知需要尽快赶到伤者那里帮忙。森林可以看做是一个m*n的地图,k表示小知,p表示伤者,森林中可以行走的地方用'*'表示,其他符号表示不可走。
小知只能上下左右移动,请你告诉小知,他最少需要走多远。
【输入描述】第一行输入m和n,分别表示地图的行和列
第二行输入地图的内容,其中k表示小知的位置,p表示伤者的位置,*表示可以行走的地方,其他符号均不可行走
【输出描述】如果小知能走到伤者的位置,输出其最少距离
如果小知走不到伤者的位置,输出No
【输入样例】
4 4
k * * *
* & * *
* * * p
* * * *
【输出样例】
5
参考代码
#include<bits/stdc++.h>
using namespace std;
struct wz{int x,y;int cnt;
} que[1000],front,a;
char maze[40][40];
int fx[4][2]={{0,-1},{0,1},{1,0},{-1,0}},used[40][40];
int head=1,tail=1,m,n,flag=0;
void bfs(wz a);
int main()
{cin>>m>>n;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>maze[i][j];if(maze[i][j]=='k'){a.x=i; a.y=j; a.cnt=0;}}}bfs(a);if(flag)cout<<que[tail].cnt;elsecout<<"No";return 0;
}
void bfs(wz a){que[head]=a;while(head<=tail){front=que[head];head++;for(int i=0;i<4;i++) {int nx=front.x+fx[i][0];int ny=front.y+fx[i][1];if(!used[nx][ny]&&(maze[nx][ny]=='*'||maze[nx][ny]=='p')){tail++;used[nx][ny]=1;que[tail].x=nx;que[tail].y=ny;que[tail].cnt=front.cnt+1;}if(maze[nx][ny]=='p'){flag=1;head=tail+1;break;}}}
}从入门到算法,再到数据结构,查看全部文章请点击此处![]() http://www.bigbigli.com/
http://www.bigbigli.com/
相关文章:
算法08 广/宽度优先搜索及相关问题详解
这是《C算法宝典》算法篇的第08节文章啦~ 如果你之前没有太多C基础,请点击👉专栏:C语法入门,如果你C语法基础已经炉火纯青,则可以进阶算法👉专栏:算法知识和数据结构👉专栏ÿ…...

PyTorch 版本与 CUDA 版本的兼容性示例
PyTorch 1.9.0 及以上版本支持 CUDA 11.1。PyTorch 1.8.0 支持 CUDA 11.0。PyTorch 1.7.0 支持 CUDA 10.2。PyTorch 1.6.0 支持 CUDA 10.1。PyTorch 1.5.0 支持 CUDA 10.1。PyTorch 1.4.0 支持 CUDA 10.1。PyTorch 1.3.0 支持 CUDA 10.0。PyTorch 1.2.0 支持 CUDA 9.2。PyTorch…...

Selenium进行Web自动化滚动
在使用Selenium进行Web自动化时,计算页面内的滚动条位置或执行滚动操作通常涉及JavaScript执行。Selenium的WebDriver提供了执行JavaScript代码的功能,这可以用来获取滚动条的位置或滚动到页面上的特定位置。 获取滚动条位置 你可以使用JavaScript的wi…...

机器学习模型训练过程和预测过程 用孩子来生动的比喻 --九五小庞
训练过程:孩子在学习知识 想象一下,一个年幼的孩子刚开始学习新知识,这就像是机器学习的模型训练过程。 收集教材:孩子首先得到了一本教科书或一系列学习材料,这些材料就像机器学习中的数据集,包含了各种…...

【爱上C++】详解string类2:模拟实现、深浅拷贝
在上一篇文章中我们介绍了string类的基本使用,本篇文章我们将讲解string类一些常用的模拟实现,其中有很多细小的知识点值得我们深入学习。Let’s go! 文章目录 类声明默认成员函数构造函数析构函数拷贝构造函数深浅拷贝问题传统写法现代写法…...

狄克斯特拉算法
狄克斯特拉算法(Dijkstra’s algorithm)是一种用于在带权图中找到从单一源点到所有其他顶点的最短路径的算法。它适用于处理带有非负权值的图。 下面将详细解释算法的工作原理、时间复杂度以及如何通过优化数据结构来改进其性能。 狄克斯特拉算法的工作…...

2024推荐整理几个磁力导航网站可提供海量资源的
都2024现在网上找资源像流水得鱼一样,抓一大把结果很难吃,我通宵特意整理的网站,网上有许多磁力导航网站可以提供海量的磁力链接资源,以下是一些有效的磁力导航网站推荐: 磁力搜索 链接: 资源类型&#x…...

链式访问:C语言中的函数调用技巧
链式访问:C语言中的函数调用技巧 在C语言编程中,链式访问(chained calls)是一个常见的编程技巧,它允许你在一行代码中连续调用多个函数或方法。这种技巧不仅能够让代码更加简洁和易读,还能减少临时变量的使…...
-1个手机号多用户身份)
数据库设计(实战项目)-1个手机号多用户身份
一. 背景: 该需求是一个互联网医院的预约单场景,护士在小程序上申请患者查房预约单,医生在小程序上对预约单进行接单,护士开始查房后填写查房小结,客户需要对用户信息进行授权,医生查房后进行签字ÿ…...

vue+fineReport 使用前端搜索+报表显示数据
--fineReprot 将需要搜索的参数添加到模版参数 sql: --前端传递参数 注:因为每次点击搜索的结果需要不一样,还要传递一个时间戳的参数: let timesamp new Date().getTime()...

高阶面试-存储系统的设计
概述 分类 块存储 block storage文件存储 file storage对象存储 object storage 区别: 块存储 概述 位于最底层,块,是物理存储设备上数据存储的最小单位。硬盘(Hard Disk Drive,HDD)就属于块存储。常见的还有固态硬盘(SSD)、…...

柔性测斜仪:土木工程与地质监测的得力助手
在现代土木工程和地质工程领域,精确监测土壤和岩石的位移情况对于确保工程安全至关重要。柔性测斜仪作为一种高精度、稳定性和灵活性兼备的测量设备,已逐渐成为工程师和研究人员的得力助手。本文将深入探讨柔性测斜仪在多个关键领域的应用及其重要性。 点…...

数字资产和数据资产你真的了解吗?
数据作为新型生产要素,是数字化、网络化、智能化的基础,已快速融入生产、分配、流通、消费和社会服务管理等各环节,深刻改变着生产方式、生活方式和社会治理方式。 何为数据资产?即由个人或企业拥有或控制的,能为企业带…...
【每日一练】python运算符
1. 算术运算符 编写一个Python程序,要求用户输入两个数,并执行以下运算:加法、减法、乘法、求余、除法、以及第一个数的第二个数次方。将结果打印出来。 a input("请输入第一个数:") b input("请输入第二个数&…...
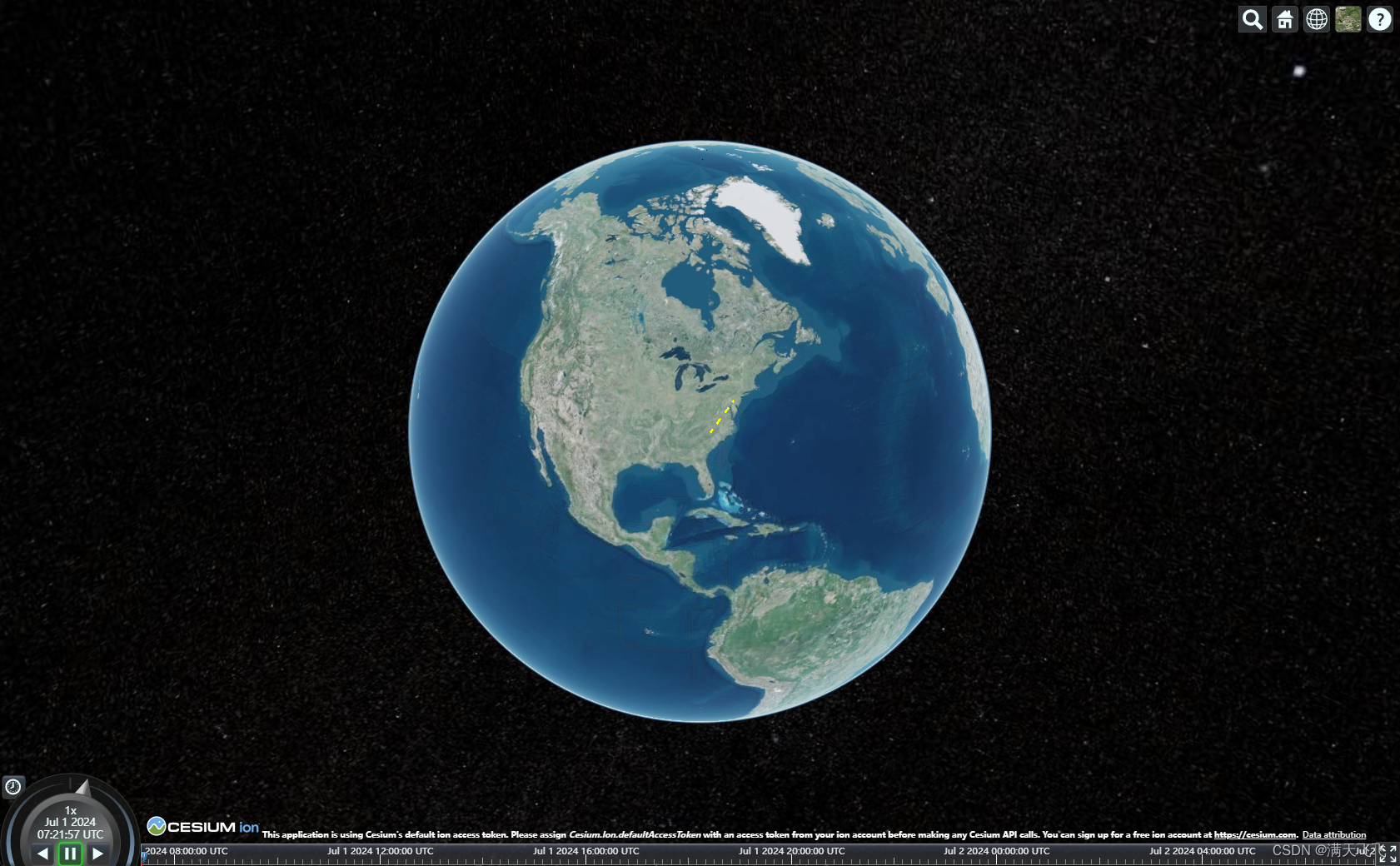
CesiumJS【Basic】- #032 绘制虚线(Primitive方式)
文章目录 绘制虚线(Primitive方式)1 目标2 代码2.1 main.ts绘制虚线(Primitive方式) 1 目标 使用Primitive方式绘制虚线 2 代码 2.1 main.ts // 定义线条的起点和终点var start = Cesium.Cartesian3.fromDegrees(-75.59777, 40.03883)...

海尔智家:科技优秀是一种习惯
海尔智家:科技优秀是一种习惯 2024-06-28 15:19代锡海 6月24日,2023年度国家科学技术奖正式揭晓。海尔智家“温湿氧磁多维精准控制家用保鲜电器技术创新与产业化”项目荣获国家科学技术进步奖,成为家电行业唯一牵头获奖企业。 很多人说&…...
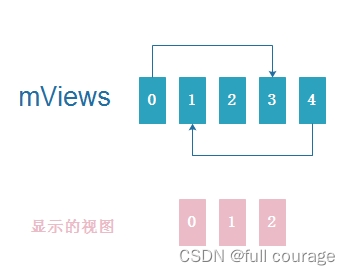
【Android】实现图片和视频混合轮播(无限循环、视频自动播放)
目录 前言一、实现效果二、具体实现1. 导入依赖2. 布局3. Banner基础配置4. Banner无限循环机制5. 轮播适配器6. 视频播放处理7. 完整源码 总结 前言 我们日常的需求基本上都是图片的轮播,而在一些特殊需求,例如用于展览的的数据大屏,又想展…...

VLAN基础
一、什么是Vlan VLAN(Virtual Local Area Network)是虚拟局域网的简称,是一种将单一物理局域网(LAN)在逻辑层面上划分为多个独立的广播域的技术。每个VLAN都是一个独立的广播域,其内部主机可以直接通信&am…...

pytest-yaml-sanmu(五):跳过执行和预期失败
除了手动注册标记之外,pytest 还内置了一些标记可直接使用,每种内置标记都会用例带来不同的特殊效果,本文先介绍 3 种。 1. skip skip 标记通常用于忽略暂时无法执行,或不需要执行的用例。 pytest 在执行用例时,如果…...
)
linux指令整合(centos系统持续更新中。。。)
1、查询java进程 ps -ef|grep java 2、查询端口占用 lsof -i:端口号 3、 启动java程序 java -jar jar包路径 后台启动 nohup java -jar jar包路径 -Xms512m -Xmx512m > 日志路径 2>&1 & 4、查看服务器资源占用 top 5、关闭进程 kill -9 进程号...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

