INS-GPS组合导航——卡尔曼滤波
系列文章目录
《SAR笔记-卫星轨道建模》
《SAR笔记-卫星轨迹(三维建模)》
《常用坐标系》
文章目录
前言
一、经典卡尔曼滤波
二、扩展卡尔曼滤波
三、无迹卡尔曼滤波
总结
前言
SAR成像仪器搭载于运动平台,平台的自定位误差将影响SAR图像质量。为保证SAR成像质量,需要长期精确且稳定的平台自定位轨迹,目前常见的定位系统包括惯导系统以及卫导系统。
惯性导航系统INS测量角度增量、速度增量等惯导参量,通过路径积分得到平台的位置、速度、姿态信息, 具有较高的短期测量精度,更新频率高,但惯导数据漂移,长期导航误差大。 全球定位系统GPS通过测量不同卫星与平台的时延差估计平台位置,具有良好的长期精度,但短期精度差,数据输出频率低,受星座构型、环境影响大。惯导系统测量量与卫导系统测量量之间相互联系,都能生成平台轨迹数据,但测量是相互独立的,因此可以用两套系统测得的数据进行融合,得到长期短期的稳定度以及精度都很高的平台轨迹信息。其中一种常见的数据融合算法就是卡尔曼滤波。
卡尔曼滤波本质上是一个数据融合算法,将具有同样测量目的、来自不同传感器、可能具有不同单位 (unit) 的数据融合在一起,得到一个更精确的目标估计值。本文简单介绍卡尔曼滤波的关键步骤,方便使用,关于步骤由来不做说明,网上的资料挺多的,可以根据自身需要学习。
一、经典卡尔曼滤波
经典卡尔曼滤波(Kalman Filter,KF)的局限性在于其只能拟合线性高斯系统。但其最大的优点在于计算量小,能够利用前一时刻的状态和当前时刻的测量值来得到当前时刻下的状态的最优估计。整个滤波算法主要涉及5个方程,分为两个阶段:预测阶段;校正阶段。
预测阶段涉及两个方程:
1、预测器方程(功能:由前一时刻的状态预测当前时刻的状态)
2、预测器协方差方程(功能:得到当前状态估计的协方差)
校正阶段涉及三个方程:
1、卡尔曼增益方程(功能:决定当前状态输出是更相信预测结果还是更相信测量结果)
2、状态更新方程(功能:卡尔曼滤波输出结果)
3、状态协方差更新(功能:更新状态的协方差更新)
除了上述主要方程,还涉及其他辅助方程:
1、测量方程(功能:描述状态量与测量量之间的关系)
考虑测量误差时,测量方程为
2、测量协方差(功能:描述测量量不确定性的,需要预先统计)
3、过程噪声协方差(功能:描述系统建模误差,比如理论上匀速直线运动的模型,在实际处理中会因为各种干扰很难匀速直线,导致真实轨迹并非匀速直线运动,而预测器方程基于匀速直线模型建立,这样产生的误差即为过程噪声协方差,包括系统输入
产生的影响,本文中
,需要预先统计)
4、估计协方差(功能:卡尔曼滤波输出结果的协方差)
其中更新后状态的协方差可以做如下化简
这个方程看起来要精炼很多并且容易记忆,并且在许多情况下没什么问题。但是,在计算卡尔曼增益时的一个小误差(浮点截尾误差)可能给结果带来巨大的偏差。的差可能因为浮点计算误差而使其结果不再是对称阵。这个方程在数值计算上并不稳定!
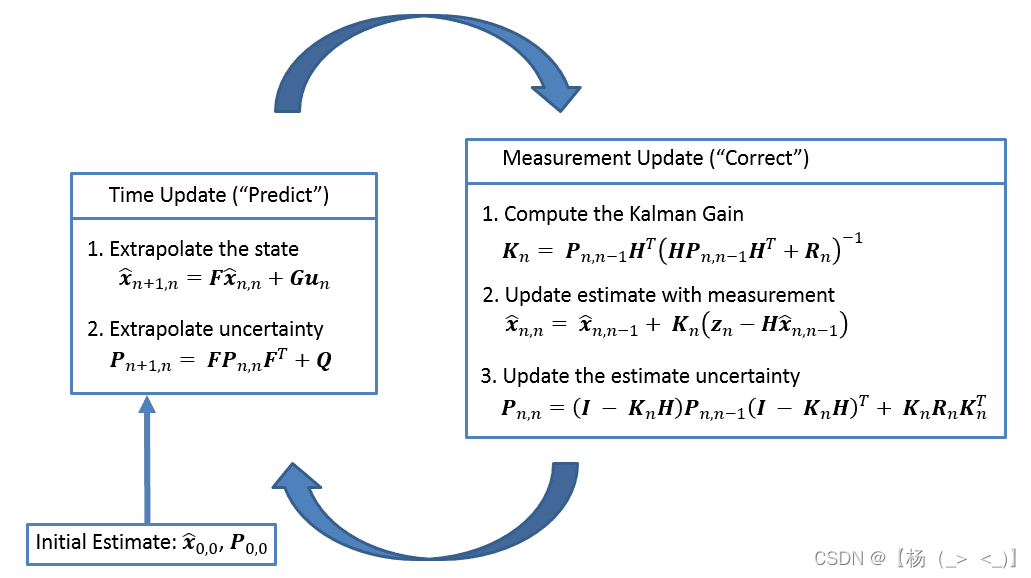
卡尔曼滤波算法流程如上图所示:一旦初始化完成,卡尔曼滤波首先预测下一时刻的系统状态,并且同时给出这个预测的不确定性。随后拿到测量结果,卡尔曼滤波会更新(或修正)这个预测值及其不确定性,并且同时再进行下一时刻的预测,以此类推。
二、扩展卡尔曼滤波
经典卡尔曼滤波解决的是经典的线性高斯系统的滤波问题。针对非线性系统,由于线性变换的关系不在了,因此预测量以及估计量的概率分布也不再是高斯分布。为了解决这类问题,人们利用非线性函数的局部线性特性,发明了扩展卡尔曼滤波(Extended Kalman Filter,EKF)。不考虑过程噪声以及噪声误差,非线性的状态转移方程以及观测为:
对函数f以及h进行泰勒展开并保留线性部分得
将非线性系统通过泰勒展开转换为动态变化的线性系统,扩展卡尔曼滤波与经典卡尔曼滤波类似,也包括:预测阶段;校正阶段。
预测阶段涉及两个方程:
1、预测器方程(功能:由前一时刻的状态预测当前时刻的状态)
2、预测器协方差方程(功能:得到当前状态估计的协方差)
其中;
校正阶段涉及三个方程:
1、卡尔曼增益方程(功能:决定当前状态输出是更相信预测结果还是更相信测量结果)
其中
2、状态更新方程(功能:卡尔曼滤波输出结果)
3、状态协方差更新(功能:更新状态的协方差更新)
扩展卡尔曼(EKF)与经典卡尔曼(KF)的区别在于测量矩阵H的计算。EKF对非线性函数进行泰勒展开后,进行一阶线性化的截断,忽略了其余高阶项,进而完成非线性函数的近似线性化。正是由于忽略了部分高阶项,使得EKF的状态估计会损失一些精度。因此,EHF 能否成功应用取决于两个因素:被近似的函数的局部非线性化程度;概率分布自身的不确定度(协方差)。
三、无迹卡尔曼滤波
无迹卡尔曼滤波(Unscented Kalman Filter,UKF)是一种非线性滤波算法,能够有效地处理复杂非线性系统的状态估计问题。其核心思想是通过一组选定的 sigma 点来逼近系统运动的高斯分布,从而实现状态估计。UKF算法通过选取 sigma 点,将系统的非线性映射转化为一组线性运算,然后利用卡尔曼滤波的思想进行状态估计。无迹卡尔曼滤波不采用泰勒展开实现非线性系统线性化,而是采用无迹变换(Unscented Transform,UT)来处理均值和协方差的非线性传递问题。
参考资料
卡尔曼滤波(Kalman Filtering)——(1)递归算法
Kalman滤波通俗理解+实际应用
卡尔曼滤波:从入门到精通
无人驾驶技术入门(十八)| 手把手教你写扩展卡尔曼滤波器
卡尔曼滤波
总结
本文主要介绍了经典卡尔曼滤波、扩展卡尔曼滤波,个人认为可以按照上述算法流程编写对应算法。从目前了解的信息,一般认为无迹卡尔曼滤波比前面两种卡尔曼滤波在非线性模型中的应用效果更好,后续根据学习情况更新无迹卡尔曼滤波。另外注明,本文为博主学习卡尔曼滤波的学习记录,内容上如果存在问题,欢迎评论区指出。转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。
相关文章:
INS-GPS组合导航——卡尔曼滤波
系列文章目录 《SAR笔记-卫星轨道建模》 《SAR笔记-卫星轨迹(三维建模)》 《常用坐标系》 文章目录 前言 一、经典卡尔曼滤波 二、扩展卡尔曼滤波 三、无迹卡尔曼滤波 总结 前言 SAR成像仪器搭载于运动平台,平台的自定位误差将影响SAR…...

day 58 739. 每日温度 496.下一个更大元素 I 503.下一个更大元素II
739. 每日温度 提示 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例…...
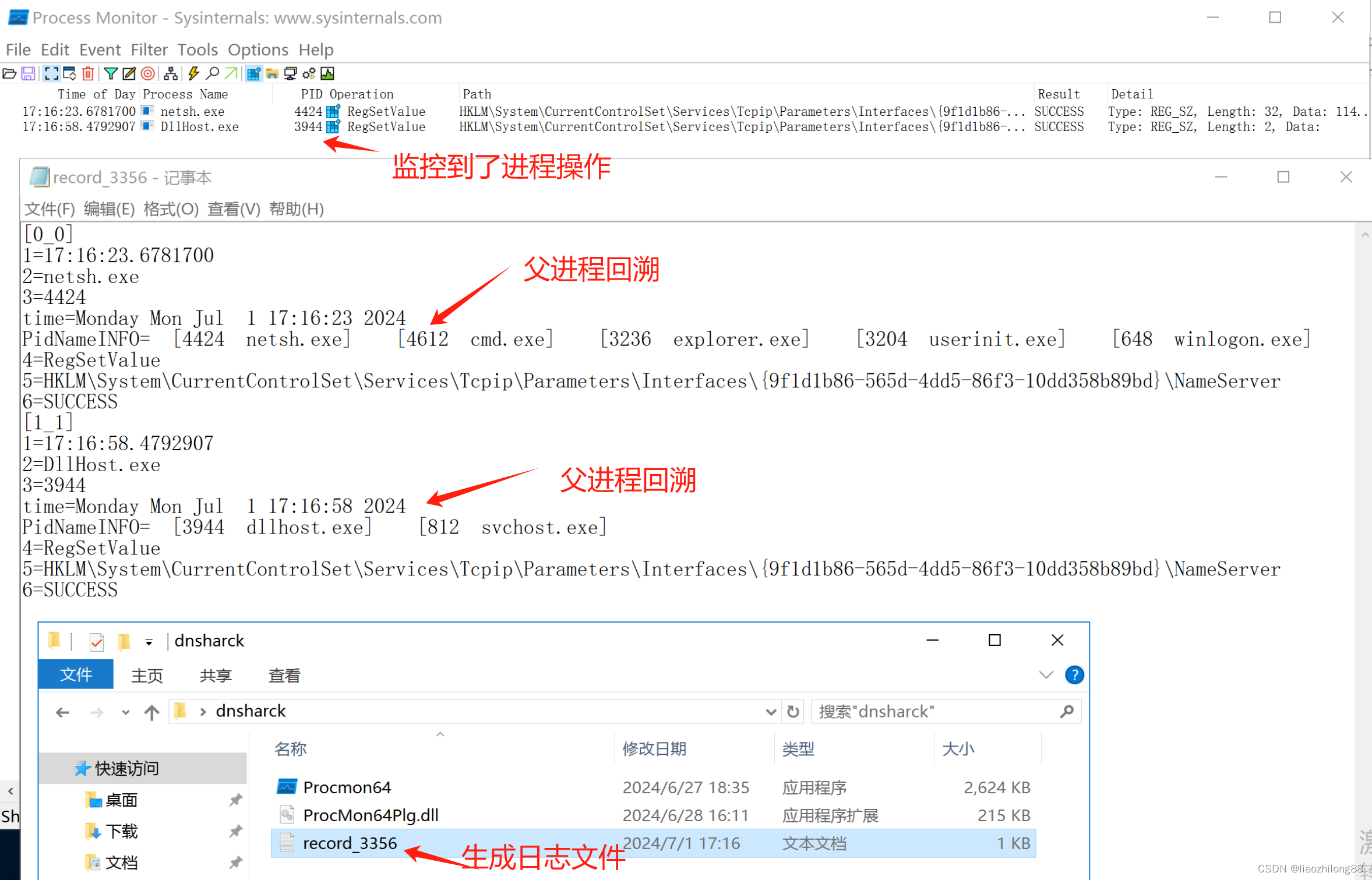
Dns被莫名篡改的问题定位(笔记)
引言:最近发现用户的多台机器上出现了Dns被莫名修改的问题,从系统事件上看并未能正常确定到是那个具体软件所为,现在的需求就是确定和定位哪个软件具体所为。 解决思路: 首先到IPv4设置页面对Dns进行设置:通过ProcExp…...

JVM原理(八):JVM虚拟机工具之基础故障工具
这里主要介绍监视虚拟机运行状态和进行故障处理的工具 1. jsp:虚拟机进程状况工具 jsp命令格式: jsp [options] [hostid] jps远程查询虚拟机进程状态 2. jstat:虚拟机统计信息监视工具 jstat命令格式: jstat [option vmid [interval [s|ms] [count]…...

Eureka的桥梁:服务消费者交互全解析
Eureka的桥梁:服务消费者交互全解析 在微服务架构中,服务发现是确保服务间有效通信的关键机制。Eureka,作为Netflix开源的服务发现框架,扮演着服务注册中心的角色,为服务消费者和服务提供者提供了一个动态的服务注册与…...
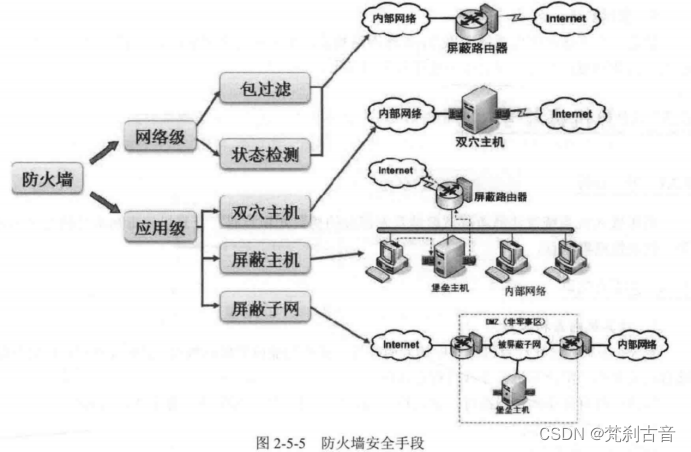
13_网络安全
目录 网络安全协议 网络安全协议 PGP协议 网络安全技术 防火墙技术 入侵检测系统 入侵防御系统 杀毒软件 蜜罐系统 计算机病毒与木马 网络安全协议 网络安全协议 物理层主要使用物理手段隔离、屏蔽物理设备等,其他层都是靠协议来保证传输的安全ÿ…...

C++ 中的数据类型
C规定在创建一个变量或者常量时,必须要指定出相应的数据类型,否则无法给变量分配内存. 1 整型 作用:整型变量表示的是整数类型的数据 C中能够表示整型的类型有以下几种方式,区别在于所占内存空间不同: 数据类型占用…...
CSS|04 复合选择器伪类选择器属性选择器美化超链接
基本选择器:见上篇基本选择器 复合选择器选择器1,选择器2{属性:值;} 多元素选择器,同时匹配选择器1和选择器2,多个选择器之间用逗号分隔举例: p,h1,h2{margin:0px;}E F{属性:值;} 后代元素选择器,匹配所有属于E元素后…...

探索Batch注释的奥秘:REM与::的细微差别
探索Batch注释的奥秘:REM与::的细微差别 在编写Batch文件时,注释是必不可少的部分,它们帮助我们理解代码的意图和逻辑。Batch脚本提供了两种添加注释的方法:REM命令和双冒号::。虽然它们功能相似,但在使用上存在一些细…...
 = a + aa + aaa + …aa…a (n 个 a)的和)
C语言 求数列 S(n) = a + aa + aaa + …aa…a (n 个 a)的和
求数列S(n)aaaaaa…aa…a(n个a)之值,其中a是一个数字,n表示a的位数,n由键盘输入。例如222222222222222(此时n5) 这个程序读取用户输入的一个数字 a 和一个正整数 n,计算并输出数列 S(n) 的值。 #include …...

MysqlDump
介绍:mysqldump是一个常用的命令行工具,它用于备份或导出MySQL或MariaDB数据库中的数据。这个工具可以创建一个SQL文件,其中包含数据库的结构和数据,这样就可以在其他MySQL服务器上重新创建数据库或进行数据迁移。 基本语法&#…...

某安全公司DDoS攻击防御2024年6月报告
引言: 在2024年6月,网络空间的安全挑战汹涌澎湃。分布式拒绝服务(DDoS)攻击频发,针对云服务、金融科技及在线教育平台的精密打击凸显出当前网络威胁环境的严峻性。 某安全公司作为网络安全防护的中坚力量,…...

Centos下rpm和yum执行卡住问题(已解决)
问题描述 执行rpm和yum卡住, 没有任何报错信息,且无法 ctrl c 终止,只能通过后台 kill -9 杀死。 问题排查: 查看yum日志:yum -vv 软件包 会发现卡在 loading keyring from rpmdb,即load DB存在问题。 …...

python自动化办公之PyPDF2.errors.DeprecationError
背景:pypdf2库在不断更新换代里面的类,逐渐淘汰一些旧的类 PyPDF2.errors.DeprecationError的意思是我们代码里用到的类计划被淘汰了,系统不推荐使用,解决办法:根据提示use xxx instead使用xxx 替换之前的类 例子1 P…...

[leetcode]first-unique-character-in-a-string 字符串中的第一个唯一字符
. - 力扣(LeetCode) class Solution { public:int firstUniqChar(string s) {unordered_map<int, int> frequency;for (char ch: s) {frequency[ch];}for (int i 0; i < s.size(); i) {if (frequency[s[i]] 1) {return i;}}return -1;} };...

使用uniapp.pageScrollTo方法进行页面滚动
先看看是不是你想要的: 需求: 有个填写数据的单子在提交的时候,会对必填项做校验,如果必填项没有数据的话,必填项校验生效给出提示,并且页面滚动到第一个需要填写数据的地方。 开发: 因为这个…...

寒武纪实现高维向量的softmax进阶优化和库函数对比
关于寒武纪编程可以参考本人之前的文章添加链接描述,添加链接描述,添加链接描述 实验证明,axis=0和axis=-1的时候,手写softmax速度可以和库函数媲美,甚至于更甚一筹。 src/softmax.mlu #include <bang.h> #include...
我的世界服务器-高版本服务器-MC服务器-生存服务器-RPG服务器-幻世星辰
生存为主,RPG乐趣为辅,重视每位玩家的建议,一起打造心目中的服务器,与小伙伴一起探险我的世界! 服务器版本: 1.18.2 ~ 1.20.4 Q群: 338238381 服务器官网: 星辰毛毛雨-Minecraft高版本生存服务器我的世界…...

倒装COB显示屏与传统SMD显示屏安装方式有哪些不同?
COB显示屏与传统SMD显示屏是商业显示领域中非常重要的两种载体,在前面的文章当中我们为大家阐述了倒装COB显示屏的技术特点,今天跟随COB显示屏厂家深圳市中品瑞科技一起来看看,COB显示屏的安装与传统LED显示屏的安装有哪些不同? 一…...
elasticsearch重置密码
0 案例背景 Elasticsearch三台集群环境,对外端口为6200,忘记elasticsearch密码,进行重置操作 注:若无特殊说明,三台服务器均需进行处理操作 1 停止es /rpa/bin/elasticsearch.sh stop 检查状态 ps -ef|grep elast…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
