基于隐马尔可夫模型的股票预测【HMM】
基于机器学习方法的股票预测系列文章目录
一、基于强化学习DQN的股票预测【股票交易】
二、基于CNN的股票预测方法【卷积神经网络】
三、基于隐马尔可夫模型的股票预测【HMM】
文章目录
- 基于机器学习方法的股票预测系列文章目录
- 一、HMM模型简介
- (1)前向后向算法
- (2)概率计算
- (3)对数似然函数
- (4)Baum-Welch算法
- (5)预测下一个观测值
- (6)Kmeans参数初始化
- 二、Python代码分析
- (1)高斯分布函数
- (2)GaussianHMM 类
- 1 初始化
- 2 K-means参数初始化
- 3 前向算法
- 4 后向算法
- 5 观测概率计算
- 6 Baum-Welch算法
- 7 预测
- 8 预测更多时刻
- 9 解码
- (3)总结
- 三、实验分析
- (1)对股票指数建模的模型参数
- (2)不同states下的对数似然变化
- (3)不同states下的股票指数拟合效果
- (4)不同states下的误差及MSE
- (5)HMM模型单支股票预测小结
- (6)多支股票训练模型
本文探讨了利用隐马尔可夫模型(Hidden Markov Model, HMM)进行股票预测的建模方法,并详细介绍了模型的原理、参数初始化以及实验分析。HMM模型通过一个隐藏的马尔可夫链生成不可观测的状态序列,并由这些状态生成观测序列。本文假设观测概率分布为高斯分布,并利用前向后向算法进行概率计算和参数估计,完整代码放在GitHub上——Stock-Prediction-Using-Machine-Learing。
一、HMM模型简介
隐马尔可夫模型 (Hidden Markov Model, HMM模型), 是关于时序的概率模型, 描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列, 再由各个状态生成一个观测而产生观测随机序列的过程。HMM模型有两个基本假设:
- 齐次马尔可夫性假设: 即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态, 与其他时刻的状态及观测无关, 也与时刻 t无关。
- 观测独立性假设: 即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
隐马尔可夫模型由初始概率分布 π \pi π 、状态转移概率分布 A A A 以及观测概率分布 B B B 确定, 故可将隐马尔可夫模型 λ \lambda λ 用三元符号表示:
λ = ( A , B , π ) \lambda=(A, B, \pi) λ=(A,B,π)
在本次股票预测中, 可假设观测概率分布为:
P ( x ∣ i ) = 1 ( 2 π ) d ∣ Σ i ∣ exp ( − 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) ) P(x \mid i)=\frac{1}{\sqrt{(2 \pi)^{d}\left|\Sigma_{i}\right|}} \exp \left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)^{T} \Sigma_{i}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\right) P(x∣i)=(2π)d∣Σi∣1exp(−21(x−μi)TΣi−1(x−μi))
由此得到高斯隐马尔可夫模型。
股票价格是可以看作连续值,所以利用隐马尔可夫模型对股票进行建模时,假设观测概率为高斯分布,然后便可以进行HMM模型参数估计、相应的概率计算,详细原理下面展开叙述。
(1)前向后向算法
前向算法: 给定隐马尔可夫模型 λ \lambda λ, 定义到时刻t部分观测序列为 x 1 , x 2 , ⋯ ⋯ , x t x_{1}, x_{2}, \cdots \cdots, x_{t} x1,x2,⋯⋯,xt, 且状态为 i的概率为前向概率, 记作:
α t ( i ) = P ( x 1 , x 2 , ⋯ , x t , i t = i ∣ λ ) \alpha_{t}(i)=P\left(x_{1}, x_{2}, \cdots, x_{t}, i_{t}=i \mid \lambda\right) αt(i)=P(x1,x2,⋯,xt,it=i∣λ)
后向算法: 给定隐马尔可夫模型 λ \lambda λ, 定义到时刻t部分观测序列为 x 1 , x 2 , ⋯ ⋯ , x t \mathrm{x}_{1}, \mathrm{x}_{2}, \cdots \cdots, \mathrm{x}_{t} x1,x2,⋯⋯,xt, 且状态为 i \mathrm{i} i 的概率为后向概率, 记作
β t ( i ) = P ( x t + 1 , x t + 2 , ⋯ , x T ∣ i t = i , λ ) \beta_{t}(i)=P\left(x_{t+1}, x_{t+2}, \cdots, x_{T} \mid i_{t}=i, \lambda\right) βt(i)=P(xt+1,xt+2,⋯,xT∣it=i,λ)
为避免计算过程中数值的上溢与下溢, 作如下处理, 令:
S α , t = 1 max i α t ( i ) , S β , t = 1 max i β t ( i ) α t ( i ) = S α , t α t ( i ) , β t ( i ) = S β , t β t ( i ) \begin{aligned} S_{\alpha, t} &=\frac{1}{\max _{i} \alpha_{t}(i)}, S_{\beta, t}=\frac{1}{\max _{i} \beta_{t}(i)} \\ \alpha_{t}(i) &=S_{\alpha, t} \alpha_{t}(i), \beta_{t}(i)=S_{\beta, t} \beta_{t}(i) \end{aligned} Sα,tαt(i)=maxiαt(i)1,Sβ,t=maxiβt(i)1=Sα,tαt(i),βt(i)=Sβ,tβt(i)
(2)概率计算
推导可知, 给定模型 λ \lambda λ 和观测 O O O, 在时刻 t t t 处于i的概率记为:
γ t ( i ) = α t ( i ) β t ( i ) ∑ j α t ( j ) β t ( j ) \gamma_{t}(i)=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{j} \alpha_{t}(j) \beta_{t}(j)} γt(i)=∑jαt(j)βt(j)αt(i)βt(i)
给定模型 λ \lambda λ 和观测 O O O, 在时刻 t t t 处于状态i且在时刻 t + 1 \mathrm{t}+1 t+1 处于状态 j \mathrm{j} j 的概率记为:
γ t , t + 1 ( i , j ) = α t ( i ) P ( j ∣ i ) β t + 1 ( j ) P ( x t + 1 ∣ j ) ∑ k , l α t ( k ) P ( l ∣ k ) β t + 1 ( l ) P ( x t + 1 ∣ l ) \gamma_{t, t+1}(i, j)=\frac{\alpha_{t}(i) P(j \mid i) \beta_{t+1}(j) P\left(\boldsymbol{x}_{t+1} \mid j\right)}{\sum_{k, l} \alpha_{t}(k) P(l \mid k) \beta_{t+1}(l) P\left(\boldsymbol{x}_{t+1} \mid l\right)} γt,t+1(i,j)=∑k,lαt(k)P(l∣k)βt+1(l)P(xt+1∣l)αt(i)P(j∣i)βt+1(j)P(xt+1∣j)
(3)对数似然函数
在利用最大似然对HMM模型进行参数估计的时候,其对数似然函数如下:
L = log P ( O ∣ λ ) = log ∑ i = 1 N α T ( i ) \begin{aligned} L &=\log P(O \mid \lambda) \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i) \end{aligned} L=logP(O∣λ)=logi=1∑NαT(i)
因为每次进行了归一化:
α t ( i ) = S α , t ⋅ α t ( i ) \alpha_{t}(i)=S_{\alpha, t} \cdot \alpha_{t}(i) αt(i)=Sα,t⋅αt(i)
递推到T时,可得:
α T ( i ) = S α , 1 ⋅ S α , 2 ⋯ S α , T ⋅ α T ( i ) \alpha_{T}(i)=S_{\alpha, 1} \cdot S_{\alpha, 2} \cdots S_{\alpha, T} \cdot \alpha_{T}(i) αT(i)=Sα,1⋅Sα,2⋯Sα,T⋅αT(i)
故最终对数似然函数为:
L = log P ( O ∣ λ ) = log ∑ i = 1 N α T ( i ) = log ∑ i = 1 N α T ( i ) Π i = 1 T S α , i = log ∑ i = 1 N α T ( i ) − ∑ i = 1 T log S α , i \begin{aligned} L &=\log P(O \mid \lambda) \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i) \\ &=\log \sum_{i=1}^{N} \frac{\alpha_{T}(i)}{\Pi_{i=1}^{T} S_{\alpha, i}} \\ &=\log \sum_{i=1}^{N} \alpha_{T}(i)-\sum_{i=1}^{T} \log S_{\alpha, i} \end{aligned} L=logP(O∣λ)=logi=1∑NαT(i)=logi=1∑NΠi=1TSα,iαT(i)=logi=1∑NαT(i)−i=1∑TlogSα,i
(4)Baum-Welch算法
模型参数的学习问题,即给定观测序列 O = { O 1 , O 2 , … , O T } O=\{O_1,O_2,…,O_T\} O={O1,O2,…,OT},估计模型 λ = ( A , B , π ) λ=(A,B,\pi) λ=(A,B,π)的参数,对HMM模型参数的估计可以由监督学习和非监督学习的方法实现,而Baum-Welch算法是监督学习的方法。Baum-Welch算法是EM算法在隐马尔可夫模型学习中的具体实现, 由BW算法可推知隐马尔可夫模型的参数递推表达式:
- 初始状态概率向量: π ( i ) = ∑ X γ 1 X ( i ) ∑ X 1 \pi(i)=\frac{\sum_{X} \gamma_{1}^{X}(i)}{\sum_{X} 1} π(i)=∑X1∑Xγ1X(i)
- 状态转移概率矩阵: P ( j ∣ i ) = ∑ t = 1 T − 1 γ t , t + 1 ( i , j ) ∑ t = 1 T − 1 γ t ( i ) P(j \mid i)=\frac{\sum_{t=1}^{T-1} \gamma_{t, t+1}(i, j)}{\sum_{t=1}^{T-1} \gamma_{t}(i)} P(j∣i)=∑t=1T−1γt(i)∑t=1T−1γt,t+1(i,j)
- 观测概率矩阵:
μ i = ∑ t γ t ( i ) x t ∑ t γ t ( i ) , Σ i = ∑ t γ t ( i ) ( x t − μ i ) ( x t − μ i ) T ∑ t γ t ( i ) \boldsymbol{\mu}_{i}=\frac{\sum_{t} \gamma_{t}(i) \boldsymbol{x}_{t}}{\sum_{t} \gamma_{t}(i)}, \Sigma_{i}=\frac{\sum_{t} \gamma_{t}(i)\left(\boldsymbol{x}_{t}-\mu_{i}\right)\left(\boldsymbol{x}_{t}-\mu_{i}\right)^{T}}{\sum_{t} \gamma_{t}(i)} μi=∑tγt(i)∑tγt(i)xt,Σi=∑tγt(i)∑tγt(i)(xt−μi)(xt−μi)T
通过前后向算法可以得到相应的概率值,然后将相应的概率值代入上面的递推表达式,进行迭代便可以得到HMM模型的参数。
(5)预测下一个观测值
由 α t ( i ) \alpha_{\mathrm{t}}(i) αt(i) 的定义, 给定观测序列 x 1 : t \boldsymbol{x}_{1: t} x1:t, 状态为 i \mathrm{i} i 的概率为:
P ( i ∣ x 1 : t ) = α t ( i ) ∑ j α t ( j ) P\left(i \mid \boldsymbol{x}_{1: t}\right)=\frac{\alpha_{t}(i)}{\sum_{j} \alpha_{t}(j)} P(i∣x1:t)=∑jαt(j)αt(i)
则给定观测序列 x 1 : t , t + 1 x_{1: t}, t+1 x1:t,t+1 时刻伏态为 j \mathrm{j} j 的概率为: ∑ i P ( i ∣ x 1 : t ) P ( j ∣ i ) \sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) P(j \mid i) ∑iP(i∣x1:t)P(j∣i), 从而由全概率公式, t + 1 t+1 t+1 时刻观测值为 x t + 1 \boldsymbol{x}_{\boldsymbol{t}+1} xt+1 的概率为:
P ( x t + 1 ∣ x 1 : t ) = ∑ j P ( x ∣ j ) ∑ i P ( i ∣ x 1 : t ) P ( j ∣ i ) P\left(\boldsymbol{x}_{t+1} \mid \boldsymbol{x}_{1: t}\right)=\sum_{j} P(\boldsymbol{x} \mid j) \sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) P(j \mid i) P(xt+1∣x1:t)=j∑P(x∣j)i∑P(i∣x1:t)P(j∣i)
由最小均方误差估计(MMSE), 可得 t + 1 t+1 t+1 时刻观测值 x t + 1 x_{t+1} xt+1 的估计值为:
x ^ t + 1 = E [ x t + 1 ∣ x 1 : t ] \hat{\boldsymbol{x}}_{t+1}=E\left[\boldsymbol{x}_{t+1} \mid \boldsymbol{x}_{1: t}\right] x^t+1=E[xt+1∣x1:t]
即:
x ^ t + 1 = ∑ i P ( i ∣ x 1 : t ) ∑ j P ( j ∣ i ) E ( x ∣ j ) \hat{\boldsymbol{x}}_{t+1}=\sum_{i} P\left(i \mid \boldsymbol{x}_{1: t}\right) \sum_{j} P(j \mid i) E(\boldsymbol{x} \mid j) x^t+1=i∑P(i∣x1:t)j∑P(j∣i)E(x∣j)
(6)Kmeans参数初始化
在利用HMM可夫模型进行建模的过程中,我们发现模型对参数的初始化十分敏感,不同的初始化最后得到的模型效果差异非常的,经过不同的方法尝试,我们发现利用Kmeans的方法对模型进行初始化,效果非常好。利用Kmeans初始化的步骤如下:
- 选定HMM模型隐状态数n
- 将股票收盘价数据聚为n类
- 令模型参数中观测矩阵的初始均值=聚类中心的值
二、Python代码分析
Github上的hmm.py文件实现了一个高斯隐马尔可夫模型(Gaussian Hidden Markov Model, GaussianHMM)用于时间序列数据的建模和预测。模型通过EM算法(Baum-Welch算法)进行参数估计,并包含前向后向算法、预测和解码等功能,主要函数和方法如下。
(1)高斯分布函数
def gauss2D(x, mean, cov):z = -np.dot(np.dot((x-mean).T,inv(cov)),(x-mean))/2.0temp = pow(sqrt(2.0*pi),len(x))*sqrt(det(cov))return (1.0/temp)*exp(z)
该函数计算二元高斯分布的概率密度。输入为样本点x,均值mean和协方差矩阵cov。
(2)GaussianHMM 类
1 初始化
class GaussianHMM:def __init__(self, n_state=1, x_size=1, iter=20, if_kmeans=True):self.n_state = n_stateself.x_size = x_sizeself.start_prob = np.ones(n_state) * (1.0 / n_state)self.transmat_prob = np.ones((n_state, n_state)) * (1.0 / n_state)self.trained = Falseself.n_iter = iterself.observe_mean = np.zeros((n_state, x_size))self.observe_vars = np.zeros((n_state, x_size, x_size))for i in range(n_state): self.observe_vars[i] = np.random.randint(0,10)self.kmeans = if_kmeans
该函数初始化HMM模型的参数,包括隐状态数n_state、输入维度x_size、EM算法迭代次数iter、是否使用KMeans进行初始化if_kmeans等。
2 K-means参数初始化
def _init(self, X):mean_kmeans = cluster.KMeans(n_clusters=self.n_state)mean_kmeans.fit(X)if self.kmeans:self.observe_mean = mean_kmeans.cluster_centers_print("聚类初始化成功!")else:self.observe_mean = np.random.randn(self.n_state, 1) * 2print("随机初始化成功!")for i in range(self.n_state):self.observe_vars[i] = np.cov(X.T) + 0.01 * np.eye(len(X[0]))
通过K-means聚类方法对观测矩阵的均值进行初始化,并计算协方差矩阵。
3 前向算法
def forward(self, X):X_length = len(X)alpha = np.zeros((X_length, self.n_state))alpha[0] = self.observe_prob(X[0]) * self.start_probS_alpha = np.zeros(X_length)S_alpha[0] = 1 / np.max(alpha[0])alpha[0] = alpha[0] * S_alpha[0]for i in range(X_length):if i == 0:continuealpha[i] = self.observe_prob(X[i]) * np.dot(alpha[i - 1], self.transmat_prob)S_alpha[i] = 1 / np.max(alpha[i])if S_alpha[i] == 0:continuealpha[i] = alpha[i] * S_alpha[i]return alpha, S_alpha
计算前向概率,并进行归一化处理,防止数值上溢或下溢。
4 后向算法
def backward(self, X):X_length = len(X)beta = np.zeros((X_length, self.n_state))beta[X_length - 1] = np.ones((self.n_state))S_beta = np.zeros(X_length)S_beta[X_length - 1] = np.max(beta[X_length - 1])beta[X_length - 1] = beta[X_length - 1] / S_beta[X_length - 1]for i in reversed(range(X_length)):if i == X_length - 1:continuebeta[i] = np.dot(beta[i + 1] * self.observe_prob(X[i + 1]), self.transmat_prob.T)S_beta[i] = np.max(beta[i])if S_beta[i] == 0:continuebeta[i] = beta[i] / S_beta[i]return beta
计算后向概率,并进行归一化处理。
5 观测概率计算
def observe_prob(self, x):prob = np.zeros((self.n_state))for i in range(self.n_state):prob[i] = gauss2D(x, self.observe_mean[i], self.observe_vars[i])return prob
计算当前观测值在各个隐状态下的观测概率。
6 Baum-Welch算法
def train(self, X):self.trained = TrueX_length = len(X)self._init(X)print("开始训练")start_time = time.time()self.L = []for _ in tqdm(range(self.n_iter)):alpha, S_alpha = self.forward(X)beta = self.backward(X)L = np.log(np.sum(alpha[-1])) - np.sum(np.log(S_alpha))self.L.append(L)post_state = alpha * beta / (np.sum(alpha * beta, axis=1)).reshape(-1, 1)post_adj_state = np.zeros((self.n_state, self.n_state))for i in range(X_length):if i == 0:continuenow_post_adj_state = np.outer(alpha[i - 1], beta[i] * self.observe_prob(X[i])) * self.transmat_probpost_adj_state += now_post_adj_state / np.sum(now_post_adj_state)self.start_prob = post_state[0] / np.sum(post_state[0])for k in range(self.n_state):self.transmat_prob[k] = post_adj_state[k] / np.sum(post_adj_state[k])self.observe_prob_updated(X, post_state)total_time = time.time() - start_timeprint(f"训练完成,耗时:{round(total_time, 2)}sec")
通过Baum-Welch算法进行模型参数的估计。包括E步骤(计算前向后向概率和后验概率)和M步骤(更新模型参数)。
7 预测
def predict(self, origin_X, t):X = origin_X[:t]alpha, _ = self.forward(X)post_state = alpha / (np.sum(alpha, axis=1)).reshape(-1, 1)now_post_state = post_statex_pre = 0for state in range(self.n_state):p_state = now_post_state[:, state]temp = 0for next_state in range(self.n_state):temp += self.observe_mean[next_state] * self.transmat_prob[state][next_state]x_pre += p_state * tempreturn x_pre
预测时刻t的观测值。
8 预测更多时刻
def predict_more(self, origin_X, t):X = origin_X.copy()X_length = len(X)while X_length < t:alpha, _ = self.forward(X)post_state = alpha / (np.sum(alpha, axis=1)).reshape(-1, 1)now_post_state = post_statex_pre = 0for state in range(self.n_state):p_state = now_post_state[:, state]temp = 0for next_state in range(self.n_state):temp += self.observe_mean[next_state] * self.transmat_prob[state][next_state]x_pre += p_state * tempX = np.concatenate([X, x_pre[-1].reshape(-1, 1)])X_length += 1return X
预测更多时刻的观测值。
9 解码
def decode(self, X):X_length = len(X)state = np.zeros(X_length)pre_state = np.zeros((X_length, self.n_state))max_pro_state = np.zeros((X_length, self.n_state))max_pro_state[0] = self.observe_prob(X[0]) * self.start_probfor i in range(X_length):if i == 0:continuefor k in range(self.n_state):prob_state = self.observe_prob(X[i])[k] * self.transmat_prob[:, k] * max_pro_state[i - 1]max_pro_state[i][k] = np.max(prob_state)pre_state[i][k] = np.argmax(prob_state)state[X_length - 1] = np.argmax(max_pro_state[X_length - 1, :])for i in reversed(range(X_length)):if i == X_length - 1:continuestate[i] = pre_state[i + 1][int(state[i + 1])]return state
利用维特比算法解码观测序列,求其最可能的隐藏状态序列。
(3)总结
该代码实现了一个功能完备的高斯隐马尔可夫模型(GaussianHMM),包括初始化、前向后向算法、Baum-Welch算法进行参数估计、预测和解码等功能。通过K-means聚类进行初始化可以提高模型的初始参数设置,从而提高模型的训练效果。
三、实验分析
(1)对股票指数建模的模型参数
以DJ指数的收盘价为观测序列, 隐状态数量states分别设为 4 , 8 , 16 , 32 4,8,16,32 4,8,16,32, 我们得到了不同情况下的HMM模型, 其中以states = 8 =8 =8 为例, 学习得到的参数为:
初始概率分布: ( 0.000044 0.000000 0.000000 0.000000 0.000000 0.000000 0.999956 ) (\begin{array}{lllllll}0.000044 & 0.000000 & 0.000000 & 0.000000 & 0.000000 & 0.000000 &0.999956\end{array}) (0.0000440.0000000.0000000.0000000.0000000.0000000.999956)
状态转移概率矩阵: ( 0.9498 0 0 0 0 0 0.0317 0.0185 0 0.9729 0 0 0.0158 0.0113 0 0 0 0 0.9433 0 0 0.0205 0.0362 0 0 0 0 0.9923 0.0077 0 0 0 0 0.0338 0 0.0178 0.9484 0 0 0 0 0.0091 0.0136 0 0 0.9773 0 0 0.0242 0 0.0296 0 0 0 0.9462 0 0.0238 0 0 0 0 0 0 0.9762 ) \left(\begin{array}{rrrrrrrr}0.9498 & 0 & 0 & 0 & 0 & 0 & 0.0317 & 0.0185 \\ 0 & 0.9729 & 0 & 0 & 0.0158 & 0.0113 & 0 & 0 \\ 0 & 0 & 0.9433 & 0 & 0 & 0.0205 & 0.0362 & 0 \\ 0 & 0 & 0 & 0.9923 & 0.0077 & 0 & 0 & 0 \\ 0 & 0.0338 & 0 & 0.0178 & 0.9484 & 0 & 0 & 0 \\ 0 & 0.0091 & 0.0136 & 0 & 0 & 0.9773 & 0 & 0 \\ 0.0242 & 0 & 0.0296 & 0 & 0 & 0 & 0.9462 & 0 \\ 0.0238 & 0 & 0 & 0 & 0 & 0 & 0 & 0.9762\end{array}\right) 0.9498000000.02420.023800.9729000.03380.009100000.9433000.01360.029600000.99230.017800000.015800.00770.948400000.01130.0205000.9773000.031700.03620000.946200.01850000000.9762
观测概率分布:
-
均值: ( 12519.93 9640.24 10388.37 13541.56 13009.42 12052.83 8276.14 11241.26 ) (\begin{array}{llllllll}12519.93 & 9640.24 & 10388.37 & 13541.56 & 13009.42 & 12052.83 & 8276.14 & 11241.26\end{array}) (12519.939640.2410388.3713541.5613009.4212052.838276.1411241.26)
-
协方差: ( 23834.89 71700.85 45532.26 57449.12 26262.64 28852.07 338454.89 68110.31 ) (23834.89 \quad 71700.85 \quad 45532.26 \quad 57449 .12 \quad 26262.64 \quad 28852.07 \quad 338454.89 \quad 68110 .31) (23834.8971700.8545532.2657449.1226262.6428852.07338454.8968110.31)
我们可以看到模型最终参数中观测概率分布中的均值和一开始聚类初始化的均值十分接近,这也是为什么Kmeans均值初始化效果非常好的原因。
(2)不同states下的对数似然变化
不同states下的对数似然变化情况如下图所示:
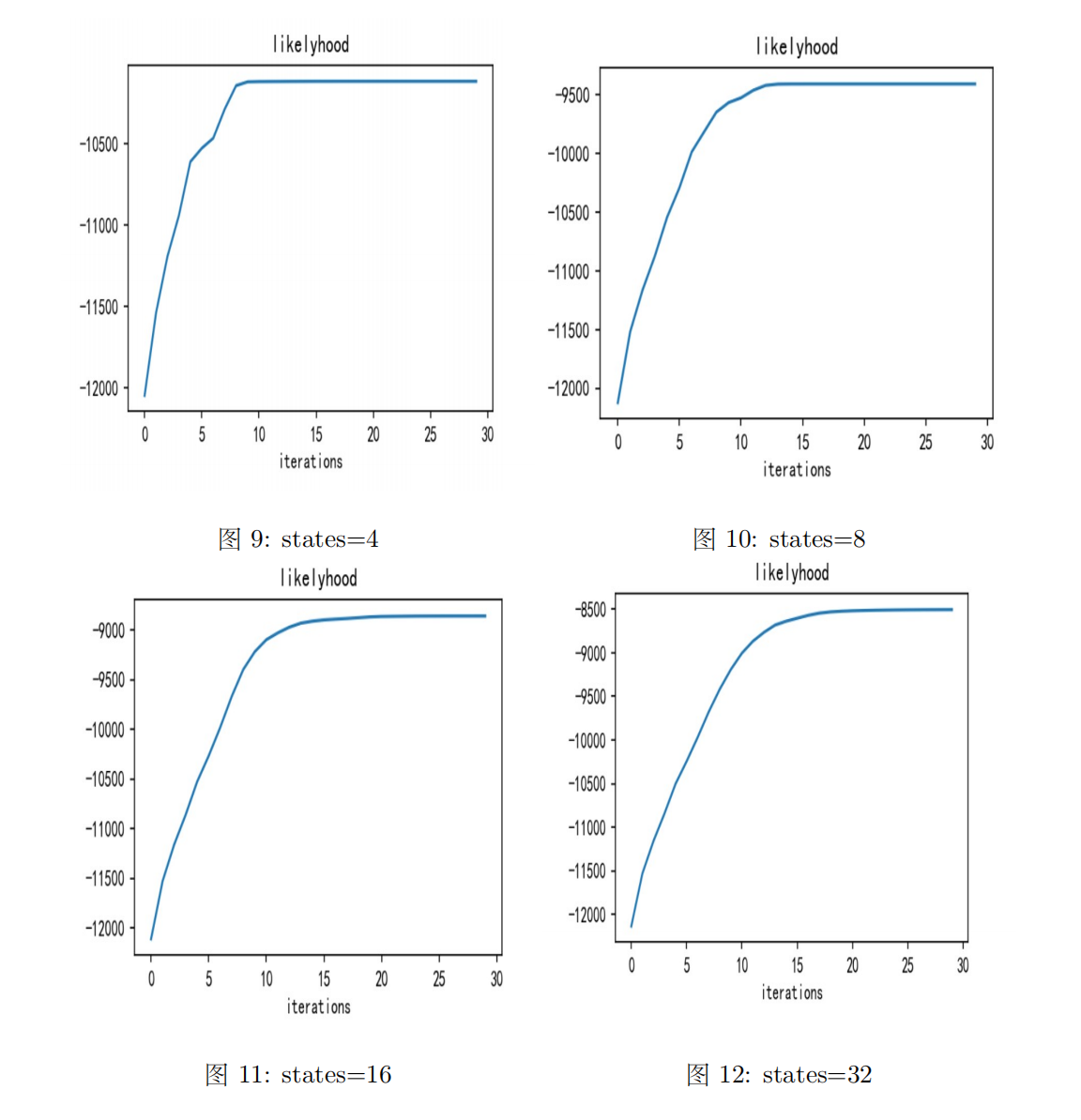
我们可以看到随着迭代次数的增加,对数似然越来越大,说明模型拟合效果越来越好。并且隐状态数目越多,最终对数似然函数值也越大,说明隐状态越多,模型效果越好。
(3)不同states下的股票指数拟合效果
不同states下的股票指数拟合效果如下图所示:
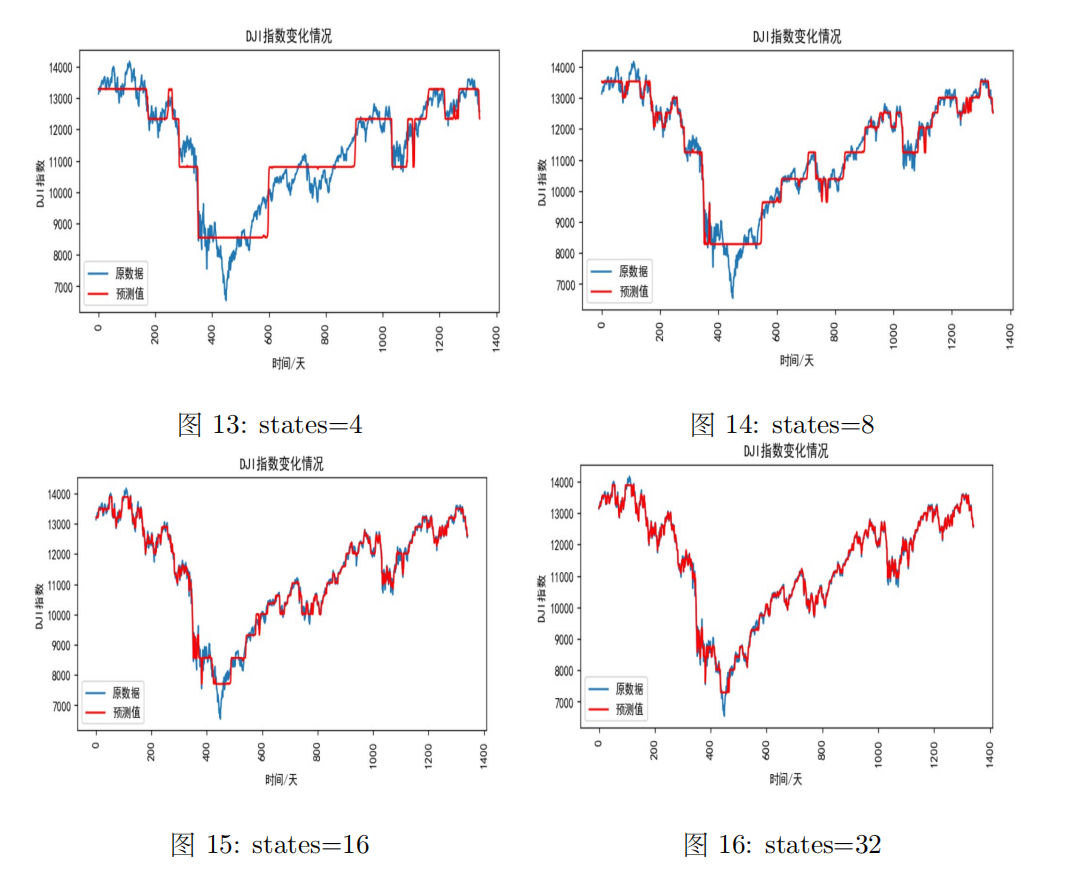
由上面不同隐状态下模型拟合效果图可知,states数越多,模型拟合效果越好,但是需要根据BIC和AIC准则以及训练模型的代价以及是否过拟合等方面来进行模型选择。
(4)不同states下的误差及MSE
不同states下的误差及MSE如下图所示:
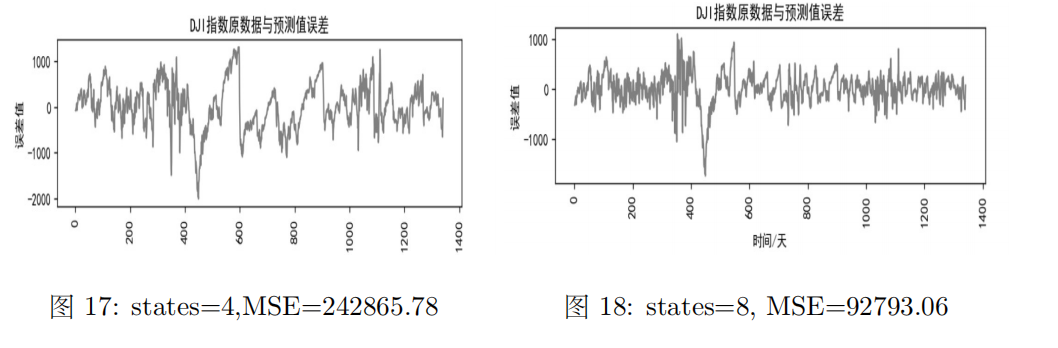
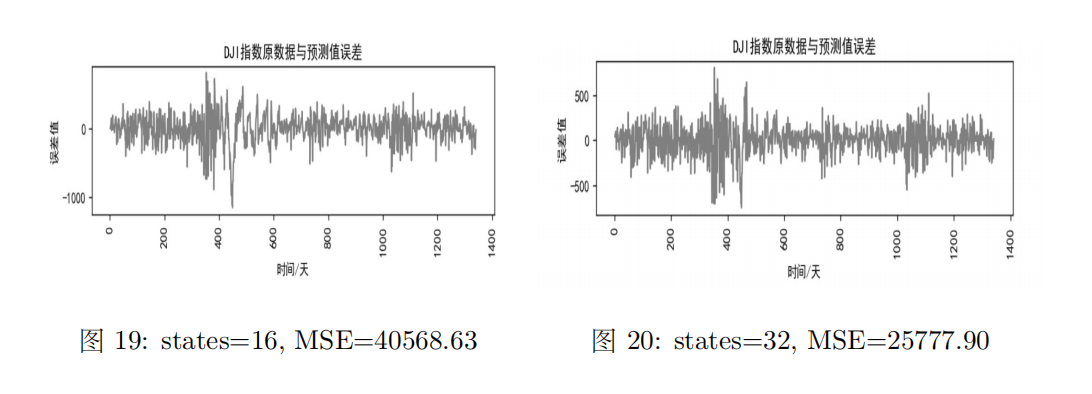
观察图中数据可知,states数越多,绝对误差与MSE越小,说明拟合效果越好。
(5)HMM模型单支股票预测小结
以DJI指数的收盘价为观测序列,隐状态数量states分别设为4,8,16,32,我们得到了不同情况下的HMM模型,并比较了训练所消耗时间,训练结果的AIC、BIC预测结果的平均误差、均方误差,结果如下表所示:
| States | Train Times | AIC | BIC | Mean Error | MSE |
|---|---|---|---|---|---|
| 4 | 25.84 sec | 20237.65 | 20258.46 | 384.13 | 242865.78 |
| 8 | 46.93 sec | 18827.66 | 18869.28 | 217.18 | 92793.06 |
| 16 | 78.43 sec | 17752.77 | 17836.00 | 145.24 | 40568.63 |
| 32 | 147.48 sec | 17074.84 | 17241.30 | 114.51 | 25777.90 |
我们可以看到随着隐状态数的增加:
- 模型的拟合误差不断减小
- AIC和BIC指数不断上升
- 对数似然也越来越大
- 但是模型训练时间也成倍上升
所以在实际应用的过程中,我们需要考虑模型越复杂带来提升的效果和代价,并且在两者之间找到一个权衡,而在后面的对比分析中,我们便采用的是隐状态数=16。(关于AIC和BIC的介绍可以看我这篇文章——时间序列分析入门:概念、模型与应用【ARMA、ARIMA模型】。
(6)多支股票训练模型
在前面的分析中,我们是对单只股票或者股票指数进行HMM建模,但事实上可以利用HMM对多只股票进行建模,这时多只股票共用同一个HMM参数和隐状态序列,我们以AAPL单支股票训练HMM模型得到如下结果:

可以看到单只股票建模相对误差率为3.1%,我们以AAPL与BAC、AAPL与C为例训练模型,得到的预测效果如下图所示:
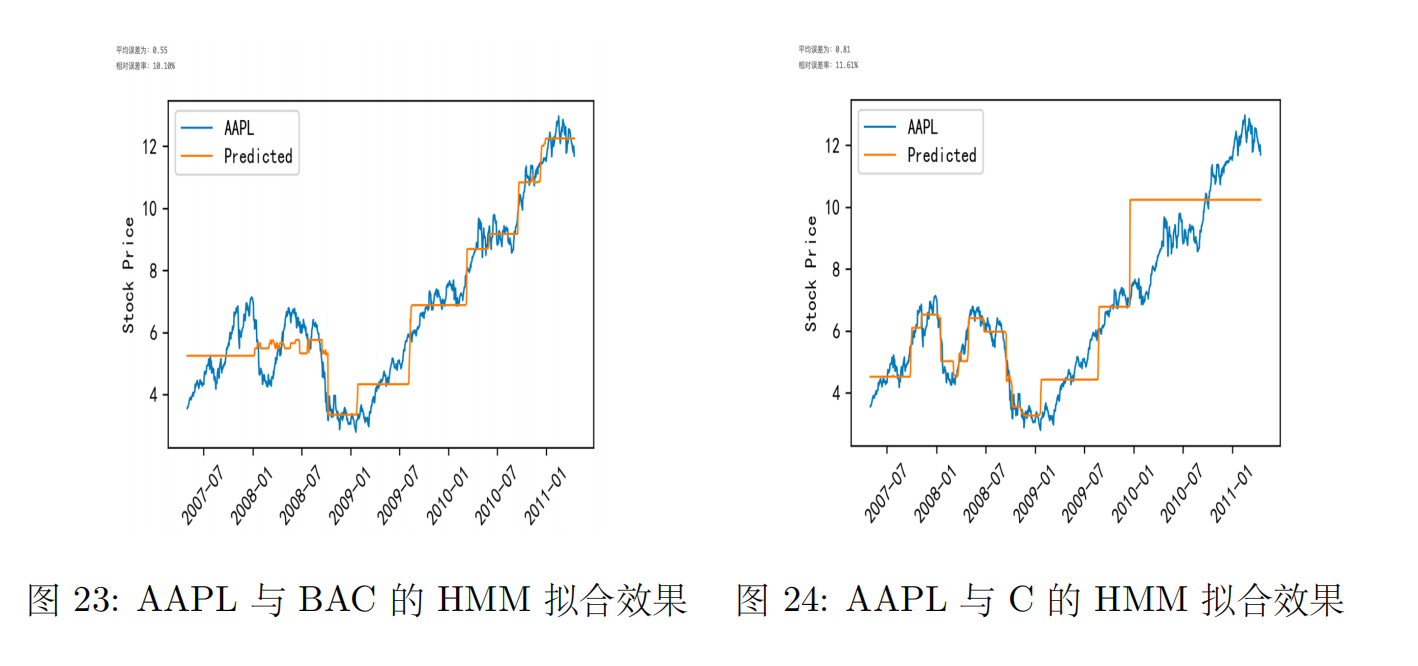
观察上两图知,多支股票数据训练出来的模型效果不如单支股票的效果,且由相关性分析知,相关性越大的两支股票组成的数据训练出的模型有更好的预测效果。不过这里面的原因可能比较复杂,有可能有负迁移的影响,不相关的股票数据导致共同建模效果反而不好。
相关文章:

基于隐马尔可夫模型的股票预测【HMM】
基于机器学习方法的股票预测系列文章目录 一、基于强化学习DQN的股票预测【股票交易】 二、基于CNN的股票预测方法【卷积神经网络】 三、基于隐马尔可夫模型的股票预测【HMM】 文章目录 基于机器学习方法的股票预测系列文章目录一、HMM模型简介(1)前向后…...

PostgreSQL Replication Slots
一、PostgreSQL的网络测试 安装PostgreSQL客户端 sudo yum install postgresql 进行网络测试主要是验证客户端是否能够连接到远程的PostgreSQL服务器。以下是使用psql命令进行网络测试的基本步骤: 连接到数据库: 使用psql命令连接到远程的PostgreSQL数据库服务器…...

centos7搭建zookeeper 集群 1主2从
centos7搭建zookeeper 集群 准备前提规划防火墙开始搭建集群192.168.83.144上传安装包添加环境变量修改zookeeper 的配置 192.168.83.145 和 192.168.83.146 配置 启动 集群 准备 vm 虚拟机centos7系统zookeeper 安装包FinalShell或者其他shell工具 前提 虚拟机安装好3台cen…...

Arrays.asList 和 java.util.ArrayList 区别
理解 Java 中的 Arrays.asList 和 java.util.ArrayList 的区别 在 Java 编程中,Arrays.asList 方法和 java.util.ArrayList 是两种常用的处理列表数据的方式。虽然它们在功能上看起来相似,但在内部实现和使用上有着本质的不同。本文将探讨这两种方式的区…...
代码随想录-Day44
322. 零钱兑换 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数…...
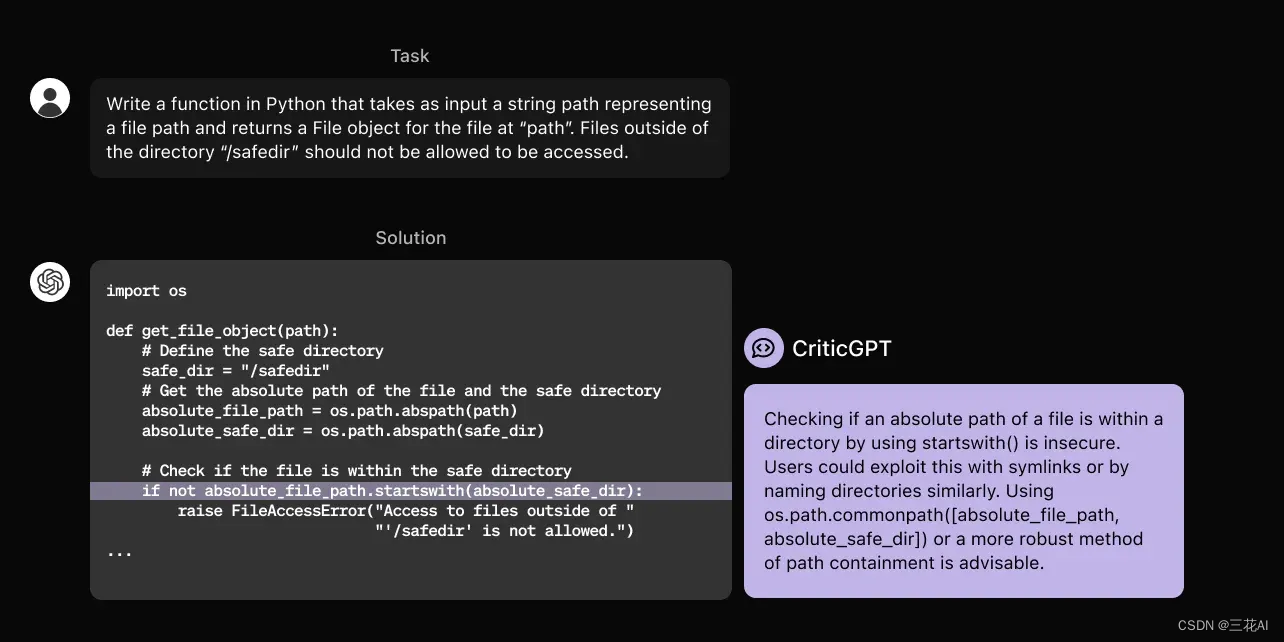
CriticGPT: 用 GPT-4 找出 GPT-4 的错误
CriticGPT 是 OpenAI 发布的一个基于 GPT-4 的模型,它可以帮助我们人类 Review 并纠正 ChatGPT 在生成代码时的错误。使用 CriticGPT 审查代码时,有 60% 的概率生成的代码更好更正确。...

SpringBoot:SpringBoot中调用失败如何重试
一、引言 在实际的应用中,我们经常需要调用第三方API来获取数据或执行某些操作。然而,由于网络不稳定、第三方服务异常等原因,API调用可能会失败。为了提高系统的稳定性和可靠性,我们通常会考虑实现重试机制。 Spring Retry为Spri…...

2024-06-24 问AI: 在大语言模型中,什么是ray?
文心一言 在大语言模型中,Ray是一个开源的统一框架,用于扩展AI和Python应用程序,特别是在机器学习领域。以下是关于Ray的详细解释: 核心功能: Ray为并行处理提供了计算层,使得用户无需成为分布式系统专家…...

仓库管理系统09--修改用户密码
1、添加窗体 2、窗体布局控件 UI设计这块还是传统的表格布局,采用5行2列 3、创建viewmodel 4、前台UI绑定viewmodel 这里要注意属性绑定和命令绑定及命令绑定时传递的参数 <Window x:Class"West.StoreMgr.Windows.EditPasswordWindow"xmlns"http…...

在Spring Data JPA中使用@Query注解
目录 前言示例简单示例只查询部分字段,映射到一个实体类中只查询部分字段时,也可以使用List<Object[]>接收返回值再复杂一些 前言 在以往写过几篇spring data jpa相关的文章,分别是 Spring Data JPA 使用JpaSpecificationExecutor实现…...
【UE5.1】Chaos物理系统基础——01 创建可被破坏的物体
目录 步骤 一、通过笔刷创建静态网格体 二、破裂静态网格体 三、“统一” 多层级破裂 四、“簇” 群集化的破裂 五、几何体集的材质 六、防止几何体集自动破碎 步骤 一、通过笔刷创建静态网格体 1. 可以在Quixel Bridge中下载两个纹理,用于表示石块的内外纹…...

Linux下SUID提权学习 - 从原理到使用
目录 1. 文件权限介绍1.1 suid权限1.2 sgid权限1.3 sticky权限 2. SUID权限3. 设置SUID权限4. SUID提权原理5. SUID提权步骤6. 常用指令的提权方法6.1 nmap6.2 find6.3 vim6.4 bash6.5 less6.6 more6.7 其他命令的提权方法 1. 文件权限介绍 linux的文件有普通权限和特殊权限&a…...

Redis主从复制搭建一主多从
1、创建/myredis文件夹 2、复制redis.conf配置文件到新建的文件夹中 3、配置一主两从,创建三个配置文件 ----redis6379.conf ----redis6380.conf ----redis6381.conf 4、在三个配置文件写入内容 redis6379.conf里面的内容 include /myredis/redis.conf pidfile /va…...
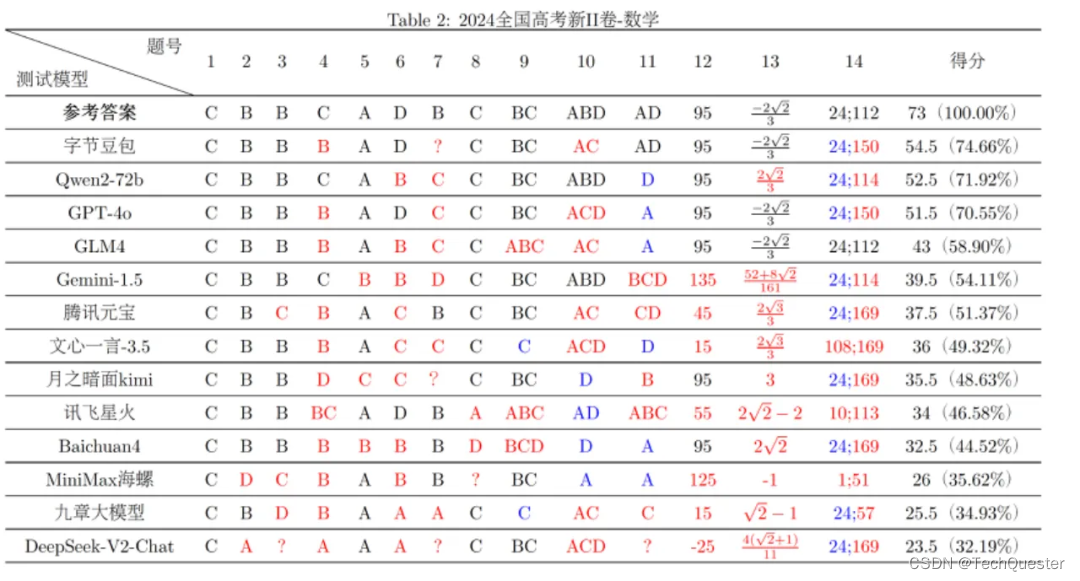
GPT-4o文科成绩超一本线,理科为何表现不佳?
目录 01 评测榜单 02 实际效果 什么?许多大模型的文科成绩竟然超过了一本线,还是在竞争激烈的河南省? 没错,最近有一项大模型“高考大摸底”评测引起了广泛关注。 河南高考文科今年的一本线是521分,根据这项评测&…...

Lombok的hashCode方法
Lombok对于重写hashCode的算法真的是很经典,但是目前而言有一个令人难以注意到的细节。在继承关系中,父类的hashCode针对父类的所有属性进行运算,而子类的hashCode却只是针对子类才有的属性进行运算,立此贴提醒自己。 目前重写ha…...

关于springboot创建kafkaTopic
工具类提供,方法名见名知意。使用kafka admin import org.apache.kafka.clients.admin.*; import org.apache.kafka.common.KafkaFuture;import java.util.*; import java.util.concurrent.ExecutionException;import org.apache.kafka.clients.admin.AdminClient; …...

OOAD的概念
面向对象分析与设计(OOAD, Object-Oriented Analysis and Design)是一种软件开发方法,它利用面向对象的概念和技术来分析和设计软件系统。OOAD 主要关注对象、类以及它们之间的关系,通过抽象、封装、继承和多态等面向对象的基本原…...

Day47
Day47 手写Spring-MVC之DispatcherServlet DispatcherServlet的思路: 前端传来URI,在TypeContainer容器类中通过uri得到对应的类描述类对象(注意:在监听器封装类描述类对象的时候,是针对于每一个URI进行封装的&#x…...

【面试系列】后端开发工程师 高频面试题及详细解答
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、…...

mac|浏览器链接不上服务器但可以登微信
千万千万千万不要没有关梯子直接关机,不然就会这样子呜呜呜 设置-网络,点击三个点--选择--位置--编辑位置(默认是自动) 新增一个,然后选中点击完成 这样就可以正常上网了...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
