每日一题——Python实现PAT乙级1096 大美数(举一反三+思想解读+逐步优化)3千字好文

一个认为一切根源都是“自己不够强”的INTJ
![]() 个人主页:用哲学编程-CSDN博客
个人主页:用哲学编程-CSDN博客![]() 专栏:每日一题——举一反三
专栏:每日一题——举一反三
Python编程学习
Python内置函数
Python-3.12.0文档解读
目录
我的写法
时间复杂度分析
空间复杂度分析
总结
哲学和编程思想
1. 抽象与具体化
2. 迭代与递归
3. 分治法
4. 组合数学
5. 优化与效率
6. 模块化与复用
7. 防御性编程
8. 算法复杂度
9. 简洁与清晰
10. 面向对象与函数式编程
总结
举一反三
1. 抽象与模块化
2. 迭代与递归
3. 分治法
4. 组合数学
5. 优化与效率
6. 模块化与复用
7. 防御性编程
8. 算法复杂度
9. 简洁与清晰
10. 面向对象与函数式编程
总结
题目链接:https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=1478633632938655744&page=0
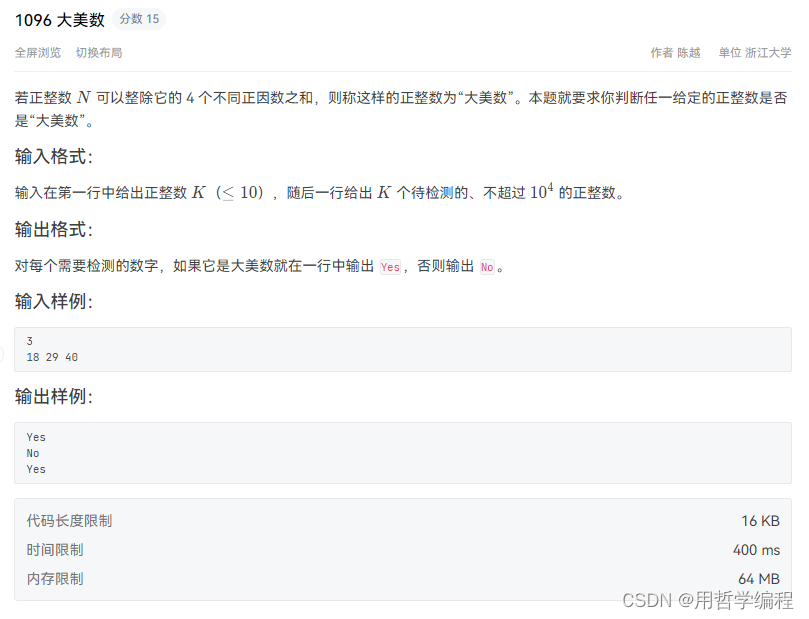
我的写法
import itertools
import mathdef factors(num):# 因数包括1和本身output = set()for i in range(1, int(math.sqrt(num)) + 1):if num % i == 0:output.add(i)output.add(num // i)return outputK = int(input())
nums = list(map(int, input().split()))for num in nums:num_factors = factors(num)#print(num_factors)if len(num_factors) >= 4:for combination in itertools.combinations(num_factors, 4):# 正整数 N 可以整除它的 4 个不同正因数之和,分清谁是除数被除数if sum(combination) %num == 0:#print(combination)print("Yes")breakelse:print("No")else:print("No")
时间复杂度分析
- 因数计算函数 factors(num):
- 该函数的时间复杂度主要由遍历从1到 sqrt(num) 的整数决定,因此是 O(sqrt(num))。
- 主程序逻辑:
- 对于每个正整数 num,计算因数的时间复杂度是 O(sqrt(num))。
- 如果因数集合的长度大于等于4,则需要生成所有可能的4个因数的组合,并检查每个组合的和是否能被 num 整除。
- 生成所有4个因数的组合的时间复杂度是 O(C_n^4),其中 n 是因数的数量。由于 n 通常远小于 num,这个复杂度可以近似为 O(n^4)。
- 因此,对于每个正整数 num,总的时间复杂度是 O(sqrt(num) + n^4)。
空间复杂度分析
- 因数计算函数 factors(num):
- 该函数使用了一个集合来存储因数,因此空间复杂度是 O(sqrt(num))。
- 主程序逻辑:
- 主程序逻辑的空间复杂度主要由存储因数集合 num_factors 决定,因此是 O(sqrt(num))。
- 此外,生成组合时会占用一些额外的空间,但由于组合的数量通常不会太大,这部分空间复杂度可以忽略不计。
总结
- 时间复杂度:对于每个正整数 num,总的时间复杂度是 O(sqrt(num) + n^4)。
- 空间复杂度:总的空间复杂度是 O(sqrt(num))。
这段代码在处理每个正整数时,能够有效地计算因数并检查是否存在满足条件的组合。然而,对于非常大的正整数,生成所有可能的4个因数的组合可能会导致较高的计算成本。
哲学和编程思想
这段代码体现了以下哲学和编程思想:
1. 抽象与具体化
- 抽象:代码通过定义函数 factors(num) 来抽象出计算一个数的所有因数的过程。这种抽象使得代码更模块化,便于理解和维护。
- 具体化:在主程序中,通过调用 factors(num) 函数并结合具体逻辑(如组合生成和条件判断)来解决具体问题。
2. 迭代与递归
- 迭代:代码中使用 for 循环来遍历因数和组合,这是一种迭代思想。迭代通常比递归更直观且效率更高。
3. 分治法
- 分治法:代码通过将问题分解为两个子问题:计算因数和检查组合。这种分治法使得问题更易于管理和解决。
4. 组合数学
- 组合数学:代码使用 itertools.combinations 来生成所有可能的4个因数的组合。这体现了组合数学中的组合生成思想。
5. 优化与效率
- 优化:代码在生成组合时,一旦找到满足条件的组合就立即返回结果,避免了不必要的计算,这是一种优化思想。
- 效率:通过使用集合 set 来存储因数,避免了重复因数,提高了效率。
6. 模块化与复用
- 模块化:代码通过定义独立的函数 factors(num),使得计算因数的过程可以被复用,体现了模块化编程思想。
- 复用:主程序中多次调用 factors(num) 函数,体现了代码复用的原则。
7. 防御性编程
- 防御性编程:代码在检查因数数量时,先判断因数数量是否大于等于4,这是一种防御性编程思想,确保程序在处理边界情况时不会出错。
8. 算法复杂度
- 算法复杂度:代码在计算因数时,通过遍历到 sqrt(num) 来减少计算量,体现了对算法复杂度的考虑。
9. 简洁与清晰
- 简洁:代码通过使用 itertools.combinations 和集合操作,使得代码简洁且易于理解。
- 清晰:代码结构清晰,逻辑明确,易于阅读和维护。
10. 面向对象与函数式编程
- 函数式编程:代码主要采用函数式编程风格,通过定义函数和使用高阶函数(如 itertools.combinations)来解决问题。
- 面向对象:虽然代码主要采用函数式编程风格,但也可以通过将函数封装到类中来实现面向对象编程。
总结
这段代码体现了抽象与具体化、迭代与递归、分治法、组合数学、优化与效率、模块化与复用、防御性编程、算法复杂度、简洁与清晰以及函数式编程等多种哲学和编程思想。这些思想共同构成了代码的设计和实现基础。
举一反三
根据上述哲学和编程思想,以下是一些技巧,可以帮助你举一反三,更好地解决类似问题:
1. 抽象与模块化
- 抽象化问题:将复杂问题分解为更小的、可管理的部分。例如,将计算因数的功能抽象为一个独立的函数。
- 模块化设计:确保每个函数或模块只做一件事,并且做得好。这样可以使代码更易于测试、维护和复用。
2. 迭代与递归
- 选择合适的循环结构:根据问题的性质选择使用 for 循环或 while 循环。通常,已知迭代次数时使用 for 循环,未知次数时使用 while 循环。
- 递归思维:对于可以自然分解为更小子问题的问题,考虑使用递归。但要注意递归的深度和效率。
3. 分治法
- 分解问题:将大问题分解为多个小问题,分别解决每个小问题,然后将结果合并。这有助于简化复杂问题的解决过程。
4. 组合数学
- 利用组合工具:使用 itertools 库中的组合生成工具(如 combinations 和 permutations)来处理需要生成组合或排列的问题。
5. 优化与效率
- 提前终止:在找到满足条件的解后立即返回,避免不必要的计算。
- 选择合适的数据结构:根据问题的需求选择合适的数据结构,如使用集合 set 来避免重复元素。
6. 模块化与复用
- 代码复用:设计可复用的函数和模块,避免重复代码。
- 库的使用:利用现有的库和工具,如 math 和 itertools,来提高开发效率。
7. 防御性编程
- 边界检查:在处理输入数据时,进行必要的边界检查,确保程序在异常情况下也能正常运行。
- 错误处理:使用异常处理机制来捕获和处理可能的错误。
8. 算法复杂度
- 选择合适的算法:根据问题的规模和性质选择合适的算法,考虑时间复杂度和空间复杂度。
- 优化算法:对算法进行优化,减少不必要的计算和存储。
9. 简洁与清晰
- 代码风格:保持代码风格一致,使用有意义的变量名和函数名,使代码易于理解。
- 注释和文档:添加必要的注释和文档,帮助他人理解代码。
10. 面向对象与函数式编程
- 选择编程范式:根据问题的性质选择合适的编程范式。函数式编程适合处理数据转换和计算密集型任务,而面向对象编程适合处理复杂的数据结构和对象交互。
- 混合使用:在必要时,可以将函数式编程和面向对象编程结合起来,发挥各自的优势。
总结
通过运用这些技巧,可以更好地理解和解决类似问题,提高编程能力和代码质量。不断实践和总结经验,将有助于在编程道路上不断进步。
相关文章:

每日一题——Python实现PAT乙级1096 大美数(举一反三+思想解读+逐步优化)3千字好文
一个认为一切根源都是“自己不够强”的INTJ 个人主页:用哲学编程-CSDN博客专栏:每日一题——举一反三Python编程学习Python内置函数 Python-3.12.0文档解读 目录 我的写法 时间复杂度分析 空间复杂度分析 总结 哲学和编程思想 1. 抽象与具体化 …...

无锁编程——从CPU缓存一致性讲到内存模型(1)
一.前言 1.什么是有锁编程,什么是无锁编程? 在编程中,特别是在并发编程的上下文中,“无锁”和“有锁”是描述线程同步和资源访问控制的两种不同策略。有锁(Locked): 有锁编程是指使用锁(例如互…...
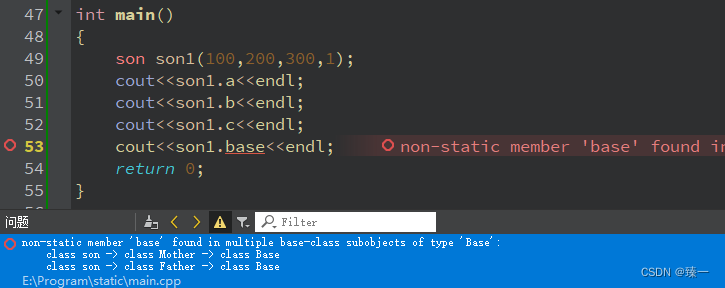
C++编程(七)继承
文章目录 一、继承(一)概念(二)语法格式(三)通过子类访问父类中的成员1. 类内2. 类外 (四)继承中的特殊成员函数1. 构造函数2. 析构函数3. 拷贝构造函数4. 拷贝赋值函数 二、多重继承…...

【ACM_2023】3D Gaussian Splatting for Real-Time Radiance Field Rendering
【ACM_2023】3D Gaussian Splatting for Real-Time Radiance Field Rendering 一、前言Abstract1 INTRODUCTION2 RELATED WORK2.1 Traditional Scene Reconstruction and Rendering2.2 Neural Rendering and Radiance Fields2.3 Point-Based Rendering and Radiance Fields 3 O…...
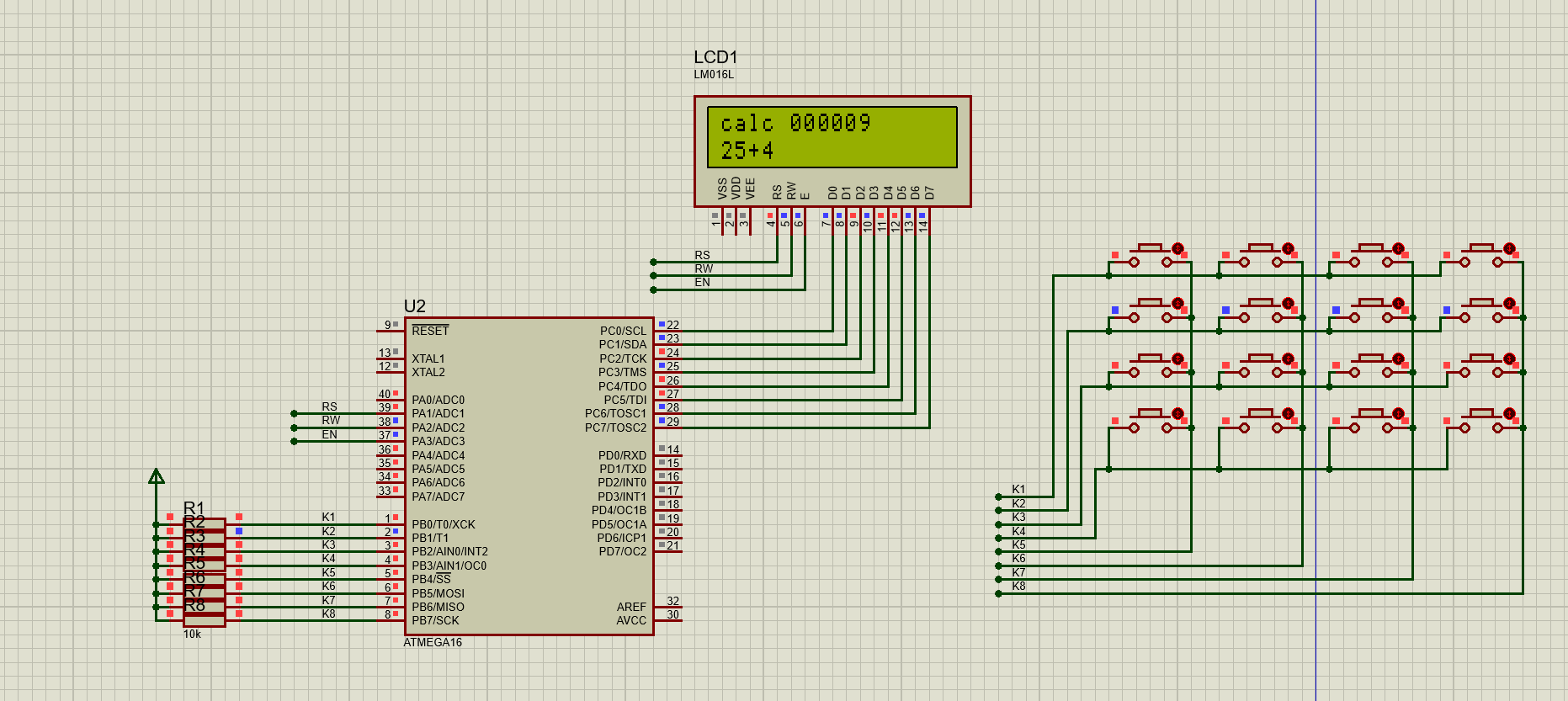
【TB作品】atmega16 计算器,ATMEGA16单片机,Proteus仿真
实验报告:基于ATmega16单片机的简易计算器设计 1. 实验背景 计算器是日常生活和工作中不可或缺的工具,通过按键输入即可实现基本的四则运算。通过本实验,我们将利用ATmega16单片机、矩阵键盘和LCD1602显示屏,设计并实现一个简易…...
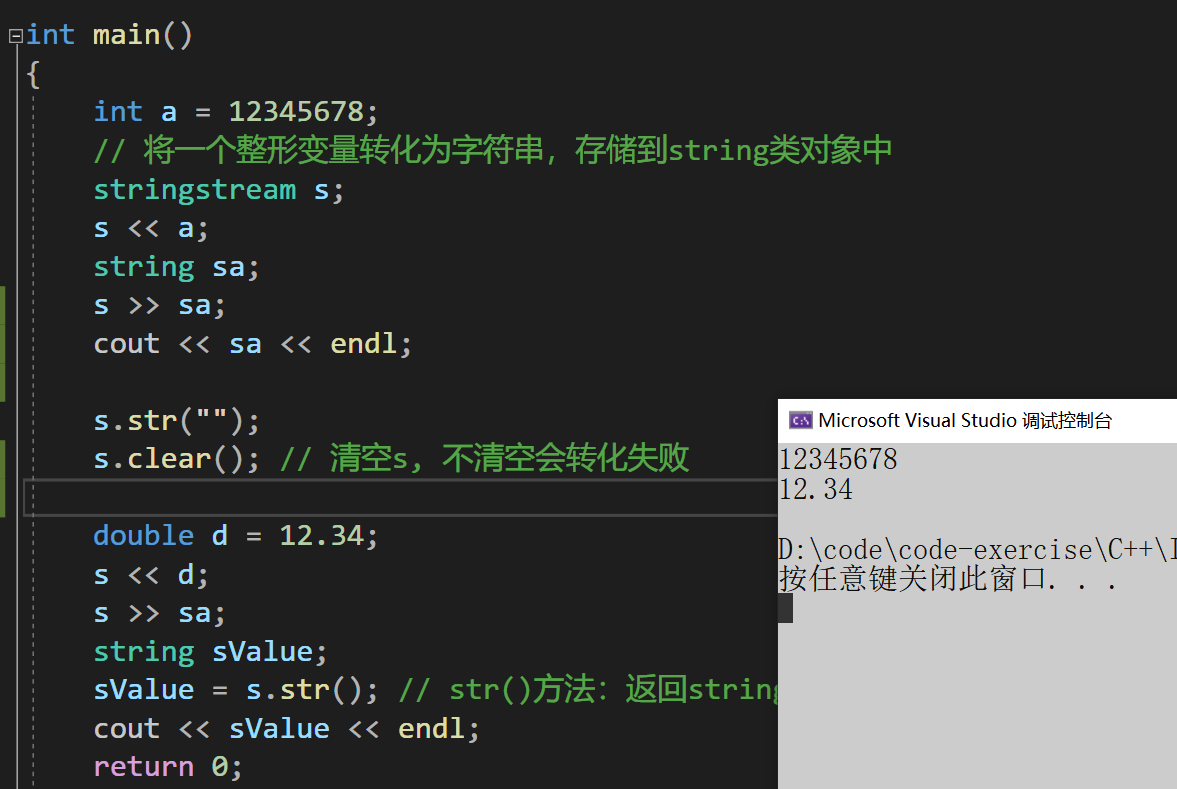
C++的IO流操作
文章目录 C语言的输入与输出流是什么CIO流C标准IO流C文件IO流二进制读写文本读写 stringstream的简单介绍 C语言的输入与输出 C语言的输入与输出 C语言中我们用到的最频繁的输入输出方式就是scanf()与printf()。 scanf(): 从标准输入设备(键盘)读取数据,并将值存放…...

MacOS升级指定Python版本的pip
场景: 系统默认是Python2.7,已经通过brew install python3.11 python3.12安装了多个版本的Python 执行:pip --version pip 24.1 from /Users/mac10.12/Library/Python/3.11/lib/python/site-packages/pip (python 3.11) 用的是Python3.11…...

音频Balance源码总结
音频Balance源码总结 何为音频Balance? 顾名思义,Balance及平衡,平衡也就是涉及多方,音频左右甚至四通道,调节所有通道的音量比,使用户在空间内听到各个通道的音频大小不一,好似置身于真实环境…...
- 需要自定义着色器)
CesiumJS【Basic】- #043 绘制脉冲线(Entity方式)- 需要自定义着色器
文章目录 绘制脉冲线(Entity方式)- 需要自定义着色器1 目标2 代码2.1 main.ts3 资源文件绘制脉冲线(Entity方式)- 需要自定义着色器 1 目标 使用Entity方式绘制脉冲线 2 代码 2.1 main.ts import * as Cesium from cesium;const viewer = new Cesium.Viewer(cesiumCont…...

Linux命令 wc(word count)-l(lines)用于统计文件中的行数。
文章目录 1、wc -l2、实战3、wc --help 1、wc -l 在命令 wc -l 中,-l 的英文全称是 lines。这个选项用于指定 wc(word count,单词计数)命令来统计文件的行数。 例如,当你运行 wc -l load_user_100w_sort.sql 时&…...

数据结构 - C/C++ - 链表
目录 结构特性 内存布局 结构样式 结构拓展 单链表 结构定义 节点关联 插入节点 删除节点 常见操作 双链表 环链表 结构容器 结构设计 结构特性 线性结构的存储方式 顺序存储 - 数组 链式存储 - 链表 线性结构的链式存储是通过任意的存储单元来存储线性…...
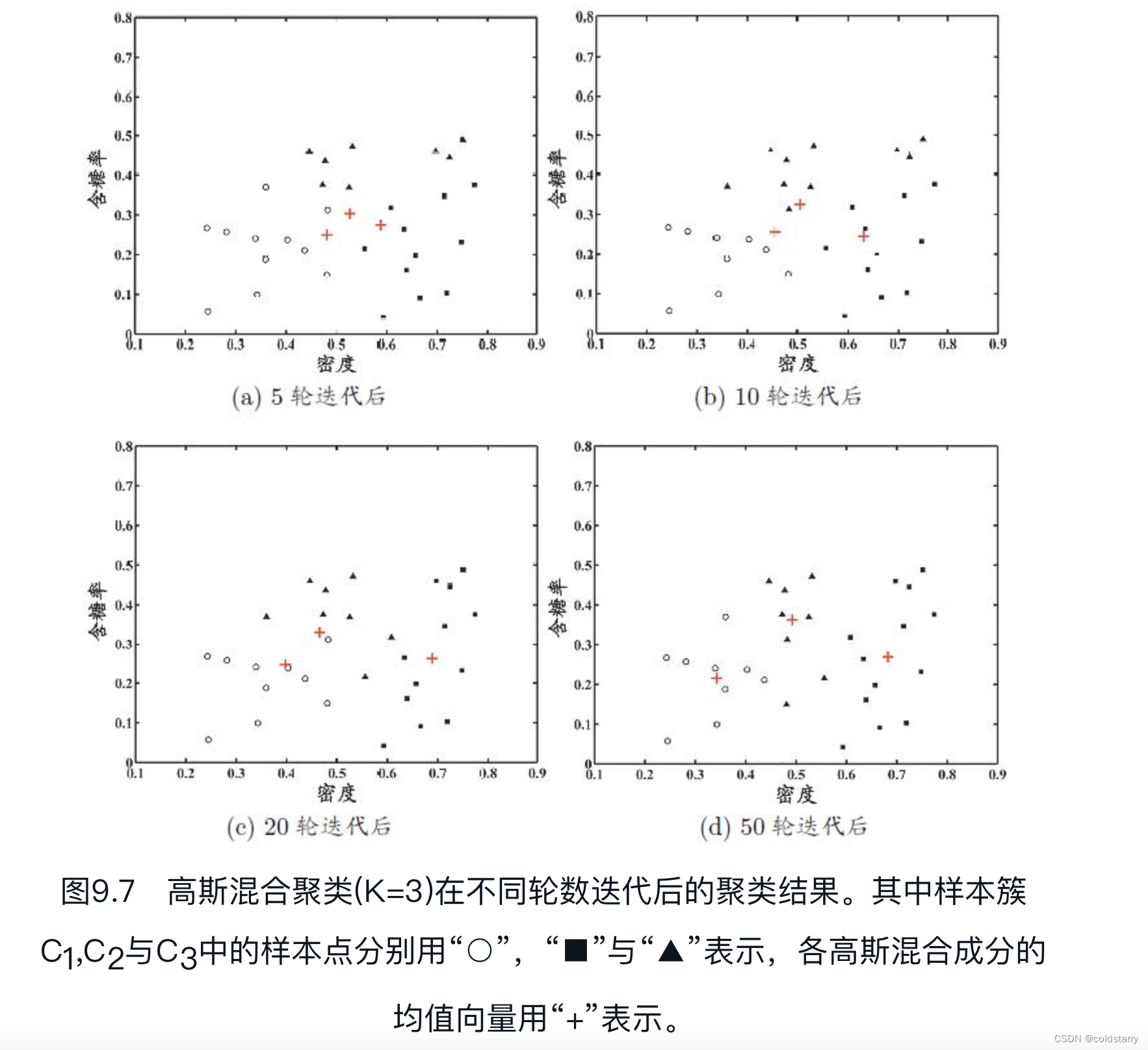
sheng的学习笔记-AI-高斯混合模型(GMM)
AI目录:sheng的学习笔记-AI目录-CSDN博客 需要学习前置知识: 聚类,可参考 sheng的学习笔记-AI-聚类(Clustering)-CSDN博客 EM算法,可参考 sheng的学习笔记-AI-EM算法-CSDN博客 贝叶斯,可参考 sheng的学习笔记-AI-…...
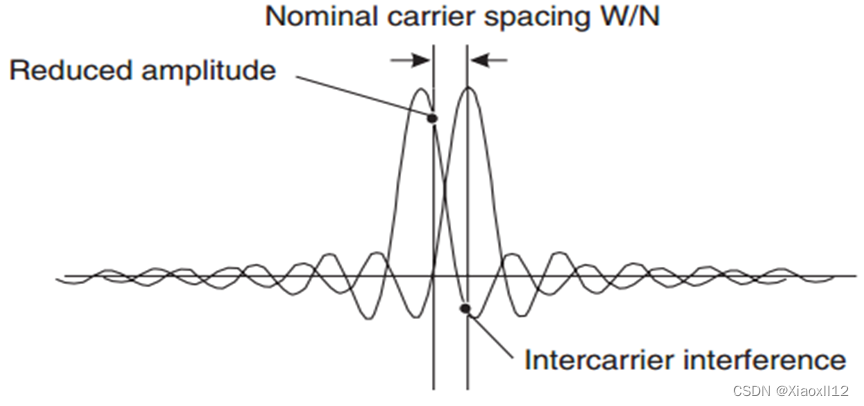
OFDM的缺点与关键技术
子载波间干扰英文简写ICI,ICI可能由各种原因引起 在多径信道中,CP小于最大附加时延时收发系统载波频率偏差和采样偏差收发系统相对移动,存在多普勒频移 ICI是制约OFDM系统性能的主要重要因素之一 对频率偏差敏感----->同步技术࿰…...
电脑录音软件哪个好?7款录制音频工具大盘点,赶快学起来!(2024)
也许你渴望提取你最喜欢的节目的背景音乐,或者你希望录制自己的声音制作教程。如果是这样,你就需要一款优秀的电脑录音软件,来帮助你捕捉任何你想要的声音,而且不会损失音质。目前市场上存在着大量的录制音频工具,面对…...

【Android面试八股文】你说你使用Leakcanary进行内存泄漏检测,那你能说一说Leakcanary的原理吗?
文章目录 一、 Java四大引用二、 LeakCanary示例工作机制注意事项三、 Leakcanary的原理四、 Leakcanary的源码分析LeakCanary#Install创建RefWatcherAndroidRefWatcherBuilder#buildAndInstall监听Activity的引用 : ActivityRefWatcher检查引用Dump Heap解析hprof定位泄露的引…...

蒂升电梯职业性格和Verify认知能力SHL测评答题攻略及薪资待遇解密!
一、蒂升电梯职业性格和认知能力测评考什么 您好!蒂升电梯公司邀请您参加的OPQ职业性格测评和Verify认知能力测评是两种常见的评估工具,用于帮助了解个人的职场性格特点和认知能力。 OPQ职业性格测评 这是一种性格测试,通常用于评估个人在…...
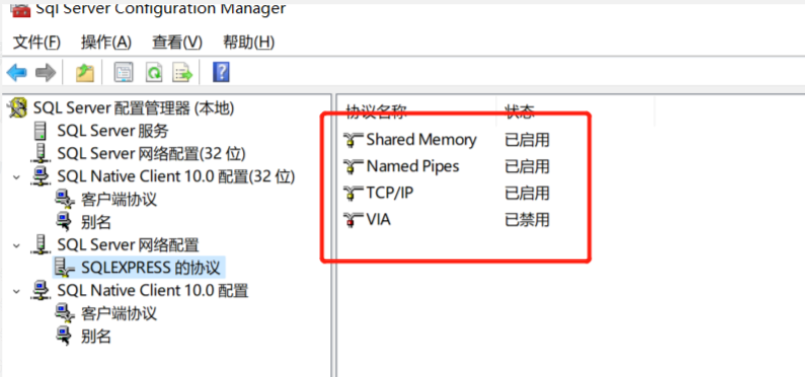
window上部署sql server改动端口、和sqlserver的一些还原、批量插入存储过程的命令
1.端口的查看和启动 --windows上安装上sql server数据库后,搜索界面搜索sql,会出现配置管理器,点击进入 --进入后再次选择配置管理器 2. sqlserver数据库还原图形化 sqlserver还原数据库时会使数据库进入一个restore的还原状态,…...
【单片机与嵌入式】stm32串口通信入门
一、串口通信/协议 (一)串口通信简介 串口通信是一种通过串行传输方式在电子设备之间进行数据交换的通信方式。它通常涉及两条线(一条用于发送数据,一条用于接收数据),适用于各种设备,从微控制…...

启动Redis服务器
名人说:一点浩然气,千里快哉风。 ——苏轼 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、在 Linux 或 macOS 上启动 Redis二、在 Windows 上启动 Redis三、配置 Redis 为服务启动&…...

uniapp中使用threejs加载几何体
我的建议是使用这个库 https://github.com/deepkolos/three-platformize 为什么?我试了uniapp推荐的和threejs-miniprogram这个小程序官方库,都加载不出来我的obj模型。所有我推荐不要用obj模型最好,挺多都支持GLTF模型的,但是我不…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
