队列_23约瑟夫问题+_24猫狗收容所
约瑟夫问题
n 个小孩围坐成一圈,并按顺时针编号为1,2,…,n,从编号为 p 的小孩顺时针依次报数,由1报到m ,当报到 m 时,该小孩从圈中出去,然后下一个再从1报数,当报到 m 时再出去。如此反复,直至所有的小孩都从圈中出去。请按出去的先后顺序输出小孩的编号。
Input
每行是用空格分开的三个整数,第一个是n,第二个是p,第三个是m (0 < m,n < 300)。最后一行是:
0 0 0
Output
按出圈的顺序输出编号,编号之间以逗号间隔。
Sample Input
8 3 4
0 0 0
Sample Output
6,2,7,4,3,5,1,8
#include<bits/stdc++.h>
using namespace std;
//队列
int main(){int n,p,m;while(cin>>n>>p>>m){queue<int> children;if(n==0 && p==0 && m==0){break;}for(int i=1;i<=n;i++){children.push(i);}for(int i=1;i<p;i++){children.push(children.front());children.pop();}while(!children.empty()){for(int j=1;j<m;j++){children.push(children.front());children.pop();}if(children.size()!=1){cout<<children.front()<<",";}else{cout<<children.front();}children.pop();}}return 0;
}
猫狗收容所
有家动物收容所只收留猫和狗,但有特殊的收养规则,收养人有两种收养方式:
第一种为直接收养所有动物中最早进入收容所的
第二种为选择收养的动物类型(猫或狗),并收养该种动物中最早进入收容所的。
给定一个操作序列代表所有事件。
若第一个元素为1,则代表有动物进入收容所,第二个元素为动物的编号,正数代表狗,负数代表猫;
若第一个元素为2,则代表有人收养动物,第二个元素若为0,则采取第一种收养方式,若为1,则指定收养狗,若为-1则指定收养猫。
请按顺序返回收养的序列。
若出现不合法的操作,即没有可以符合领养要求的动物,则将这次领养操作忽略。
输入:第一个是n,它代表操作序列的次数。接下来是n行,每行有两个值m和t,分别代表题目中操作的两个元素。
输出:按顺序输出收养动物的序列,编号之间以空格间隔。
#include<bits/stdc++.h>
using namespace std;
//队列
int main(){int n,m,t;//两个队列,一个是猫,一个是狗//如何得知最早进入收容所的动物//解决方法:三个队列:不现实,当猫或狗被领养的时候,总的队列没办法删除 //解决办法(新): queue<int> cat;queue<int> dog;int counter=0;cin>>n;while(n--){cin>>m>>t;if(m==1){if(t>0){counter++;dog.push(counter);dog.push(t);}else if(t<0){counter++;cat.push(counter);cat.push(t);}}else if(m==2){if(t==0){if(!dog.empty() && !cat.empty()){if(dog.front()<cat.front()){dog.pop();cout<<dog.front()<<" ";dog.pop();}else{cat.pop();cout<<cat.front()<<" ";cat.pop(); }}else if(!cat.empty() && dog.empty()){cat.pop();cout<<cat.front()<<" ";cat.pop(); }else if(cat.empty() && !dog.empty()){dog.pop();cout<<dog.front()<<" ";dog.pop(); }}else if(t==1){if(!dog.empty()){dog.pop();cout<<dog.front()<<" ";dog.pop(); }}else if(t==-1){if(!cat.empty()){cat.pop();cout<<cat.front()<<" ";cat.pop();}}}}return 0;
}
(本题也可以把counter与编号合起来使用结构体,需要注意一下队列为空时的几种情况)
相关文章:

队列_23约瑟夫问题+_24猫狗收容所
约瑟夫问题 n 个小孩围坐成一圈,并按顺时针编号为1,2,…,n,从编号为 p 的小孩顺时针依次报数,由1报到m ,当报到 m 时,该小孩从圈中出去,然后下一个再从1报数,当报到 m 时再出去。如此反复&#…...

gradle
Gradle环境介绍OpenJDK 17.0.5Gradle 7.6示例代码 fly-gradleGradle 项目下文件介绍如果你的电脑安装了 gradle,可以使用 gradle init 去初始化一个新的 gradle 工程,然后使用电脑安装的 gradle 去执行构建命令。但是每个开发电脑上的 gradle 版本不一样…...

[牛客]链表中倒数第k个结点
使用快慢指针法:两种思路:1.fast先向后走k-1次,slow再向后走1次,然后fast和slow同时向后走,当fast走到最后一个结点时,slow刚好在倒数第k个位置上;2.fast先向后走k次,slow再向后走1次,然后fast和slow同时向后走,当fast走到最后一个结点的后面时(此时为NULL),slow刚好在倒数第k个…...

English Learning - L2 语音作业打卡 双元音 [eɪ] [aɪ] Day14 2023.3.6 周一
English Learning - L2 语音作业打卡 双元音 [eɪ] [aɪ] Day14 2023.3.6 周一💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 /eɪ/…...

C++ this 指针与静态成员
文章目录参考描述实例成员与静态成员实例成员静态成员静态成员属性隐式形参 this 指针冲突this 指针静态成员函数this 指针与静态成员函数参考 项目精通C (第九版)托尼加迪斯、朱迪沃尔特斯、戈德弗雷穆甘达 (著) / 黄刚 等 &…...

REDIS16_LRU算法概述、查看默认内存、默认是如何删除数据、缓存淘汰策略
文章目录①. LRU算法概述②. 查看默认内存③. 如何删除数据④. 缓存淘汰策略①. LRU算法概述 ①. LRU是Least Recently Used的缩写,即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的数据给予淘汰 (leetcode-cn.com/problems/lru-cache) ②. LRU算法题来源 ③.…...
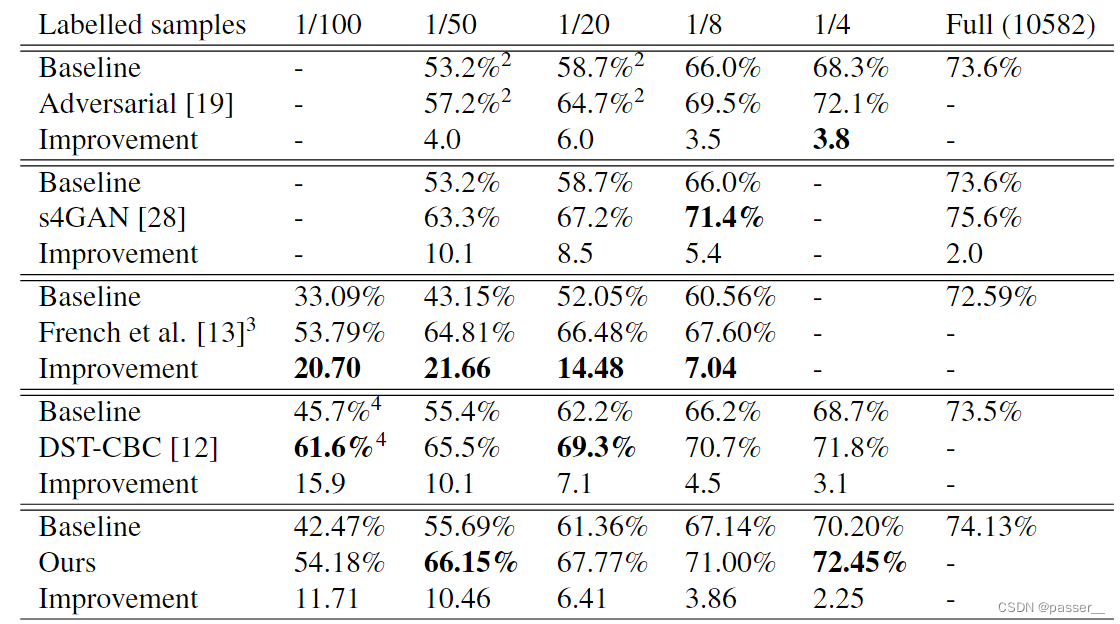
ClassMix: Segmentation-Based Data Augmentation for Semi-Supervised Learning学习笔记
ClassMix相关介绍主要思想方法Mean-Teacher损失函数交叉熵损失标签污染实验实验反思参考资料相关介绍 从DAFormer溯源到这篇文章,ClassMix主要是集合了伪标签和一致性正则化,思想来源于CutMix那条研究路线,但是优化了CutMix中的标签污染的情…...

CSDN竞赛第35期题解
CSDN竞赛第35期题解 1、题目名称:交换后的or 给定两组长度为n的二进制串,请问有多少种方法在第一个串中交换两个不同位置上的数字,使得这两个二进制串“或”的 结果发生改变? int n;cin>>n; string a,b;cin>>a>…...

Java应用服务系统安全性,签名和验签浅析
1 前言 随着互联网的普及,分布式服务部署越来越流行,服务之间通信的安全性也是越来越值得关注。这里,笔者把应用与服务之间通信时,进行的的安全性相关,加签与验签,进行了一个简单的记录。 2 安全性痛点 …...

spring中bean的实例化
构造方法实现实例化 无参构造器实例化 我们之前用的就一直是无参构造器实现实例化,虽然没有在类中写构造器,但是每个类都会有一个默认的无参构造器 有参构造器实例化 相比于无参构造器,我们只需要传入参数就可以了 我们可以通过construc…...
磨皮插件portraiture2023最新中文版
Portraiture滤镜是一款 Photoshop,Lightroom 和 Aperture 插件,DobeLighttroom 的 Portraiture 消除了选择性掩蔽和逐像素处理的繁琐的手工劳动,以帮助您在肖像修整方面取得卓越的效果。它是一个强大的,但用户友好的插件照明.这是…...

记录每日LeetCode 2269.找到一个数组的K美丽值 Java实现
题目描述: 一个整数 num 的 k 美丽值定义为 num 中符合以下条件的 子字符串 数目: 子字符串长度为 k 。 子字符串能整除 num 。 给你整数 num 和 k ,请你返回 num 的 k 美丽值。 注意: 允许有 前缀 0 。 0 不能整除任何…...

代码管理--svnadmin工具介绍
1、简介 SVNAdmin2 是一款通过图形界面管理服务端SVN的web程序。正常情况下配置SVN仓库的人员权限需要登录到服务器手动修改 authz 和 passwd 两个文件,当仓库结构和人员权限上了规模后,手动管理就变的非常容易出错,本系统能够识别人员和权限…...
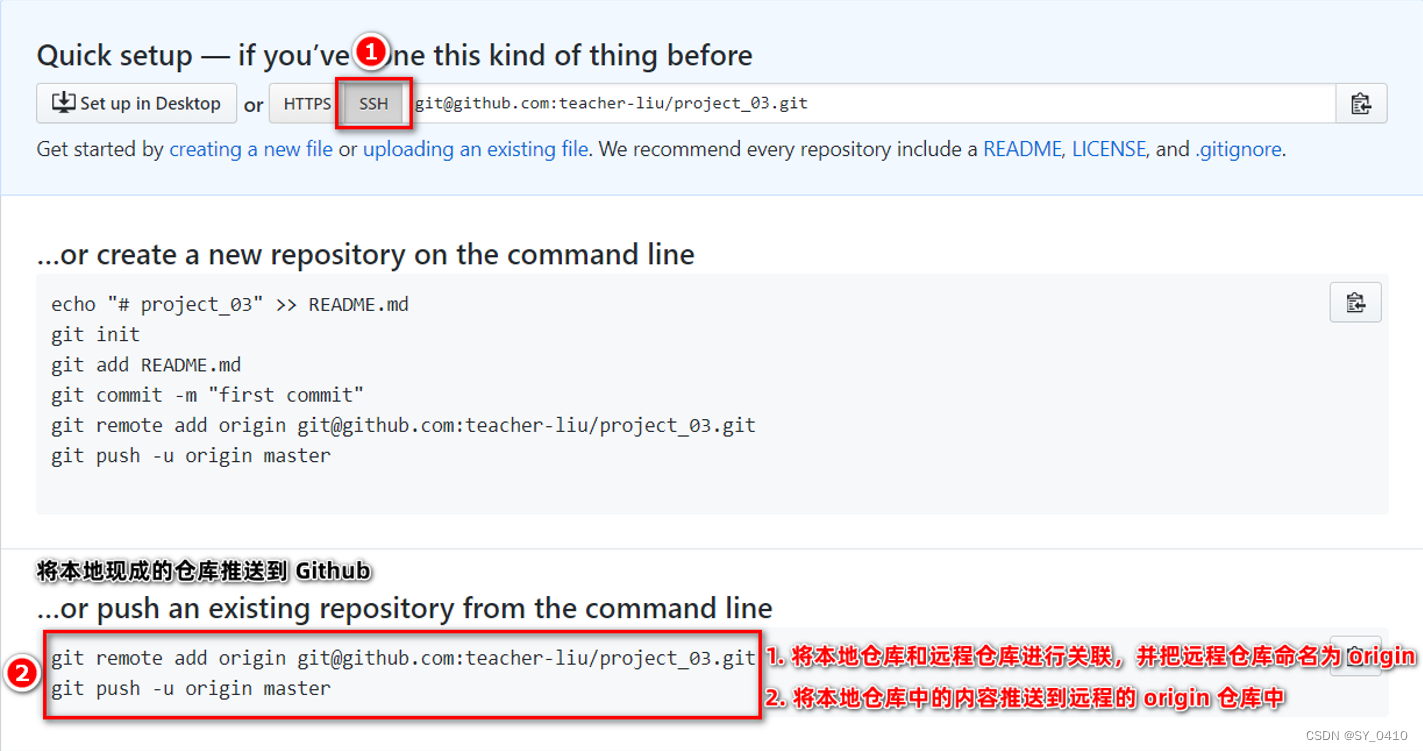
Git的基本使用以及上传到GitHub
GIT的基本使用一、安装并配置GIT二、Git的基本操作三、使用GIT上传至GitHub四、Git分支一、安装并配置GIT 1.安装GIT连接 GIT安装包链接 2.打开GIT 鼠标右键点击Git Bash Here 安装完 Git 之后,第一件事就是设置自己的用户名和邮件地址。因为通过 Git 对项目进行…...

国科大论文latex模板中可能的注意事项
背景 国科大2022年9月发布了毕业论文的LaTeX模板,它是在ucasthesis上修改而来的,但近日使用国科大发布版本时发现有几点不同以及需要注意的地方。本人只会简单使用latex,但并不熟悉latex样式编辑,因此以下介绍与方法仅供参考。仅…...
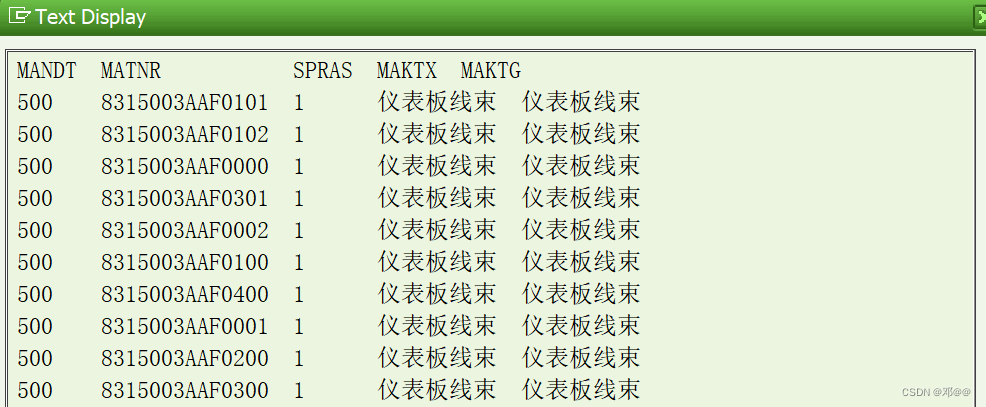
ABAP 怎样将XML和JSON格式转换为HTML格式显示
ABAP 怎样将XML和JSON格式转换为HTML格式显示 一、将JSON格式转换为HTML格式 BAP接口程序开发中时常会用到JSON格式来传输数据,在监控传输的JSON串内容时,把JSON转换为HTML格式来显示会很便利。下面提供一个简单例子来实现JSON转化为HTML并显示的功能。…...

基础课DP
DP 背包问题01背包问题完全背包问题多重背包问题多重背包问题II分组背包问题线性DP数字三角形最长上升子序列最长上升子序列II最长公共子序列编组距离区间DP石子合并计数类DP整数划分数位统计DP计数问题状态压缩DP蒙德里安的梦想最短Ha路径树形DP没有上司的舞会...

基于支持向量机SVM的风电场NWP数据预测,SVM的详细原理
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的风电场NWP预测 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定…...
webRtc概念
webRtc概念 以下的文档整理来自此链接 文档整理了一系列实现web通用接口的ECMAScript APIs ,这些接口是为了支持浏览器或者一些其他实现了实时交换协议的设备进行媒体信息和程序数据交换。 1、实现点对点通信的规范: NAT穿透实现与远端节点链接比如&a…...
数据结构与算法基础(王卓)(16):KMP算法详解(代码实现)
实现代码的过程中 具体细节、问题: (1):关于写Get_next函数的标题: 现象: PPT上写的是: void get_next(SString T, int &next[]) 然而并不能运行,而当我们去掉了引用符号&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
