机器学习(三)
机器学习
- 4.回归和聚类算法
- 4.1 线性回归
- 4.1.1 线性回归的原理
- 4.1.2 线性回归的损失和优化原理
- 4.2 欠拟合与过拟合
- 4.2.1 定义
- 4.2.2 原因以及解决方法
- 4.2.3 正则化
- 4.3 线性回归改进-岭回归
- 4.3.1 带L2正则化的线性回归-岭回归
- 4.3.2 API
- 4.4 分类算法-逻辑回归与二分类
- 4.4.1 定义
- 4.4.2 逻辑回归的应用场景
- 4.4.3 逻辑回归的原理
- 4.4.4 逻辑回归API
- 4.4.5模型评估
- 4.5 模型保存和加载
- 4.6 无监督学习 K-means算法
- 4.6.1 无监督学习包含算法
- 4.6.2 K-means原理
4.回归和聚类算法
4.1 线性回归
4.1.1 线性回归的原理
-
线性回归应用场景
- 房价预测
- 销售额度预测
- 贷款额度预测
-
什么是线性回归
-
定义与公式
-
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
-
特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归。
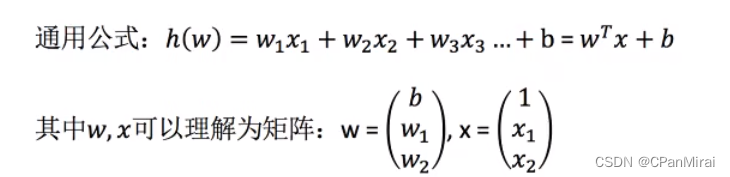
-
-
-
线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。
-
线性关系
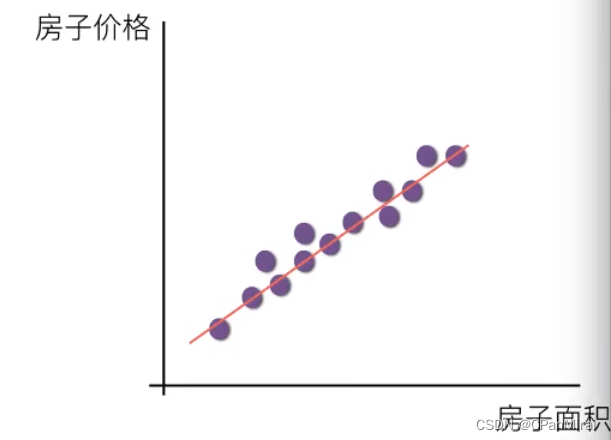
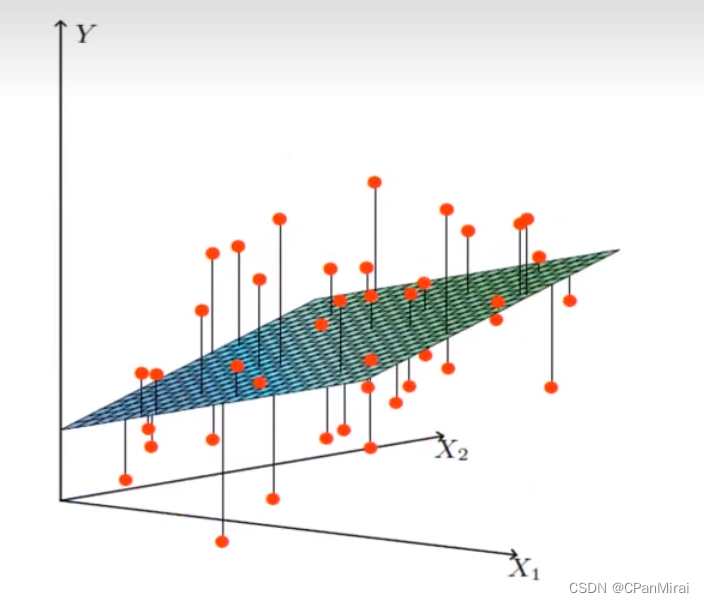
注:单特征与目标值的关系呈现直线关系,两个特征与目标值呈现平面的关系。
-
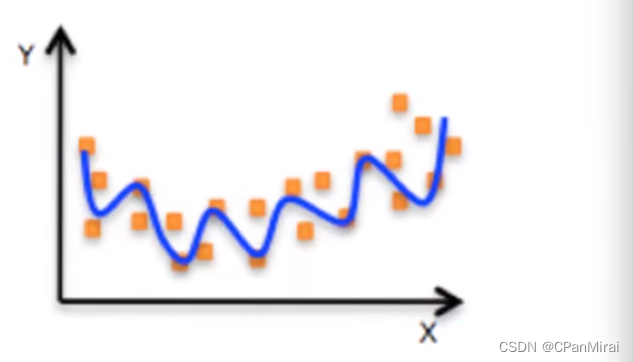
非线性关系(可以理解为 W1*X1 + W2X22+W3*X33+b)
-
-
4.1.2 线性回归的损失和优化原理
真实的线性关系和我们预测的线性关系存在一定误差,那么存在,我们需要把这个误差进行衡量出来(使用损失函数),我们想办法去减少误差,去修正(优化损失),不断地去逼近真实的线性关系,从而预测的结果更加准确。
-
损失函数(最小二乘法):

-
优化损失
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归中经常用两种优化算法:
-
正规方程(直接求解得到W,使用高数里面求最小值的方法,进行求导)

-
梯度下降(不断试错,最终找到合适的)
-
4.2 欠拟合与过拟合
4.2.1 定义
欠拟合:一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模拟过于简单)
过拟合:一个假设在训练数据上能够很好的拟合,但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
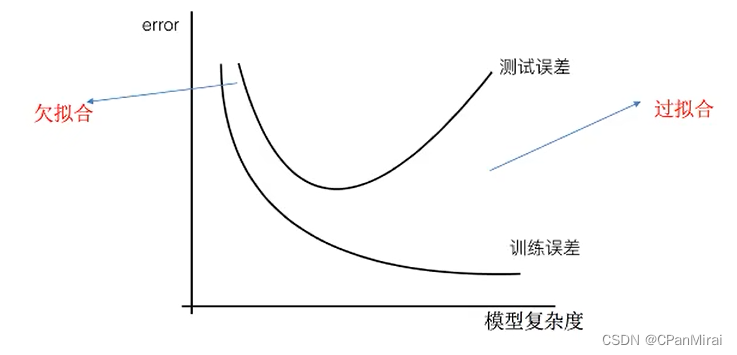
4.2.2 原因以及解决方法
- 欠拟合原因以及解决方法
- 原因:学习到数据的特征过少
- 解决方法:增加数据的特征数量
- 过拟合原因以及解决办法
- 原因:原始特征过多,存在一些嘈杂特征,模型过于复杂,因为模型尝试去兼顾各个测试数据点。
- 解决方法:正则化

如何解决 ?

4.2.3 正则化
-
L2 正则化
-
作用:可以使得其中一些W的都很小,都接近于0,削弱某个特征的影响。
-
优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。
-
加入L2正则化后的损失函数(Ridge回归):

-
-
L1正则化
- 作用:可以使得其中一些W的值直接为0,删除这个特征的影响。
- LASSO回归
4.3 线性回归改进-岭回归
4.3.1 带L2正则化的线性回归-岭回归
岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上正则化的限制,从而达到解决过拟合的效果。
4.3.2 API
# 具有L2正则化的线性回归
sklearn.linear_model.Ridge(alpha = 1.0,fit_intercept = True,solver = 'auto',normalize = False)# alpha : 正则化力度(惩罚项系数),也叫 λ# solver : 会根据数据自动选择优化方法 如果数据集、特征都比较大,选择该随机梯度下降优化# normalize : 数据是否进行标准化# normalize = False : 可以在fit之间调用preprocessing.StandardScaler标准化数据# Ridge.coef_ : 回归权重# Ridge.intercept_ : 回归偏置
Ridge方法相当于SGDRegressor(penalty = ‘L2’, loss = ‘squared_loss’),只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG)
从右往左,正则化程度越来越大,weights也就是惩罚项值接近于0.
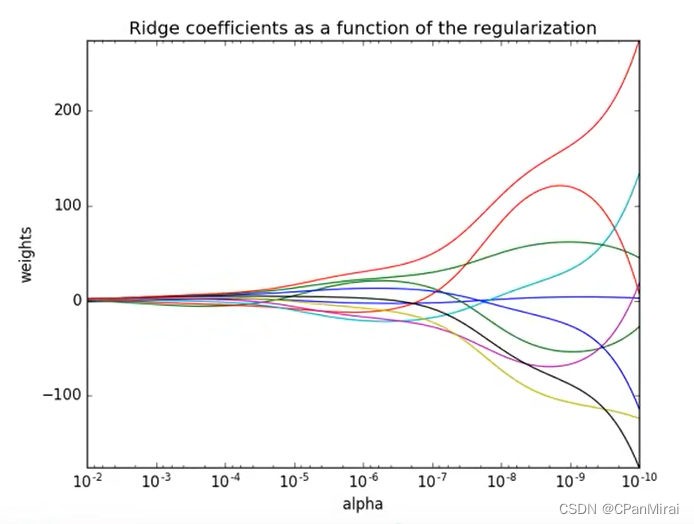
4.4 分类算法-逻辑回归与二分类
4.4.1 定义
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛。
4.4.2 逻辑回归的应用场景
- 广告点击率
- 是否为垃圾邮件
- 是否患病
- 金融诈骗
- 虚假账号
4.4.3 逻辑回归的原理
-
输入(是线性回归的结果)
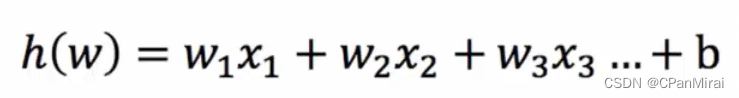
-
激活函数
-
sigmoid函数
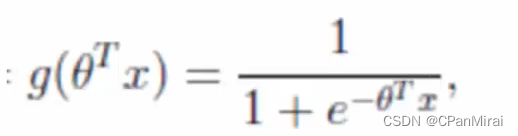
-
分析
- 回归的结果输入到sigmoid函数中去
- 输出结果:[0,1]区间中的一个概率值,默认为0.5为阈值
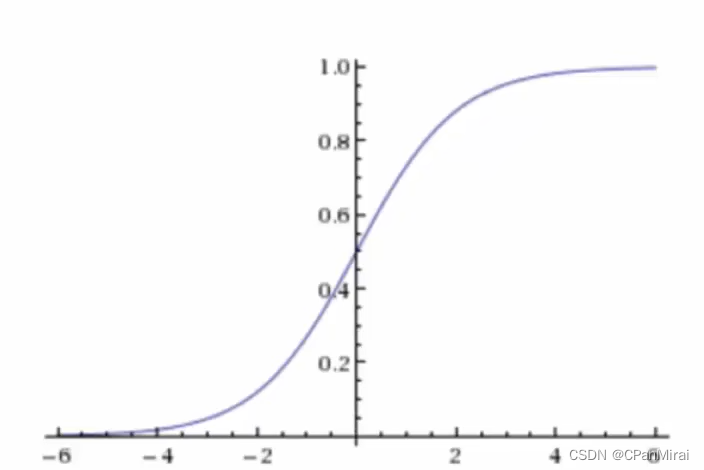
-
逻辑回归最终的分 类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外一个类别标记为0(反例)
-
损失以及优化
逻辑回归的损失,称之为对数似然损失,公式如下:
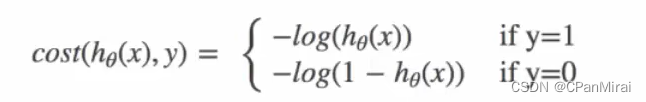
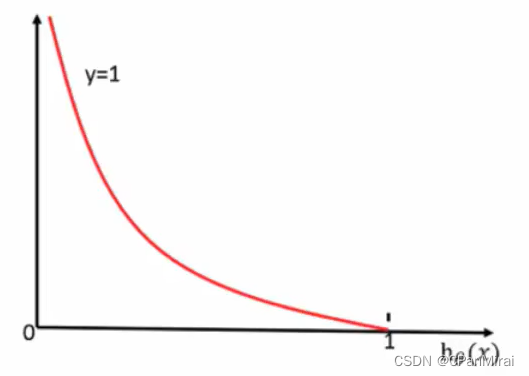
当 y = 1时:
当 y = 0时:
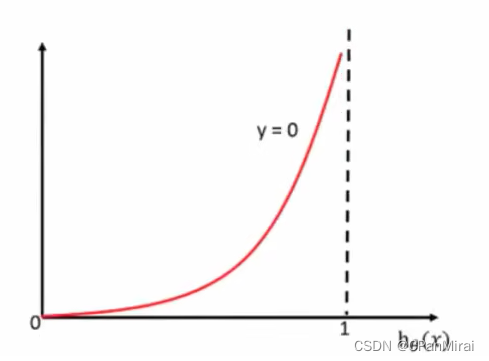
其中h(x)是预测值,y是真实值,坐标纵轴是损失值。h(x) = y 时无损失,否则损失趋于无穷。
-
综合完整损失函数
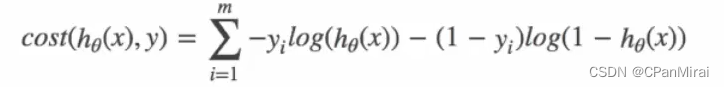
优化:同样使用梯度下降优化算法,去减少损失函数的值,这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率。
4.4.4 逻辑回归API
sklearn.linear_model.LogisticRegression(solver = 'liblinear',penalty = 'l2',C = 1.0)# solver : 优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)# penalty : 正则化的种类# C:正则化力度
LogisticRegression方法相当于SGDClassifier(loss = ‘log’,penalty=’ '),GDClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average=True。而使用LogisticRegression(实现了SAG)。
4.4.5模型评估
-
精确率和召回率
-
混淆矩阵
-
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)。
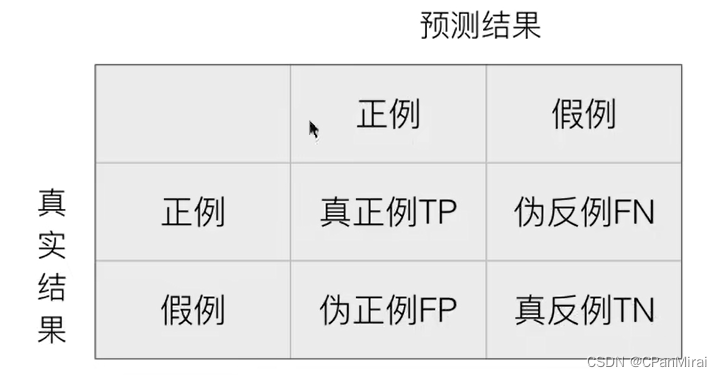
-
-
精确率和召回率
-
精确率:预测值为正例样本中真实为正例的比例。

-
召回率:真实为正例的样本中预测结果为正例的比例。
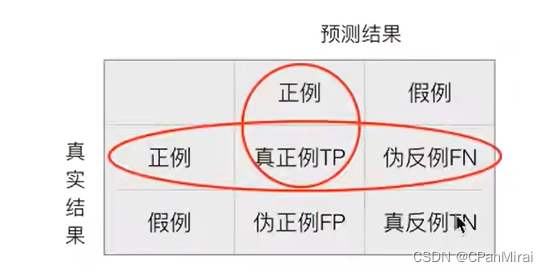
-
-
-
分类评估报告API
sklearn.metrics.classification_report(y_true,y_pred,labels=[],target_names=None)# y_true:真实值# y_pred:估计器预测目标值# labels:指定类别对应的数字# target_names:目标类别名称# return:每个类别精确率与召回率 -
ROC曲线与AUC指标(在样本不均衡下评估)
-
TPR(召回率)与FPR
- TPR = TP/(TP+FN) 所有真实类别为1的样本中,预测类别为1的比例。
- FPR = FP/(FP+TN) 所有真实类别为0的样本中,预测类别为1的比例。
-
ROC曲线
-
ROC曲线的横轴就是FPRate,纵轴就是TPRate,当二者相等时,表示的意义则是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的,此时AUC为0.5
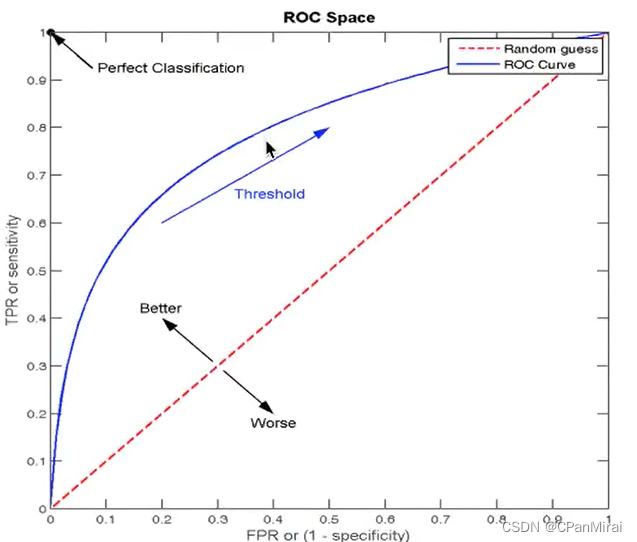
-
-
AUC指标
- AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率。
- AUC的最小值为0.5,最大值为1,取值越高越好。
- AUC=1,完美分类器,采用这个预测模型时,不管设定什么值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定值的话,能有预测
价值。
注:最终AUC的范围在[0.5,1]之间,并且越接近1越好。
-
AUC计算API
-
总结
- AUC只能用来评价二分类
- AUC非常适合样本不平衡中的分类器性能
from sklearn.metrics import roc_auc_score sklearn.metrics.roc auc_score(y_true,y_score) # 计算ROC曲线面积,即AUC值 # "y_true:每个样本的真实类别,必须为0(反例),1(正例)标记 # "y_score:预测得分,可以是正类的估计概率、置信值或者分类器方法的返回值
-
4.5 模型保存和加载
4.5.1 sklearn模型的保存和加载API
import joblib
# 保存:joblib.dump(rf,'test.pkl')
# 加载:estimator = joblib.load('test.pkl')
4.6 无监督学习 K-means算法
4.6.1 无监督学习包含算法
- 聚类
- K-means(k均值聚类)
- 降维
- PCA
4.6.2 K-means原理
-
效果图
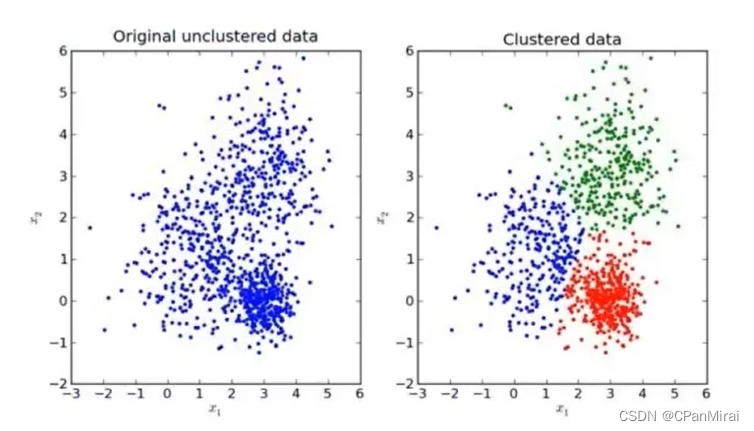
-
K-means聚类步骤
- 随机设置K个特征空间内的点作为初始的聚类中心
- 对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程
-
K-means API
sklearn.cluster.KMeans(n_clusters = 8,init = 'k-means++') # n_clusters:开始聚类中心的数量 # init:初始化方法,默认为'K-means++' # labels_:默认标记的类型,可以和真实值进行比较 -
Kmeans性能评估
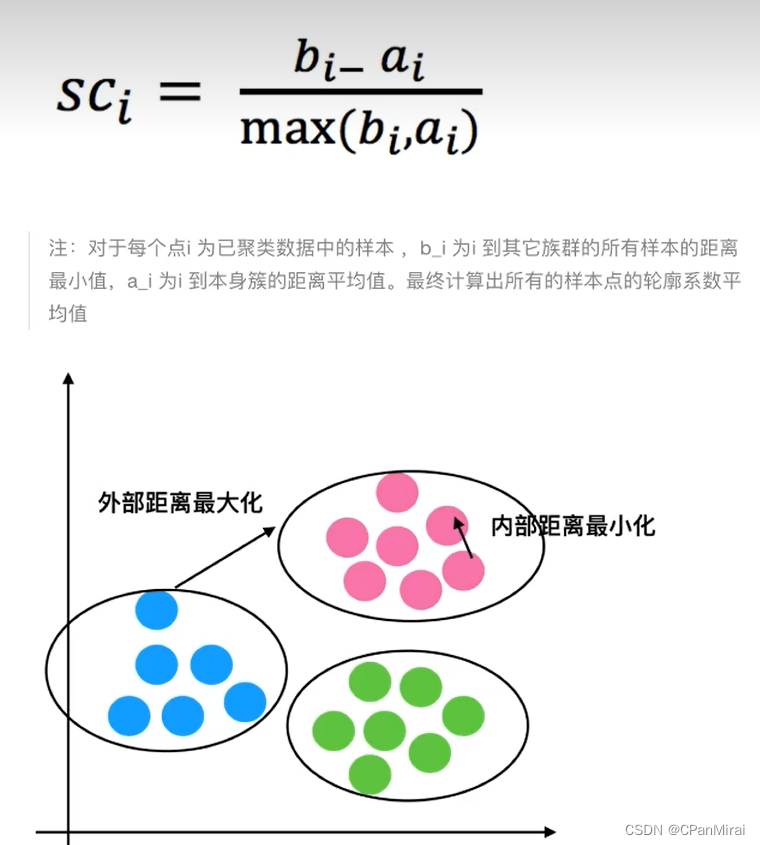
结论:如果b_i >> a_i趋近于1效果越好,b_i << a_i 趋近于 -1,效果不好。轮廓系数的值是介于[-1,1],越接近于1代表内聚度和分离度都相对较优。
-
轮廓系数API
sklearn.metrics.silhouette_score(X,labels) # 计算所有样本的平均值轮廓系数 # x : 特征值 # labels : 被聚类标记的目标值 -
K-means总结
- 特点:采用迭代式算法,直观易懂并且实用
- 缺点:容易收敛到局部最优解(可以用多次聚类解决)
相关文章:

机器学习(三)
机器学习 4.回归和聚类算法4.1 线性回归4.1.1 线性回归的原理4.1.2 线性回归的损失和优化原理 4.2 欠拟合与过拟合4.2.1 定义4.2.2 原因以及解决方法4.2.3 正则化 4.3 线性回归改进-岭回归4.3.1 带L2正则化的线性回归-岭回归4.3.2 API 4.4 分类算法-逻辑回归与二分类4.4.1 定义…...
)
PostgreSQL 基本SQL语法(二)
1. SELECT 语句 1.1 基本 SELECT 语法 SELECT 语句用于从数据库中检索数据。基本语法如下: SELECT column1, column2, ... FROM table_name; 例如,从 users 表中检索所有列的数据: SELECT * FROM users; 1.2 使用 WHERE 条件 WHERE 子…...

linux 控制台非常好用的 PS1 设置
直接上代码 IP$(/sbin/ifconfig eth0 | awk /inet / {print $2}) export PS1"\[\e[35m\]^o^\[\e[0m\]$ \[\e[31m\]\t\[\e[0m\] [\[\e[36m\]\w\[\e[0m\]] \[\e[32m\]\u\[\e[0m\]\[\e[33m\]\[\e[0m\]\[\e[34m\]\h(\[\e[31m\]$IP\[\e[m\])\[\e[0m\]\n\[\e[35m\].O.\[\e[0m\]…...
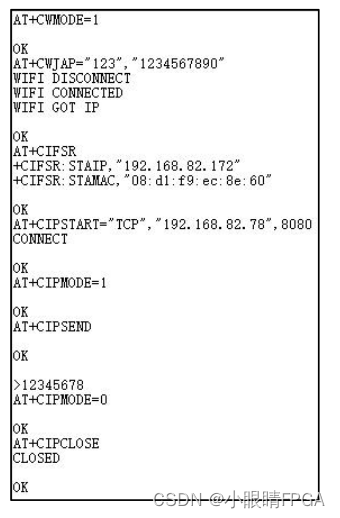
【紫光同创盘古PGX-Nano教程】——(盘古PGX-Nano开发板/PG2L50H_MBG324第十二章)Wifi透传实验例程说明
本原创教程由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处(www.meyesemi.com) 适用于板卡型号: 紫光同创PG2L50H_MBG324开发平台(盘古PGX-Nano) 一:…...

详述乙级资质企业在城市综合管廊与隧道一体化设计中的挑战与机遇
挑战 1. 技术与设计复杂性 城市综合管廊与隧道项目往往涉及复杂的地质条件、地下水位、周边建筑物影响等因素,要求企业具备高水平的岩土工程、结构工程和流体力学等专业知识。此外,一体化设计需要跨学科合作,协调不同系统的兼容性ÿ…...
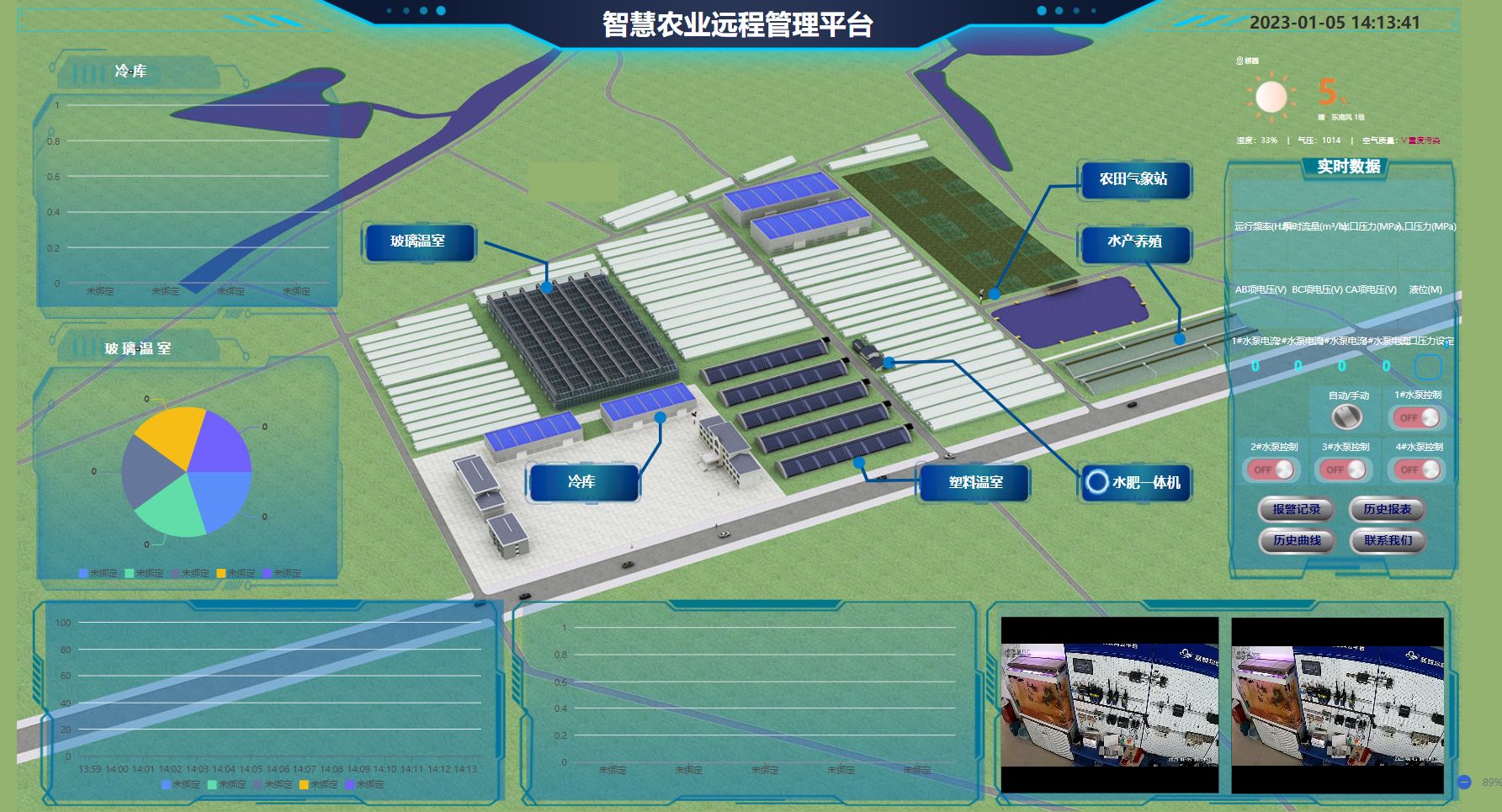
如何借助物联网实现农情监测与预警
如何借助物联网实现农情监测与预警? 物联网技术,作为信息技术与传统行业的深度融合产物,正逐步变革着农业生产的管理模式,特别是在农情监测与预警领域展现出巨大潜力。其核心在于通过感知层的各类传感器、通信层的数据传输技术以…...

一个项目学习Vue3---响应式基础
观察下面一段代码,学习响应式基础的全部内容 <template><div><div>将下面的msg属性放到上面来:{{ msg }}</div><button click"count">{{ count }}</button><button click"object.count.value">{{ o…...

白骑士的Python教学基础篇 1.5 数据结构
系列目录 上一篇:白骑士的Python教学基础篇 1.4 函数与模块 数据结构是编程语言中用于存储和组织数据的基本构件。在Python中,常见的数据结构包括列表(List)、元组(Tuple)、字典(…...

Go 常用文件操作
查找文件/目录 os.Stat(String)组合路径 dir, _ : homedir.Dir() filename : args[0] path : filepath.Join(dir, filename)homedir.Dir()为home根目录。 filepath.Join 会自动处理分隔符,将目录和文件名组合成文件路径。 检查是否含有后缀.json strings.HasSu…...

大数据、人工智能、云计算、物联网、区块链序言【大数据导论】
各位大佬好 ,这里是阿川的博客,祝您变得更强 个人主页:在线OJ的阿川 大佬的支持和鼓励,将是我成长路上最大的动力 阿川水平有限,如有错误,欢迎大佬指正 本篇序言前 必看 【大数据导论】—大数据序言 这是…...
ComfyUI流程图、文生图、图生图步骤教学!
前言 leetcode , 209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 …...

CSS基础知识学习指南
CSS基础知识学习指南 1. 介绍 CSS(层叠样式表)是用于描述HTML文档的呈现样式的语言。通过CSS,可以控制网页的布局、颜色、字体等各种样式,使得网页更加美观和用户友好。 2. CSS基础语法 CSS由选择器和声明块组成。选择器用于选…...

力扣hot100 -- 贪心算法
👂 ▶ 逍遥叹 - 胡歌&沈以城【Mashup】 (163.com) 👂 庐州月 - 许嵩 - 单曲 - 网易云音乐 2.7 小时,加上写博客,4 道题,😂 -- 希望二刷时,可以 3 小时,8 道题.... 目录 &…...

P2P文件传输协议介绍
P2P文件传输协议是一种基于对等网络(Peer-to-Peer,简称P2P)的文件共享和传输技术。以下是关于P2P文件传输协议的详细介绍: 一、定义与原理 P2P文件传输协议允许网络中的各个节点(即计算机或其他设备)之间…...

Spring Boot集成Spring Mobile快速入门Demo
1.什么是Spring Mobile? Spring Mobile是一个基于Spring Web MVC框架扩展的一个针对不同移动终端的应用开发框架。通过它我们在适配不同终端方面,就不用费劲心思了。 Spring Mobile的主要功能 自动设备检测: Spring Mobile在 server端内置了一个设备解…...

走进开源企业 | 湖南大学OpenHarmony技术实训活动在开鸿智谷顺利举办!
6月24日-6月26日,2024开放原子校源行之湖南大学信息科学与工程学院师生走进开源企业实训交流活动顺利落下帷幕。湖南大学信息科学与工程学院的师生代表团一行90人参与了湖南开鸿智谷数字产业有限公司(以下简称“开鸿智谷”)与母公司拓维信息系…...
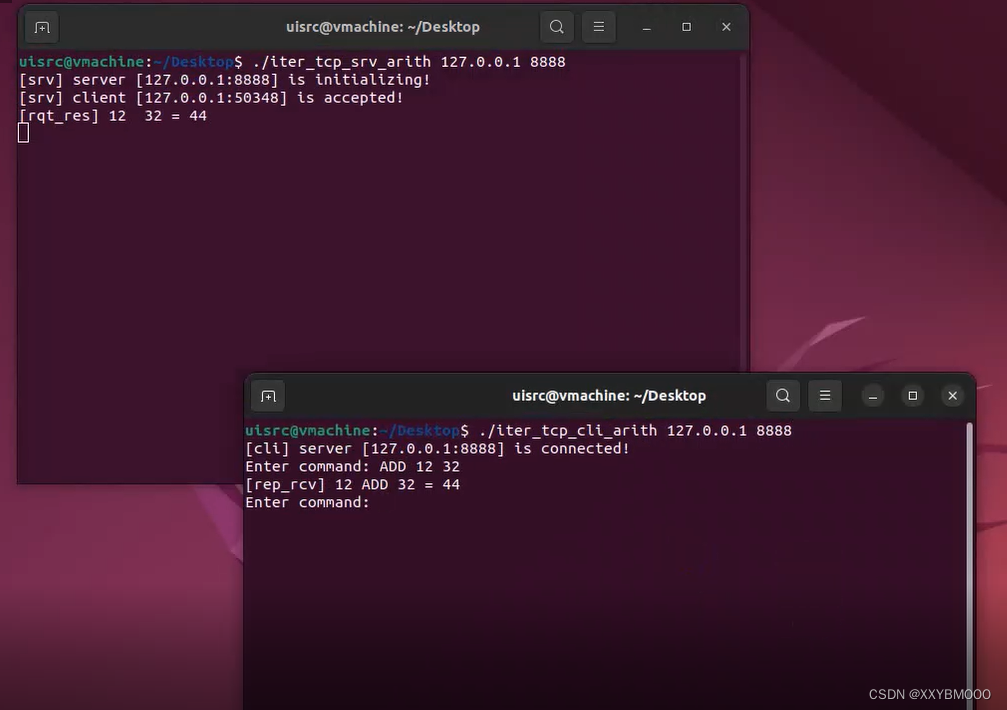
TCP单进程循环服务器程序与单进程客户端程序
实验目的 理解并掌握以下内容: 网络进程标识(即套接字地址)在Linux中的数据结构与地址转换函数。网络字节序与主机字节序的定义、转换以及相关函数在网络编程中的应用。数据结构内存对齐的基本规则,以及基于数据结构构建PDU的基本方法。TCP单进程循环服务器与单进程客户端的…...
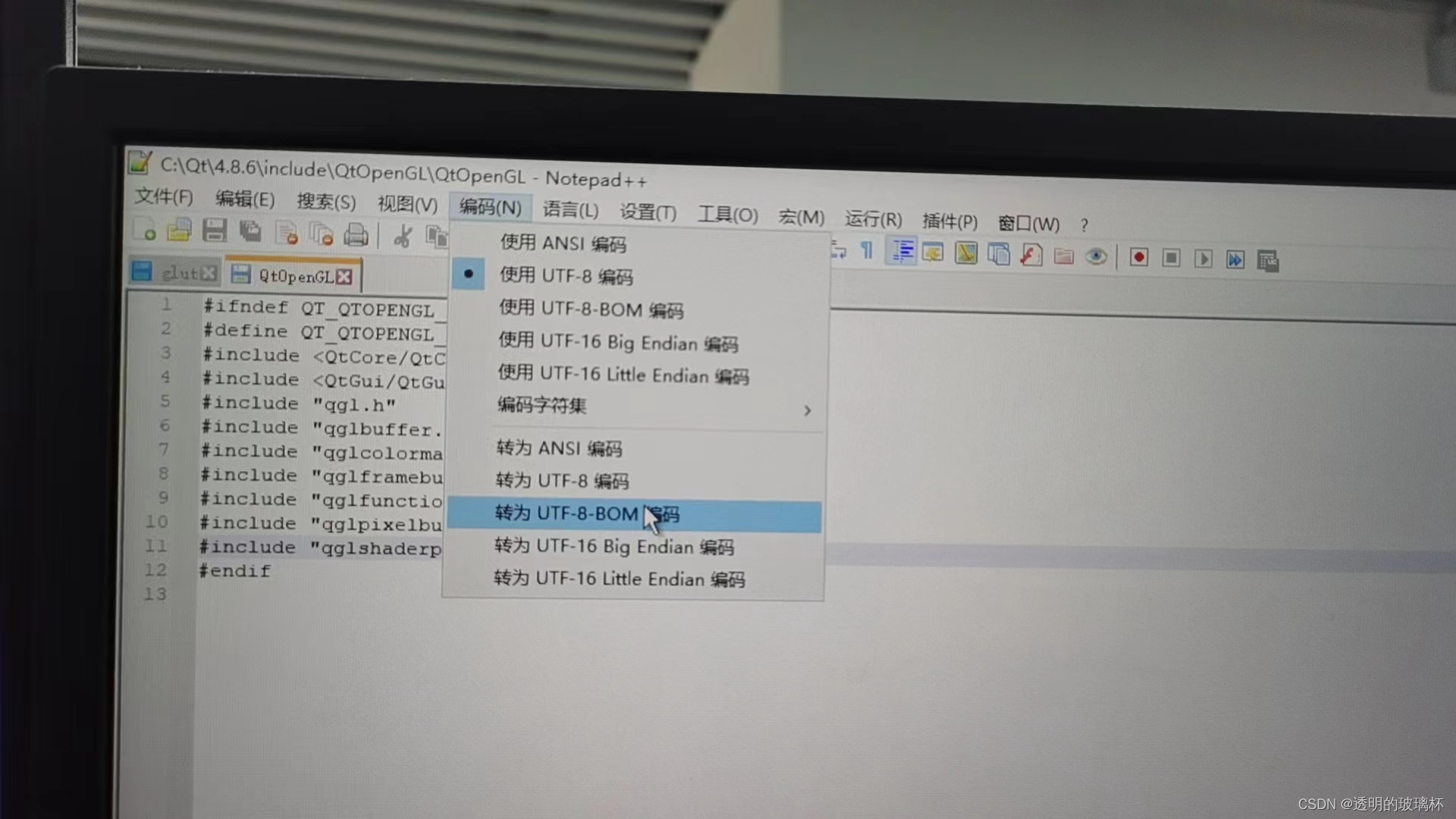
QT+winodow 代码适配调试总结(二)
已经好多年了, linux环境下不同版本的QT程序开发和部署,突然需要适配window环境程序调试,一堆大坑,还真是一个艰巨的任务,可是kpi下的任务计划,开始吧!! 1、首先我们自定义的动态库…...

百家讲坛 | 裴伟伟:企业中安全团队应当如何反馈漏洞
作者简介:裴伟伟,洞源实验室创始人,国家网安基地网络安全行业专家,网安加社区特聘专家,持有CISSP、PMP证书,曾在HITCON、可信云大会、开源产业大会等安全论坛发表演讲。曾任国内某安全实验室负责人、某互金…...

巧用Fiddler中的Comments提升接口测试效率
有没有同学在使用Fiddler时跟我遇到了同样的问题,就是想给某个抓包的请求进行注释!!!但是奇怪的是,根本没有Comments相关信息呀? 设置Comments 设置Comments非常容易,选中一个请求,…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
