ComfyUI流程图、文生图、图生图步骤教学!
前言
leetcode , 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的子数组
[numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
public int minSubArrayLen(int target, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int ans = Integer.MAX_VALUE;int[] sums = new int[n + 1]; //计算前缀和:sums[i] 表示 nums[0]~nums[i-1]的和for (int i = 1; i <= n; i++) {sums[i] = sums[i - 1] + nums[i - 1];}for (int i = 1; i <= n; i++) {int tmp = target + sums[i - 1];// target = sum[b]- sum[a];sum[b] = target + sum[a];int bound = Arrays.binarySearch(sums, tmp);//二分查找if (bound < 0) {bound = -bound - 1;}if (bound <= n) {ans = Math.min(ans, bound - (i - 1));}}return ans == Integer.MAX_VALUE ? 0 : ans;
}
1.jpg
流程图
在熟悉了ComfyUI的各种加载器、采样器、调节器、潜在空间、图像控制等节点后,现在要选用并添加合适的节点构建自己的工作流程图。
ComfyUI还提供了两种方式来加载流程图。
加载json
通过加载他人分享或者自己保存过的json文件(该json保存了流程图所有的节点及其连接信息),如下图所示:

加载原图
通过加载由ComfyUI生成的原图,如下图所示:
资源
对于刚开始不熟悉流程节点和连接信息,可以选择加载别人分享的示例,然后自己进行定制化修改。
在ComfyUI的开源项目中给出了一些在不同场景下的例子,可以参考:

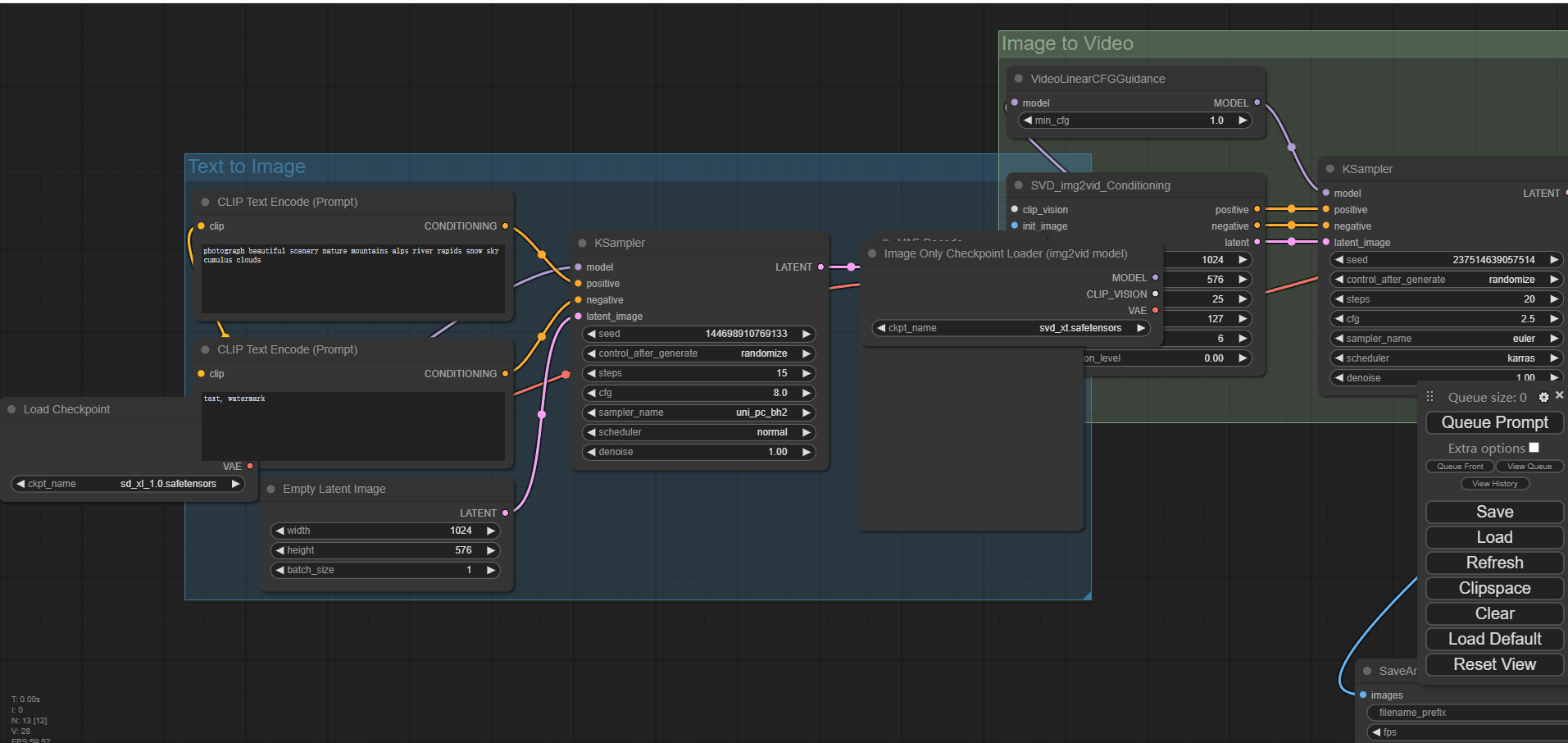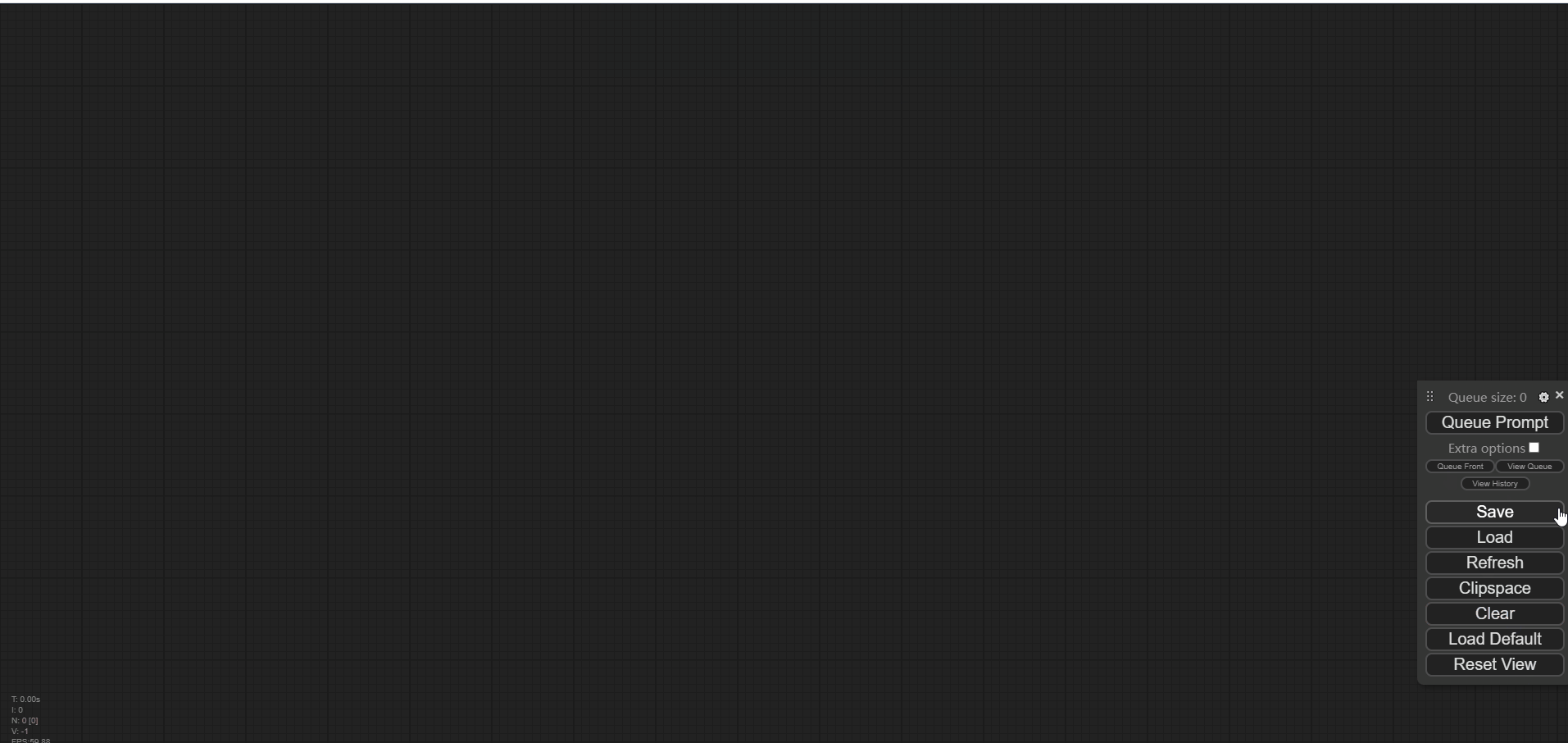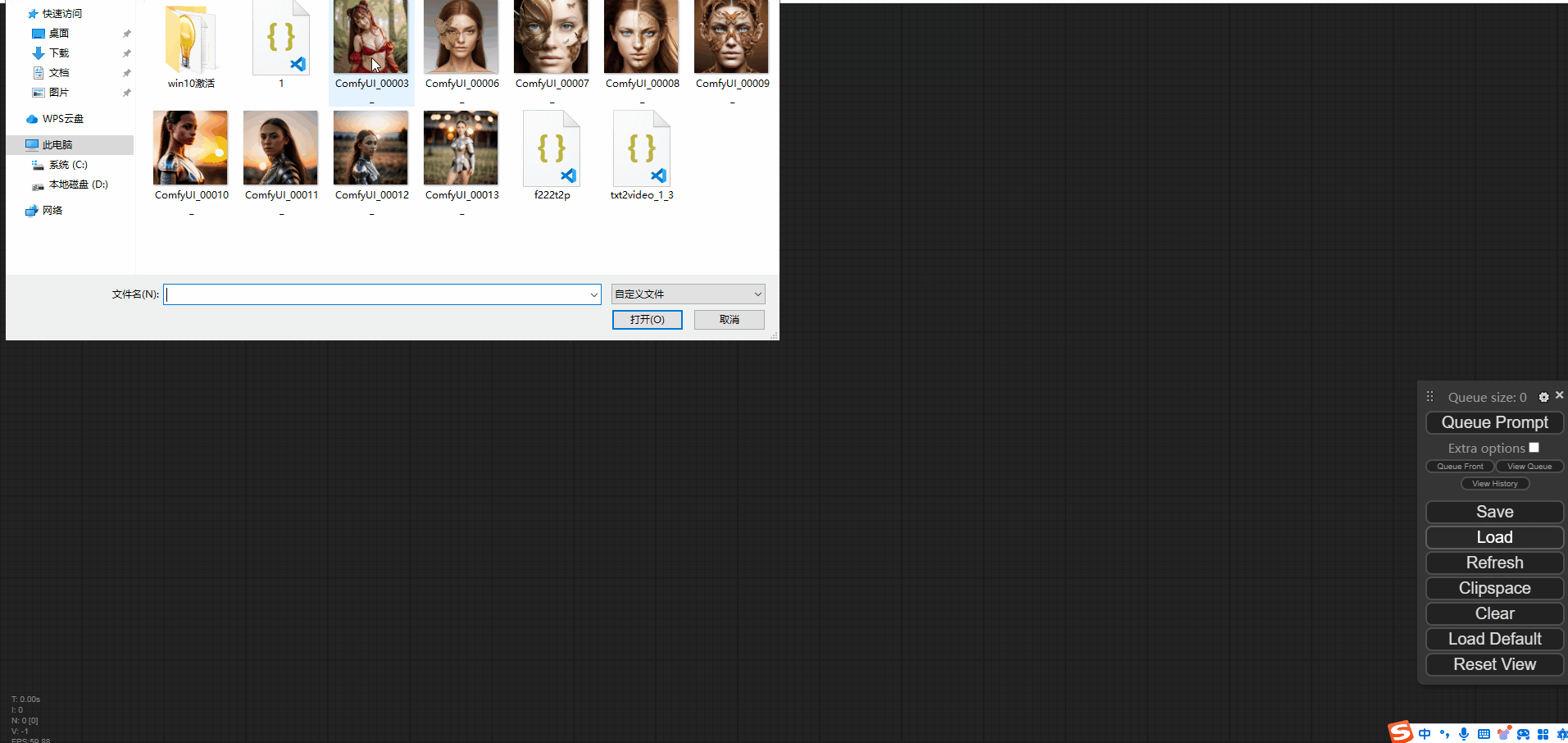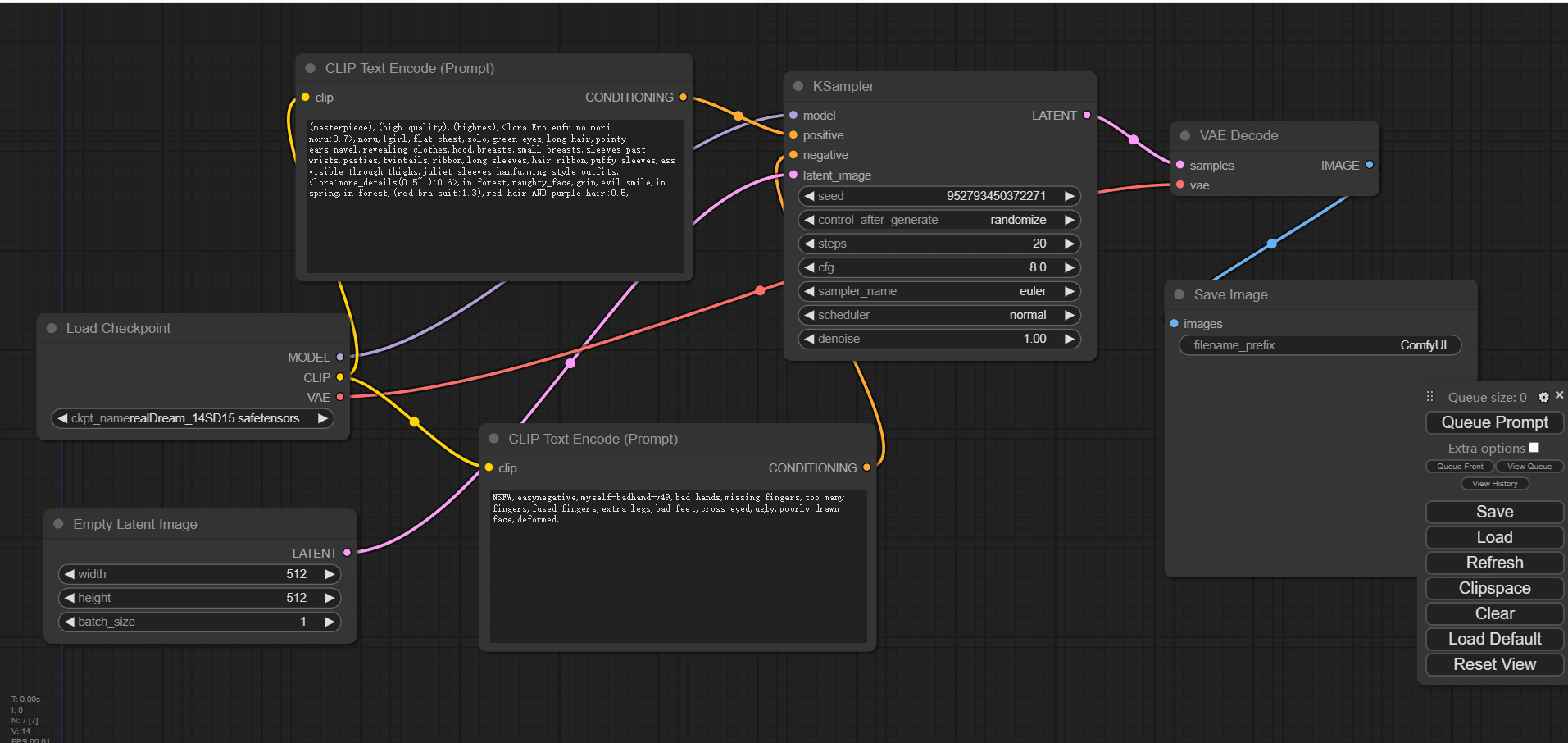
文生图
学习了基础的节点和流程图,利用现有的流程图,在C站上参考了一份提示词:
Prompt:
8k portrait of beautiful cyborg with brown hair, intricate, elegant, highly detailed, majestic, digital photography, art by artgerm and ruan jia and greg rutkowski surreal painting gold butterfly filigree, broken glass, (masterpiece, sidelighting, finely detailed beautiful eyes: 1.2), hdr, (detailed background window to a new dimension, plants and flowers:0.7) lora:more\_details:0.5 infinity, infinite symbol,
Negative prompt:
BadDream, FastNegativeV2
如下图:





生成的结果图,基本符合提示词。可能是没有使用相同模型的原因,与原图有较大的差别,但基本元素都有,原图如下:

图生图
图生图的流程图与上述文生图差不多,只是·将空白图像的输入换成了加载图像·。
选用了ComfyUI的默认图加上述提示词试了一下,效果不太理想,如下图:

·将denoise参数调到0.75·,再试一次,效果有所提升,但还是不符合预期:

这说明在写提示词时,应该也与输入图像有所关联,如图:

可以尝试验证下。
每日一算
leetcode , 238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
为了帮助大家更好地掌握 ComfyUI,我在去年花了几个月的时间,撰写并录制了一套ComfyUI的基础教程,共六篇。这套教程详细介绍了选择ComfyUI的理由、其优缺点、下载安装方法、模型与插件的安装、工作流节点和底层逻辑详解、遮罩修改重绘/Inpenting模块以及SDXL工作流手把手搭建。
由于篇幅原因,本文精选几个章节,详细版点击下方卡片免费领取
一、ComfyUI配置指南
- 报错指南
- 环境配置
- 脚本更新
- 后记
- …
二、ComfyUI基础入门
- 软件安装篇
- 插件安装篇
- …
三、 ComfyUI工作流节点/底层逻辑详解
- ComfyUI 基础概念理解
- Stable diffusion 工作原理
- 工作流底层逻辑
- 必备插件补全
- …
四、ComfyUI节点技巧进阶/多模型串联
- 节点进阶详解
- 提词技巧精通
- 多模型节点串联
- …
五、ComfyUI遮罩修改重绘/Inpenting模块详解
- 图像分辨率
- 姿势
- …

六、ComfyUI超实用SDXL工作流手把手搭建
- Refined模型
- SDXL风格化提示词
- SDXL工作流搭建
- …

由于篇幅原因,本文精选几个章节,详细版点击下方卡片免费领取

相关文章:

ComfyUI流程图、文生图、图生图步骤教学!
前言 leetcode , 209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 …...

CSS基础知识学习指南
CSS基础知识学习指南 1. 介绍 CSS(层叠样式表)是用于描述HTML文档的呈现样式的语言。通过CSS,可以控制网页的布局、颜色、字体等各种样式,使得网页更加美观和用户友好。 2. CSS基础语法 CSS由选择器和声明块组成。选择器用于选…...

力扣hot100 -- 贪心算法
👂 ▶ 逍遥叹 - 胡歌&沈以城【Mashup】 (163.com) 👂 庐州月 - 许嵩 - 单曲 - 网易云音乐 2.7 小时,加上写博客,4 道题,😂 -- 希望二刷时,可以 3 小时,8 道题.... 目录 &…...

P2P文件传输协议介绍
P2P文件传输协议是一种基于对等网络(Peer-to-Peer,简称P2P)的文件共享和传输技术。以下是关于P2P文件传输协议的详细介绍: 一、定义与原理 P2P文件传输协议允许网络中的各个节点(即计算机或其他设备)之间…...

Spring Boot集成Spring Mobile快速入门Demo
1.什么是Spring Mobile? Spring Mobile是一个基于Spring Web MVC框架扩展的一个针对不同移动终端的应用开发框架。通过它我们在适配不同终端方面,就不用费劲心思了。 Spring Mobile的主要功能 自动设备检测: Spring Mobile在 server端内置了一个设备解…...

走进开源企业 | 湖南大学OpenHarmony技术实训活动在开鸿智谷顺利举办!
6月24日-6月26日,2024开放原子校源行之湖南大学信息科学与工程学院师生走进开源企业实训交流活动顺利落下帷幕。湖南大学信息科学与工程学院的师生代表团一行90人参与了湖南开鸿智谷数字产业有限公司(以下简称“开鸿智谷”)与母公司拓维信息系…...
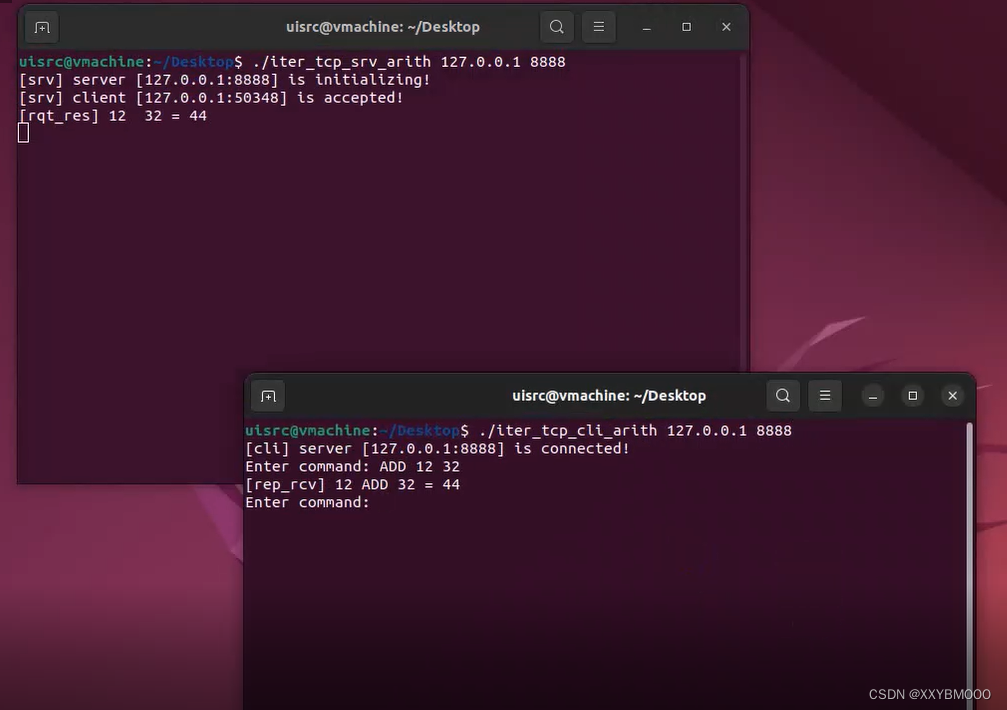
TCP单进程循环服务器程序与单进程客户端程序
实验目的 理解并掌握以下内容: 网络进程标识(即套接字地址)在Linux中的数据结构与地址转换函数。网络字节序与主机字节序的定义、转换以及相关函数在网络编程中的应用。数据结构内存对齐的基本规则,以及基于数据结构构建PDU的基本方法。TCP单进程循环服务器与单进程客户端的…...
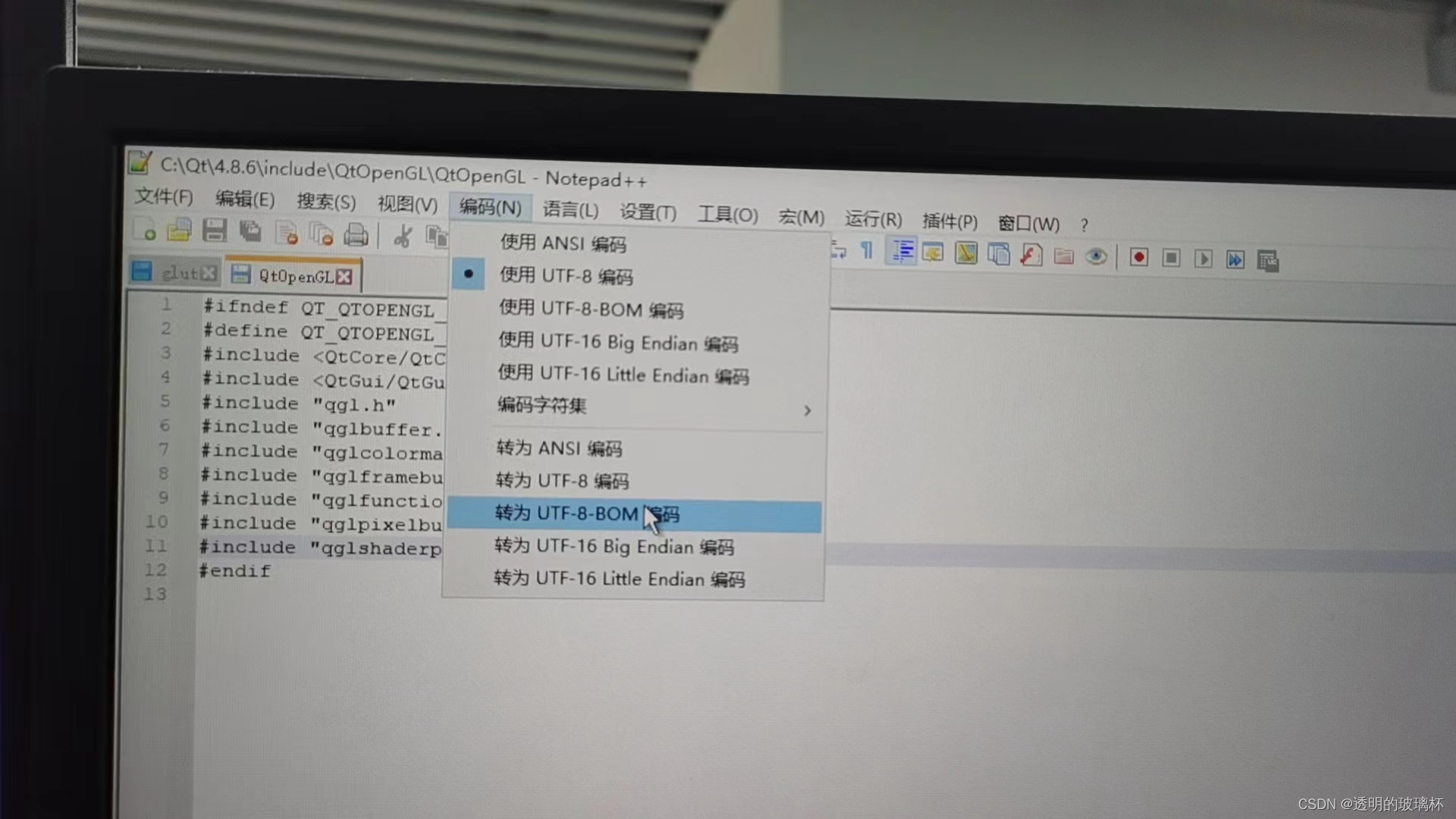
QT+winodow 代码适配调试总结(二)
已经好多年了, linux环境下不同版本的QT程序开发和部署,突然需要适配window环境程序调试,一堆大坑,还真是一个艰巨的任务,可是kpi下的任务计划,开始吧!! 1、首先我们自定义的动态库…...

百家讲坛 | 裴伟伟:企业中安全团队应当如何反馈漏洞
作者简介:裴伟伟,洞源实验室创始人,国家网安基地网络安全行业专家,网安加社区特聘专家,持有CISSP、PMP证书,曾在HITCON、可信云大会、开源产业大会等安全论坛发表演讲。曾任国内某安全实验室负责人、某互金…...

巧用Fiddler中的Comments提升接口测试效率
有没有同学在使用Fiddler时跟我遇到了同样的问题,就是想给某个抓包的请求进行注释!!!但是奇怪的是,根本没有Comments相关信息呀? 设置Comments 设置Comments非常容易,选中一个请求,…...

停车场车牌识别计费系统,用Python如何实现?
关注星标,每天学习Python新技能 前段时间练习过的一个小项目,今天再看看,记录一下~ 项目结构 说明: datefile文件夹:保存车辆信息表的xlsx文件 file文件夹:保存图片文件夹。ic_launcher.jpg是窗体的右上角…...

Linux内核——Linux内核体系模式(二)
1 Linux系统的中断机制 Linux内核将中断分为两类:硬件中断和软件中断(异常)。每个中断是由0-255之间的一个数字进行标识。 中断int0-int31(0x00-0x1f)作为异常int32-int255由用户自己设定 int32-int47对应与8259A中断…...
简单异常处理器)
Spring MVC的高级功能——异常处理(一)简单异常处理器
一、HandlerExceptionResolver接口 如果希望对Spring MVC中所有异常进行统一处理,可以使用Spring MVC提供的异常处理器HandlerExceptionResolver接口。Spring MVC内部提供了HandlerExceptionResolver的实现类SimpleMappingExceptionResolver。它实现了简单的异常处理…...

【面试干货】Static关键字的用法详解
【面试干货】Static关键字的用法详解 1、Static修饰内部类2、Static修饰方法3、Static修饰变量4、Static修饰代码块5、总结 💖The Begin💖点点关注,收藏不迷路💖 在Java编程语言中,static是一个关键字,它可…...
软件工程实验
实验环境和需求 用户可以对相片进行按类别管理,用户可以设定不同的类别,然后上传照片到相应的类别中,并能进行照片的删除,注释 运行 运行并访问 localhost 8090,图片在数据库中的信息是D:/upgrade 后面的内容 se…...

对于复杂的网页布局,如多列布局和网格布局,CSS 有哪些最佳实践和技巧?
对于复杂的网页布局,如多列布局和网格布局,以下是一些CSS的最佳实践和技巧: 使用Flexbox或CSS Grid布局:Flexbox和CSS Grid是两个强大的CSS布局模型,可用于实现复杂的网页布局。Flexbox适用于单行或单列布局࿰…...

Spring Boot中集成Redis实现缓存功能
Spring Boot中集成Redis实现缓存功能 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨如何在Spring Boot应用程序中集成Redis,实现…...
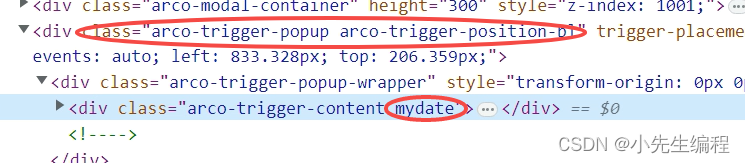
arco disign vue 日期组件的样式穿透
问题描述: 对日期组件进行样式穿透. 原因分析: 如图,日期组件被展开时它默认将dom元素挂载到body下, 我们的页面在idroot的div 里层, 里层想要穿透外层是万万行不通的. 解决问题: 其实官网提供了参数,但是并没有提供例子, 只能自己摸索着过河. 对于日期组件穿透样式,我们能…...
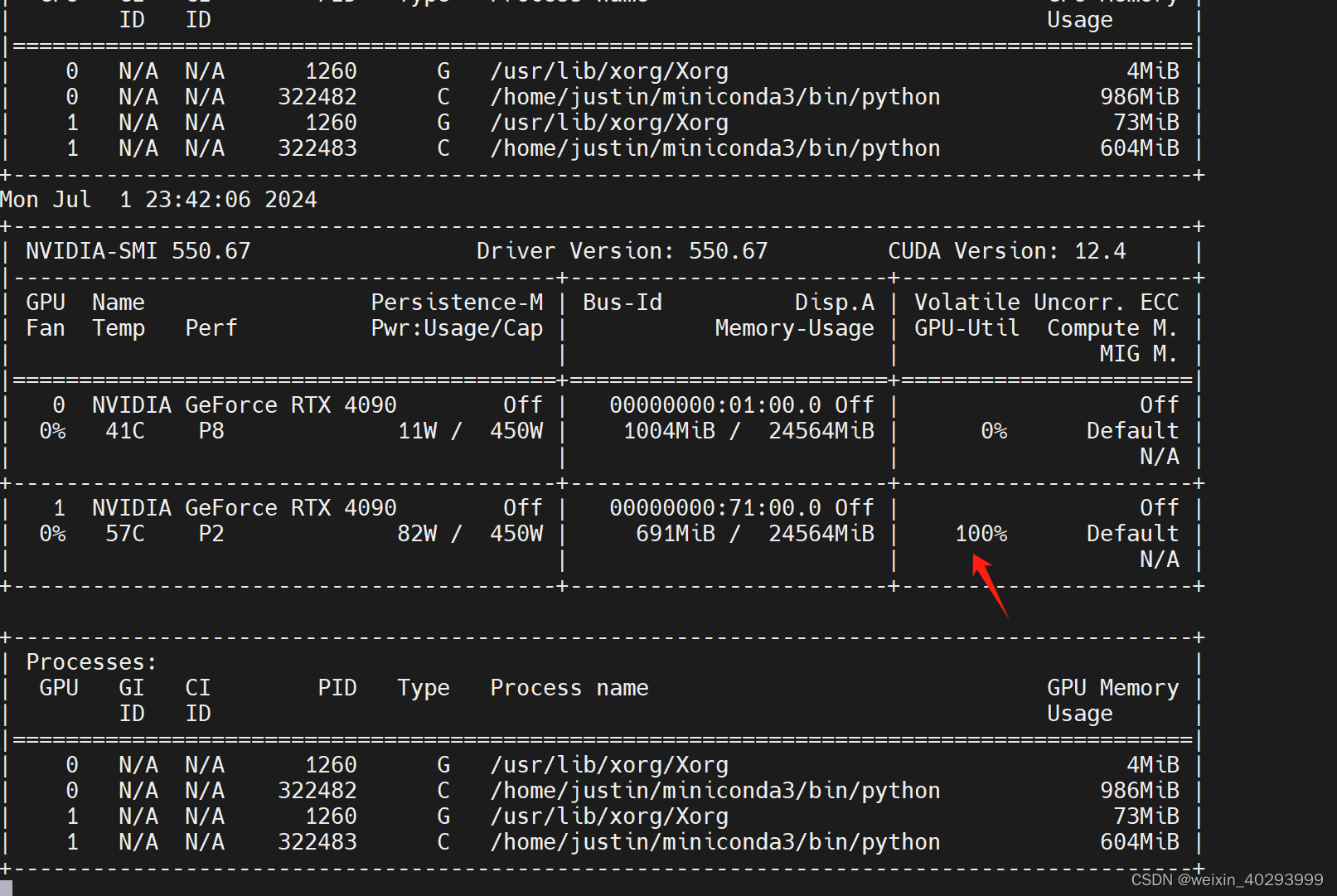
【深度学习】pytorch训练中的一个大坑
使用的命令:iostat -x 5 可以看到 ssd的利用率已经满了。 之前在的数据集放在了 hdd上,训练结果特别慢。 所以我把它移动到了ssd上,然后训练参数用的 resume, 但是!!!!它把历史记住…...
)
python全局解释器锁(GIL)
文章目录 1.cpu工作方式2.python全局解释器锁与多线程3.其他语言的多线程4.如何解决假的多线程 1.cpu工作方式 先来先服务(First Come, First Served,FCFS): 最简单的调度算法,按照作业或进程到达的顺序依次执行。没有…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

