每周算法：有向图强连通分量

题目链接

受欢迎的牛

题目描述

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 $A$ 喜欢 $B$，$B$ 喜欢 $C$，那么 $A$ 也喜欢 $C$。牛栏里共有 $N$ 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入格式

第一行：两个用空格分开的整数：$N$ 和 $M$。

接下来 $M$ 行：每行两个用空格分开的整数：$A$ 和 $B$，表示 $A$ 喜欢 $B$。

输出格式

一行单独一个整数，表示明星奶牛的数量。

样例 #1

样例输入 #1

4 4
1 2
2 3
3 4
4 2

样例输出 #1

3

样例输入 #2

6 6
1 2
2 3
3 4
4 2
4 5
4 6

样例输出 #2

0

提示

【数据范围】

对于 $10\%$ 的数据，$N\le 20$，$M\le 50$。

对于 $30\%$ 的数据，$N\le 10^3$，$M\le 2\times 10^4$。

对于 $70\%$ 的数据，$N\le 5\times 10^3$，$M\le 5\times 10^4$。

对于 $100\%$ 的数据，$1\le N\le 10^4$，$1\le M\le 5\times 10^4$。

算法思想

根据题目描述，牛栏里共有 $N$ 头奶牛，给定一些奶牛之间的爱慕关系，这些爱慕关系是可以传递的。被所有奶牛喜欢的奶牛就是一头明星奶牛，求多少头奶牛可以当明星。

从测试样例#1分析，如下图所示，顶点$2,3,4$构成了有向图的一个强连通分量，在强连通分量中任意两点之间都是可达的。由于顶点$1$能够到达这个强连通分量，因此顶点$2,3,4$都可以当明星。

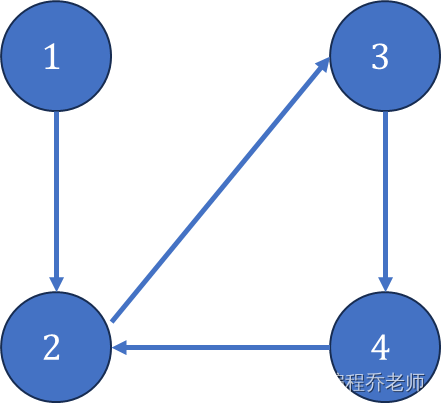
强连通分量

在有向图$G$中，如果两个顶点$u,v$间存在一条$u$到$v$的路径，也存在一条$v$到$u$的路径，则称这两个顶点式强连通的（strongly connected）。

如果有向图$G$的任意两个顶点都强连通，则称$G$是一个强连通图。有向非强连通图的极大强连通子图，称为强连通分量（strongly connected component）。

$G$是一个极大强连通子图，当且仅当$G$是一个强连通子图且不存在另一个强连通子图$G^{\prime }$，使得$G$是$G^{\prime }$的真子集。

下图中，子图 { 1 , 2 , 3 , 4 } \{1,2,3,4\} {1,2,3,4}为一个强连通分量，因为顶点$1,2,3,4$两两可达， { 5 } \{5\} {5}， { 6 } \{6\} {6}也分别是两个强连通分量。

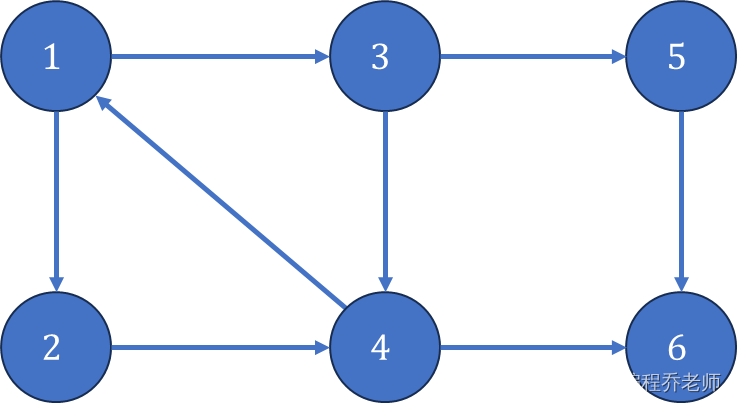
应用

若将有向图中的强连通分量都缩为一个点，则原图会形成一个DAG（有向无环图），如下图所示

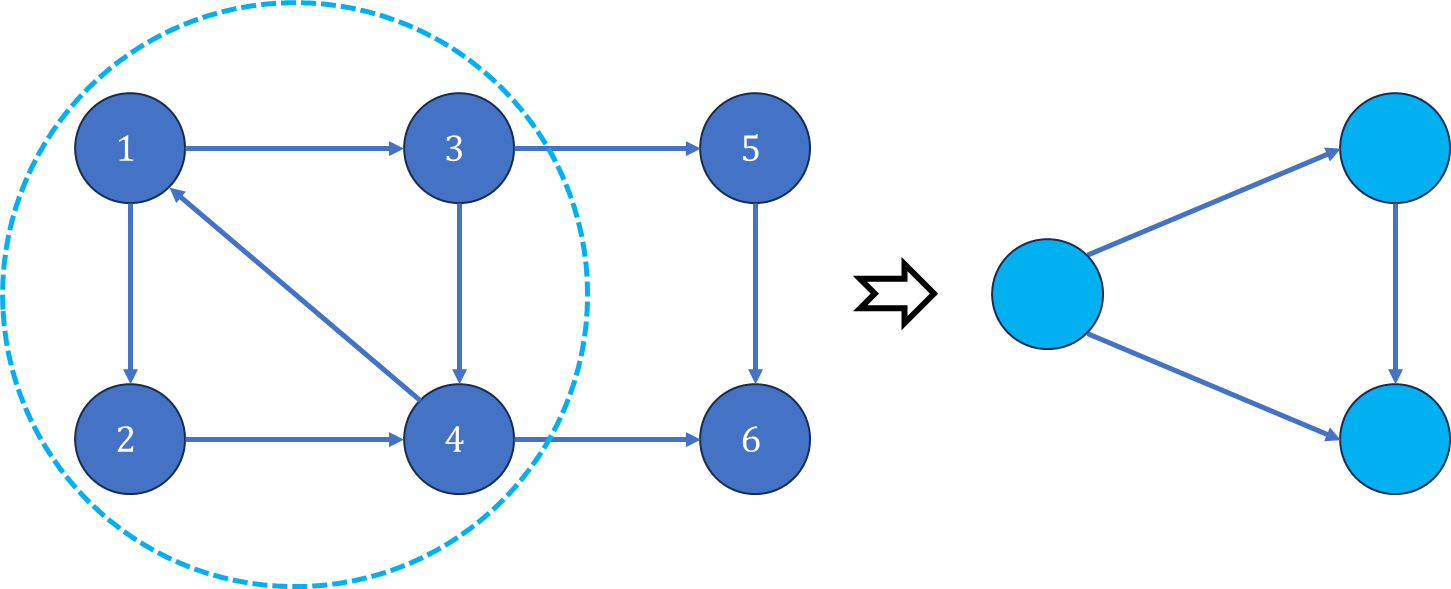
根据上述分析，可以将有向图中的强连通分量都缩为一个点，形成一个DAG，找到出度为$0$点，求出其中点的个数就是答案。

注意，如果出度为$0$的点的个数不惟一，至少存在另外一个终点无法相互到达它，则说明不存在奶牛可以当明星。如测试样例#2所示：

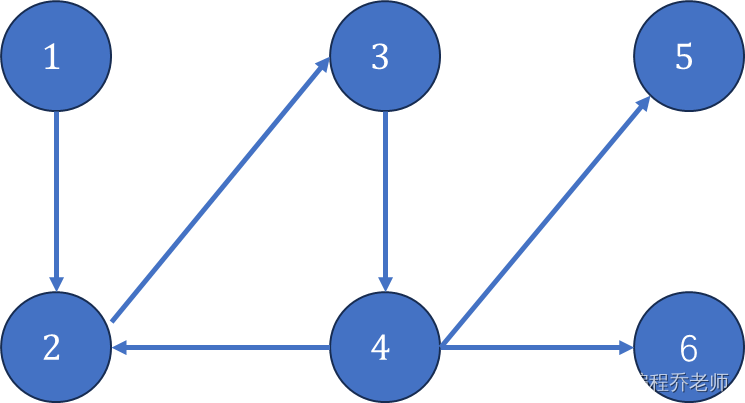
Tarjan算法

Robert Tarjan提出的了求解有向图强连通分量的线性时间的算法，即Tarjan算法。

算法原理

对每个点定义两个时间戳$timestamp$：

1. dfn[u]表示遍历到$u$的时间戳
2. low[u]表示从点$u$开始走，所能遍历的最小的时间戳

如果$u$是其所在的连通分量的最高点（时间戳最小），那么dfn[u] == low[u]。

算法实现

对有向图$G$的每个顶点$u$进行深度优先遍历：

1. dfn[u] = low[u] = 1
2. 将$u$点压入栈
3. 遍历$u$所有邻接点
4. 如果当前点$v$没有被遍历过，深度优先遍历$v$，求出low[v]，使用low[v]更新low[u]
5. 如果当前点$v$被遍历过但是还在栈中（即还没有遍历完$v$所在的强联通分量），使用dfn[v]更新low[u]
6. 遍历完$u$的所有连接点后，如果发现dfn[u] == low[u]，说明$u$是其所在的连通分量的最高点
7. 将栈顶所有与$u$连通的点弹出，就是$u$所在强连通分量的点。

缩点

缩点是将每个强连通分量看作一个点，通过有向边将他们连接起来，得到一个有向无环图（DAG），也就是拓扑图。

实现步骤

1. 遍历每个顶点$u$
2. 遍历$u$的每个邻点$v$
3. 如果$u$和$v$不在同一个强连通分量中，添加一条从id[u]到id[v]的有向边，id[u]表示$u$所在的强连通分量的编号。

拓扑序

做完Tarjan算法后，进行缩点之后的强连通分量已经按照其编号递减的顺序完成拓扑序。

因为深度优先搜索把一个强连通分量中所有点找出之后，会给它们设置同一个编号。并且当前编号的强连通分量不会有其它还未搜索到的后继强连通分量，也就是说它的后继都已经处理完成。因为在Tarjan算法中，后继结点后入栈，所以会先被弹出栈进行处理。

既然强连通分量已完成拓扑排序，那么：

1. 如果在这个拓扑图中至少存在两个点的出度为0（终点无后继），那么就不存在被除自己之外的所有牛认为是受欢迎的牛，至少有另外一个终点没有认为它受欢迎。
2. 如果只存在一个点其出度为0，那么这个点所代表的强联通分量中的所有牛都是被除自己之外的所有牛认为是受欢迎的牛。因为在该强连通分量内部，所有点都是连通的；在该强连通分量外部，这种关系是具有传递性，最终会沿着拓扑序走到该强连通分量。

时间复杂度

Tarjan算法的时间复杂度为$O(n+m)$，其中$n$为顶点数，$m$为边数。

代码实现

#include <bits/stdc++.h>
using namespace std;const int N = 10010, M = 50010;int n, m;
int h[N], e[M], ne[M], idx;
//dfn[i]表示结点i的时间戳
//lowe[i]表示结点i能回溯到的最早时间戳
int dfn[N], low[N], timestamp; //时间戳
//栈中当前还没有搜索完的强连通分量的所有点
int stk[N], top;
//in_stk[i]表示结点i是否在栈中
int in_stk[N];
//scc_cnt表示强连通分量的数量
int scc_cnt;
//id[i]表示结点i所在的强连通分量编号
int id[N];
//si[i]表示编号为i的强联通分量中点的数量
int si[N];
//dout[i]表示编号为i的强连通分量的出度
int dout[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void tarjan(int u)
{dfn[u] = low[u] = ++timestamp;stk[++ top] = u, in_stk[u] = 1; //将u入栈//遍历i的所有邻边for(int i = h[u]; ~i; i = ne[i]){int v = e[i];//如果v点还没有遍历过if(!dfn[v]){tarjan(v); //深度优先搜索v//如果low[v]更小，则使用low[v]更新low[u]//因为u可以到达v，所以v能回溯到时间戳，u也必然能到low[u] = min(low[u], low[v]);}else //v点已经遍历过了{//如果v已经搜索过但还在栈中，说明v是u的后向边或者横叉边连接的点//那么v点的时间戳一定小于u点的时间戳。if(in_stk[v]) low[u] = min(low[u], dfn[v]);}}//如果u能回溯到的最早时间戳就是自己，//那么u必然是其所在强连通分量最早被访问的点if(dfn[u] == low[u]){scc_cnt ++;int v; // 栈中该强连通分量中的点do{v = stk[top --];in_stk[v] = 0;id[v] = scc_cnt;si[scc_cnt]++; //统计该强连通分量中点的数量}while(u != v);}
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);while(m --){int a, b;cin >> a >> b;add(a, b);}//处理强连通分量for(int i = 1; i <= n; i++){if(!dfn[i]) tarjan(i);}//遍历所有点，计算强连通分量的出度for(int u = 1; u <= n; u++)for(int i = h[u]; ~i; i = ne[i]){int v = e[i];//u和v不属于同一个强连通分量if(id[u] != id[v]) dout[id[u]]++;}//处理所有出度为0的强连通分量，累加所有出度为0的强连通分量中的点的数量。int sum = 0, zeros = 0;for(int i = 1; i <= scc_cnt; i ++)if(dout[i] == 0){zeros++;sum += si[i];if(zeros > 1){sum = 0;break;}}cout << sum << endl;return 0;
}