DP:子序列问题
文章目录
- 什么是子序列
- 子序列的特点
- 举例说明
- 常见问题
- 关于子序列问题的几个例题
- 1.最长递增子序列
- 2.摆动序列
- 3.最长递增子序列的个数
- 4.最长数对链
- 5.最长定差子序列
- 总结

什么是子序列
在计算机科学和数学中,子序列(Subsequence)是指从一个序列中删除一些元素(可以是零个或多个),但不改变其余元素相对顺序后形成的新序列。
子序列的特点
元素的相对顺序保持不变。
可以删除零个或多个元素。
一个序列的子序列可以为空序列,即不包含任何元素。
举例说明
设有序列 S = [A, B, C, D, E],则其子序列可以有:
删除零个元素:[A, B, C, D, E](即自身)
删除一个元素:[A, B, C, D]、[A, B, C, E]、[A, B, D, E]、[A, C, D, E]、[B, C, D, E]
删除两个元素:[A, B, C]、[A, B, D]、[A, B, E]、[A, C, D]、[A, C, E]、[A, D, E]、[B, C, D]、[B, C, E]、[B, D, E]、[C, D, E]
删除三个元素:[A, B]、[A, C]、[A, D]、[A, E]、[B, C]、[B, D]、[B, E]、[C, D]、[C, E]、[D, E]
删除四个元素:[A]、[B]、[C]、[D]、[E]
删除所有元素:[](空序列)
常见问题
子序列问题在算法设计和编程竞赛中非常常见。以下是几种经典问题:
最长公共子序列(LCS):给定两个序列,找出它们的最长公共子序列。动态规划是解决这个问题的常用方法。
最长递增子序列(LIS):给定一个序列,找出其中最长的递增子序列。可以使用动态规划或贪心算法结合二分查找解决。
子序列和问题:给定一个序列,找出所有和为特定值的子序列。可以使用回溯法或动态规划解决。
根据我上面的介绍,可以总结,大多数子序列问题其实都可以用DP的算法来解决。
关于子序列问题的几个例题
1.最长递增子序列
题目链接
题目:
样例 输出和输入:
首先根据上述子序列的描述,这道题就很容易理解了,就是 让我们求给定数组的最长的递增子序列。
算法原理:
状态表示:dp[i]表示以i位置为结尾的所有子序列中最长的那个子序列的长度。
状态转移方程:

首先我们要求状态转移方程就要看i位置的状态,我们要确定i位置的状态,是不是应该将0到i-1位置遍历一遍,然后将当中的最长子序列求出来然后再加上当前位置的长度1就可以了,这是当子序列长度大于1的时候,还有一种情况是长度等于1的时候,长度等于1的时候,可以默认看做一个子序列,所以dp[i]就等于1,当长度大于1的时候,这种情况,我们先用一个变量j将0到i-1位置的最长子序列遍历出来,然后再+1,所以状态转移方程:dp[i] = max(dp[j]+1,dp[i])。
初始化:因为单独一个元素就可以看做一个递增的子序列,所以DP表中的值可以全部初始化为1.
代码展示:
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i-1;j >= 0;j--){if (nums[j] < nums[i]){dp[i] = max(dp[j]+1,dp[i]);}dpmax=max(dp[i],dpmax);}}return dpmax;}
};
运行结果:
2.摆动序列
题目链接
题目:
样例 输出和输入:
这道题让我们求摆动序列的最长的子序列的长度,首先我们要搞清楚,什么是摆动序列:
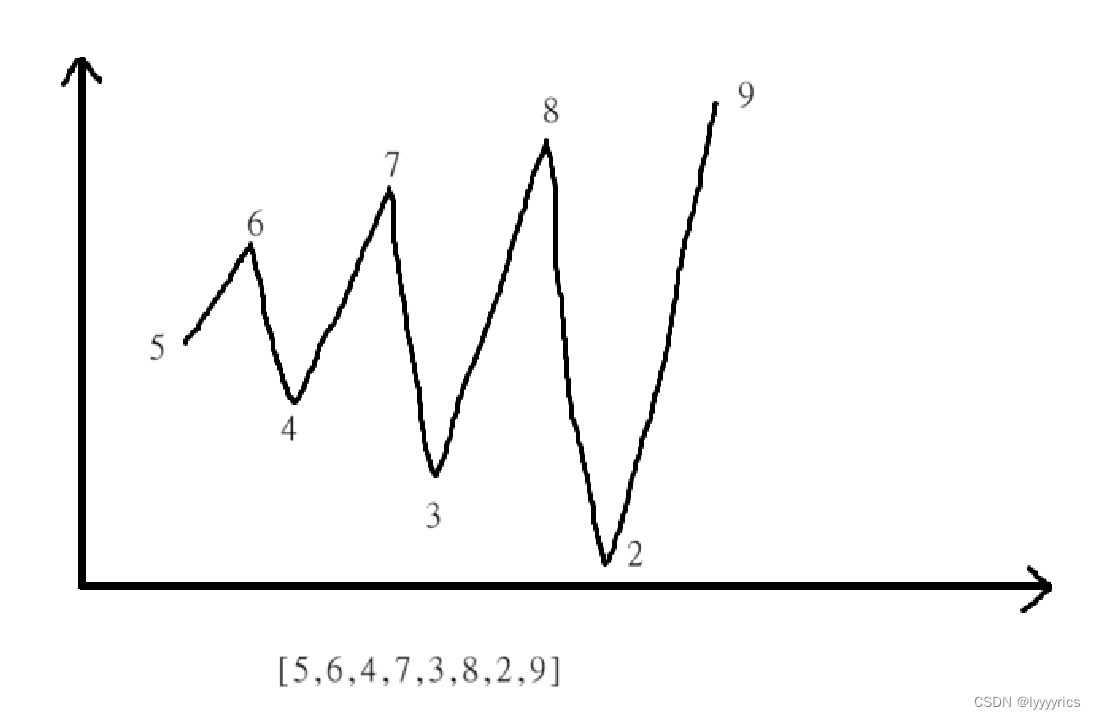
上面就是一个摆动序列。
算法原理:
这道题首先要求摆动序列,我们上个专题已经做过类似的题了,就像湍流数组一样,这道题很显然,我们需要两个状态,一个状态是向下的状态,一个状态是向上的状态,这里定义f[i]是向上的状态,g[i]是向下的状态。
状态表示:f[i]是以i位置为结尾的子序列中长度最长且最后一个状态是向上的最长子序列的长度,g[i]表示以i位置为结尾最后的子序列中最后一个状态向下的最长子序列的长度。
状态转移方程:首先对f[i]分析:
所以这里f[i]的状态转移方程:f[i] = max(g[j] + 1, f[i]),同理也可以求出g[i]的状态转移方程:g[i] = max(f[j] + 1, g[i])
代码展示:
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n,1), g(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (nums[j] > nums[i]){g[i] = max(f[j] + 1, g[i]);}else if (nums[j] < nums[i]){f[i] = max(g[j] + 1, f[i]);}dpmax = max(max(dpmax, f[i]), g[i]);}}return dpmax;}
};
运行结果:
3.最长递增子序列的个数
题目链接
题目:
样例 输出和输入:
这道题相对于第一道题换了一个问法。这道题是求最长子序列的个数
算法原理:
状态表示:首先我们先定义一个状态,看这个状态能推下去吗,dp[i]表示以i位置为结尾的所有子序列中,最长子序列的个数。
状态转移方程:首先这里就出问题了 ,这里我们根本不知道最长的子序列是什么,因为根本没有记录的,所以这里根本就推不出来,所以还得加一个len[i],len[i]表示以i位置为结尾的所有子序列中最长子序列的长度,将dp[i]改为count[i],count[i]表示以i位置为结尾的所有子序列中最长的子序列的个数。接下来来推状态转移方程,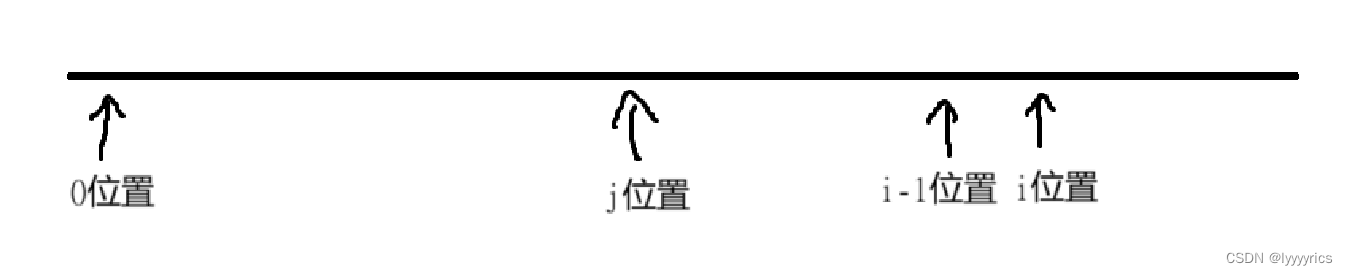
有三种情况,当我们遍历的len[j]+1==len[i],意思就是0到i-1位置的子序列中加上当前的长度和之前的最长的子序列是相同的,这里我们应该把以j位置为结尾的最长子序列的个数全部加到count[i]]中。这里画图表示
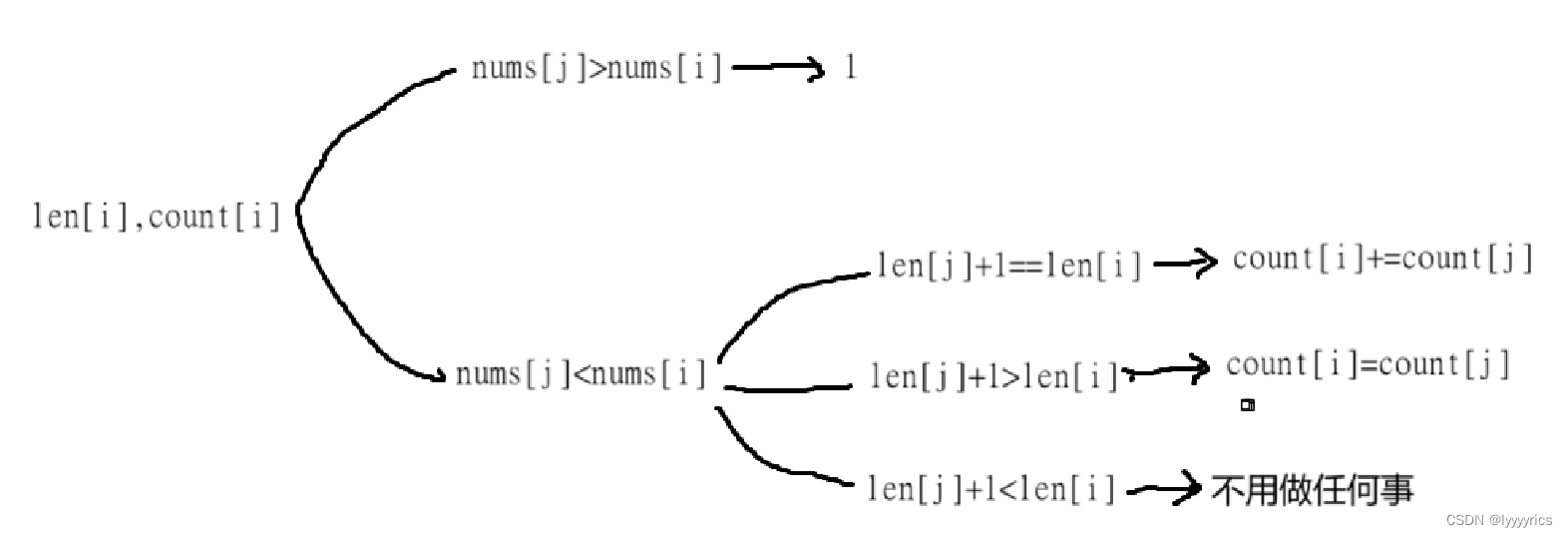
根据这些情况可以将表填完,但是,我们还需要 一个retlen和一个retcount更新每次的最长子序列的长度和最长子序列的个数。
这里也分为三种情况,和上面的情况相同,只需要每次遍历完一个位置,更新结果即可。
代码展示:
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n,1), count(n,1);//统计每次的每次的最终结果int retlen = 1, retcount = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){//当出现递增的时候if (nums[j] < nums[i]){//判断如果加上递增的那一个和当前最长的长度还是一样的则需要更新countif (len[j] + 1 == len[i])count[i] += count[j];//如果加上当前的一个元素比比之前的最长的子序列要长,则重新规划长度else if (len[j] + 1 > len[i])count[i] = count[j],len[i] = len[j];}}//统计每次的结果,如果len和结果的len相同,则直接用count累加if (retlen == len[i])retcount += count[i];//如果len比结果的len要大,则直接重置结果len和结果的countelse if (retlen < len[i])retcount = count[i], retlen = len[i];}return retcount;}
};
运行结果:
4.最长数对链
题目链接
题目:
样例 输出和输入:
这道题其实和求最长子序列的长度是相同的题,但是换了一个形式而已,根据题目条件我们可以得知什么是数对链:
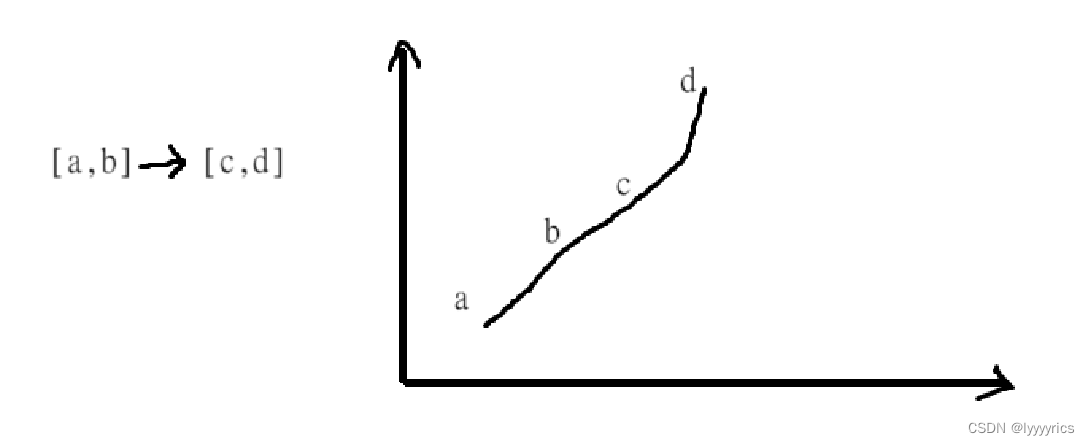
数对连就要满足上述条件
算法原理:
预处理:首先我们得将数组排序,排序的规则,只需要比较每个数对的第一个元素的大小即可,因为每个数对都是单增的,如果我们排序之后保证了a>c,那么d>c是绝对大于前一个数对的,所以这里只需要根据前一个数排序即可。
状态表示:这里dp[i]表示以i位置为结尾的所有数对链中最长的那个数对链的长度。
状态转移方程:分两种情况:
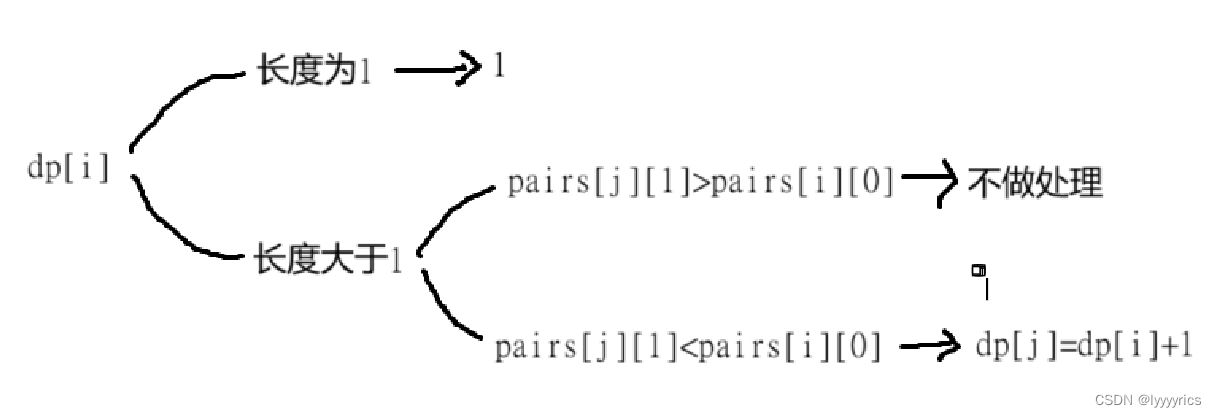
代码展示:
class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (pairs[j][1] < pairs[i][0]){dp[i] = max(dp[j] + 1, dp[i]);}ret = max(dp[i], ret);}}return ret;}
};
运行结果:
5.最长定差子序列
题目链接
题目:
样例 输出和输入:
这道题给定一个difference,让我们求出数组中的差为difference的最长的子序列的长度
算法原理:
状态表示:dp[i]表示以i位置为结尾的所有子序列中的最长的等差子序列,且差值是difference。
状态转移方程:首先我们可以分析一下,我们可以选择从0位置开始遍历寻找和i位置之差是difference的数,这里的dp表其实我们可以借助hash表来充当,因为每次我们都得去前面找和i位置差值是difference的数,所以这里hash表既可以充当dp表,也可以将前一个位置和当前位置的差值是difference的数存起来。
这里的状态转移方程:hash[arr[i]] = hash[arr[i] - difference] + 1这里如果没有在hash表中找到前一个位置差值是difference值的数,则hash[arr[i] - difference]就是0,所以也免去了这种情况,由于我们找的是离i位置最近的前一个位置,这里也可以用hash表解决,因为,我们是从左到右遍历的,这就使得后一个位置每次都是覆盖了前一个位置的值,每次都是最新的状态值。
代码展示:
class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;//arr[i]----dp[i]hash[arr[0]] = 1;int ret = 1;for (int i = 1;i < arr.size();i++){//需要的最后一个b的值,这个hash能保证,因为从左到右遍历,前面的值已经被覆盖了hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};
运行结果:
总结
通过本文对子序列问题的探讨,我们深入理解了动态规划在解决此类问题中的重要性。无论是经典的最长公共子序列(LCS)问题,还是最长递增子序列(LIS)问题,动态规划都展示了其强大的解题能力。通过将问题分解为更小的子问题,并记录这些子问题的解,我们能够高效地找到最优解,避免重复计算。
此外,我们还见识了动态规划解决子序列问题的多种变体及其实际应用。这不仅拓宽了我们对算法设计的视野,也提升了我们在面对复杂问题时的解决能力。子序列问题不仅在理论上具有重要意义,也在现实世界中的许多领域,如生物信息学、文本处理和数据分析中有着广泛的应用。
希望通过本文的讲解,读者能对动态规划在子序列问题中的应用有更深的理解,并能将这些技术应用于实际编程中,解决更多实际问题。动态规划的学习不仅仅局限于特定问题,更是培养一种思维方式,一种解决复杂问题的系统方法。愿大家在未来的算法学习和应用中继续精进,取得更大的进步。
相关文章:

DP:子序列问题
文章目录 什么是子序列子序列的特点举例说明常见问题 关于子序列问题的几个例题1.最长递增子序列2.摆动序列3.最长递增子序列的个数4.最长数对链5.最长定差子序列 总结 什么是子序列 在计算机科学和数学中,子序列(Subsequence)是指从一个序列…...

Spring Data与多数据源配置
Spring Data与多数据源配置 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨如何在Spring Data中配置和使用多个数据源。 在现代应用程序中&…...
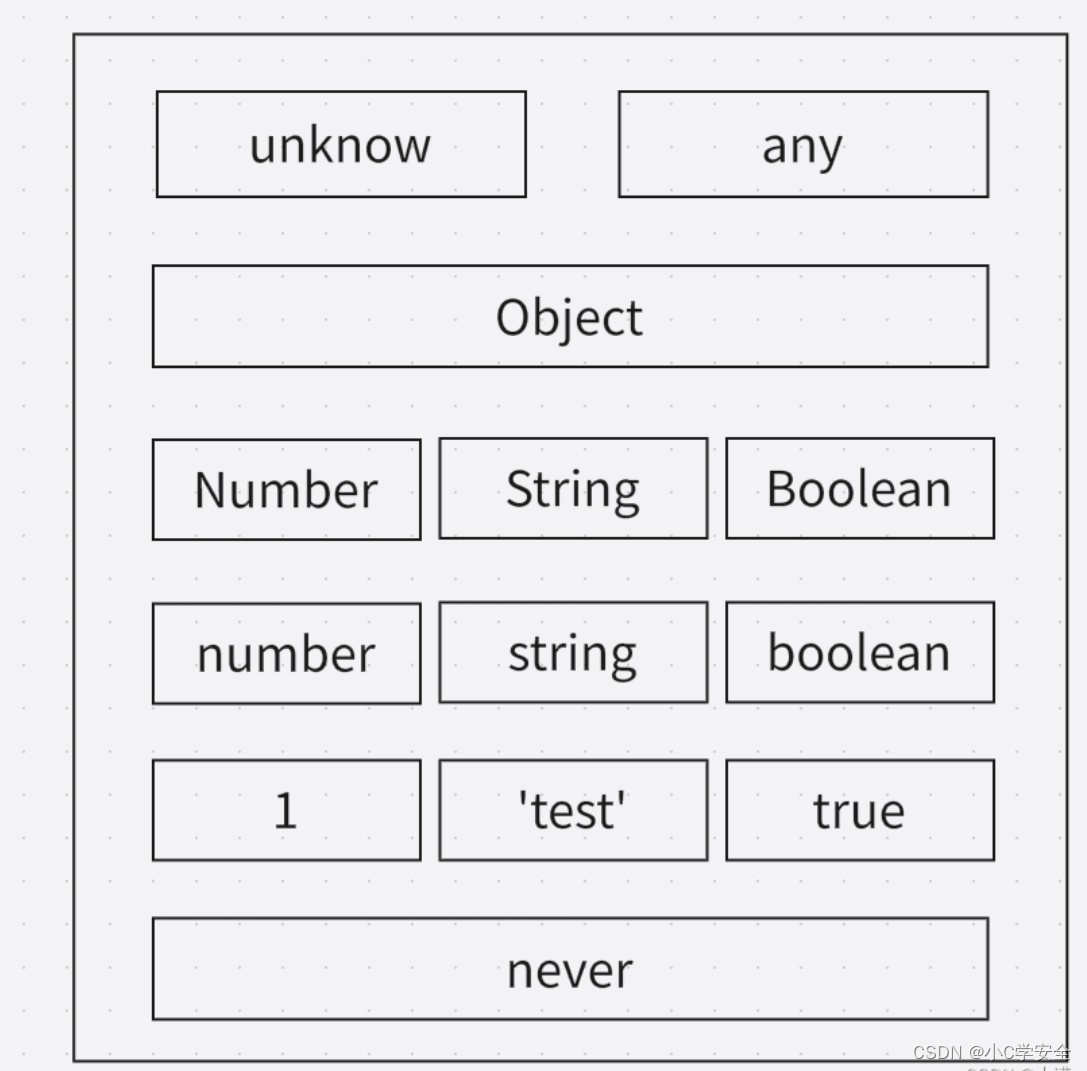
【前端vue3】TypeScrip-类型推论和类型别名
类型推论 TypeScript里,在有些没有明确指出类型的地方,类型推论会帮助提供类型。 例如: 变量xiaoc被推断类型为string 如重新给xiaoc赋值数字会报错 let xiaoc "xiaoc"xiaoc 1111111111111如没有给变量指定类型和赋值…...

javaEE——Servlet
1.web开发概述 所谓web开发,指的是从网页中向后端程序发送请求,与后端程序进行交互 2.java后端开发环境搭建 web后端(javaEE)程序需要运行在服务器中的,这样前端才可以访问得到 3.服务器是什么? ①服务器就是一款软件,可以向其发送请求&#…...
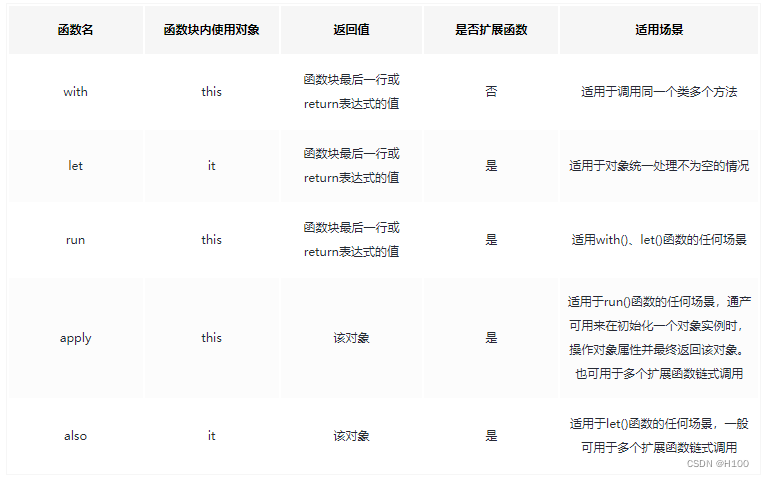
Kotlin扩展函数(also apply run let)和with函数
also apply run let with的使用例子 private fun testOperator() {/*** also*/val person Person("ZhangSan", 18)person.also {// 通常仅仅打印使用, 也可以通过it修改it.name "ZhangSan1"println("also inner name: " it.name)}println(&qu…...

C语言笔记27 •单链表介绍•
1.链表的概念及结构 链表是⼀种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表 中的指针链接次序实现的。 2. 顺序表带来的问题 (1)中间/头部的插⼊删除,时间复杂度为O(N) (2)增容需要申请新空间,拷⻉数据ÿ…...
C++编程(五)单例模式 友元
文章目录 一、单例模式(一)概念(二)实现方式1. 饿汉式2. 懒汉式 二、友元(一)概念(二)友元函数1.概念2.语法格式3. 使用示例访问静态成员变量访问非静态成员变量 (三&…...

012-GeoGebra基础篇-构造圆的切线
前边文章对于基础内容已经悉数覆盖了,这一篇我就不放具体的细节,若有需要可以复刻一下 目录 一、成品展示二、算式内容三、正确性检查五、文章最后 一、成品展示 二、算式内容 A(0,0) B(3,0) c: Circle(A,B) C(5,4) sSegment(A,C) DMidpoint(s) d: Circ…...
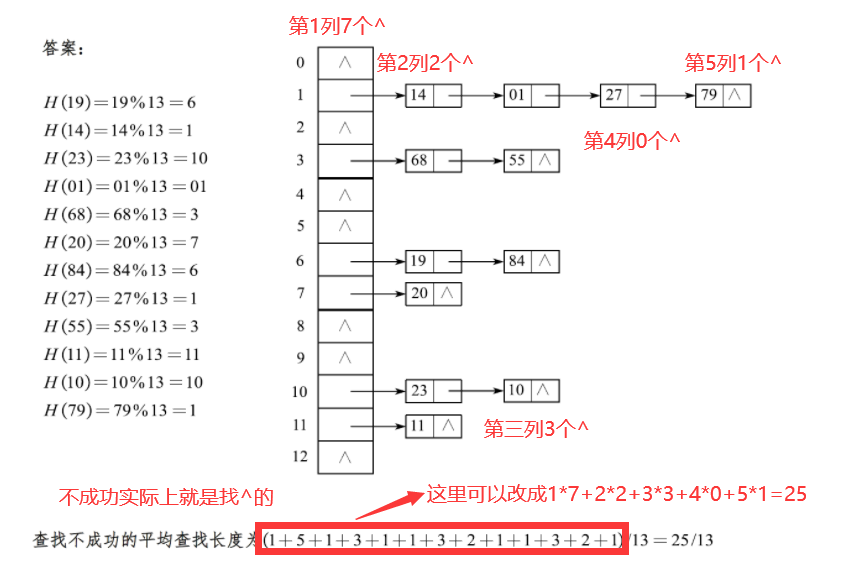
数据结构速成--查找
由于是速成专题,因此内容不会十分全面,只会涵盖考试重点,各学校课程要求不同 ,大家可以按照考纲复习,不全面的内容,可以看一下小编主页数据结构初阶的内容,找到对应专题详细学习一下。 目录 …...
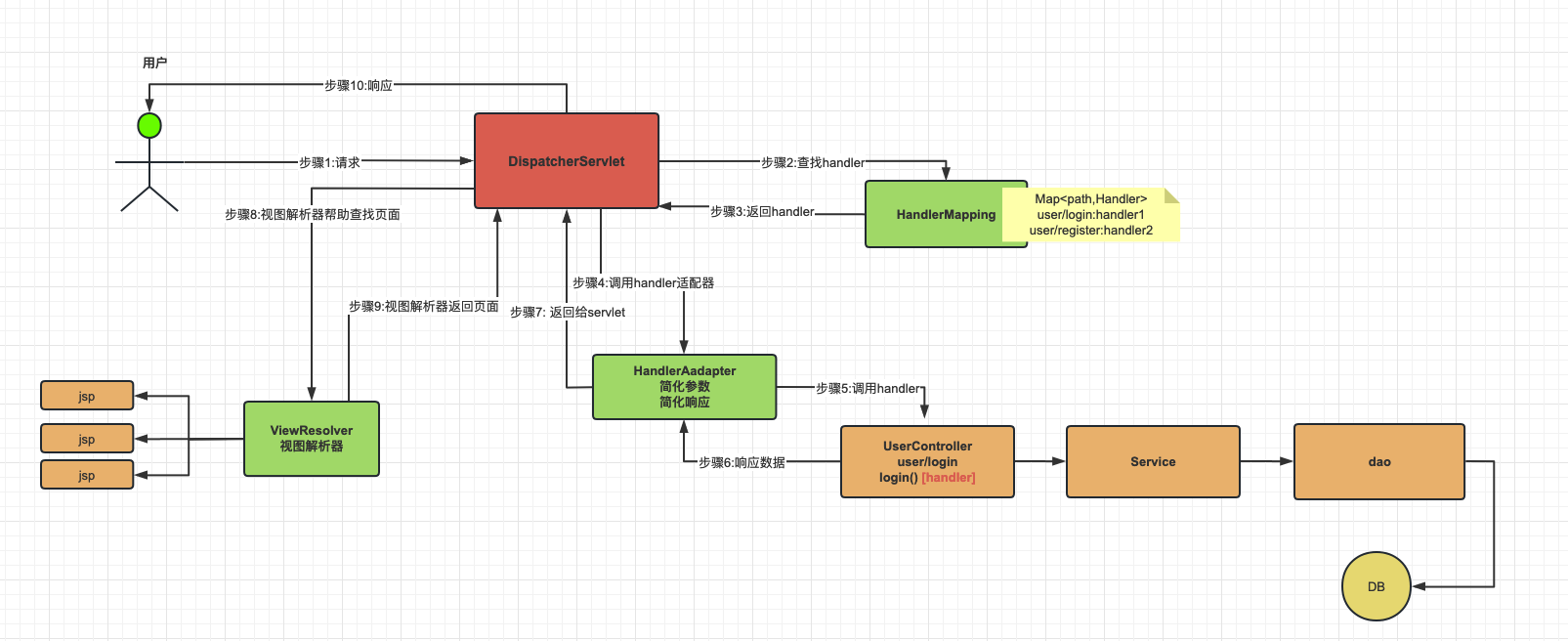
SpringMVC的基本使用
SpringMVC简介 SpringMVC是Spring提供的一套建立在Servlet基础上,基于MVC模式的web解决方案 SpringMVC核心组件 DispatcherServlet:前置控制器,来自客户端的所有请求都经由DispatcherServlet进行处理和分发Handler:处理器&…...
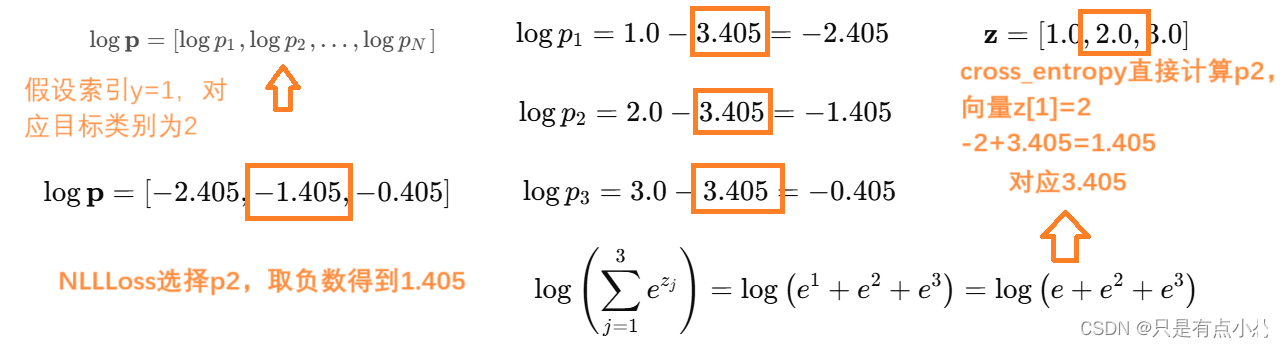
【PYG】Cora数据集分类任务计算损失,cross_entropy为什么不能直接替换成mse_loss
cross_entropy计算误差方式,输入向量z为[1,2,3],预测y为[1],选择数为2,计算出一大坨e的式子为3.405,再用-23.405计算得到1.405MSE计算误差方式,输入z为[1,2,3],预测向量应该是[1,0,0]࿰…...
MyBatis-plus这么好用,不允许还有人不会
你好呀,我是 javapub. 做 Java 的同学都会用到的三件套,Spring、SpringMV、MyBatis。但是由于使用起来配置较多,依赖冲突频发。所有,各路大佬又在这上边做了包装,像我们常用的 SpringBoot、MyBatisPlus。 基于当前要…...

Linux驱动开发实战宝典:设备模型、模块编程、I2C/SPI/USB外设精讲
摘要: 本文将带你走进 Linux 驱动开发的世界,从设备驱动模型、内核模块开发基础开始,逐步深入 I2C、SPI、USB 等常用外设的驱动编写,结合实际案例,助你掌握 Linux 驱动开发技能。 关键词: Linux 驱动,设备驱动模型,内核模块,I2C,SPI,USB 一、Linux 设备驱动模型 Li…...
安全技术和防火墙
1、安全技术 1.1入侵检测系统 特点是不阻断网络访问,主要提供报警和事后监督。不主动介入,默默的看着你(类似于监控) 1.2入侵防御系统 透明模式工作, 数据包,网络监控,服务攻击,…...
Webpack: 开发 PWA、Node、Electron 应用
概述 毋庸置疑,对前端开发者而言,当下正是一个日升月恒的美好时代!在久远的过去,Web 页面的开发技术链条非常原始而粗糙,那时候的 JavaScript 更多用来点缀 Web 页面交互而不是用来构建一个完整的应用。直到 2009年5月…...

python处理txt文件, 如果第一列和第二列的值在连续的行中重复,则只保留一行
处理txt文件, 如果第一列和第二列的值在连续的行中重复,则只保留一个实例,使用Python的内置函数来读取文件,并逐行检查和处理数据。 一个txt文件,里面的数据是893.554382324,-119.955825806,0.0299997832626,-0.133618548512,28.1155740884,112.876833236,46.7922,19.62582…...

C++17中引入了什么新的重要特性
C17是C标准的一个重要版本,它在语言核心和标准库中引入了许多新特性和改进,使得C编程更加现代化和高效。以下是C17中引入的一些重要新特性: 语言核心新特性 结构化绑定(Structured Bindings): 结构化绑定…...

Andrej Karpathy提出未来计算机2.0构想: 完全由神经网络驱动!网友炸锅了
昨天凌晨,知名人工智能专家、OpenAI的联合创始人Andrej Karpathy提出了一个革命性的未来计算机的构想:完全由神经网络驱动的计算机,不再依赖传统的软件代码。 嗯,这是什么意思?全部原生LLM硬件设备的意思吗?…...
)
用国内镜像安装docker 和 docker-compose (ubuntu)
替代方案,改用国内的镜像站(网易镜像) 1.清除旧版本(可选操作) for pkg in docker.io docker-doc docker-compose podman-docker containerd runc; do apt-get remove $pkg; done 2.安装docker apt-get update 首先安装依赖 apt-g…...
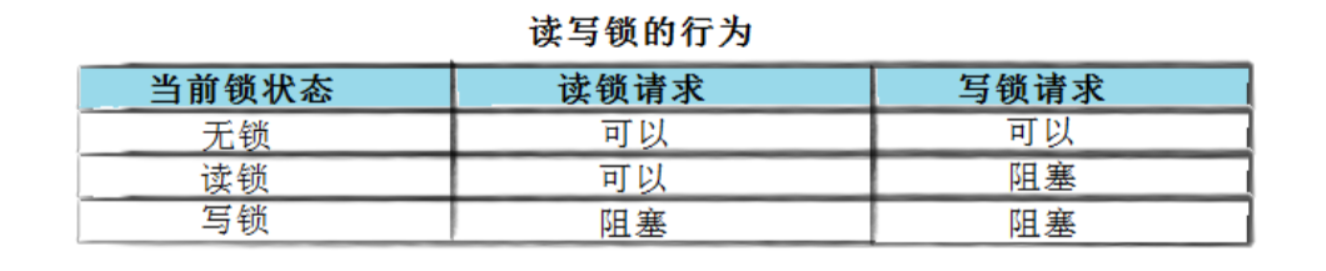
Linux多线程【线程互斥】
文章目录 Linux线程互斥进程线程间的互斥相关背景概念互斥量mutex模拟抢票代码 互斥量的接口初始化互斥量销毁互斥量互斥量加锁和解锁改进模拟抢票代码(加锁)小结对锁封装 lockGuard.hpp 互斥量实现原理探究可重入VS线程安全概念常见的线程不安全的情况常…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...










