Codeforces Round 954 (Div. 3)(A~E)
目录
A. X Axis
B. Matrix Stabilization
C. Update Queries
D. Mathematical Problem
A. X Axis
Problem - A - Codeforces

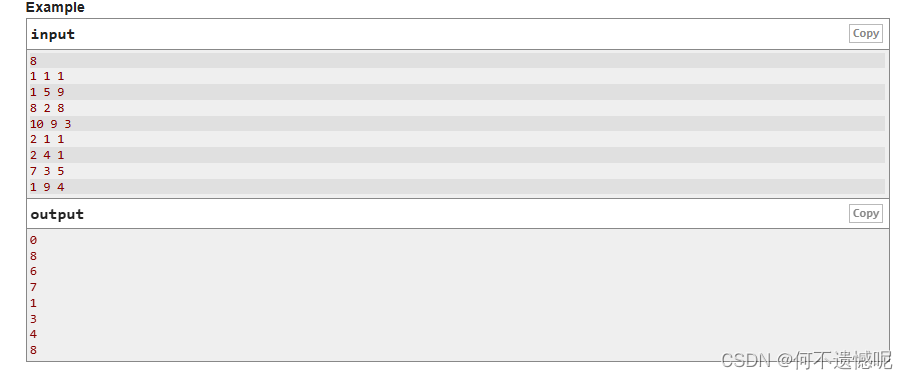
直接找到第二大的数,答案就是这个数与其他两个数的差值的和。
void solve()
{vector<ll>a;for (int i = 1; i <= 3; i++){int x;cin >> x;a.push_back(x);}sort(a.begin(), a.end());cout << a[2]-a[1]+a[1]-a[0] << "\n";}B. Matrix Stabilization
Problem - B - Codeforces

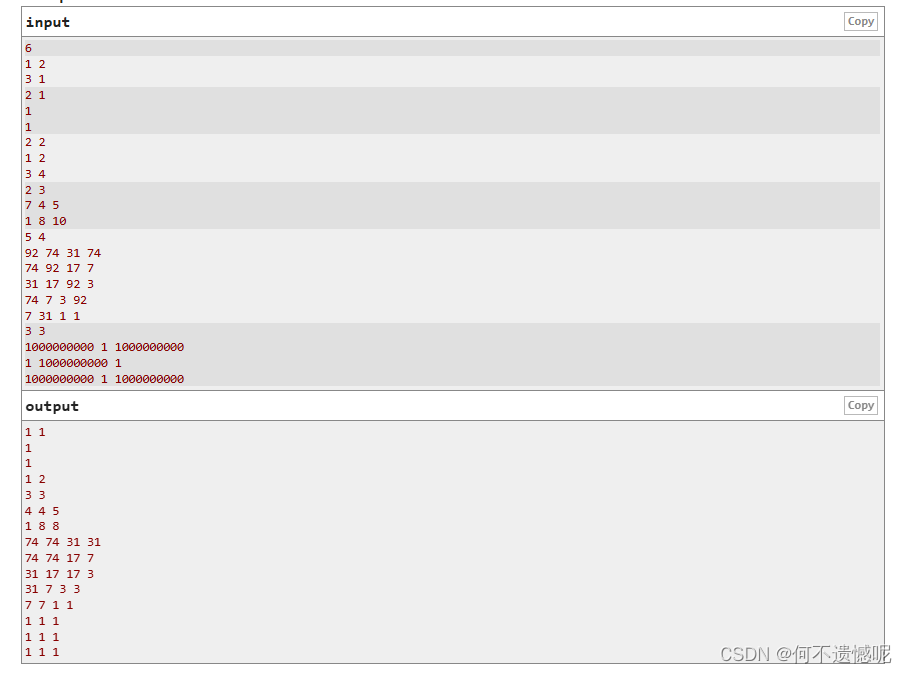
我们发现符合题意的每个数是互不影响的,即改变了其中一个不会影响到另一个,直接找到所以符合题意的数,再将这个数变成周围数的最大值。
int MX(int a, int b, int c, int d)
{vector<int>q;q.push_back(a);q.push_back(b);q.push_back(c);q.push_back(d);sort(q.begin(), q.end());return q[3];
}
void solve()
{memset(f, 0, sizeof(f));int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> f[i][j];}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (f[i][j] > f[i - 1][j] && f[i][j] > f[i][j - 1] && f[i][j] > f[i + 1][j] && f[i][j] > f[i][j + 1]){f[i][j] = MX(f[i - 1][j], f[i + 1][j], f[i][j - 1], f[i][j + 1]);}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cout<< f[i][j]<<" ";}cout << "\n";}cout << "\n";
}C. Update Queries
Problem - C - Codeforces


仔细看就会发现这个操作数组顺序其实没多大关系,只要找到需要操作的所以,再一次填入已经排好序的元素即可。
ll d[200010];
void solve()
{memset(d, 0, sizeof(d));ll n, m;cin >> n >> m;string s1, s2;cin >> s1;int x;for (int i = 1; i <= m; i++) cin >> x, d[x]++;cin >> s2;sort(s2.begin(), s2.end());int c = 0;for (int i = 0; i < s1.size(); i++){if (d[i + 1]&&c<s2.size()){s1[i] = s2[c++];}}cout << s1 << "\n";
}D. Mathematical Problem
Problem - D - Codeforces
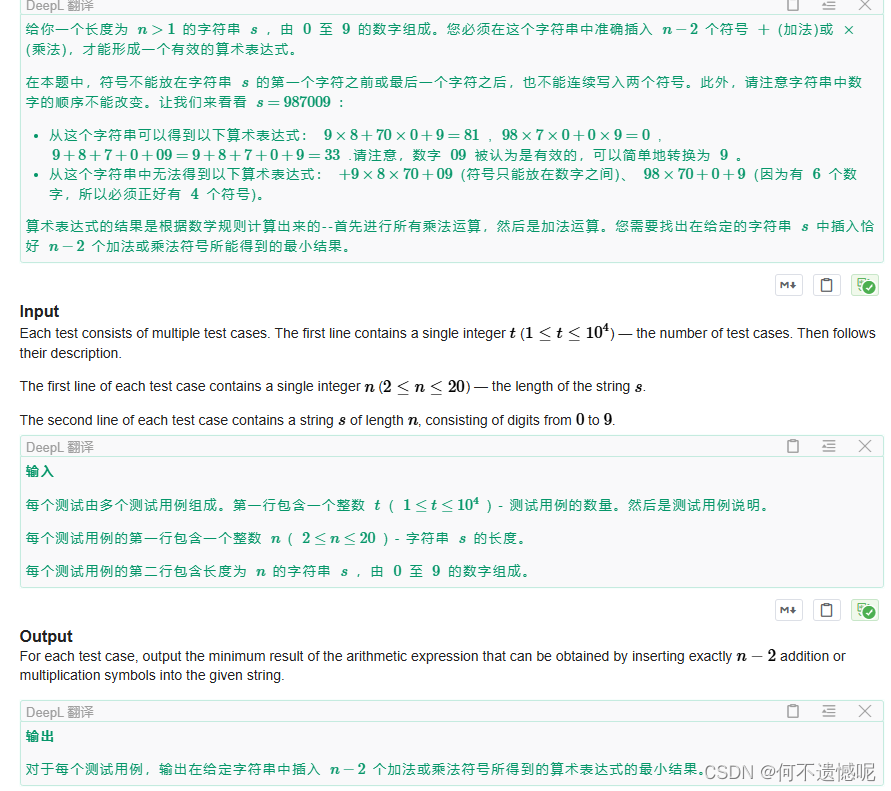
考虑n大于2的情况
当含有元素0时,那么答案就是0,因为可以将他们全部相乘。
当所以元素都为1时,答案就是1,可以全部相乘。
其他情况,答案就是不为1的所有元素的和。
void solve()
{int n;cin >> n;string s;cin >> s;vector<int> cnt(10);int sum = 0;for (int i = 1; i < n; i++) {if (s[i] <= '1') {cnt[s[i] - '0']++;}sum += s[i] - '0';}constexpr int inf = 1e9;int ans = inf;for (int i = 0; i + 2 <= n; i++) {cnt[s[i + 1] - '0']--;sum -= s[i + 1] - '0';int x = stoi(s.substr(i, 2));cout << x << ' ' << sum << ' ' << cnt[0] << ' ' << cnt[1] << '\n';int res;if (cnt[0] + (x == 0) > 0) {res = 0;}else if (cnt[1] + (x == 1) == n - 1) {res = 1;}else {res = (x != 1 ? x : 0) + sum - cnt[1];}ans = min(ans, res);cnt[s[i] - '0']++;sum += s[i] - '0';}cout << ans << '\n';
}相关文章:

Codeforces Round 954 (Div. 3)(A~E)
目录 A. X Axis B. Matrix Stabilization C. Update Queries D. Mathematical Problem A. X Axis Problem - A - Codeforces 直接找到第二大的数,答案就是这个数与其他两个数的差值的和。 void solve() {vector<ll>a;for (int i 1; i < 3; i){int x;…...
基于Java微信小程序同城家政服务系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟感兴趣的可以先收藏起来,还…...
[21] Opencv_CUDA应用之使用Haar级联的对象检测
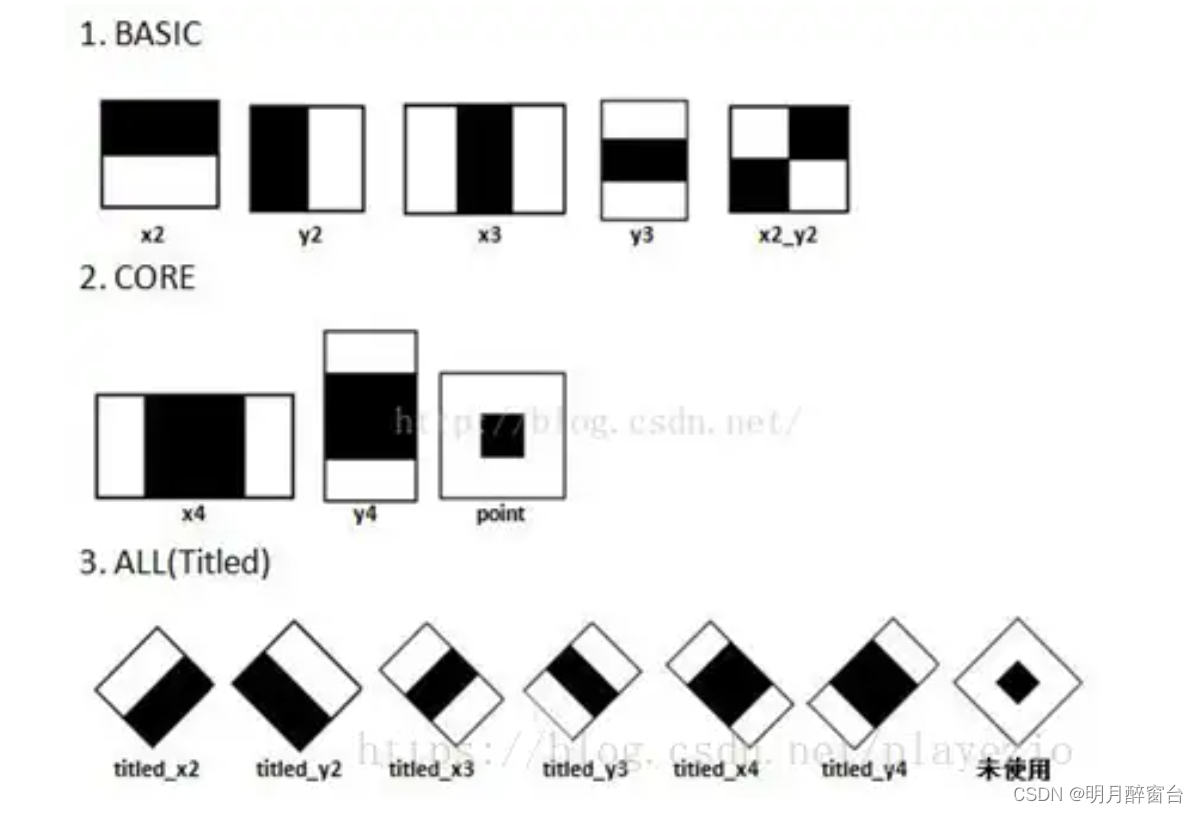
Opencv_CUDA应用之使用Haar级联的对象检测 Haar级联使用矩形特征来检测对象,它使用不同大小的矩形来计算不同的线和边缘特征。矩形包含一些黑色和白色区域,如下图所示,它们在图像的不同位置居中 类Haar特征检测算法的思想是计算矩形内白色像素和黑色像素之间的差异这个方法的…...
CXL:拯救NVMe SSD缓存不足设计难题-2
LMB提出了基于CXL协议的内存扩展框架和内核模块。该方案利用CXL内存扩展器作为物理DRAM源,旨在提供一个统一的内存分配接口,使PCIe和CXL设备都能方便地访问扩展的内存资源。通过这个接口,NVMe驱动和CUDA的统一内存内核驱动可以直接高效地访问…...

Opencv学习项目6——pyzbar
在之前我们学习了解码图片中的二维码,这次我们开启摄像头来解码视频中二维码 开启摄像头 # 打开摄像头 cap cv2.VideoCapture(0) cap.set(3, 640) # 设置摄像头画面宽度 cap.set(4, 480) # 设置摄像头画面高度 我使用的是笔记本上的摄像头来进行的,…...
 大气层双系统图文教程)
Switch 刷安卓11 (LineageOS 18.1) 大气层双系统图文教程
很多朋友手上已经拥有了完成硬破的 Switch ,但又不甘心仅仅使用 Switch 本身的地平线系统,Switch 刷安卓 (Android 11) 会是一个好的选择,虽然 Switch 的 CPU 性能拉跨,但和桌面平台同一设计思路的TegraX1 GPU 可谓是先于时代&…...

Spring Boot与Spring Batch的深度集成
Spring Boot与Spring Batch的深度集成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨在Spring Boot应用中如何实现与Spring Batch的深度集成…...
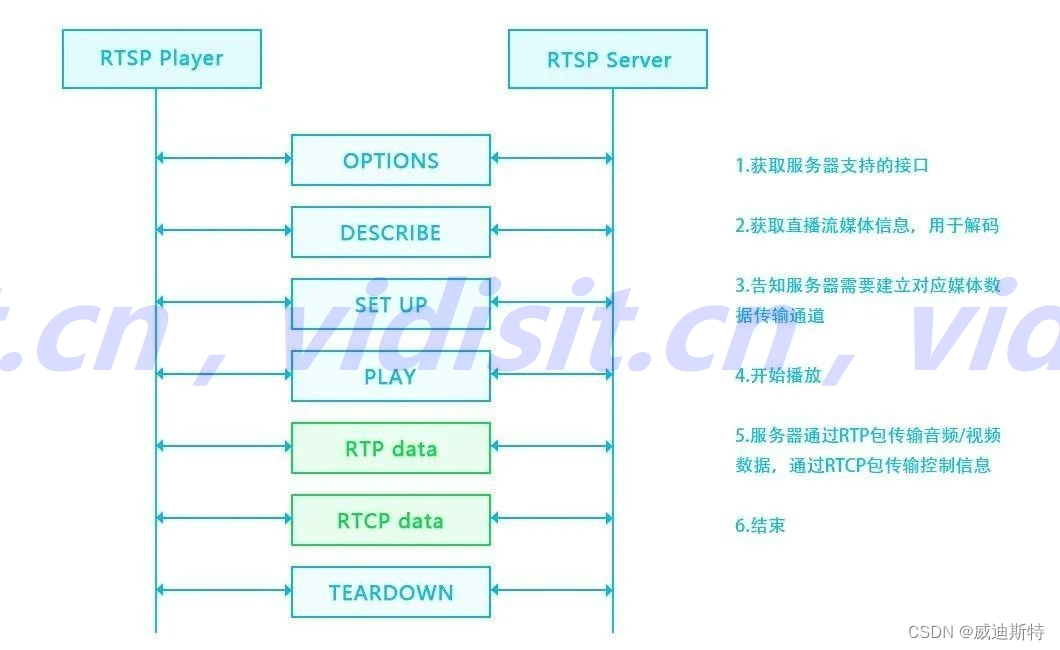
RTSP协议在视频监控系统中的典型应用、以及视频监控设备的rtsp地址格式介绍
目录 一、协议概述 1、定义 2、提交者 3、位置 二、主要特点 1、实时性 2、可扩展性 3、控制功能 4、回放支持 5、网络适应性 三、RTSP的工作原理 1、会话准备 2、会话建立 3、媒体流控制 4、会话终止 5、媒体数据传输 四、协议功能 1、双向性 2、带外协议 …...

Kotlin基础——异步和并发
同步和异步 同步指的是一种行为:当执行IO操作的时候,在代码层面上我们需要主动去等待结果,直到结果返回阻塞指的是一种状态:当执行IO操作的时候,线程处于挂起状态,就是该线程没有执行了 故同步不是阻塞&a…...

消防认证-防火卷帘
一、消防认证 消防认证是指消防产品符合国家相关技术要求和标准,且通过了国家认证认可监督管理委员会审批,获得消防认证资质的认证机构颁发的证书,消防产品具有完好的防火功能,是住房和城乡建设领域验收的重要指标。 二、认证依据…...

SpringBoot3.3集成knif4j-swagger文档方式和使用案例
springboot3 集成 knif4j : 访问地址: swagger 接口文档默认地址:http://localhost:8080/swagger-ui.html# Knife4j 接口文档默认地址:http://127.0.0.1:8080/doc.html Maven: <dependency><groupId>com.github.x…...

老年服务与管理实训室:制定教学模式
随着我国人口老龄化程度的加深,如何为老年人提供优质的养老服务成为社会关注的重点。作为培养老年服务人才的重要阵地,老年服务与管理实训室应制定科学合理的教学模式,满足行业发展需求,培养出高素质的老年服务专业人才。本文针对老年服务与管理实训室的教学模式展开探讨,提出相…...

4、DDD、中台和微服务的关系
DDD、中台和微服务的关系 1 DDD和中台的本质 领域驱动设计(DDD)和中台在企业架构中有着密切的关系。DDD的本质在于通过对业务领域的深入分析和建模,构建高内聚、低耦合的系统。而中台则是对企业核心业务能力的抽象和封装,以实现…...

【ACM出版,马来西亚-吉隆坡举行】第四届互联网技术与教育信息化国际会议 (ITEI 2024)
作为全球科技创新大趋势的引领者,中国不断营造更加开放的科技创新环境,不断提升学术合作的深度和广度,构建惠及各方的创新共同体。这是对全球化的新贡献,是构建人类命运共同体的新贡献。 第四届互联网技术与教育信息化国际学术会议…...

走进IT的世界
引言 随着高考的结束,对于即将踏入IT(信息技术)领域的新生而言,这个假期不仅是放松身心的时间,更是提前规划、深化专业知识、为大学生活奠定坚实基础的宝贵机会。以下是一份详尽的高考假期预习与规划指南,…...

Linux 时区文件编译器 zic【man 8 zic】
1. NAME(名) zic - 时区编译器 2. SYNOPSIS(概要) zic [-v] [-d directory] [-l localtime] [-p posixrules] [-L leapsecondfilename] [-s] [-y command] [filename ...]3. DESCRIPTION(函数描述) zic…...

Springboot下使用Redis管道(pipeline)进行批量操作
之前有业务场景需要批量插入数据到Redis中,做的过程中也有一些感悟,因此记录下来,以防忘记。下面的内容会涉及到 分别使用for、管道处理批量操作,比较其所花费时间。 分别使用RedisCallback、SessionCallback进行Redis pipeline …...

Vue技巧大揭秘:自定义指令的力量与应用
引言 自定义指令就像是给予开发者的一把魔法钥匙,它能够打开DOM操作的新世界,按我的理解就是把对DOM操作的逻辑进行封装 全局注册与局部注册 全局注册 定义: 全局注册意味着自定义指令在Vue实例创建之前通过Vue.directive()方法注册&…...

HR人才测评,如何考察想象力?
什么是想象力? 想象力是指,人们通过在已有物质的基础上,通过大脑想象、加工、创造出新事物的能力,举一个非常简单的例子,在提到鸟这种生活的时候,大家会联想到各种各样不同鸟的品种。 在企业招聘中常常应…...

Git命令远程分支的合并和本地分支的同步
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
