sklearn降维算法1 - 降维思想与PCA实现
目录
- 1、概述
- 1.1 维度概念
- 2、PCA与SVD
- 2.1 降维实现
- 2.2 重要参数n_components
- 2.2.1 案例:高维数据的可视化
- 2.2.2 最大似然估计自选超参数
- 2.2.3 按信息量占比选超参数
1、概述
1.1 维度概念
shape返回的结果,几维几个方括号嵌套

特征矩阵特指二维的
一般来说,维度指的是样本的数量或特征的数量
降维算法,指降低特征矩阵中特征的数量。降维是为了让算法运算能更快,效果更好,但还有一种需求:数据可视化(三维以上的无法可视化)
sklearn中降维算法被包括在模块decomposition中,这是一个矩阵分解模块

SVD和主成分分析PCA属于矩阵分解算法中的入门算法,都是通过分解特征矩阵来降维。
2、PCA与SVD
特征选择方法:方差过滤。
如果一个特征的方差很小,则意味着这个特征上很可能有大量取值都相同(比如90%都是1,只有10%是0,甚至100%是1),那这一个特征的取值对样本而言就没有区分度,这种特征就不带有有效信息。从方差的这种应用就可以推断出,如果一个特征的方差很大,则说明这个特征上带有大量的信息。
因此,在降维中,PCA使用的信息量衡量指标,就是样本方差,又称可解释性方差,方差越大,特征所带的信息量越多。

问:方差计算公式中为什么除数是n-1?
答:这是为了得到样本方差的无偏估计
2.1 降维实现
sklearn.decomposition.PCA
举一个栗子:
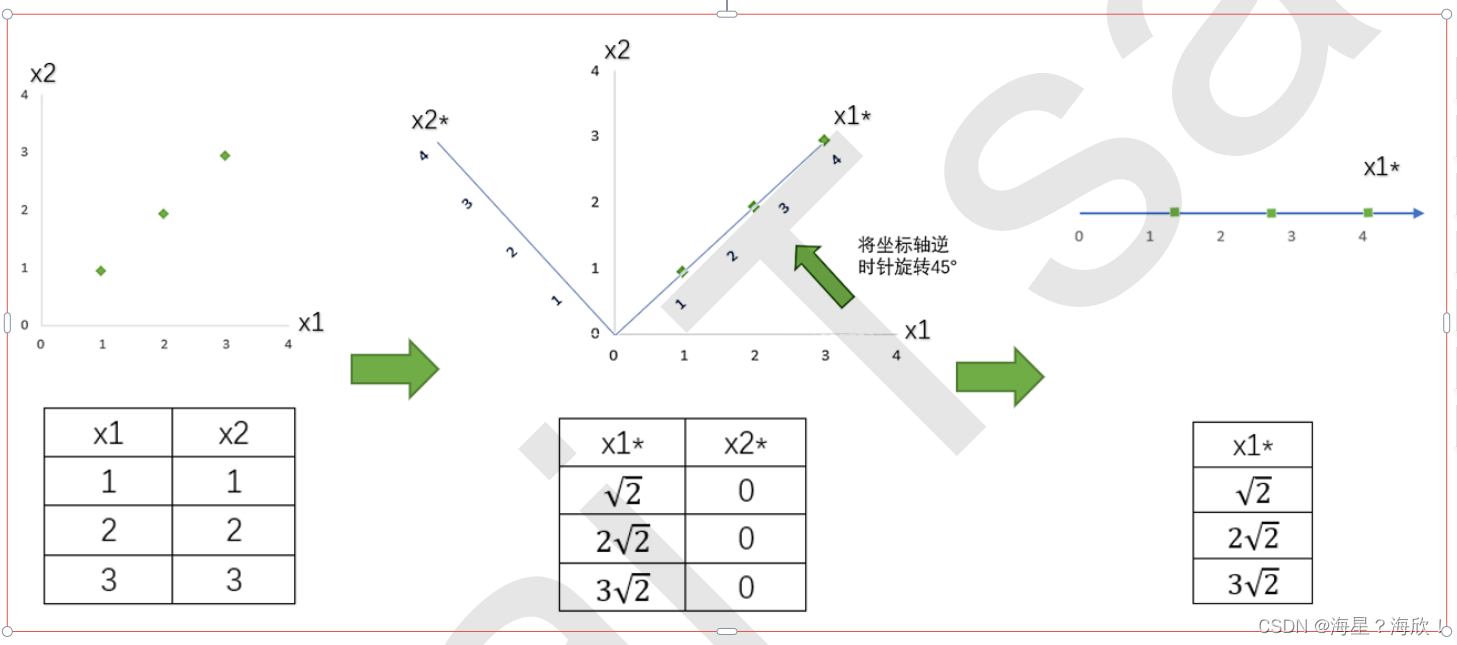
原数据,特征x1和x2,三个样本点,在二维平面中可以作图出来,现在每个数据特征的均值是2,方差计算出来为1
目标:进行降维,只用一个一个特征向量来描述这组数据,即将二维数据降为一维数据,并且尽可能地保留信息量,即让数据的总方差尽量靠近2。于是,我们将原本的直角坐标系逆时针旋转45°,形成了新的特征向量x1和x2组
新数据:x2上的数值此时都变成了0,因此x2明显不带有任何有效信息了(此时x2的方差也为0了)。此时,x1特征上方差为2
结果:根据信息含量的排序,取信息含量最大的一个特征,因为我们想要的是一维数据。所以我们可以将x2删除,同时也删除图中的x2特征向量,剩下的x1*就代表了曾经需要两个特征来代表的三个样本点。
通过旋转原有特征向量组成的坐标轴来找到新特征向量和新坐标平面,我们将三个样本点的信息压缩到了一条直线上,实现了二维变一维,并且尽量保留原始数据的信息。一个成功的降维,就实现了。
将二维特征矩阵进行推广:
二维特征矩阵:
- 输入原数据,结构为 (3,2) 找出原本的2个特征对应的直角坐标系,本质是找出这2个特征构成的2维平面
- 决定降维后的特征数量:1
- 旋转,找出一个新坐标系。新特征向量让数据能够被压缩到少数特征上,并且总信息量不损失太多
- 找出数据点在新坐标系上,2个新坐标轴上的坐标
- 选取第1个方差最大的特征向量,删掉没有被选中的特征,成功将2维平面降为1维
n维特征矩阵:
- 输入原数据,结构为 (m,n) 找出原本的n个特征向量构成的n维空间V
- 决定降维后的特征数量:k
- 通过某种变化,找出n个新的特征向量,以及它们构成的新n维空间V
- 找出原始数据在新特征空间V中的n个新特征向量上对应的值,即“将数据映射到新空间中”
- 选取前k个信息量最大的特征,删掉没有被选中的特征,成功将n维空间V降为k维
五步骤:原数据特征 - 降维数 - 变换成新特征空间 - 数据映射到新空间 - 按信息量排序,取前k个
步骤3中,变化找到新特征向量,让数据能够被压缩到少数特征上并且总信息量不损失太多的技术就是矩阵分解。
PCA和SVD比较
PCA和SVD是两种不同的降维算法,但他们都遵从上面的过程来实现降维,只是两种算法中矩阵分解的方法不同,信息量的衡量指标不同罢了。
PCA使用方差作为信息量的衡量指标,并且特征值分解来找出空间V。降维完成之后,PCA找到的每个新特征向量就叫做“主成分”,而被丢弃的特征向量被认为信息量很少,这些信息很可能就是噪音。
而SVD使用奇异值分解来找出空间V,其中Σ也是一个对角矩阵,不过它对角线上的元素是奇异值
问题:
无论是PCA和SVD都需要遍历所有的特征和样本来计算信息量指标。并且在矩阵分解的过程之中,会产生比原来的特征矩阵更大的矩阵
无论是Python还是R,或者其他的任何语言,在大型矩阵运算上都不是特别擅长,无论代码如何简化,我们不可避免地要等待计算机去完成这个非常庞大的数学计算过程。因此,降维算法的计算量很大,运行比较缓慢,但无论如何,它们的功能无可替代
PCA和特征选择都是特征工程的一部分,两者区别?
答:特征工程中有三种方式:特征提取,特征创造和特征选择。
特征选择是从已存在的特征中选取携带信息最多的,选完之后的特征依然具有可解释性,我们依然知道这个特征在原数据的哪个位置,代表着原数据上的什么含义。
而PCA,是将已存在的特征进行压缩,降维完毕后的特征不是原本的特征矩阵中的任何一个特征,而是通过某些方式组合起来的新特征。通常来说,在新的特征矩阵生成之前,我们无法知晓PCA都建立了怎样的新特征向量,新特征矩阵生成之后也不具有可读性,我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而来,新特征虽然带有原始数据的信息,却已经不是原数据上代表着的含义了。以PCA为代表的降维算法因此是特征创造的一种。
PCA一般不适用于探索特征和标签之间的关系的模型(如线性回归),因为无法解释的新特征和标签之间的关系不具有意义。在线性回归模型中,我们使用特征选择。
2.2 重要参数n_components
n_components是我们降维后需要的维度,即降维后需要保留的特征数量K,
[0, min(X.shape)]范围中的整数
问题:
如果留下的特征太多,就达不到降维的效果,如果留下的特征太少,那新特征向量可能无法容纳原始数据集中的大部分信息,因此,n_components既不能太大也不能太小
解决:如果降维目标是可视化,希望可视化一组数据来观察数据分布,我们往往将数据降到三维以下,很多时候是二维,即n_components的取值为2。
2.2.1 案例:高维数据的可视化
可视化:至少要降维到3维
1,导模块
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris #鸢尾花数据
from sklearn.decomposition import PCA
2,数据了解
iris = load_iris()
y = iris.target
x = iris.data
x.shape #(150,4)-150条样本,4个特征,4维度
import pandas as pd
pd.DataFrame(x)
y的输出,三种可能
3,降维:
#调用PCA
pca = PCA(n_components=2) #实例化
pca = pca.fit(x) #拟合模型
x_dr = pca.transform(x) #获取新矩阵
x_dr.shape #输出(150,2)降维到了2维#fit_transform一步到位
#x_dr = PCA(2).fit_transform(x)
4,可视化
对于得到的x_dr

x_dr[y==0,0]#取出标签为0的记录的,第一列的数据

plt.figure() #要画图,给一个画布
plt.scatter(x_dr[y==0,0],x_dr[y==0,1],c=c="red", label=iris.target_names[0]) #标签为0的数据,散点图x提供横纵坐标,y表现不同颜色
#iris.target_names特征名字
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()

上面的作图代码,可以用for循环实现一下:
对数据,名字,颜色都循环
colors = ['red','black', 'orange']plt.figure()
foriin [0, 1, 2]:plt.scatter(X_dr[y == i, 0],X_dr[y == i, 1],alpha=.7 #颜色透明度,c=colors[i],label=iris.target_names[i] )
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()鸢尾花数据集,是一个明显的分簇分布。一个有很好效果的数据集
5,探索降维后数据:
explained_variance_,查看降维后每个新特征向量上所带的信息量大小
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)pca.explained_variance_
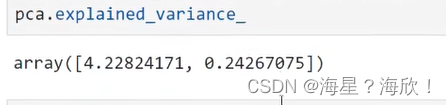
降维后剩下的x1和x2,所以返回了这两个的方差
explained_variance_ratio,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比
#属性explained_variance_ratio,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比#又叫做可解释方差贡献率
pca.explained_variance_ratio_
#大部分信息都被有效地集中在了第一个特征上

结果显示,原始总信息的92%在新特征x1上,原始总信息的5%在新特征x2上
pca.explained_variance_ratio_.sum()
输出97.76%,说明原始信息的97%都留在了新特征上。特征减掉了两个,而信息损失不到3%。–PCA效果好
6,选择最好的n_components:累积可解释方差贡献率曲线
累积可解释方差贡献率曲线是一条以降维后保留的特征个数为横坐标,降维后新特征矩阵捕捉到的可解释方差贡献率为纵坐标的曲线,能够帮助我们决定n_components最好的取值。
当参数n_components中不填写任何值,则默认返回min(X.shape)个特征,可以画出累计可解释方差贡献率曲线
pca_line = PCA().fit(X)
pca_line.explained_variance_ratio_
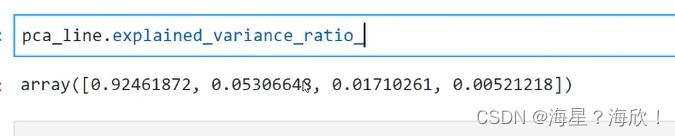
返回的是,每个特征带有的原始信息的占比
import numpy as np
np.cumsum(pca_line.explained_variance_ratio_) #返回的是累加
import numpy as np
pca_line = PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
#上面的[1,2,3,4]是x的取值,不写,会自动写入坐标
plt.xticks([1,2,3,4]) #这是为了限制坐标轴显示为整数
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()
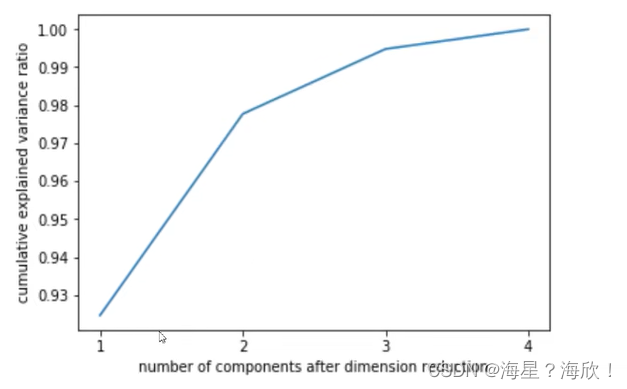
找图像中的转折点
2.2.2 最大似然估计自选超参数
除了输入整数,n_components还有哪些选择呢?
PCA可以用最大似然估计(maximum likelihood estimation)自选超参数的方法,输入“mle”作为n_components的参数输入,就可以调用这种方法。
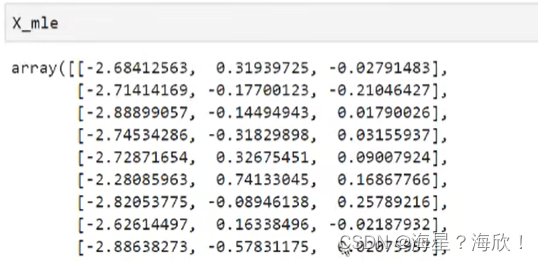
pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)X_mle #自动选择了三列特征
pca_mle.explained_variance_ratio_.sum()
#0.994
#得到了比设定2个特征时更高的信息含量,对于鸢尾花这个很小的数据集来说,3个特征对应这么高的信息含量,并不需要去纠结于只保留2个特征,毕竟三个特征也可以可视化
2.2.3 按信息量占比选超参数
输入[0,1]之间的浮点数,并且让参数svd_solver ==‘full’,表示希望降维后的总解释性方差占比大于n_components 指定的百分比,即是说,希望保留百分之多少的信息量。
比如说,如果我们希望保留97%的信息量,就可以输入
n_components = 0.97,PCA会自动选出能够让保留的信息量超过97%的特征数量。
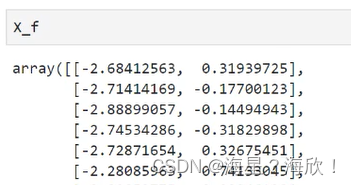
pca_f = PCA(n_components=0.97,svd_solver="full") #帮忙选出总信息占比超过97%的特征
pca_f = pca_f.fit(X)
X_f = pca_f.transform(X)
X_f #自动选择了两维
pca_f.explained_variance_ratio_ #[0.92,0.053]pca_f.explained_variance_ratio_.sum() #0.97
相关文章:

sklearn降维算法1 - 降维思想与PCA实现
目录1、概述1.1 维度概念2、PCA与SVD2.1 降维实现2.2 重要参数n_components2.2.1 案例:高维数据的可视化2.2.2 最大似然估计自选超参数2.2.3 按信息量占比选超参数1、概述 1.1 维度概念 shape返回的结果,几维几个方括号嵌套 特征矩阵特指二维的 一般来…...

「期末复习」线性代数
第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘积全排列与对换逆序数为奇就为奇排列,逆序数为偶就为偶排列对换:定理一:一个排列的任意两个元素对换,排列改变奇偶性(和…...
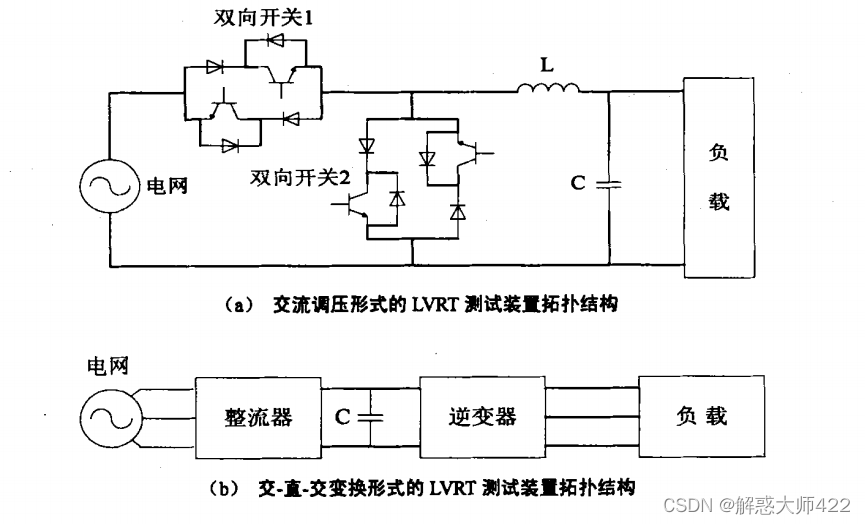
伏并网低电压穿越技术
国内光伏并网低电压穿越要求 略: 低电压穿越方法 当前,光伏电站实现低电压穿越可通过两种方式,即增加硬件设备或者改变控制策略。本节对基于储能设备、基于无功补偿设备、基于无功电流电压支撑控制策略三种实现LVRT的典型方法进行介绍。 …...
opencv的环境搭建
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++智能指针
c11的三个智能指针 unique_ptr独占指针,用的最多 shared_ptr记数指针,其次 weak_ptr,shared_ptr的补充,很少用 引用他们要加上头文件#include unique_ptr独占指针: 1.只能有一个智能指针管理内存 2.当指针超出作用域…...
MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程
目录 数据库简介 MongoDB数据库的安装 MongoDB数据库的启动 MongoDB数据库环境变量的配置 MongoDB图形化管理工具 数据库简介 在使用MongoDB数据库之前,我们应该要知道我们使用它的原因: 在数据库当中,有常见的三高需求: Hi…...

JAVA 基础题
1. 面向对象有哪些特征?答:继承、封装、多态2. JDK与JRE的区别是什么?答:JDK是java开发时所需环境,它包含了Java开发时需要用到的API,JRE是Java的运行时环境,JDK包含了JRE,他们是包含…...

Flutter desktop端多屏幕展示问题处理
目前越来越多的人用Flutter来做桌面程序的开发,很多应用场景在Flutter开发端还不是很成熟,有些场景目前还没有很好的插件来支持,所以落地Flutter桌面版还是要慎重。 下面来说一下近期我遇到的一个问题,之前遇到一个需要双屏展示的…...

每天10个前端小知识 【Day 9】
👩 个人主页:不爱吃糖的程序媛 🙋♂️ 作者简介:前端领域新星创作者、CSDN内容合伙人,专注于前端各领域技术,成长的路上共同学习共同进步,一起加油呀! ✨系列专栏:前端…...

Elasticsearch的读写搜索过程
问题 Elasticsearch在读写数据的过程是什么样的?你该如何理解这个问题! Elasticsearch的写数据过程 客户端选择一个节点发送请求,这个时候我们所说的这个节点就是协调节点(coordinating node)协调节点对document进行了路由&am…...

线上服务质量的问题该如何去处理?你有什么思路?
线上服务质量的问题该如何去处理?你有什么思路? 目录:导读 发现线上故障 处理线上故障 修复线上故障 运营线上质量 就是前几天有个同学问了我一个问题:目前业内高可用部署主要采用方案? 看到这个问题,…...

IOC 配置,依赖注入的三种方式
xml 配置 顾名思义,就是将bean的信息配置.xml文件里,通过Spring加载文件为我们创建bean。这种方式出现很多早前的SSM项目中,将第三方类库或者一些配置工具类都以这种方式进行配置,主要原因是由于第三方类不支持Spring注解。 优点…...
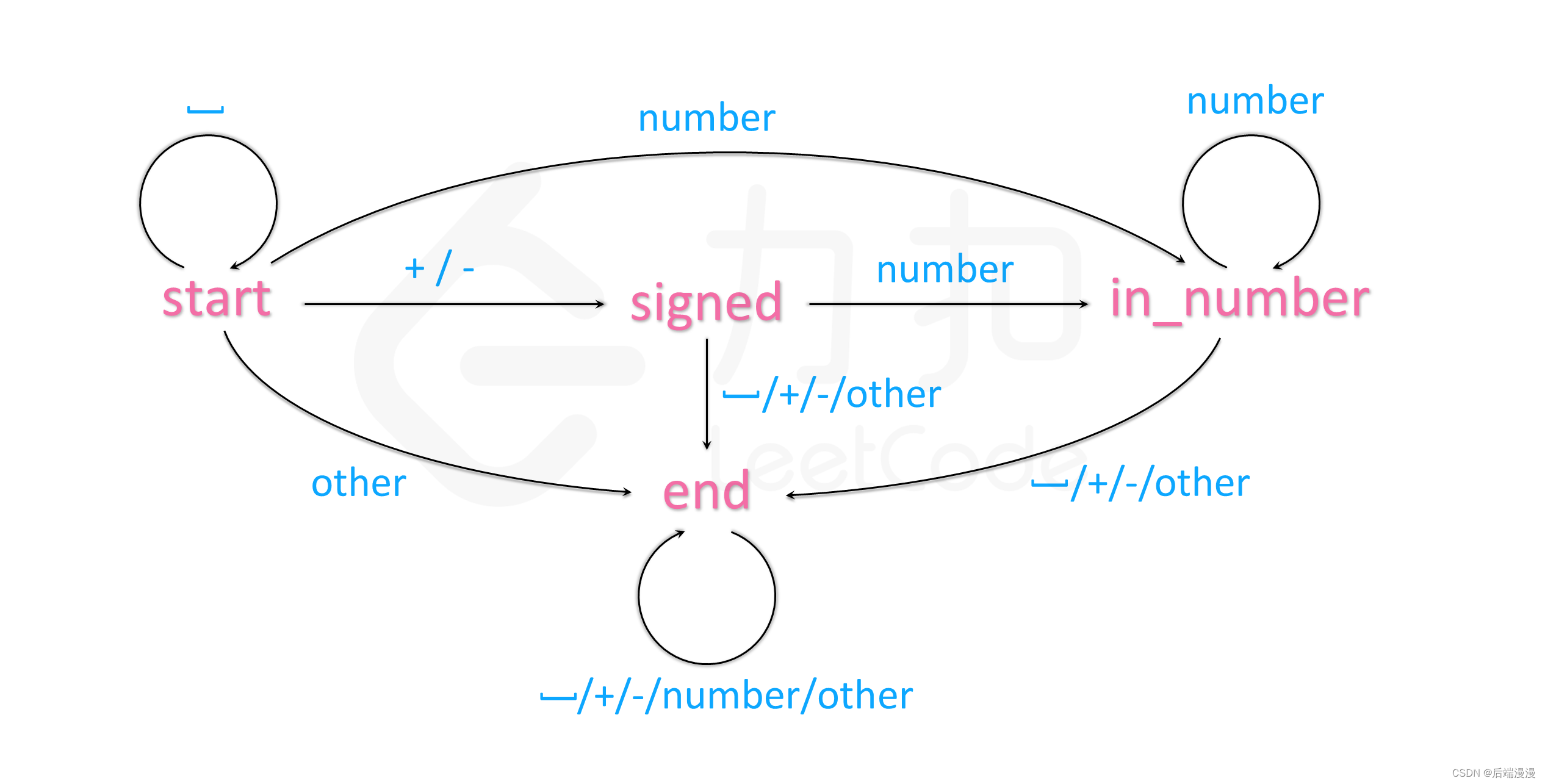
自动机,即有限状态机
文章目录一、问题来源二、题目描述三、题解中的自动机四、自动机学习五、有限状态机的使用场景一、问题来源 今天做力克题目的时候看到了字符串转换整数的一道算法题,其中又看到了题解中有自动机的概念,所以在这里对自动机做个笔记。题目链接 二、题目描…...
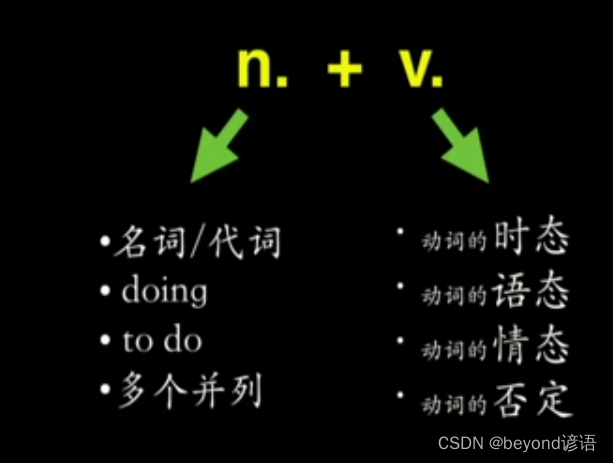
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(主语/宾语/表语的变化)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

VSCode Markdown写作引入符合规范的参考文献
Markdown可以用来写论文,写论文的时候无一例外要用到参考文献,今天来谈谈怎么自动生成参考文献。之前讲了怎么导出的pdf,文章在这里 VSCode vscode-pandoc插件将中文Markdown转换为好看的pdf文档(使用eisvogel模板) …...
电子学会2022年12月青少年软件编程(图形化)等级考试试卷(四级)答案解析
目录 一、单选题(共15题,共30分) 二、判断题(共10题,共20分) 三、编程题(共3题,共50分) 青少年软件编程(图形化)等级考试试卷(四级) 一、单选题(共15题,共30分) 1. 运行下列程序…...

JUC并发编程学习笔记(一)——知识补充(Threadlocal和引用类型)
强引用、弱引用、软引用、虚引用 Java执行 GC(垃圾回收)判断对象是否存活有两种方式,分别是引用计数法和引用链法(可达性分析法)。 **引用计数:**Java堆中给每个对象都有一个引用计数器,每当某个对象在其它地方被引用时,该对象的…...

2022级上岸浙理工MBA的复试经验提炼和备考建议
在等待联考成绩出来的那段时间,虽然内心很忐忑,但还是为复试在积极的做准备,虽然也进行了估分大概有201分,但成绩和分数线没下来之前,只能尽量多做些一些准备把。因为笔试报了达立易考的辅导班,对于浙江理工…...

人大金仓数据库索引的应用与日常运维
索引的应用 一、常见索引及适应场景 BTREE索引 是KES默认索引,采用B树实现。 适用场景 范围查询和优化排序操作。 不支持特别长的字段。 HASH索引 先对索引列计算一个散列值(类似md5、sha1、crc32),然后对这个散列值以顺序…...

20230211英语学习
Six Lifestyle Choices to Slow Memory Decline 研究发现,生活方式真能帮助记忆“抗衰”? A combination of healthy lifestyle choices such as eating well, regularly exercising, playing cards and socialising at least twice a week may help sl…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
