Java源码解读之常量52429
文章目录
- 为什么有52429的常量呢?
- 对于为什么选择52429?
- 那么为什么不再选几位呢?
在JDK8源码中
java.lang.Integer有52429作为常量出现,
为什么有52429的常量呢?
static void getChars(int i, int index, char[] buf) {int q, r;int charPos = index;char sign = 0;if (i < 0) {sign = '-';i = -i;}// Generate two digits per iterationwhile (i >= 65536) {q = i / 100;// really: r = i - (q * 100);r = i - ((q << 6) + (q << 5) + (q << 2));i = q;buf [--charPos] = DigitOnes[r];buf [--charPos] = DigitTens[r];}// Fall thru to fast mode for smaller numbers// assert(i <= 65536, i);for (;;) {q = (i * 52429) >>> (16+3); //相当于i/10;r = i - ((q << 3) + (q << 1)); // r = i-(q*10) ...buf [--charPos] = digits [r];i = q;if (i == 0) break;}if (sign != 0) {buf [--charPos] = sign;}
}public static String toString(int i) {if (i == Integer.MIN_VALUE)return "-2147483648";int size = (i < 0) ? stringSize(-i) + 1 : stringSize(i);char[] buf = new char[size];getChars(i, size, buf);return new String(buf, true);
}
固定的形式是一个整型变量乘上52429,然后向右移19位。很自然想到2^19=524288,那么这个52429就不难理解了,应该就是除10的操作。
除法是很慢的,而乘法和以为却相对较快,所以为了优化这一点点的速度,java采用了乘52429再移19位的方法。
对于为什么选择52429?
这里列出几个取值的精度:
103/1024≈0.1006 (2^10)205/2048≈0.100098 (2^11)……26215/262144≈0.100002 (2^18)52429/524288≈0.10000038 (2^19)104858/1048576≈0.10000038 (2^20)
可见,到2^19次方左右,除10的精度已经非常高了。
那么为什么不再选几位呢?
原因很简单:
- java中整型占32位,而52429的二进制是1100110011001101(16位),65535的二进制是111111111111111(16位),相乘结果为31位。
- 通过阅读上述源码的这个方法可知,i是不会大于65535的(注释中也提到:assert(i <= 65536, i);),所以算上符号位,能达到精度最大而又不溢出的也就是2^19了。
相关文章:

Java源码解读之常量52429
文章目录 为什么有52429的常量呢?对于为什么选择52429?那么为什么不再选几位呢? 在JDK8源码中 java.lang.Integer有52429作为常量出现, 为什么有52429的常量呢? static void getChars(int i, int index, char[] buf) {int q, r;…...

“Photoshop AI插件:StartAI的全面使用攻略
随着人工智能技术的飞速发展,Photoshop作为设计师们不可或缺的工具,也在不断地融入AI技术,以提升设计效率和效果。在2024年,PSAI插件StartAI因其强大的功能和易用性,成为了Photoshop用户的得力帮手。下面来给大家详细介…...
入门Axure:快速掌握原型设计技能
2002 年,维克托和马丁在旧金山湾区的一家初创公司工作,发现自己一再被软件开发生命周期的限制所困扰,而且产品团队在编写规范之前很难评估他们的解决方案,开发人员经常不理解(或不阅读)给出的规范ÿ…...

Java中的序列化与反序列化详解
Java中的序列化与反序列化详解 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 什么是序列化与反序列化? 序列化(Serialization&#…...

在鸿蒙开发中如何实现皮肤切换?
在鸿蒙开发中,实现主题皮肤切换可以通过以下步骤: 1. 创建不同的主题样式文件,例如theme_light.json和theme_dark.json。 2. 在应用程序的config.json文件中,引入这些主题样式文件。 3. 在应用程序的入口文件(例如main…...

FlowUs新一代内容创作营销平台|FlowUs息流国产 好用 不限速
FlowUs 作为一个知识管理和协作平台,知识库功能可以被视为一个强大的学习工具! 为什么FlowUs知识库可以成为学习利器呢?原因有以下几点 集中化知识存储:FlowUs允许我们将所有相关信息和资料集中在一个地方,便于访问和复…...
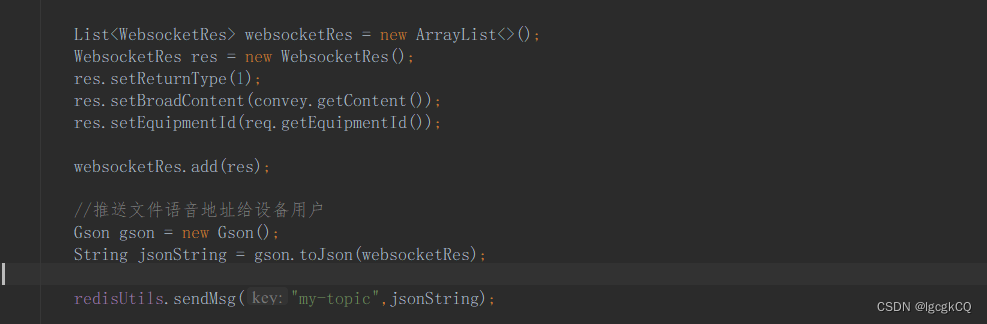
WebSocket解决方案(springboot 基于Redis发布订阅)
WebSocket 因为一般的请求都是HTTP请求(单向通信),HTTP是一个短连接(非持久化),且通信只能由客户端发起,HTTP协议做不到服务器主动向客户端推送消息。WebSocket确能很好的解决这个问题&…...
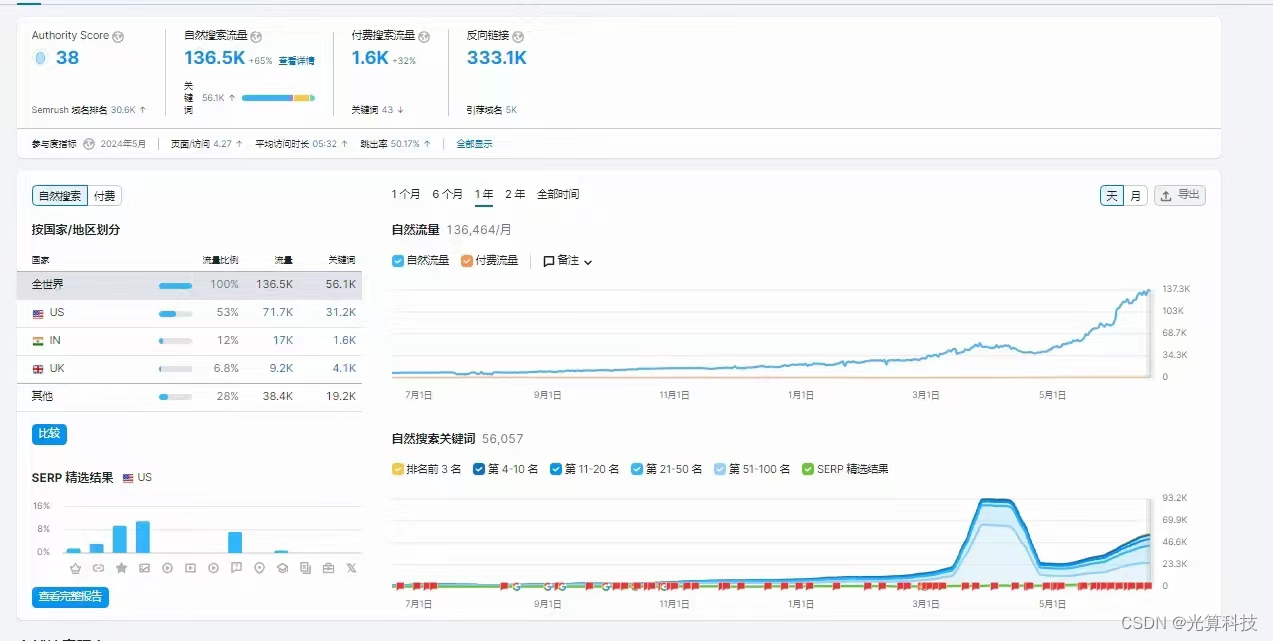
如何优化网站SEO排名?
选择那些容易排名的关键词。使用工具找到那些竞争少但有流量的词语。其次,内部链接非常重要。通过合理的内部链接,可以提升各个页面的权重。 增加FAQ部分能帮助你捕捉更多的长尾关键词流量。争取出现在精选摘要的位置,可以直接提升你的曝光率…...
基于Java的音乐网站系统-计算机毕业设计源码01239
目 录 摘要 1 绪论 1.1 研究背景 1.2系统开发目标、意义 1.3研究内容 2 相关技术介绍 2.1 MySQL数据库 2.2 Java编程语言 2.3 SpringBoot框架介绍 3 系统需求分析与设计 3.1 可行性分析 3.1.1 技术可行性分析 3.1.2 经济可行性分析 3.1.3 法律可行性分析 3.2 需…...

云原生之容器编排实践-OpenEuler23.09在线安装Kubernetes与KubeSphere
背景 前几篇文章中介绍了如何将 ruoyi-cloud 项目部署到 Kubernetes 集群中,包括网关服务、认证服务和系统服务并且对全部服务采用 YAML 文件的方式来进行部署,这虽然有助于理解 K8S 组织管理资源的风格与底层机制,但是对于团队中不太熟悉命…...

Ubuntu 截图shutter,图像编辑 gimp,录屏kazam
1.截图: Shutter 安装shutter命令: sudo add-apt-repository ppa:shutter/ppasudo apt-get updatesudo apt-get install shutter 2.图片编辑:Gimp, Kolourpaint, Pinta gimp全名为:GNU Image Manipulation Program,…...

WSO2 products 文件上传漏洞(CVE-2022-29464)
前言 CVE-2022-29464 是一个影响多个 WSO2 产品的严重远程代码执行(RCE)漏洞。这些产品包括 WSO2 API Manager、WSO2 Identity Server 和 WSO2 Enterprise Integrator 等。由于用户输入验证不当,该漏洞允许未经身份验证的攻击者在服务器上上…...
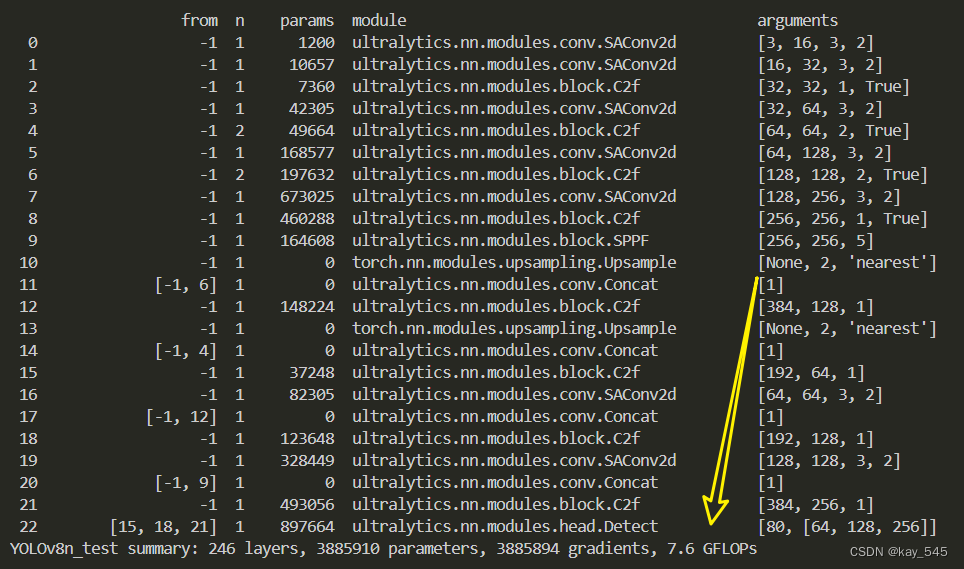
YOLOv8改进 | 卷积模块 | SAConv可切换空洞卷积
秋招面试专栏推荐 :深度学习算法工程师面试问题总结【百面算法工程师】——点击即可跳转 💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 专栏目录 :《YOLOv8改进有效…...

使用Python下载并合并HLS视频片段
下载和合并视频片段的实用方法 在日常工作中,我们经常会遇到需要从网上下载视频并将其合并成一个完整视频的需求。本文将介绍如何使用 Python 下载多个视频片段,并使用 ffmpeg 将这些片段合并成一个完整的视频文件。以下是具体步骤和代码实现。 完整代…...

常见的九种二极管
常见的九种二极管 文章目录 常见的九种二极管1、普通二极管2、光电二极管(LED)3、变容二级管4、发光二极管5、恒流二极管6、快恢复二极管(FRD)7、肖特基二极管8、瞬态电压抑制二极管(TVS)9、齐纳二极管(稳压࿰…...
竞赛选题 python的搜索引擎系统设计与实现
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 python的搜索引擎系统设计与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:5分创新点:3分 该项目较为新颖ÿ…...

大模型技术方向夏令营1期-对话分角色要素提取挑战赛
#AI夏令营 #Datawhale #夏令营 一、 baseline 跑通 Baseline 本身挑战性有限,关键是熟悉 LLM-centric 相关任务 coding 层面的流程方法,比如: 大模型 API(这里为科大讯飞 Spark)调用token消耗的理解如何调用大模型实现针对给定…...
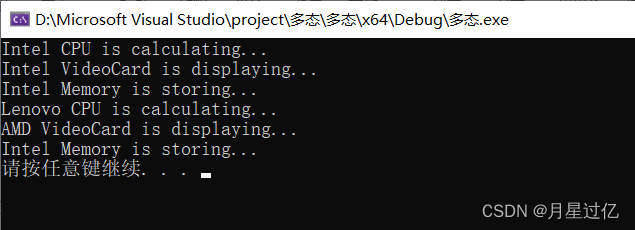
类和对象(封装、继承、多态、友元)
c面相对象的三大特性为:封装、继承、多态 c 认为万事万物都皆为对象,对象上有其属性和行为 一、类和对象(封装) (一)封装的意义 封装是c面相对象的三大特性之一 封装的意义: 将属性和行为…...

关于Yolov8我踩过的那些坑
按照报错频次梳理: 致命反斜杠‘\’ 调用模型时,我喜欢‘copy relative location’,然后win系统默认反斜杠! 就导致路径读取错误!各种报错!! debug到崩溃然后发现是斜杠的问题,本吗喽…...
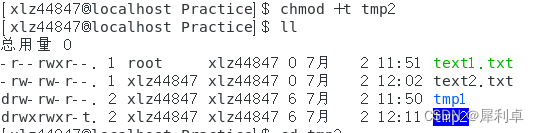
Linux——shell原理和文件权限
1.shell原理 在我们使用云服务器时,需要通过shell进行使用,而shell则是一种外壳程序。 我们提到过,大部分的指令实际上就是文件,当用户需要执行某种功能时,由于用户不擅长和操作系统直接交互(操作复杂&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
