数据在内存中的存储方式
🌟🌟作者主页:ephemerals__
🌟🌟所属专栏:C语言
目录
前言
一、整数的存储
二、大小端字节序及其判断
1.什么是大小端
2.为什么有大小端
3.用c语言编写程序判断大小端
三、浮点数的存储
1.浮点数的存储规则
2.浮点数的存储过程:
3.浮点数的读取过程:
总结
前言
我们都知道,在计算机中,数据都是以二进制的形式存储的。但是对于整数和浮点数而言,它们的存储方式却略有不同。今天我们深入探讨以下整数和浮点数在内存中的存储。
一、整数的存储
整数的二进制表示方法有三种:原码,反码和补码。当表示有符号的整数时,这三种表示方法都有符号位和数值位两部分,符号位占一个二进制位(最高位),数值位占其余二进制位,当符号位为0时,表示这是一个正数,为1时表示这是一个负数。
这里需要注意以下两点:
1.正整数的源码,反码和补码相同。
2.对于负整数,三者均不相同:
原码:直接将数值翻译成二进制数。
反码:符号位不变,数值位按位取反。
补码:源码+1得到补码。
正数的存储方式:一律以补码的形式存储。
二、大小端字节序及其判断
首先,我们来运行一段代码:
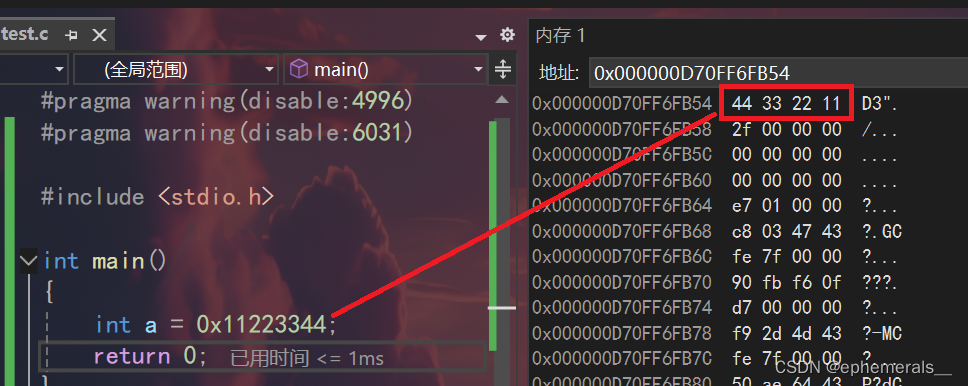
我们给a赋值0x11223344,但是在内存窗口中这四个字节的内容却是倒着排放的。这是为什么呢?
这就涉及到大小端的问题了。
1.什么是大小端
对于一个超过一字节的数据,在内存中存储的时候我们就需要考虑到字节排列的顺序问题。我们根据不同的字节存储顺序,将其分为大端字节序和小端字节序。它们的含义是:
大端字节序表示低位的字节内容存放在高地址处,高位字节内容存放在低地址处。
小端字节序表示低位的字节内容存放在低地址处,高位字节内容存放在高地址处。
我们画图表示以下大小端的含义:
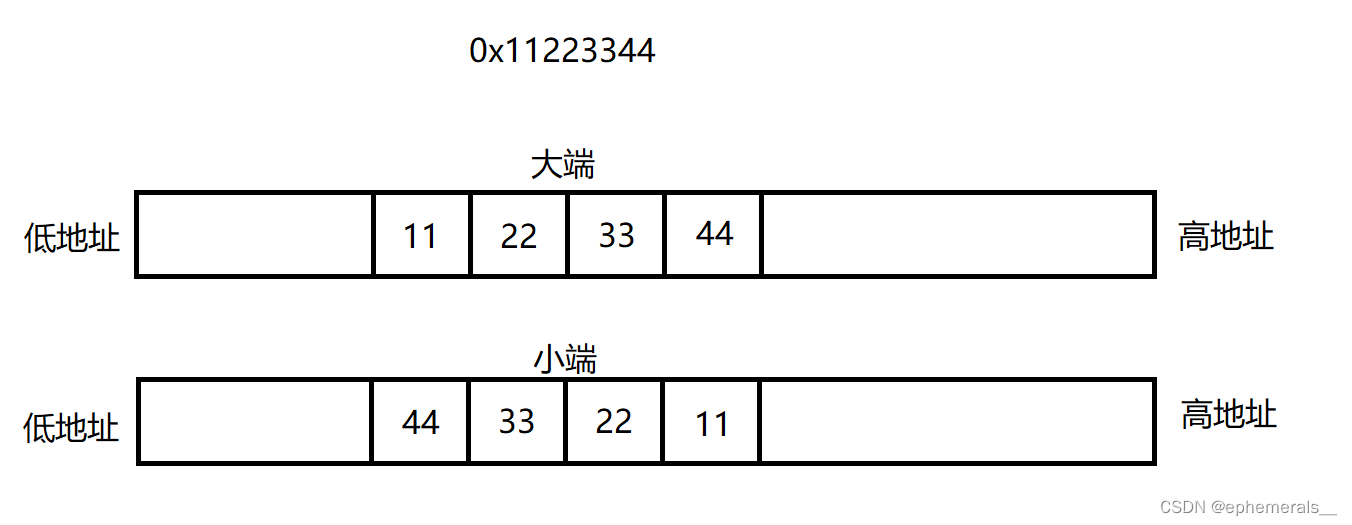
2.为什么有大小端
那么,为什么会有大小端呢?
因为在很多编程语言当中,许多数据类型的内存大小是大于一个字节(8bit)的,它们存储在宽度大于一个字节的寄存器当中时,必然存在多个字节安排顺序的问题。因此,大端字节序和小端字节序就出现了。
3.用c语言编写程序判断大小端
在了解了大小端的概念及成因后,我们就可以由此来写一个程序,判断当前机器是大端还是小端了:
#include <stdio.h>int main()
{int a = 0x11223344;char* p = &a;//用char型指针访问int型变量,访问其最低地址的空间printf("%x\n", *p);return 0;
}运行结果:

可以看到,程序以十六进制形式打印出了这个数的最低位。由于char型指针访问的是int类型的最低地址空间,这就说明最低地址存放的是低位的字节内容,所以作者的电脑是小端字节序。
三、浮点数的存储
了解了整数的存储之后,我们来探讨一下浮点数的存储。首先我们可以猜一猜以下代码的运行结果:
#include <stdio.h>int main()
{int n = 9;float* p = (float*)&n;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);*p = 9.0f;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);return 0;
}结果如下:

看到结果,想必你会大吃一惊吧!为什么同一个数,以不同的类型输出会有这么大的差异?这就关乎浮点数在内存中的存储了。
1.浮点数的存储规则
根据国际IEEE754标准,任意一个二进制的浮点数都可以表示成如下形式:

其中,
表示符号位,S为0时,表示V是一个正数;S为1时,表示V是一个负数。
表示V的有效数字。
。
表示指数位。
举个例子,对于浮点数5.0,它的二进制形式是101.0,写成科学计数法就是。
这样,根据刚才的格式,S=0,M=1.01,E=2。
我们可以发现:对于一个浮点数,只要知道了S,M,E这三个值,就能得出这个浮点数的值。在计算机中,浮点数也是将这三个数存储到内存中,使用时根据规则就能够得到该值。这三个数的存储规则如下:
对于32位的浮点数,最高位存储S,接下来的8位存储E,剩下的23位存储M。
对于64位的浮点数,最高位存储S,接下来的11位存储E,剩下的52位存储M。


2.浮点数的存储过程:
1.对于有效数字M,由于
,就是1.xxxxxx的形式,那么这个个位数“1”就可以不用存储,只存储小数部分,这样就可以多存储一位有效数字。
2.对于指数E,首先这里的E一定是一个无符号整数,但是科学计数法的指数是可以出现负数的,所以,IEEE754规定:存入E时,要给它加上一个中间数再存储。对于8位的E,中间数是127;对于11位的E,这个中间数是1023。
3.浮点数的读取过程:
浮点数的读取过程分三种情况:
1.E的各位不全为0或者不全为1:此时,将E的值取出并减去127(或1023),得到真实值,然后将有效数字M加上1。
2.E全为0:此时,E的真实值变成1-127(或1-1023),并且M不再加1,这用于表示±0或者极小的数字。
3.E全为1:此时,如果有效数字M全为0,这个数就表示正负无穷大(符号由S决定)。
了解了浮点数的存储规则,存储过程和读取过程之后,之前代码的运行结果就能够说明白了。
总结
这篇文章我们探讨了整数的存储、大小端的概念和判断方式、浮点型数据的存储规则,存储过程和读取过程,进一步了解了计算机底层数据的存储模式。之后博主会继续跟大家分享c语言相关内容,感谢大家的支持❤❤❤
相关文章:
数据在内存中的存储方式
🌟🌟作者主页:ephemerals__ 🌟🌟所属专栏:C语言 目录 前言 一、整数的存储 二、大小端字节序及其判断 1.什么是大小端 2.为什么有大小端 3.用c语言编写程序判断大小端 三、浮点数的存储 1.浮点数…...

Selenium 监视数据收发
实际上,在我提供的示例中,确实使用了浏览器实例。webdriver.Chrome()这行代码正是创建了一个Chrome浏览器的WebDriver实例。Selenium Wire扩展了标准的Selenium WebDriver,允许你通过这个浏览器实例来监听网络请求。 当你运行类似这样的代码…...

基于 STM32 的智能睡眠呼吸监测系统设计
本设计的硬件构成: STM32F103C8T6单片机最小系统板(包含3.3V稳压电路时钟晶振电路复位电路(上电自复位,手动复位)),心率传感器、气压传感器、液晶显示、按键、蜂鸣器、LED灯、蓝牙模块组合而成…...

Spring的事务管理、AOP实现底层
目录 spring的事务管理是如何实现的? Spring的AOP的底层实现原理 spring的事务管理是如何实现的? 首先,spring的事务是由aop来实现的,首先要生成具体的代理对象,然后按照aop的整套流程来执行具体的操作逻辑ÿ…...
基于SpringBoot的篮球竞赛预约平台
你好,我是计算机学姐码农小野!如果你对篮球竞赛预约平台感兴趣或有相关需求,欢迎私信联系我。 开发语言: Java 数据库: MySQL 技术: SpringBootMySql 工具: MyEclipse、Tomcat 系统展示…...

学生用小台灯什么牌子的好?列举出几款学生用台灯推荐
眼睛是我们感知世界的窗口,但近年来,儿童青少年的视力健康却受到了严重困扰。数据显示,近视问题在儿童群体中呈现出明显的增长趋势,这给他们的学习和生活带来了诸多不便。虽然现代科技的快速发展使得电子产品成为了我们生活中不可…...

软件测试面试题:项目中的MQ是如何测试的?
通常,咱们会从两个方面来考虑:正常情况和异常情况。 首先,咱们得确保消息队列在正常工作时结果正确。比如,消息发送出去的时候,所有的字段都得齐全,接收方收到的消息也得一样。咱们得确保系统能够正确无误…...
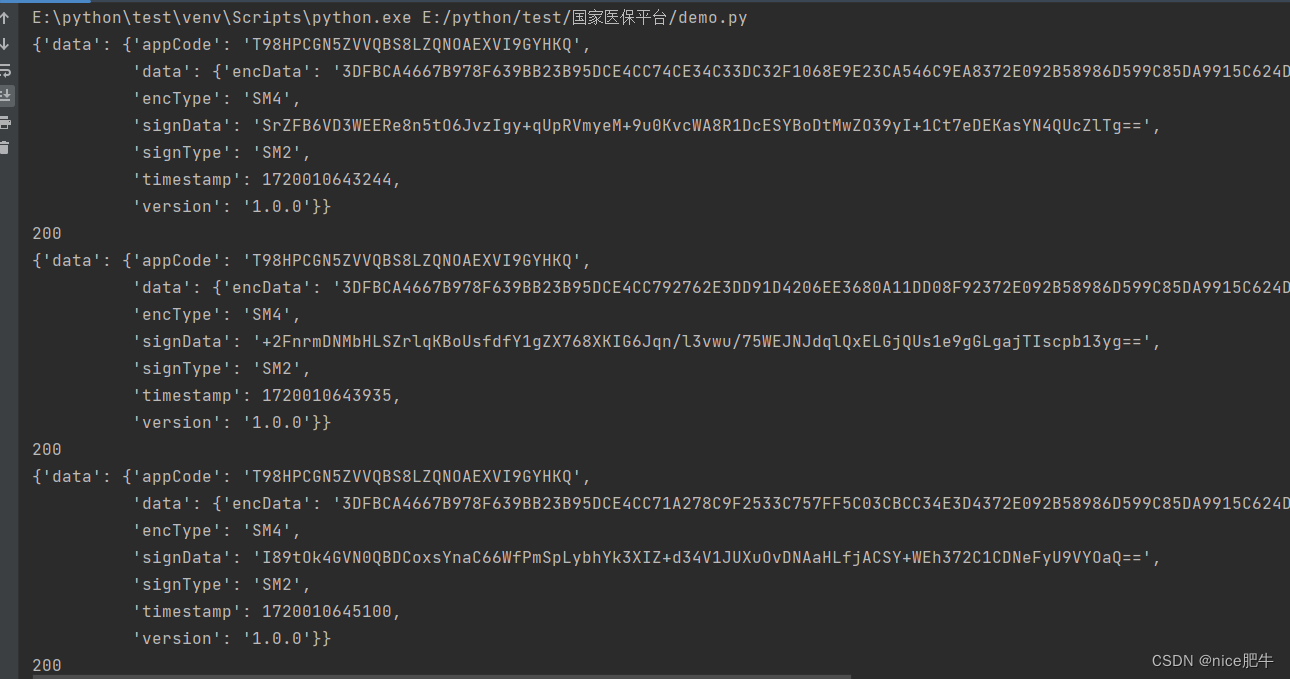
Python爬取国家医保平台公开数据
国家医保服务平台数据爬取python爬虫数据爬取医疗公开数据 定点医疗机构查询定点零售药店查询医保机构查询药品分类与代码查询 等等,数据都能爬 接口地址:/ebus/fuwu/api/nthl/api/CommQuery/queryFixedHospital 签名参数:signData {dat…...
B站大课堂-自动化精品视频(个人存档)
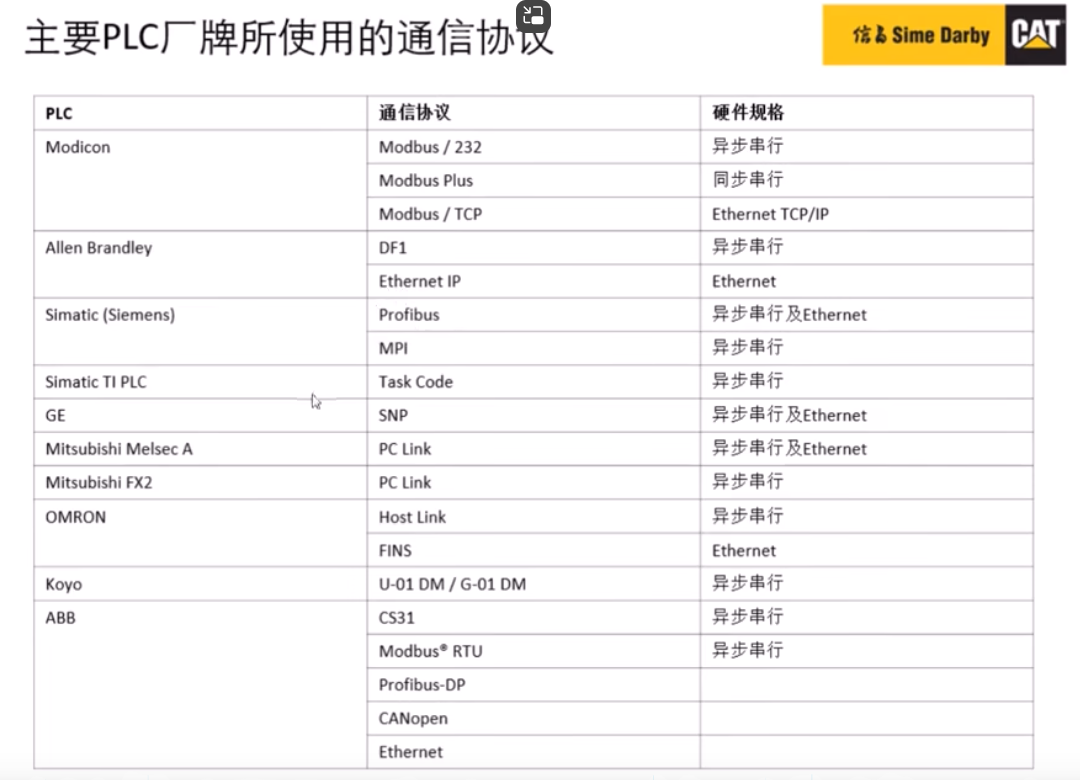
基础知识 工业通信协议 Modbus 施耐德研发,有基于以太网的 ModbusTCP 协议和使用 485/232 串口通信的 ModbusRTU/ASCII。 Modbus 协议面世较早、协议简洁高效、商用免费、功能灵活、实现简单,是目前应用最广泛的现场总线协议。 我的笔记里边有一些推荐…...

C++_STL---priority_queue
priority_queue的相关介绍 优先级队列是一种容器适配器,根据严格的排序标准,它的第一个元素总是它所包含的元素中最大(小)的。该容器适配器类似于堆,在堆中可以随时插入元素,并且可以检索最大(小)堆元素(优先级队列中位于顶部的元…...

可移动天线辅助宽带通信的性能分析和优化
可移动天线辅助宽带通信的性能分析和优化 可移动天线 (MA) 已成为一种很有前景的技术,通过在发射器 (Tx) 和/或接收器 (Rx) 处实现天线的本地移动来实现更有利的信道条件,从而增强无线通信性能。 由于现有的MA辅助无线通信研究主要考虑平坦衰落信道中的…...

h5兼容table ,如何实现h5在app内使用h5渲染table表格而且实现横屏预览?
压图地址 横屏div 通过css 实现 transform: rotate(90deg); transformOrigin: 50vw 50vw ; height: 100vw; width: 100vh;<divclass"popup-box":style"{transform: originSet 0 ? rotate(90deg) : ,transformOrigin: originSet 0 ? 50vw 50vw : ,height…...

在windows上安装objection
安装命令pip install objection -i https://mirrors.aliyun.com/pypi/simple hook指定进程 objection -g 测试 explore 进程名不定是包名,也可能是app名字,如“测试”就是app的名字 若出现如下错误,说明python 缺少setuptools 直接安装setu…...

人脸特征68点识别 C++
1、加载一张图片 main函数: cv::Mat img cv::imread("5.jpg");vector<Point2f> points_vec dectectFace68(img);2、人脸68特征识别函数 在这里vector<Point2f> dectectFace68(Mat src) {vector<Point2f> points_vec;int* pResults …...

部署LVS-DR 群集
1 LVS-DR 集群 LVS-DR (Linux Virtual Server Director Server ) 工作模式, 是生产环境中最常用的一种工作模式 1.1:LVS-DR工作原理 LVS-DR 模式, Director Server 作为群集的访问入口, 不作为网关使用,…...
nginx的正向代理和反向代理
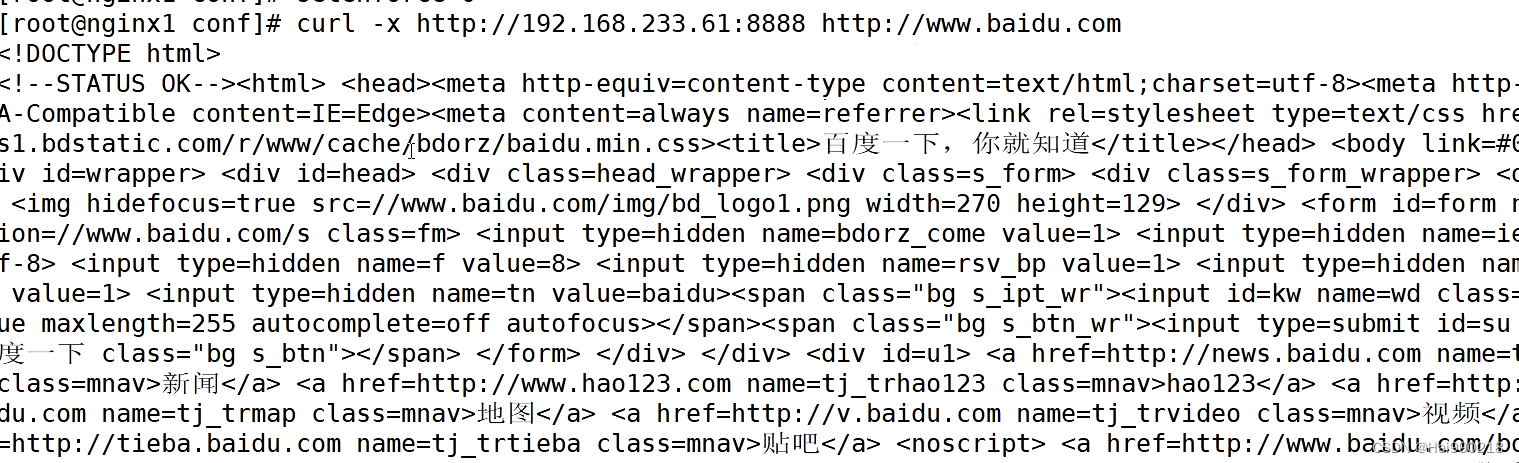
概念 正向代理以及缓存配置 代理:客户端不再是直接访问服务端,通过代理服务器访问服务端。 正向代理:面向客户端,我们通过代理服务器的ip地址访问目标服务器。 服务端只知道代理服务器的地址,真正的客户端ip可以隐…...
米国政府呼吁抛弃 C 和 C++
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 很多观点认为C 或 C永远不可被…...
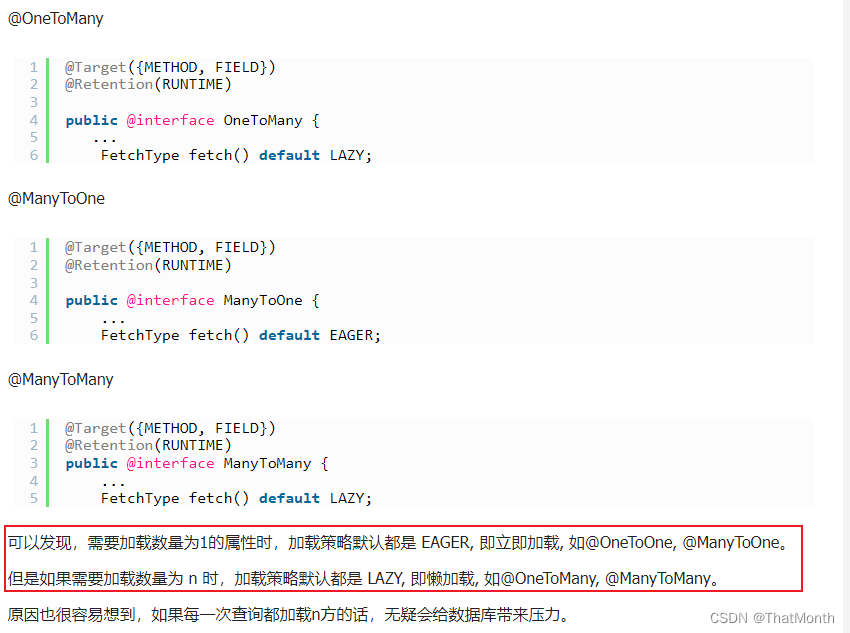
failed to lazily initialize a collection of role,解决Hibernate查询报错
Hibernate报错: org.hibernate.LazyInitializationException: failed to lazily initialize a collection of role: com.jiuqi.gov.common.attatchment.entity.AttachmentEntity.properties, could not initialize proxy - no Session at org.hibernate.co…...
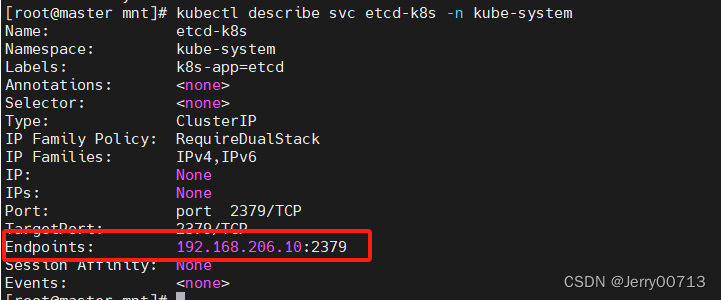
Promethuse-监控 Etcd
一、思路 Prometheus监控Etcd集群,是没有对应的exporter,而 由CoreOS公司开发的Operator,用来扩展 Kubernetes API,特定的应用程序控制器,它用来创建、配置和管理复杂的有状态应用,如数据库、缓存和监控系…...

linux桌面运维---第四天
1、hostnamectl命令: 作用:永久设置主机名 语法:hostnamectl [actions][name strings] 动作: status 显示当前主机名设置【掌握】 set-hostname NAME 设置系统主机名【掌握】 set-icon-name NAME 为主…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
