华为OD机考题(HJ50 四则运算)
前言
经过前期的数据结构和算法学习,开始以OD机考题作为练习题,继续加强下熟练程度。
描述
输入一个表达式(用字符串表示),求这个表达式的值。
保证字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’, ‘)’,‘[’, ‘]’,‘{’ ,‘}’。且表达式一定合法。
数据范围:表达式计算结果和过程中满足 ∣𝑣𝑎𝑙∣≤1000 ∣val∣≤1000 ,字符串长度满足 1≤𝑛≤1000 1≤n≤1000
输入描述:
输入一个算术表达式
输出描述:
得到计算结果
示例1
输入:
3+2*{1+2*[-4/(8-6)+7]}
输出:25
实现原理
在 Java 中实现支持负数、大括号、中括号和小括号的四则运算,可以通过以下步骤:
- 处理括号:将中缀表达式中的大括号
{}, 中括号[]和小括号()全部转换成统一的小括号()。 - 中缀转后缀:将中缀表达式转换为后缀表达式(RPN)。
- 计算后缀表达式:使用栈计算后缀表达式的值。
实现代码
import java.util.*;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);String expression = in.nextLine();expression = replaceBrackets(expression);List<String> postfix = infixToPostfix(expression);int result = evaluatePostfix(postfix);System.out.println(result);}// 判断是否是运算符private static boolean isOperator(char c) {return c == '+' || c == '-' || c == '*' || c == '/';}// 获取运算符的优先级private static int precedence(char c) {switch (c) {case '+':case '-':return 1;case '*':case '/':return 2;default:return -1;}}// 将表达式中的大括号和中括号替换为小括号private static String replaceBrackets(String expression) {return expression.replace('{', '(').replace('}', ')').replace('[', '(').replace(']', ')');}// 将中缀表达式转换为后缀表达式public static List<String> infixToPostfix(String expression) {Stack<Character> stack = new Stack<>();List<String> postfix = new ArrayList<>();int n = expression.length();for (int i = 0; i < n; i++) {char c = expression.charAt(i);// 如果是数字或者负号开头的数字if (Character.isDigit(c) || (c == '-' && (i == 0 ||expression.charAt(i - 1) == '('))) {StringBuilder number = new StringBuilder();number.append(c);i++;while (i < n && Character.isDigit(expression.charAt(i))) {number.append(expression.charAt(i));i++;}i--;postfix.add(number.toString());}// 左括号else if (c == '(') {stack.push(c);}// 右括号else if (c == ')') {while (!stack.isEmpty() && stack.peek() != '(') {postfix.add(String.valueOf(stack.pop()));}stack.pop();}// 运算符else if (isOperator(c)) {while (!stack.isEmpty() && precedence(stack.peek()) >= precedence(c)) {postfix.add(String.valueOf(stack.pop()));}stack.push(c);}}// 将栈中剩余的运算符添加到后缀表达式while (!stack.isEmpty()) {postfix.add(String.valueOf(stack.pop()));}return postfix;}// 计算逆波兰表达式的值public static int evaluatePostfix(List<String> postfix) {Stack<Integer> stack = new Stack<>();for (String token : postfix) {if (isOperator(token.charAt(0)) && token.length() == 1) {int b = stack.pop();int a = stack.pop();switch (token.charAt(0)) {case '+':stack.push(a + b);break;case '-':stack.push(a - b);break;case '*':stack.push(a * b);break;case '/':if (b == 0) {throw new ArithmeticException("除数不能为零");}stack.push(a / b);break;}} else {stack.push(Integer.parseInt(token));}}return stack.pop();}
}函数说明:
-
isOperator 方法:
- 判断一个字符是否是运算符(+、-、*、/)。
-
precedence 方法:
- 获取运算符的优先级,* 和 / 的优先级高于 + 和 -。
-
replaceBrackets 方法:
- 将表达式中的大括号
{}和中括号[]替换为小括号()。
- 将表达式中的大括号
-
infixToPostfix 方法:
- 将中缀表达式转换为后缀表达式。使用栈处理运算符和括号,处理过程中需要特别注意负数的情况。
-
evaluatePostfix 方法:
- 使用栈计算后缀表达式的值。遍历后缀表达式的每个 token,如果是运算符,则从栈中弹出两个操作数进行计算,并将结果压入栈中;如果是数字,则直接压入栈中。
1.QA:
相关文章:
)
华为OD机考题(HJ50 四则运算)
前言 经过前期的数据结构和算法学习,开始以OD机考题作为练习题,继续加强下熟练程度。 描述 输入一个表达式(用字符串表示),求这个表达式的值。 保证字符串中的有效字符包括[‘0’-‘9’],‘’,‘-’, ‘*’,‘/’ …...

SpringBoot实现文章点赞功能
提示:今日是2024年的6月30日,未来的你看到这篇文章,希望你依旧快乐 文章目录 前言 首先在这里前缀部分我就不做要求了,比如说登录信息什么的 数据库表格 这里实现点赞功能,主要是围绕论坛项目完成的 user_info代表用户信息表 for…...

产品经理系列1—如何实现一个电商系统
具体笔记如下,主要按获客—找货—下单—售后四个部分进行模块拆解...
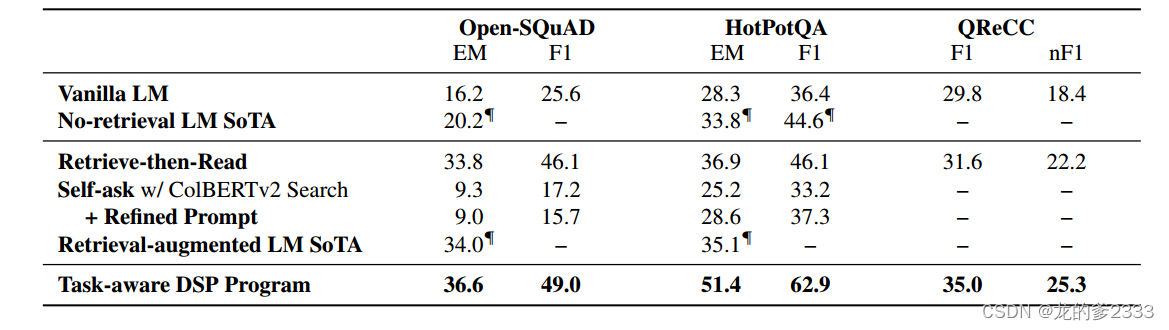
论文翻译 | (DSP)展示-搜索-预测:为知识密集型自然语言处理组合检索和语言模型
摘要 检索增强式上下文学习已经成为一种强大的方法,利用冻结语言模型 (LM) 和检索模型 (RM) 来解决知识密集型任务。现有工作将这些模型结合在简单的“检索-读取”流程中,其中 RM 检索到的段落被插入到 LM 提示中。 为了充分发挥冻结 LM 和 RM 的…...

1.(vue3.x+vite)实现卷帘效果
前端技术社区总目录(订阅之前请先查看该博客) 1:效果预览 2:代码编写 <template><div style="width...
HMI 的 UI 风格成就经典
HMI 的 UI 风格成就经典...

金融(基金)行业信创国产化特点及统一身份认证解决方案
金融业在政策支持及自主驱动下,金融信创取得快速发展。从2020年开始,三期试点已扩容至5000余家,进入全面推广阶段。而基金行业信创建设与银行、证券、保险这些试点行业相比,进展较为缓慢。 基金行业信创当前面临的问题 与多家基…...

透过 Go 语言探索 Linux 网络通信的本质
大家好,我是码农先森。 前言 各种编程语言百花齐放、百家争鸣,但是 “万变不离其中”。对于网络通信而言,每一种编程语言的实现方式都不一样;但其实,调用的底层逻辑都是一样的。linux 系统底层向上提供了统一的 Sock…...

【C语言】—— 文件操作(下)
【C语言】—— 文件操作(下) 前言:五、文件的顺序读写5.1、 顺序读写函数介绍5.2、 f p u t c fputc fputc 函数5.3、 f g e t c fgetc fgetc 函数5.4、 f p u t s fputs fputs 函数5.5、 f g e t s fgets fgets 函数5.6、 f p r i n t f…...

np.argsort
函数解释 np.argsort是NumPy库中的一个函数,用于对数组进行排序并返回排序后的索引。它不会直接对数组进行排序,而是返回一个数组,这个数组中的元素是原数组中元素按升序排序后的索引。 numpy.argsort(a, axis-1, kindNone, orderNone) 参…...

ORC与Parquet列式存储的区别
ORC与Parquet列式存储 1、ORC与Parquet列式存储2、ORC与Parquet的区别 列式存储(Columnar Storage)是一种优化的数据存储方式,与传统的行式存储(Row Storage)相比,列式存储在数据压缩、查询性能、I/O效率等…...
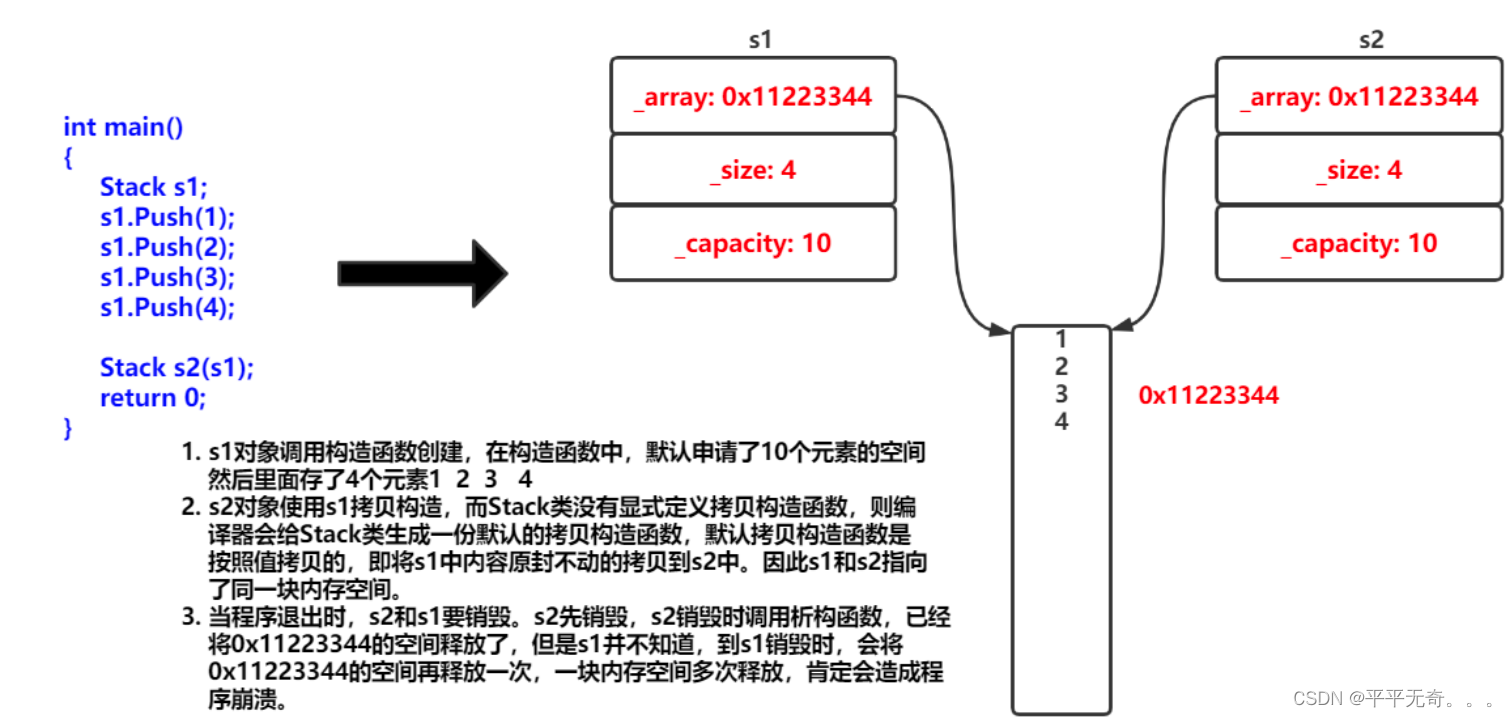
析构函数和拷贝构造函数
文章目录 析构函数1.析构函数的定义:2.析构函数的语法:3.析构函数的特性: 拷贝构造函数1.拷贝构造函数的定义:2.拷贝构造函数的语法3.拷贝构造函数的特性(1)拷贝构造函数是构造函数的一个重载形式**(这个其实也很好理解࿰…...

sql server启动、连接 与 navicat连接sql server
一、sql server 启动 1.搜索cmd->以管理员身份运行 2.输入以下命令 net start mssqlserver 3.服务器启动成功 二、sql server连接 1.打开ssms,输入,连接 2.右键,属性 3.连接,勾选允许远程连接到此服务器 三、navicat连接sq…...

数据库测试数据准备厂商 Snaplet 宣布停止运营
上周刚获知「数据库调优厂商 OtterTune 宣布停止运营」。而今天下班前,同事又突然刷到另一家海外数据库工具商 Snaplet 也停止运营了。Snaplet 主要帮助开发团队在数据库中生成仿真度高且合规的测试数据。我们在年初还撰文介绍过它「告别手搓!Postgres 一…...
)
【Java09】方法(下)
1. 形参个数可变的方法 Java允许方法指定数量不确定的形参。如果在定义方法是,在最后一个形参的类型后加...,则表明该形参可以接受多个参数值。多个参数值作为数组传入: public class Varargs {public static void test(int a, String... b…...

d88888888
分析:v9999999999 vn输出n个n 先算出n的位数p 所以答案是nn*10的p次方n*10的2p次方.....n*10的(n-1)p次方 化简n*(10的0次方10的p次方10的2p次方.....10的(n-1)p次方) 后面为等比数列求和 …...

【MySQL备份】mysqldump基础篇
目录 1.简介 2.基本用途 3.命令格式 3.1常用选项 3.2常用命令 4.备份脚本 5.定时执行备份脚本 1.简介 mysqldump 是 MySQL 数据库管理系统的命令行实用程序,用于创建数据库的逻辑备份。它能够导出数据库的结构(如表结构、视图、触发器等…...

C# Halcon目标检测算法
在Halcon中进行目标检测可以使用传统的计算机视觉方法,也可以使用深度学习的方法。Halcon提供了丰富的函数库来处理这些任务,而在C#中使用Halcon,你需要通过Halcon .NET接口。 以下是使用Halcon进行目标检测的一般步骤,这里我将给…...

7.4总结
今天写了几道题目 最近,一年级学生马克西姆学习了科拉兹猜想,但他在讲课时没有太注意,所以他认为猜想中提到了以下过程: 有一个变量 $$$x$$$ 和一个常数 $$$y$$$ 。下面的操作要执行 $$$k$$$ 次: - 将 $$$x$$$ 增加…...

知识图谱查询语言的表示
文章目录 SPARQL知识图谱查询基本构成常见的SPARQL查询算子语义Markup表示语言SPARQL知识图谱查询基本构成 RDF 支持类似数据库的查询语言,叫作SPARQL,它提供了查询RDF 数据的标准语法、处理SPARQL查询的规则以及结果返回形式。 变量,RDF中的资源,以“?”或者“$”指示;…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
