【高阶数据结构】图的应用--最短路径算法
文章目录
- 一、最短路径
- 二、单源最短路径--Dijkstra算法
- 三、单源最短路径--Bellman-Ford算法
- 四、多源最短路径--Floyd-Warshall算法
一、最短路径
最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
二、单源最短路径–Dijkstra算法
单源最短路径问题:给定一个图G = ( V , E ) G=(V,E)G=(V,E),求源结点s ∈ V s∈Vs∈V到图中每个结点v ∈ V v∈Vv∈V的最短路径。Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题,同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点,所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。
针对一个带权有向图G,将所有结点分为两组S和Q,S是已经确定最短路径的结点集合,在初始时为空(初始时就可以将源节点s放入,毕竟源节点到自己的代价是0),Q 为其余未确定最短路径的结点集合,每次从Q 中找出一个起点到该结点代价最小的结点u ,将u 从Q 中移出,并放入S 中,对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ,判断源节点s到结点u 的代价与u 到v 的代价之和是否比原来s 到v 的代价更小,若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和,否则维持原样。如此一直循环直至集合Q 为空,即所有节点都已经查找过一遍并确定了最短路径,至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值,不发生变化。Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新,并加入S中,所以该算法使用的是贪心策略。
Dijkstra算法存在的问题是不支持图中带负权路径,如果带有负权路径,则可能会找不到一些路径的最短路径。

代码实现:
// 临接矩阵
namespace Matrix
{template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, MAX_W, Direction> Self;private:std::vector<V> _vertexs; // 顶点集合std::map<V, size_t> _vIndexMap; // 顶点的下标映射关系std::vector<std::vector<W>> _matrix; // 存储边集合的矩阵void PrintShortPath(const V &src, const std::vector<W> &dist, const std::vector<int> &pPath){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; ++i){if (i != srci){// 找出i顶点的路径std::vector<int> path;size_t parenti = i;while (parenti != srci){path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);reverse(path.begin(), path.end());for (auto index : path){std::cout << _vertexs[index] << "->";}std::cout << "权值和:" << dist[i] << std::endl;}}}// 顶点个数是N -> 时间复杂度:O(N^2)空间复杂度:O(N)void Dijkstra(const V &src, std::vector<W> &dist, std::vector<int> &pPath){size_t srci = GetVertexIndex(src);int n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = 0;pPath[srci] = srci;// 已经确定最短路径的顶点集合std::vector<bool> S(n, false);// n个节点每个节点都要作为起点for (int i = 0; i < n; i++){// 选最短路径顶点且不在S更新其他路径int u = 0;W min = MAX_W;for (int j = 0; j < n; j++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}S[u] = true;// 松弛更新u连接顶点v srci->u + u->v < srci->v 更新for (int v = 0; v < n; v++){if (S[v] == false && _matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}}}}};
}
测试代码:
void TestGraphDijkstra()
{const char *str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);std::vector<int> dist;std::vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrintShortPath('s', dist, parentPath);// // 图中带有负权路径时,贪心策略则失效了。// // 测试结果可以看到s->t->y之间的最短路径没更新出来// const char *str = "sytx";// Graph<char, int, INT_MAX, true> g(str, strlen(str));// g.AddEdge('s', 't', 10);// g.AddEdge('s', 'y', 5);// g.AddEdge('t', 'y', -7);// g.AddEdge('y', 'x', 3);// std::vector<int> dist;// std::vector<int> parentPath;// g.Dijkstra('s', dist, parentPath);// g.PrintShortPath('s', dist, parentPath);
}
三、单源最短路径–Bellman-Ford算法
Dijkstra算法只能用来解决正权图的单源最短路径问题,但有些题目会出现负权图。这时这个算法就不能帮助我们解决问题了,而bellman—ford算法可以解决负权图的单源最短路径问题。它的优点是可以解决有负权边的单源最短路径问题,而且可以用来判断是否有负权回路。它也有明显的缺点,它的时间复杂度 O(NE) (N是点数,E是边数)普遍是要高于Dijkstra算法O(N²)的。像这里如果我们使用邻接矩阵实现,那么遍历所有边的数量的时间复杂度就是O(N^3),这里也可以看出来Bellman-Ford就是一种暴力求解更新。

代码实现:
// 临接矩阵
namespace Matrix
{template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, MAX_W, Direction> Self;private:std::vector<V> _vertexs; // 顶点集合std::map<V, size_t> _vIndexMap; // 顶点的下标映射关系std::vector<std::vector<W>> _matrix; // 存储边集合的矩阵void PrintShortPath(const V &src, const std::vector<W> &dist, const std::vector<int> &pPath){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; ++i){if (i != srci){// 找出i顶点的路径std::vector<int> path;size_t parenti = i;while (parenti != srci){path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);reverse(path.begin(), path.end());for (auto index : path){std::cout << _vertexs[index] << "->";}std::cout << "权值和:" << dist[i] << std::endl;}}}// 时间复杂度:O(N^3) 空间复杂度:O(N)bool BellmanFord(const V &src, std::vector<W> &dist, std::vector<int> &pPath){size_t n = _vertexs.size();size_t srci = GetVertexIndex(src);// vector<W> dist,记录srci-其他顶点最短路径权值数组dist.resize(n, MAX_W);// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组pPath.resize(n, -1);// 先更新srci->srci为缺省值dist[srci] = W();// 总体最多更新n轮for (int k = 0; k < n; k++){bool update = false;std::cout << "更新第:" << k << "轮" << std::endl;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){// srci -> i i -> jif (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){update = true;std::cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << std::endl;dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;}}}// 如果这个轮次中没有更新出更短路径,那么后续轮次就不需要再走了if (update == false)break;}// 还能更新就是带负权回路for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){return false;}}}return true;}};
}
测试代码:
void TestGraphBellmanFord()
{// const char *str = "syztx";// Graph<char, int, INT_MAX, true> g(str, strlen(str));// g.AddEdge('s', 't', 6);// g.AddEdge('s', 'y', 7);// g.AddEdge('y', 'z', 9);// g.AddEdge('y', 'x', -3);// g.AddEdge('z', 's', 2);// g.AddEdge('z', 'x', 7);// g.AddEdge('t', 'x', 5);// g.AddEdge('t', 'y', 8);// g.AddEdge('t', 'z', -4);// g.AddEdge('x', 't', -2);// std::vector<int> dist;// std::vector<int> parentPath;// g.BellmanFord('s', dist, parentPath);// g.PrintShortPath('s', dist, parentPath);// 微调图结构,带有负权回路的测试const char *str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'x', -3);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('y', 's', 1); // 新增g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', -8); // 更改g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);std::vector<int> dist;std::vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath))g.PrintShortPath('s', dist, parentPath);elsestd::cout << "带负权回路" << std::endl;
}
四、多源最短路径–Floyd-Warshall算法
Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。
Floyd算法考虑的是一条最短路径的中间节点,即简单路径p={v1,v2,…,vn}上除v1和vn的任意节点。
设k是p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。p1是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1,2,…,k-1}取得的一条最短路径。


即Floyd算法本质是三维动态规划,D[i][j][k]表示从点i到点j只经过0到k个点最短路径,然后建立起转移方程,然后通过空间优化,优化掉最后一维度,变成一个最短路径的迭代算法,最后即得到所以点的最短路。

代码实现:
// 临接矩阵
namespace Matrix
{template <class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<V, W, MAX_W, Direction> Self;private:std::vector<V> _vertexs; // 顶点集合std::map<V, size_t> _vIndexMap; // 顶点的下标映射关系std::vector<std::vector<W>> _matrix; // 存储边集合的矩阵void PrintShortPath(const V &src, const std::vector<W> &dist, const std::vector<int> &pPath){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; ++i){if (i != srci){// 找出i顶点的路径std::vector<int> path;size_t parenti = i;while (parenti != srci){path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);reverse(path.begin(), path.end());for (auto index : path){std::cout << _vertexs[index] << "->";}std::cout << "权值和:" << dist[i] << std::endl;}}}void FloydWarshall(std::vector<std::vector<W>> &vvDist, std::vector<std::vector<int>> &vvpPath){size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);// 初始化权值和路径矩阵for (int i = 0; i < n; i++){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}// abcdef a {} f || b {} c// 最短路径的更新i-> {其他顶点} ->jfor (int k = 0; k < n; k++){for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){// i -> j i -> k + k -> j// k 作为的中间点尝试去更新i->j的路径if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 找跟j相连的上一个邻接顶点// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是xvvpPath[i][j] = vvpPath[k][j];}}}}// 打印权值和路径矩阵观察数据for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (vvDist[i][j] == MAX_W){printf("%3c", '*');}else{printf("%3d", vvDist[i][j]);}}std::cout << std::endl;}std::cout << std::endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){printf("%3d", vvpPath[i][j]);}std::cout << std::endl;}std::cout << "=================================" << std::endl;}};
}
测试代码:
void TestFloydWarShall()
{const char *str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);std::vector<std::vector<int>> vvDist;std::vector<std::vector<int>> vvParentPath;g.FloydWarshall(vvDist, vvParentPath);// 打印任意两点之间的最短路径for (size_t i = 0; i < strlen(str); ++i){g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);}
}
相关文章:

【高阶数据结构】图的应用--最短路径算法
文章目录 一、最短路径二、单源最短路径--Dijkstra算法三、单源最短路径--Bellman-Ford算法四、多源最短路径--Floyd-Warshall算法 一、最短路径 最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿…...

腾讯云函数node.js返回自动带反斜杠
云函数返回自动带反斜杠 这里建立了如下一个云函数,目的是当APP过来请求的时候响应支持的版本号: use strict; function main_ret(status,code){let ret {status: status,error: code};return JSON.stringify(ret); } exports.main_handler async (event, context) > {/…...

大模型知识学习
大模型训练过程 数据清洗 拟人化描述:知识库整理 预训练 拟人化描述:知识学习可以使用基于BERT预训练模型进行训练 指令微调 拟人化描述:实际工作技能学习实际操作:让大模型模仿具体的输入输出进行拟合,即模仿学…...

JAVA声明数组
一、声明并初始化数组 直接初始化:在声明数组的同时为其分配空间并初始化元素。 int[] numbers {1, 2, 3, 4, 5}; 动态初始化:先声明数组,再为每个元素分配初始值。 double[] decimals;decimals new double[5]; // 分配空间,但…...

VBA通过Range对象实现Excel的数据写入
前言 本节会介绍通过VBA中的Range对象,来实现Excel表格中的单元格写入、区域范围写入,当然也可以写入不同类型的数据,如数值、文本、公式,以及实现公式下拉自动填充的功能。 一、单元格输入数据 1.通过Value方法实现输入不同类型…...

记录OSPF配置,建立邻居失败的过程
1.配置完ospf后,在路由表中不出现ospf相关信息 [SW2]ospf [SW2-ospf-1]are [SW2-ospf-1]area 0 [SW2-ospf-1-area-0.0.0.0]net [SW2-ospf-1-area-0.0.0.0]network 0.0.0.0 Jul 4 2024 22:11:58-08:00 SW2 DS/4/DATASYNC_CFGCHANGE:OID 1.3.6.1.4.1.2011.5.25 .1…...
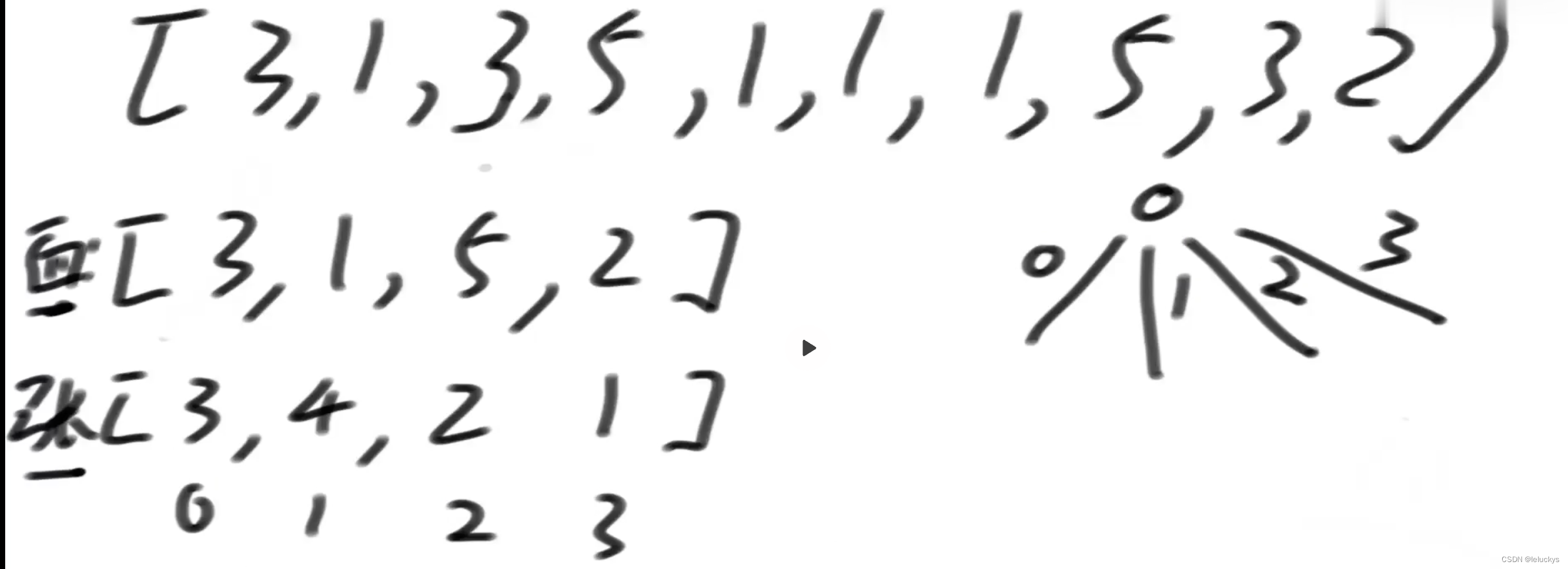
算法体系-25 第二十五节:窗口内最大值或最小值的更新结构
一 滑动窗口设计知识点 滑动窗口是什么? 滑动窗口是一种想象出来的数据结构: 滑动窗口有左边界L和有边界R 在数组或者字符串或者一个序列上,记为S,窗口就是S[L..R]这一部分 L往右滑意味着一个样本出了窗口,R往右滑意味…...

等保2.0中还有哪些针对云计算的安全要求?
等保2.0中针对云计算的安全要求概述 等保2.0是中国信息安全等级保护制度的升级版,它对云计算环境提出了一系列特定的安全要求,以确保云服务的安全性和合规性。以下是一些关键的云计算安全扩展要求: 基础设施位置:要求云计算基础…...

数组与 ArrayList 的区别是什么?
在Java中,数组和ArrayList都是非常常见的数据结构,但它们在使用场景、特点和功能上各有千秋。 理解它们的不同,对于初级Java工程师来说,是提升编程技能的一个重要环节。 下面,我将以一种简单明了的方式,对…...
)
华为OD机考题(HJ50 四则运算)
前言 经过前期的数据结构和算法学习,开始以OD机考题作为练习题,继续加强下熟练程度。 描述 输入一个表达式(用字符串表示),求这个表达式的值。 保证字符串中的有效字符包括[‘0’-‘9’],‘’,‘-’, ‘*’,‘/’ …...

SpringBoot实现文章点赞功能
提示:今日是2024年的6月30日,未来的你看到这篇文章,希望你依旧快乐 文章目录 前言 首先在这里前缀部分我就不做要求了,比如说登录信息什么的 数据库表格 这里实现点赞功能,主要是围绕论坛项目完成的 user_info代表用户信息表 for…...

产品经理系列1—如何实现一个电商系统
具体笔记如下,主要按获客—找货—下单—售后四个部分进行模块拆解...
论文翻译 | (DSP)展示-搜索-预测:为知识密集型自然语言处理组合检索和语言模型
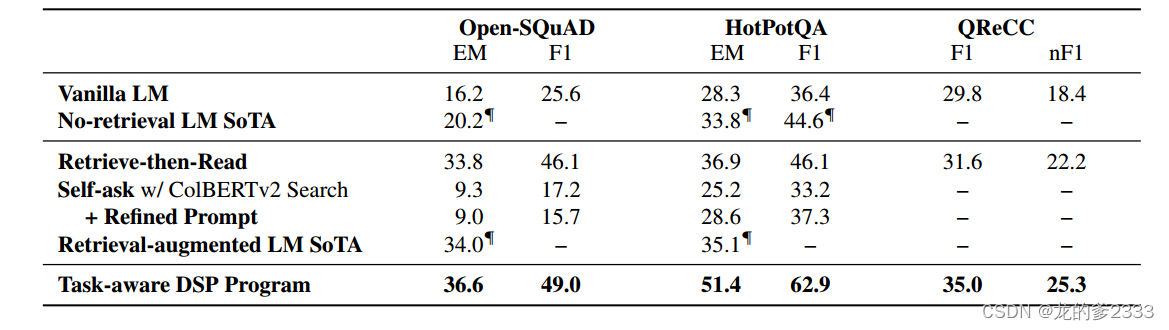
摘要 检索增强式上下文学习已经成为一种强大的方法,利用冻结语言模型 (LM) 和检索模型 (RM) 来解决知识密集型任务。现有工作将这些模型结合在简单的“检索-读取”流程中,其中 RM 检索到的段落被插入到 LM 提示中。 为了充分发挥冻结 LM 和 RM 的…...

1.(vue3.x+vite)实现卷帘效果
前端技术社区总目录(订阅之前请先查看该博客) 1:效果预览 2:代码编写 <template><div style="width...
HMI 的 UI 风格成就经典
HMI 的 UI 风格成就经典...

金融(基金)行业信创国产化特点及统一身份认证解决方案
金融业在政策支持及自主驱动下,金融信创取得快速发展。从2020年开始,三期试点已扩容至5000余家,进入全面推广阶段。而基金行业信创建设与银行、证券、保险这些试点行业相比,进展较为缓慢。 基金行业信创当前面临的问题 与多家基…...

透过 Go 语言探索 Linux 网络通信的本质
大家好,我是码农先森。 前言 各种编程语言百花齐放、百家争鸣,但是 “万变不离其中”。对于网络通信而言,每一种编程语言的实现方式都不一样;但其实,调用的底层逻辑都是一样的。linux 系统底层向上提供了统一的 Sock…...

【C语言】—— 文件操作(下)
【C语言】—— 文件操作(下) 前言:五、文件的顺序读写5.1、 顺序读写函数介绍5.2、 f p u t c fputc fputc 函数5.3、 f g e t c fgetc fgetc 函数5.4、 f p u t s fputs fputs 函数5.5、 f g e t s fgets fgets 函数5.6、 f p r i n t f…...

np.argsort
函数解释 np.argsort是NumPy库中的一个函数,用于对数组进行排序并返回排序后的索引。它不会直接对数组进行排序,而是返回一个数组,这个数组中的元素是原数组中元素按升序排序后的索引。 numpy.argsort(a, axis-1, kindNone, orderNone) 参…...

ORC与Parquet列式存储的区别
ORC与Parquet列式存储 1、ORC与Parquet列式存储2、ORC与Parquet的区别 列式存储(Columnar Storage)是一种优化的数据存储方式,与传统的行式存储(Row Storage)相比,列式存储在数据压缩、查询性能、I/O效率等…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
