代码随想录算法训练营第2天|LeetCode977,209,59
977.有序数组平方
题目链接: 977. 有序数组的平方 - 力扣(LeetCode)文章讲解:代码随想录
视频讲解: 双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
第一想法
暴力算法肯定是先将元素平方,然后Arrays.sort(),时间复杂度取决于快排O(n logn)
代码随想录
有序数组 [ -5 -3 1 3 5] 按从小到大排列,其平方之后两边一定是最大的,中间一定是最小的,所以定义双头指针,每次筛选出最大值,从新数组result的最大索引处填入。这样更新一轮下来,新数组就会从大到小填好。
定义双头指针比较出最大的元素有些像快速排序算法。
遇到问题
若先将元素更新为平方,然后再用于比较,那么这个元素如果这次尚未选中,下轮就会继续平方。所以这个判断逻辑应放到比较条件里。
代码
class Solution1 {public int[] sortedSquares(int[] nums) {int[] result = new int[nums.length];//定义新数组,大小应与原数组相同int left = 0;int right = nums.length - 1;//定义原数组双头指针int index = nums.length - 1;//定义填充新数组的索引指针for(;left<=right;){//left==right有意义应当进入循环if(nums[left]*nums[left]>nums[right]*nums[right]){result[index--] = nums[left]*nums[left];//若左边元素大,则复制给新数组,左边索引+1left++;}else{result[index--] = nums[right] * nums[right];//若右边元素大,则复制给新数组,右边索引-1;或者两边相同,则选谁填充都无所谓right--;}}return result;}
}209.长度最小的子数组
题目链接: 209. 长度最小的子数组 - 力扣(LeetCode)文章讲解:代码随想录
视频讲解:拿下滑动窗口! | LeetCode 209 长度最小的子数组_哔哩哔哩_bilibili
第一想法
首先一定是暴力想法,逐个数组遍历,若总和满足>=target,则记录数组长度,与上次符合要求的子数组结果作比较,若长度更小,则更新子数组。
代码随想录想法
用一个循环解决问题,那么j指的是子数组的终止位置,其起始位置的确定就在于滑动窗口的策略实现。如果指的是起始位置,那么只有一个一个向后遍历才能返回子数组,思路和暴力解法一致。
移动起始位置的条件是一旦当数组子数组之和>=target之后,起始指针就向后持续移动缩小数组。所以关键在于while循环而非if的单次判断。
一些录友会疑惑为什么时间复杂度是O(n)。
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
代码
class Solution1 {public int minSubArrayLen(int target, int[] nums) {int subLength = Integer.MAX_VALUE;int sum = 0;int beginIndex = 0;int endIndex = 0;for(;endIndex<nums.length;endIndex++){sum+=nums[endIndex];//终点指针持续向后移动while (sum>=target){subLength = Math.min(subLength, endIndex - beginIndex + 1);//更新最小长度sum -= nums[beginIndex++];//起始指针后移;}}return subLength == Integer.MAX_VALUE ? 0 : subLength;//若未赋值则返回0}
}59.螺旋矩阵
题目链接: 59. 螺旋矩阵 II - 力扣(LeetCode)文章讲解:代码随想录
视频讲解:一入循环深似海 | LeetCode:59.螺旋矩阵II_哔哩哔哩_bilibili
第一想法
没思路,一碰到循环和二维数组就寄
代码随想录思路
确定圈数:n/2,因为每转一圈,边长-2
n%2==1,有余数的话,最后一圈只要一个元素
每条边的处理都遵循左闭右开的原则,第一个节点留给此边处理,最后一个结点留给下一条边处理。
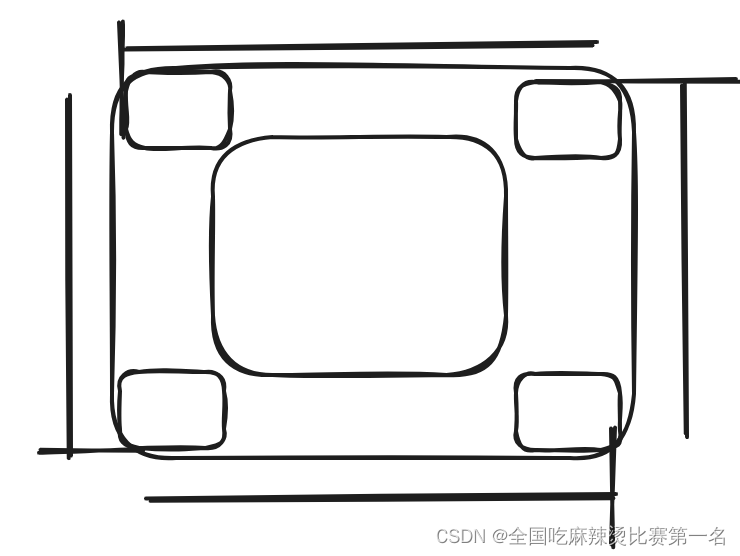
别人优化思路
1.关于中心元素处理:其实可以在初始化res矩阵的时候就直接把全部元素初始化为n*n,这样即使n是奇数,也无需处理中间的元素
2.startx,starty,offset可以优化成一个变量处理。
代码
画了一下四个边角的坐标,数组的边界处理,这个offset变量还是很难把握
class Solution {public int[][] generateMatrix(int n) {int[][] result = new int[n][n];//新建二维数组int loop = 0;int startX = 0, startY = 0, offset = 1;//起始X坐标,起始Y坐标,偏移量int count = 1;while (loop<n/2){int i = startX, j = startY;//先处理上边界for (j = startY; j < n - offset; j++) {//j的最大值应该是倒数第二个元素j<=n-1-offset,即j<n-offsetresult[startX][j] = count++;}//处理右边界for (i = startX; i < n - offset; i++) {//此时j等于n-offsetresult[i][j]=count++;}//处理下边界for(;j>startY;j--){result[i][j]=count++;}//处理左边界for(;i>startX;i--){result[i][j]=count++;}startX++;startY++;offset++;loop++;}if(n%2==1){result[startX][startY]=count;}return result;}
}相关文章:

代码随想录算法训练营第2天|LeetCode977,209,59
977.有序数组平方 题目链接: 977. 有序数组的平方 - 力扣(LeetCode) 文章讲解:代码随想录 视频讲解: 双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili 第一想法 暴力算法肯定是先将元素…...

Web前端开发——HTML快速入门
HTML:控制网页的结构CSS:控制网页的表现 一、什么是HTML、CSS (1)HTML (HyperText Markup Languaqe:超文本标记语言) 超文本:超越了文本的限制,比普通文本更强大。除了…...

浅谈http协议及常见的面试题
1、浅谈http协议 HTTP(Hypertext Transfer Protocol)超文本传输协议,是互联网上应用最为广泛的一种网络协议,所有的WWW文件都必须遵守这个标准。它是基于TCP/IP通信协议来传递数据(HTML文件、图片文件、查询结果等&am…...
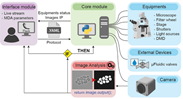
LabVIEW自动探头外观检测
开发了一套基于LabVIEW的软件系统,结合视觉检测技术,实现探头及连接器外观的自动检测。通过使用高分辨率工业相机、光源和机械手臂,系统能够自动定位并检测探头表面的细微缺陷,如划痕、残胶、异色、杂物等。系统支持多种探头形态&…...

搏击与防卫笔记
文章目录 降龙十八掌 咏春个人防身笔记防卫直拳应对耳光防卫摆拳坐马冲拳 本来想以武术为标题的,想了想武术这个标题太大太深,自己连一知半解都算不上,就谢为搏击与防卫吧。 每个男孩都有个武侠梦,独步江湖,仗剑走天涯…...
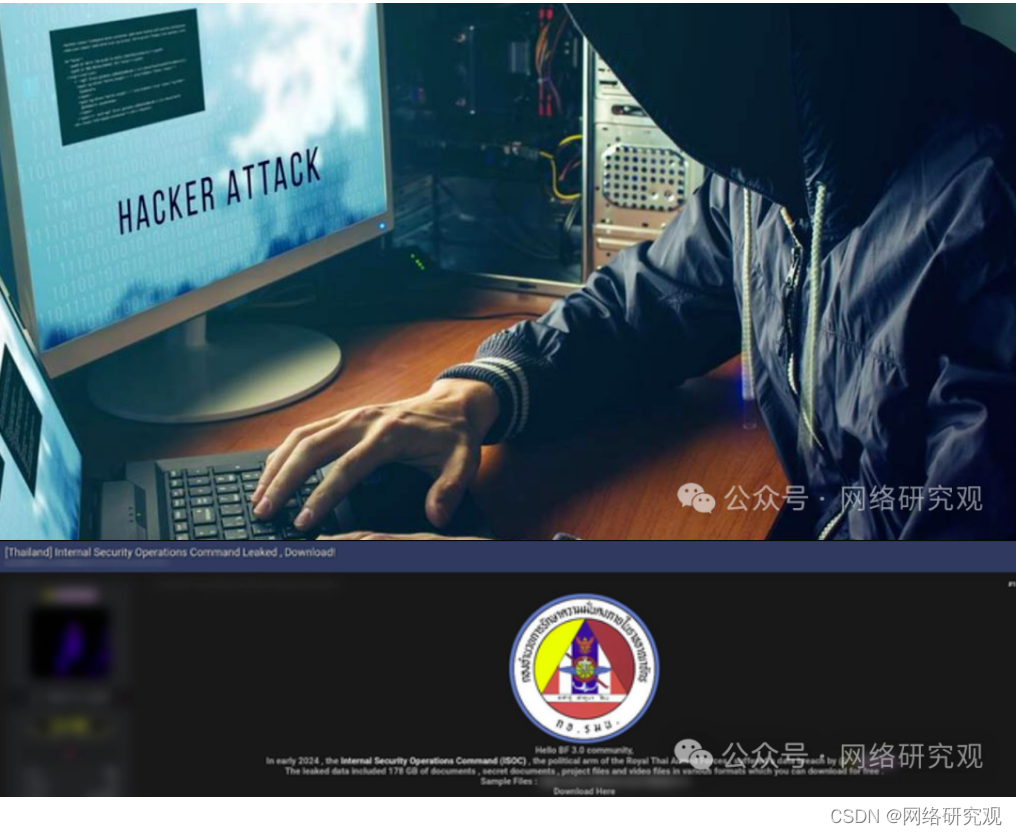
泰国内部安全行动司令部数据泄露
BreachForums 论坛的一名成员宣布发生一起重大数据泄露事件,涉及泰国内部安全行动司令部 (ISOC),该机构被称为泰国皇家武装部队的政治部门。 目前,我们无法准确确认此次泄露的真实性,因为该组织尚未在其网站上发布有关该事件的任…...
)
MATLAB算法实战应用案例精讲-【数模应用】分层聚类(附MATLAB、python和R语言代码实现)
目录 前言 几个高频面试题目 什么情况下选择分层聚类,什么情况下选择K-mean聚类呢?两种模型的好坏如何比较? 算法原理 SPSSAU 案例分析 SPSSPRO 1、作用 2、输入输出描述 3、案例示例 4、案例数据 5、案例操作 6、输出结果分析 7、注意事项 8、模型理论 分层…...

九、函数的声明和定义
函数声明: 1. 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数 声明决定不了。 2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。 3. 函数的声明一般要放在头文件中的。 定义的函…...
简洁纯文字类的Typecho主题wenso
主题介绍 文章说说类博客网站源码,页面清新简洁。适合文章说说美文博客网站建站使用,响应式手机版本。 本来是dedecms的模板,也比较简单,适合用来搭建一个文学类的,纯文字的网站,简单的改成了typecho&…...

安卓请求服务器[根据服务器的内容来更新spinner]
根据服务器的内容来更新spinner 本文内容请结合如下两篇文章一起看: 腾讯云函数node.js返回自动带反斜杠 腾讯云函数部署环境[使用函数URL] 现在有这样一个需求,APP有一个下拉选择框作为版本选择,因为改个管脚就变成一个版本,客户需求也很零散,所以后期会大量增加版本,这时候每…...
的特性和使用)
c++ 联合(Union)的特性和使用
联合(Union)是一种特殊的数据结构,允许在同一内存位置存储不同的数据类型。一个 union 可以有多个数据成员,但是在任意时刻只有一个数据成员可以有值。当某个成员被赋值后其他成员变为未定义状态。以下是联合的主要特点和使用方式…...
大白菜U盘启动工具
大白菜如何u盘启动进winpe装系统大白菜是一款非常实用的U盘启动盘制作工具,可以帮助用户快速地将U盘制作成启动盘,从而方便地进行系统安装、维护和修复等操作。官方网站: 大白菜u盘启动盘制作工具_大白菜u盘装系统_大白菜pe_大白菜官网-首页…...

C# 中 IEnumerable 和 IQueryable 接口之间的区别
在 C# 中,IEnumerable和IQueryable接口都用于查询数据集合,但它们的用途不同,功能也不同。下面是它们之间差异的细分: 1. C# 中的 IEnumerable 接口 在命名空间中定义System.Collections。表示集合中元素的只进式游标。适用于查…...

centos安装yum命令及常用yum命令
一、准备工作 获取安装介质: 如果你有CentOS的安装ISO文件或DVD介质,可以直接使用它来设置本地yum源。 如果没有,你需要在一个有网络连接的CentOS系统上下载所需的rpm包和依赖。 创建挂载点(如果你使用的是ISO文件)&a…...
申请的字典的类型是什么?)
table = collections.defaultdict(list)申请的字典的类型是什么?
当你使用 collections.defaultdict(list) 来申请一个字典时,这个字典的类型是 defaultdict,但是其行为和表现方式在某些方面与普通的字典(dict)相似,主要区别在于它如何处理缺失的键。 defaultdict 是 Python 标准库 …...

【虚拟机】虚拟机网络无法访问问题【已解决】
【虚拟机】虚拟机无法上网问题【已解决】 问题探究解决方法法1:查看相关“网络服务”是否处于正常启动状态法2:重启网络法3:重新安装VMWare法4:使用NAT模式,每次打开win7都没连上网的解决办法 问题探究 安装了很多个虚…...
)
大数据面试题之Spark(3)
目录 Spark的哪些算子会有shuffle过程? Spark有了RDD,为什么还要有Dataform和DataSet? Spark的RDD、DataFrame、DataSet、DataStream区别? Spark的Job、Stage、Task分别介绍下,如何划分? Application、job、Stage、task之间的关系 Stage内部逻辑…...

基于 Gunicorn + Flask + Docker 的模型高并发部署
在现代 Web 应用程序中,处理高并发请求是一个常见且重要的需求。本文将介绍如何使用 Gunicorn、Flask 和 Docker 来实现模型的高并发部署。我们将从环境设置、代码实现、Docker 镜像构建及部署等方面进行详细讲解。 一、环境设置 1. 安装 Flask 首先,…...
拉回, 交给GPU解码并显示的处理流程)
CPU通过网络将IP camera的RTSP流(H.264编码或是H.265编码)拉回, 交给GPU解码并显示的处理流程
这个流程涉及到从IP摄像头获取视频流(通过RTSP协议),然后将流传输给GPU进行解码和显示的过程。详细的流程描述如下: 1. 获取视频流: - **IP摄像头**: 摄像头通过RTSP(Real-Time Streaming Protocol)将…...
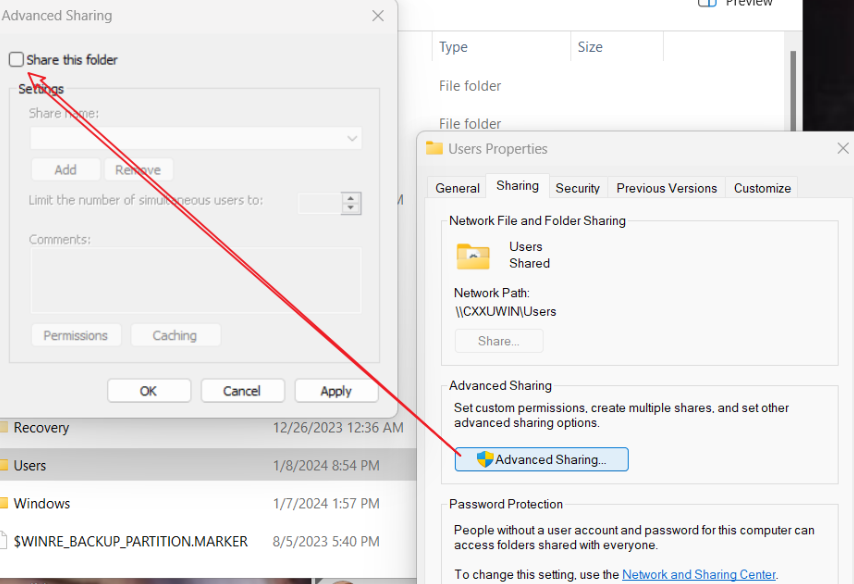
windows@资源管理器中的地址栏@访问共享文件夹的各种方法@管理共享文件夹
文章目录 资源管理器中的地址栏可以访问什么访问共享文件夹👺UNC路径资源管理器打开共享文件夹纯命令行方式访问共享文件夹 共享文件夹相关操作查看所有已经共享的文件夹👺停止某个文件的共享 共享文件夹的访问控制补充匿名访问问题😊强制启用…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...
个人电脑部署本地大模型+UI
在这个AI飞速进步的时代,越来越多的大模型出现在市面上 本地大模型也越来越火爆! 它完全免费,随时可以访问,数据仅存在本地,还可以自己微调,训练! 今天我来教大家,如何在一台普通…...
