【LeetCode:841. 钥匙和房间 + DFS】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域优质创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |


🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ DFS
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 💬 共勉
🚩 题目链接
- 841. 钥匙和房间
⛲ 题目描述
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]]
输出:true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。
提示:
n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <= sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同
🌟 求解思路&实现代码&运行结果
⚡ DFS
🥦 求解思路
- 该题通过DFS或者BFS来实现,从0位置开始,去找到可以从当前list.get(0)集合中所有可去向的房间,如果当前位置没有走过,计数加1。递归结束后,判断此时cnt和房间的个数是否相等,如果相等,返回true,否则返回false。
- 有了基本的思路,接下来我们就来通过代码来实现一下递归和迭代的解法。
🥦 实现代码
class Solution {List<List<Integer>> rooms;boolean[] flag;int cnt;int n;public boolean canVisitAllRooms(List<List<Integer>> rooms) {this.rooms = rooms;this.flag = new boolean[rooms.size()];this.cnt = 0;dfs(0);return cnt == rooms.size();}private void dfs(int i) {cnt++;flag[i] = true;for (int next : rooms.get(i)) {if (!flag[next])dfs(next);}}}
🥦 运行结果
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【LeetCode:841. 钥匙和房间 + DFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
并发事务的问题)
1)并发事务的问题
1) 并发事务的问题? (1)读“脏”数据 事务T1修改数据后T2读取了该数据,但是T1撤消了修改, 事务T1进行了回滚,导致事务T2读取的数据与数据库中的数据不一致。(2)丢失修改 两个事务…...

Python缓存利器:cachetools库详解
Python缓存利器:cachetools库详解 1. cachetools简介2. 安装3. 基本概念3.1 LRU Cache (Least Recently Used)3.2 TTL Cache (Time-To-Live)3.3 LFU Cache (Least Frequently Used) 4. 使用示例4.1 使用LRU Cache4.2 使用TTL Cache4.3 使用LFU Cache4.4 缓存装饰器 5. 进阶用法…...
【Python实战因果推断】20_线性回归的不合理效果10
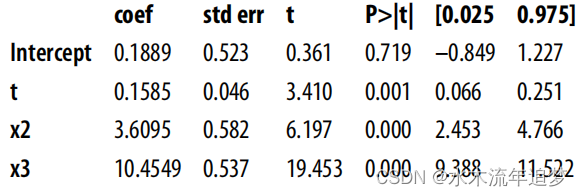
目录 Neutral Controls Noise Inducing Control Feature Selection: A Bias-Variance Trade-Off Neutral Controls 现在,您可能已经对回归如何调整混杂变量有了一定的了解。如果您想知道干预 T 对 Y 的影响,同时调整混杂变量 X,您所要做的…...

在Ubuntu 16.04上安装和配置ownCloud的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 ownCloud 是一个文件共享服务器,允许您将个人内容(如文档和图片)存储在一个类似 Dropbox 的集…...

Java | Leetcode Java题解之第213题打家劫舍II
题目: 题解: class Solution {public int rob(int[] nums) {int length nums.length;if (length 1) {return nums[0];} else if (length 2) {return Math.max(nums[0], nums[1]);}return Math.max(robRange(nums, 0, length - 2), robRange(nums, 1,…...

使用 ESP32 接收 MAX4466 模拟麦克风模块的数据,通过 DAC 转码成 PCM 格式,并通过 MQTT 发送给另一台设备,可以通过以下步骤实现。
硬件准备 两个 ESP32 开发板MAX4466 模拟麦克风模块MQTT 服务器(例如 Mosquitto) 接线 MAX4466 模块输出(AO) -> ESP32 ADC 引脚(如 GPIO 34) 软件准备 音频采集DAC 转码MQTT 发送和接收 代码实现…...
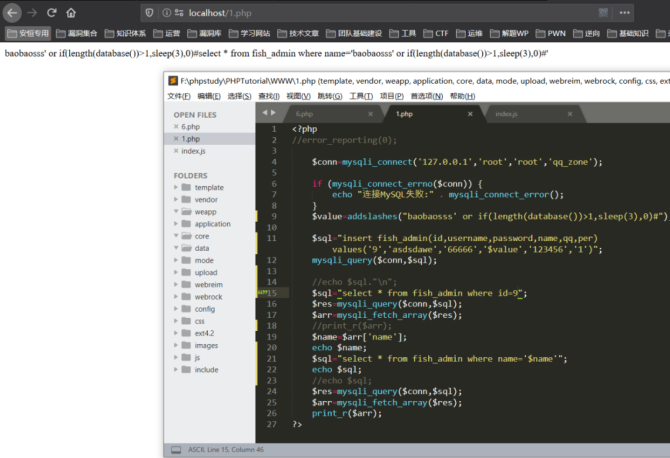
SQL二次注入原理分析
二次注入在测试的时候比较少见,或者说很难被测出来,因为测的时候首先要去找注入的位置,其次是去判断第一次执行的SQL语句,然后还要去判断第二次进行调用的 SQL 语句。而关键问题就出在第二次的调用上面。 下面以一个常用过滤方法…...
在线签约如何选择?2024年10款顶级app大比拼
支持电子合同签约的10大app:e签宝、上上签、DocuSign、契约锁、Adobe Sign、法大大、SignNow、安心签、HelloSign、PandaDoc。 无论是企业之间的交易还是个人服务合同,线上电子合同签约提供了一种便捷、高效且安全的方式来处理法律文档。本文将介绍几款优…...

gcc: warning: -Wunused-function;加了选项,为什么就不报警告呢?
文章目录 问题clang的编译而使用gcc是就不报问题分析原因如果是非static的函数问题 下面这个代码段,其中这个函数hton_ext_2byte,在整个程序里就没有使用。 static inline uint16_t hton_ext_2byte(uint8_t **p) {uint16_t v;******return v;...

系统提示我未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘finverse‘,如何解决?
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...

【电路笔记】-B类放大器
B类放大器 文章目录 B类放大器1、概述2、B类放大器介绍3、推挽式配置4、限制交叉失真5、B类放大器效率6、总结1、概述 我们在之前的文章中已经知道,A 类放大器的特点是导通角为 360,理论最大效率为 50%。 在本文中,我们将详细介绍另一类放大器,称为B类放大器,它是为解决A…...
Ubuntu 22.04 安装中文字体
笔者在用OpenCV4.9处理图片加水印时,中文乱码。原来是Ubuntu 22.04发行版缺少中文字体支持,因此,笔者就找资料安装了需要的中文字体,特此记录,以备后查。 1、打开终端: 2、更新软件包列表: su…...

「树莓派入门」树莓派进阶04-直流电机控制与PWM应用
直流电机控制是树莓派硬件项目中的一项重要技能。通过PWM技术,你可以实现对电机速度的精确控制。在实验过程中,请注意电机的电源匹配和GPIO引脚的保护。 一、直流电机基本原理 直流电机通过直流电源供电,其工作原理基于洛伦兹力定律,即电流通过线圈时,会在磁场中受到力的…...

利用数据集,用机器学习模型对股市预测,聊聊看!
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...

015-GeoGebra基础篇-定点旋转物体、动态显示数值并显示运动轨迹
这可能是我能想到的最大概率可以被你搜索到的标题了,容我先喘口气~ 目录 一、成品展示二、涉及内容三、做图步骤(1)绘制三角形t(2)建立定点D(3)制作角度滑动条(4)图形绕点…...

2024年6月份找工作和面试总结
转眼间6月份已经过完了,2024年已经过了一半,希望大家都找到了合适的工作。 本人前段时间写了5月份找工作的情况,请查看2024年5月份面试总结-CSDN博客 但是后续写的总结被和谐了,不知道这篇文章能不能发出来。 1、6月份面试机会依…...

同步时钟:北斗/GPS卫星、电信基站、NTP以太网校时方式的区别
同步时钟是保证各设备时间统一的重要装置,广泛应用于电力、通信、金融、学校、医院、地铁等多个领域。目前,常用的同步时钟方式包括:北斗/GPS卫星、电信基站、NTP以太网等。 下面跟着小编来看一下这些校时方式及他们的区别吧。 1. 北斗/GP…...

实现Java应用的快速开发与迭代
实现Java应用的快速开发与迭代 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. 引言 随着软件开发周期的不断缩短和市场竞争的加剧,快速开发和…...
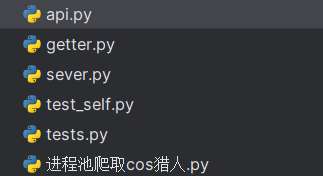
利用redis数据库管理代理库爬取cosplay网站-cnblog
爬取cos猎人 数据库管理主要分为4个模块,代理获取模块,代理储存模块,代理测试模块,爬取模块 cos猎人已经倒闭,所以放出爬虫源码 api.py 为爬虫评分提供接口支持 import requests import concurrent.futures import …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
