【算法 - 哈希表】两数之和
这里写自定义目录标题
- 两数之和
- 题目解析
- 思路
- 解法一 :暴力枚举 依次遍历
- 解法二 :使用哈希表来做优化
- 核心逻辑
- 为什么之前的暴力枚举策略不太好用了?
- 所以,这就是 这道题选择 ==固定一个数,再与其前面的数逐一对比完后,再将其自身放入hash表中,参与匹配== 的原因
- 代码实现
两数之和
题目解析

思路
解法一 :暴力枚举 依次遍历
- 时间复杂度 O(n^2)
暴力枚举两层for()循环遍历O(n^2) - 空间复杂度 无
- 先固定其中一个数
- 依次与该数之前的数相加
而 解法二 则是,遍历完这个数以后,将其丢入hash表中。枚举下一个数时,很自然的枚举hash表中前面遍历过的数
解法二 :使用哈希表来做优化
-
时间复杂度:O(n)
由原来的 暴力枚举两层for()循环遍历O(n^2) 到 ,只需遍历一遍 固定一个数O(n),哈希表查找匹配的另一个数O(1) -
空间复杂度:O(n)
对比 暴力枚举 即可看出,哈希表是用 空间换时间
核心逻辑
为什么之前的暴力枚举策略不太好用了?
我们也能把所有的数都放入hash表中,再由前往后遍历一遍数组,再直接在hash中找匹配的数就好了,为什么还要 逐一遍历,再将遍历到的节点逐一放入hash表中 ?
这是因为会出现 “恰好 遍历到的数本身,也能满足匹配的要求” 的情况,这违反了题目所说的需求 数组中同一个元素在答案里不能重复出现
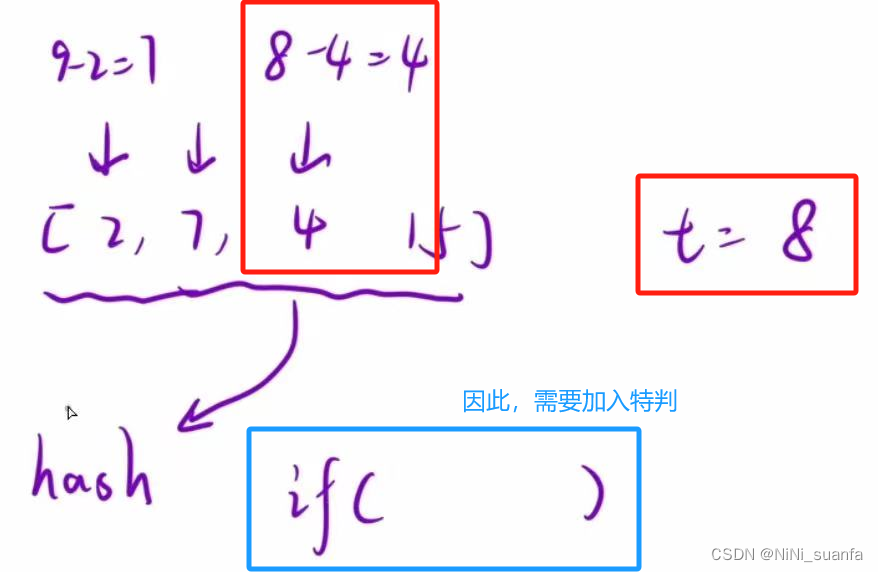
blog.csdnimg.cn/direct/4e384c8f2ebd454f910606e12c610d2c.jpeg)
因此,这种做法需要加入特判。
所以,这就是 这道题选择 固定一个数,再与其前面的数逐一对比完后,再将其自身放入hash表中,参与匹配 的原因
因此,循环遍历固定一个节点,遍历完后将该节点放入hash表中,后继续向后遍历,仅需查找前面放入hash表中的值即可(就不会出现查找hash表中选中自身的情况),这样的顺序避免了 出现了重复出现同一个数字 的情况 。也 不需要再处理什么边界情况 了。
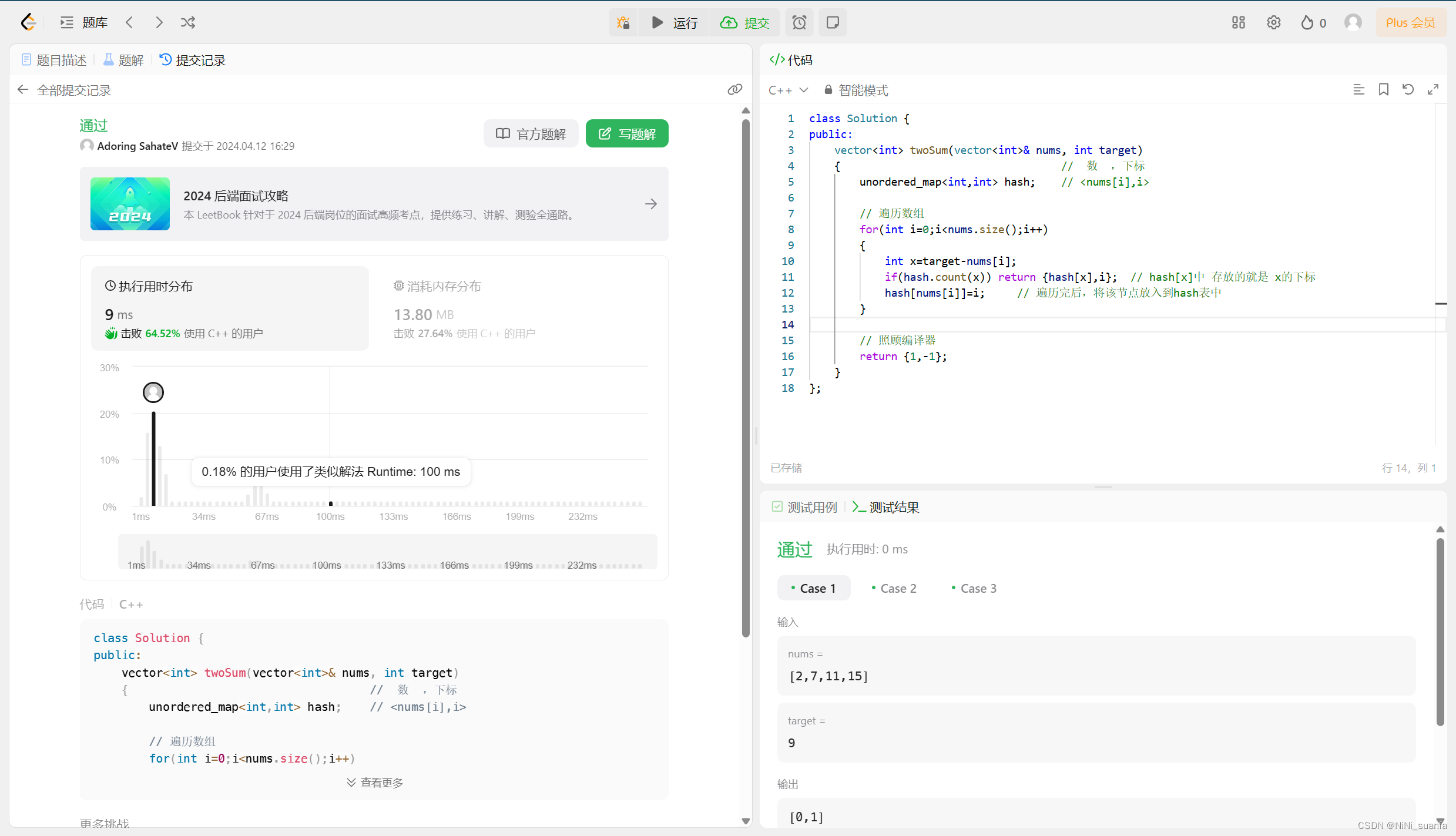
代码实现
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) { // 数 ,下标unordered_map<int,int> hash; // <nums[i],i> // 遍历数组for(int i=0;i<nums.size();i++){int x=target-nums[i];if(hash.count(x)) return {hash[x],i}; // hash[x]中 存放的就是 x的下标hash[nums[i]]=i; // 遍历完后,将该节点放入到hash表中}// 照顾编译器return {1,-1};}
};
相关文章:

【算法 - 哈希表】两数之和
这里写自定义目录标题 两数之和题目解析思路解法一 :暴力枚举 依次遍历解法二 :使用哈希表来做优化 核心逻辑为什么之前的暴力枚举策略不太好用了?所以,这就是 这道题选择 固定一个数,再与其前面的数逐一对比完后&…...
:线性回归模型第一部分:认识线性回归模型)
【深度学习】图形模型基础(5):线性回归模型第一部分:认识线性回归模型
1. 回归模型定义 最简单的回归模型是具有单一预测变量的线性模型,其基本形式如下: y a b x ϵ y a bx \epsilon yabxϵ 其中, a a a 和 b b b 被称为模型的系数或更一般地,模型的参数。 ϵ \epsilon ϵ 代表误差项&#…...

2024 年第十四届 APMCM 亚太地区大学生数学建模竞赛B题超详细解题思路+数据预处理问题一代码分享
B题 洪水灾害的数据分析与预测 亚太中文赛事本次报名队伍约3000队,竞赛规模体量大致相当于2024年认证杯,1/3个妈杯,1/10个国赛。赛题难度大致相当于0.6个国赛,0.8个妈杯。该比例仅供大家参考。 本次竞赛赛题难度A:B:C3:1:4&…...

Yarn有哪些功能特点
Yarn是一个由Facebook团队开发,并联合Google、Exponent和Tilde等公司推出的JavaScript包管理工具,旨在提供更优的包管理体验,解决npm(Node Package Manager)的一些痛点。Yarn的功能特点主要包括以下几个方面࿱…...

深度学习算法bert
bert 属于自监督学习的一种(输入x的部分作为label) 1. bert是 transformer 中的 encoder ,不同的bert在encoder层数、注意力头数、隐藏单元数不同 2. 假设我们有一个模型 m ,首先我们为某种任务使用大规模的语料库预训练模型 m …...

PyTorch - 神经网络基础
神经网络的主要原理包括一组基本元素,即人工神经元或感知器。它包括几个基本输入,例如 x1、x2… xn ,如果总和大于激活电位,则会产生二进制输出。 样本神经元的示意图如下所述。 产生的输出可以被认为是具有激活电位或偏差的加权…...
docker-compose搭建minio对象存储服务器
docker-compose搭建minio对象存储服务器 最近想使用oss对象存储进行用户图片上传的管理,了解了一下例如aliyun或者腾讯云的oss对象存储服务,但是呢涉及到对象存储以及经费有限的缘故,决定自己手动搭建一个oss对象存储服务器; 首先…...

vue3使用pinia中的actions,需要调用接口的话
actions,需要调用接口的话,假如页面想要调用actions中的方法获取数据, 必须使用try catch async await 进行包裹,详情看下面代码 import {defineStore} from pinia import {reqCode,reqUserLogin} from ../../api/hospital/i…...

Python酷库之旅-第三方库Pandas(003)
目录 一、用法精讲 4、pandas.read_csv函数 4-1、语法 4-2、参数 4-3、功能 4-4、返回值 4-5、说明 4-6、用法 4-6-1、创建csv文件 4-6-2、代码示例 4-6-3、结果输出 二、推荐阅读 1、Python筑基之旅 2、Python函数之旅 3、Python算法之旅 4、Python魔法之旅 …...

社交电商中的裂变营销利器,二级分销模式,美妆家具成功案例分享
二级分销返佣模式是一种帮助商家迅速扩大市场覆盖的有效营销策略,不仅能降低营销成本,还能提升品牌知名度。下面通过两个具体的案例来说明这种模式的好处和优势。 某知名美妆品牌在市场竞争日益激烈的情况下,决定采用二级分销返佣模式进行市场…...

【国产开源可视化引擎Meta2d.js】图层
独立图层 每个图元都有先后绘画顺序,即每个图元拥有一个独立图层,即meta2d.data().pens的数组索引。 可以通过meta2d.top/bottom/up/down等函数改变独立图层顺序。 分组图层 通过标签可以标识一个分组图层,通过meta2d.find(图层标签)获取…...

基于Redisson实现分布式锁
基于redisson实现分布式锁 之前背过分布式锁几种实现方案的八股文,但是并没有真正自己实操过。现在对AOP有了更深一点的理解,就自己来实现一遍。 1、分布式锁的基础知识 分布式锁是相对于普通的锁的。普通的锁在具体的方法层面去锁,单体应…...

Android Studio下载Gradle特别慢,甚至超时,失败。。。解决方法
使用Android studio下载或更新gradle时超级慢怎么办? 切换服务器,立马解决。打开gradle配置文件 修改服务器路径 distributionUrlhttps\://mirrors.cloud.tencent.com/gradle/gradle-7.3.3-bin.zip 最后,同步,下载,速…...
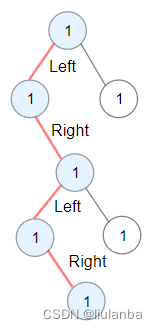
leetcode--二叉树中的最长交错路径
leetcode地址:二叉树中的最长交错路径 给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下: 选择二叉树中 任意 节点和一个方向(左或者右)。 如果前进方向为右,那么移动到当前节点的的右子节点&…...

c++ primer plus 第15章友,异常和其他:15.1.3 其他友元关系
c primer plus 第15章友,异常和其他:15.1.3 其他友元关系 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 15.1.3 其他友元关系 提示:写完文章后,目录可以自动生成,如何生成可…...

uniapp+vue3页面跳转和传参
页面跳转: uni.navigateTo({url: /pages/index}) 返回上一层: uni.navigateBack ({delta: 1 }) 页面跳转时传参: 跳转前的页面: uni.navigateTo({url: "/pages/index?id123"}) 跳转后的页面: onLoa…...

硬链接和软链接
在Linux系统中,链接(Link)是一种特殊的文件,它指向另一个文件或目录。链接分为两种类型:硬链接(Hard Link)和软链接(也称为符号链接,Symbolic Link)。 1. 硬…...
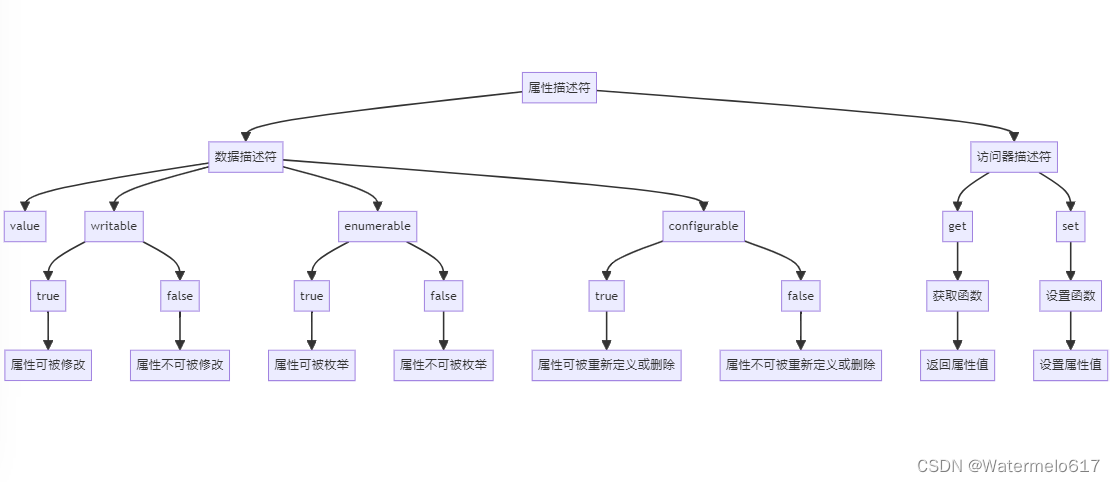
属性描述符初探——Vue实现数据劫持的基础
目录 属性描述符——Vue实现数据劫持的基础 一、属性描述符是什么? 编辑 1.1、属性描述符示例 1.2、用属性描述符定义属性及获取对象的属性描述符 1.3、带有读取器和设置器的属性描述符 二、使用属性描述符的情景 2.1、封装和数据隐藏 使用getter和setter…...

字节也没余粮了?天底下没有永远免费的GPT-4;AI产品用订阅制就不合理!让用户掏钱的N种定价技巧嘿嘿 | ShowMeAI日报
👀日报&周刊合集 | 🎡ShowMeAI官网 | 🧡 点赞关注评论拜托啦! 1. 当 Coze 也开始收费:天底下没有「永远」免费的 GPT-4 注:这里 Coze 指海外版。国内版 扣子 还是免费。 Coze (海外版) 官网链接 → htt…...

【Matlab 路径优化】基于蚁群算法的XX市旅游景点线路优化系统
基于蚁群算法的XX市旅游景点线路优化系统 (一)客户需求: ①考虑旅游景点的空间分布、游客偏好等因素,实现了旅游线路的智能规划 ②游客选择一景点出发经过所要游览的所有景点只一次,最后回到出发点的前提下…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
