数字信号处理及MATLAB仿真(2)——离散系统
上回书说到如何来编写一些简单的离散时间序列,今天咱们就来谈谈一些关于常系数差分方程的操作吧。
说到这里咱们对于常系数差分方程可能最关心的就是怎么去求解了。
其中最关键的部分就是filter函数,可以用来计算系统在输入信号为x的输出信号y。大家学过这个函数的可能会有个疑问——filter函数不是一个用来滤波函数吗?对于这个我只能说问的好。因为答案往往就在疑问的背后,其实filter函数的具体工作原理是基于差分方程的数学运算。它根据输入信号x以及系数向量a和b,按照差分方程的规则逐步计算输出信号y的每个样本值。在计算过程中,会考虑输入信号的当前和过去样本值,以及输出信号的过去样本值,以得到符合差分方程关系的输出结果。这种计算方式能够模拟离散系统对输入信号的响应。需要注意的是,在使用filter函数时,要确保a向量的第一个元素不为零,否则需要对b和a的元素进行相应的处理。
来看两个例子吧。一个是一阶的方程求解,还有一个是二阶方程的求解。程序如下。
%差分方程的求解
%差分方程为y[n]-0.5y[n-1]=x[n]。
clear all
clc
% 定义差分方程系数
a = [1, -0.5]; % y[n] 的系数
b = 1; % x[n] 的系数
% 生成输入信号 x[n](这里用正弦波示例)
n = 0:99;
x = sin(2*pi*0.1*n);
% 使用 filter 函数求解差分方程
y = filter(b, a, x);
% 绘制输入信号和输出信号
figure;
subplot(2,1,1);
plot(n, x);
xlabel('n');
ylabel('x[n]');
title('输入信号');
subplot(2,1,2);
plot(n, y);
xlabel('n');
ylabel('y[n]');
title('输出信号');
% 显示差分方程
disp('差分方程:');
disp('y[n] - 0.5y[n-1] = x[n]');
%%
% 定义差分方程系数
a = [1, -1.5, 0.7]; % y[n] 的系数
b = [1, 0.5]; % x[n] 的系数
% 生成输入信号 x[n](这里用正弦波示例)
n = 0:99;
x = sin(2*pi*0.1*n);
% 使用 filter 函数求解差分方程
y = filter(b, a, x);
% 绘制输入信号和输出信号
figure;
subplot(2,1,1);
plot(n, x);
xlabel('n');
ylabel('x[n]');
title('输入信号');
subplot(2,1,2);
plot(n, y);
xlabel('n');
ylabel('y[n]');
title('输出信号');
% 显示差分方程
disp('差分方程:');
disp('y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]');
运行结果:


结果大概就这样了,大家细细比较还是有那么点区别。但是具体一点的区别,大家可以用双零分解的方法去求求,验证一下,理论和实际之间还是有区别的。
接下来看看,单位冲激响应怎么搞,核心是impz函数,在 MATLAB 中,impz函数用于计算并返回数字滤波器的单位冲激响应。差分方程为y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1],程序如下图。
%单位冲激响应
%差分方程为y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]
% 定义差分方程系数
a = [1, -1.5, 0.7]; % y[n] 的系数
b = [1, 0.5]; % x[n] 的系数
% 计算单位冲激响应
[h, n] = impz(b, a);
% 绘制单位冲激响应
figure;
stem(n, h);
xlabel('n');
ylabel('h[n]');
title('单位冲激响应');
grid on;
% 显示差分方程
disp('差分方程:');
disp('y[n] - 1.5y[n-1] + 0.7y[n-2] = x[n] + 0.5x[n-1]');
首先,定义了差分方程中与y[n] 的系数 a 和 x[n] 的系数 b 。然后,使用 impz函数计算单位冲激响应 h以及对应的时间索引 n。接下来,通过 stem函数绘制单位冲激响应的图形xlabel 和 ylabel 分别设置了横纵坐标的标签,title 给出了图形的标题,grid on 显示网格。最后,使用 disp 函数显示了定义的差分方程。运行这段代码,将会得到单位冲激响应的图形。结果如下图所示。

今天主要讲的就是离散时间系统,结合例子理解更加的合适。
欲知后事如何,且听下回分解。OVO........
相关文章:

数字信号处理及MATLAB仿真(2)——离散系统
上回书说到如何来编写一些简单的离散时间序列,今天咱们就来谈谈一些关于常系数差分方程的操作吧。 说到这里咱们对于常系数差分方程可能最关心的就是怎么去求解了。 其中最关键的部分就是filter函数,可以用来计算系统在输入信号为x的输出信号y。大家学过…...
技术原理)
大模型思维链(Chain-of-Thought)技术原理
大模型思维链(Chain-of-Thought)技术原理 NLP中 大语言模型LLM中的思维链 Chain-of-Thought(CoT) GoT_cot思维链-CSDN博客 https://zhuanlan.zhihu.com/p/680618940 https://zhuanlan.zhihu.com/p/661475269...
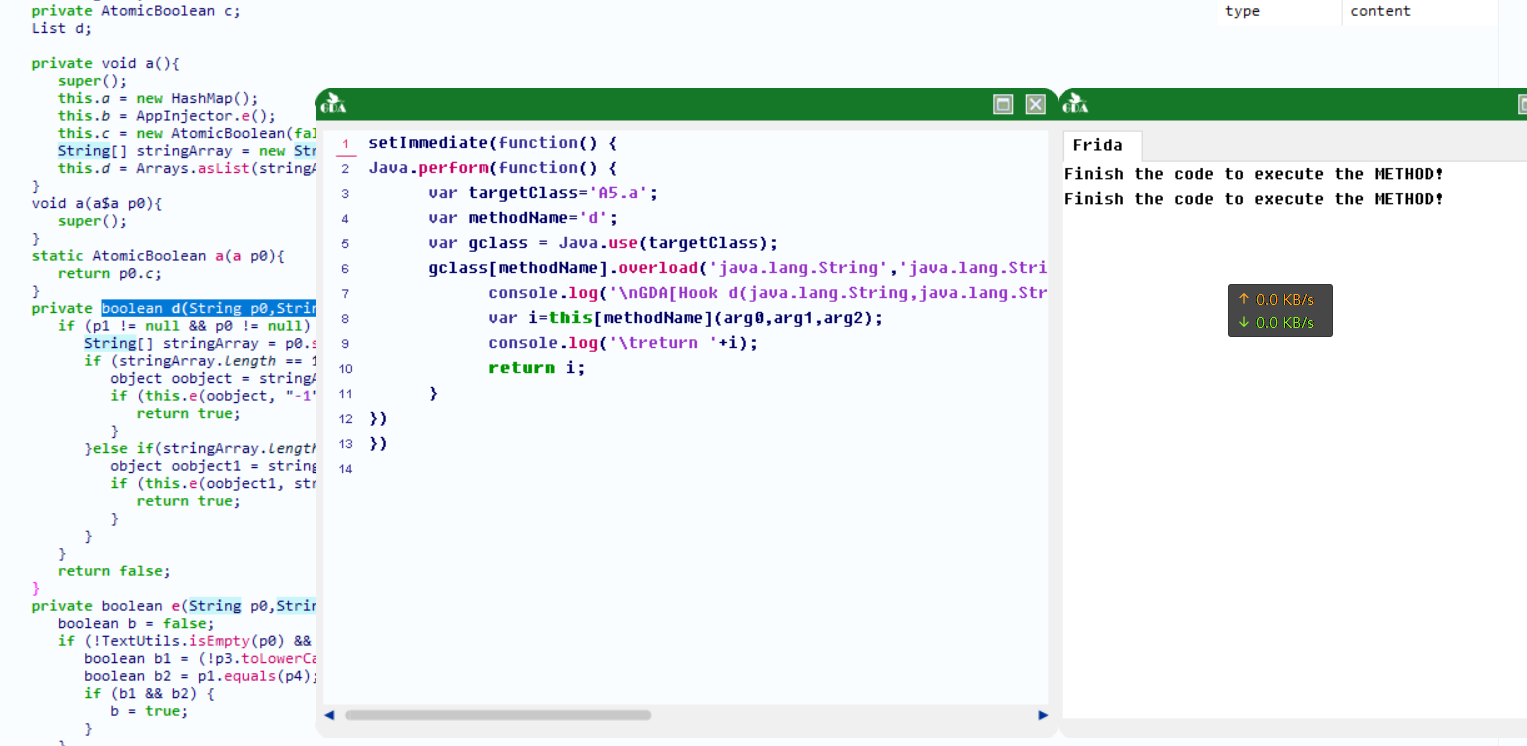
gda动态调试-cnblog
忽的发现gda有动态调试功能 动态监听返回值 框柱指定方法,选择调试方法,gda会自动监听函数的返回值,例如 自定义frida脚本 gda会自动生成hook该函数的frida脚本...

Double 4 VR仿真情景实训教学系统在法律专业课堂上的应用
随着科技的飞速发展,VR技术逐渐渗透到各个领域,为教育行业带来了革命性的变化。 VR技术以其独特的沉浸式体验,为法律课堂带来了前所未有的学习体验。通过Double 4 VR仿真情景实训教学系统,学生可以身临其境地进入虚拟的仿真情景中…...

k8s-第一节-minikube
minikube 服务器启动 # 启动集群 minikube start # 启动集群并使用docker驱动 minikube start --driverdocker To make docker the default driver:minikube config set driver docker # 查看节点。kubectl 是一个用来跟 K8S 集群进行交互的命令行工具 kubectl get node # 停…...

html+js+css在线倒计时
代码在图片后面 点赞加关注 谢谢大佬照顾😜 图例 时间到前 时间到后 源代码 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width,…...

构建LangChain应用程序的示例代码:55、如何实现多代理模拟,其中特权代理决定谁发言。这遵循与多代理分散发言者选择相反的选择方案
示例展示了如何实现一个多代理模拟,其中一个特权代理决定谁来发言。 这遵循与多代理分散式发言人选择相反的选择方案。 我们在一个虚构的新闻网络模拟环境中展示这种方法的一个例子。这个例子将展示我们如何实现能够: 在说话前思考终止对话 的代理。 导入LangChain相关模块…...

船舶雷达与导航系统选择7/8防水插座的原因分析
概述 船舶雷达与导航系统在现代航海中扮演着至关重要的角色,它们为船舶提供准确的导航信息,确保航行的安全和效率。在这些系统中,7/8防水插座的使用尤为重要,因为它们能够在恶劣的海上环境中提供稳定的电力和信号连接。接下来&am…...

墨烯的C语言技术栈-C语言基础-006
六.常量 C语言的常量为 字面常量 const修饰的常变量 #define定义的 枚举常量 int main() { // 四个都是字面常量 30; 3.14; "w"; // 字符常量 "abc"; // const修饰的常变量 const int a 10; // 在C语言中,const修饰的a,本质是变量,但不能直…...

常用SHELL命令
在 Unix/Linux 系统中,除了基本的文件和目录操作命令外,还有许多强大的工具命令,用于文本处理、系统监控、文件操作等。以下是一些常用的 Shell 命令,特别是类似 sed 和 awk 的文本处理工具: 文本处理命令 sed - 流编…...

Python脚本:将Word文档转换为Excel文件
引言 在文档处理中,我们经常需要将Word文档中的内容转换成其他格式,如Excel,以便更好地进行数据分析和报告。针对这一需求,我编写了一个Python脚本,能够批量处理指定目录下的Word文档,将其内容结构化并转换…...

【单链表】03 设L为带头结点的单链表,编写算法实现从尾到头反向输出每个结点的值。
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux算法题上机准备 😘欢迎 ❤️关注 👍点赞 🙌收藏 ✍️留言 题目 设L为带头结点的单链表,编写算法实现从尾到头反向输出每个结点的值。 算法…...
鸿蒙开发设备管理:【@ohos.vibrator (振动)】
振动 说明: 开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 导入模块 imp…...

【信息学奥赛】CSP-J/S初赛07 排序算法及其他算法在初赛中的考察
本专栏👉CSP-J/S初赛内容主要讲解信息学奥赛的初赛内容,包含计算机基础、初赛常考的C程序和算法以及数据结构,并收集了近年真题以作参考。 如果你想参加信息学奥赛,但之前没有太多C基础,请点击👉专栏&#…...

第N7周:seq2seq翻译实战-pytorch复现-小白版
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 理论基础 seq2seq(Sequence-to-Sequence)模型是一种用于机器翻译、文本摘要等序列转换任务的框架。它由两个主要的递归神经网络&#…...

java集合(1)
目录 一.集合概述 二. 集合体系概述 1. Collection接口 1.1 List接口 1.2 Set接口 2. Map接口 三. ArrayList 1.ArrayList常用方法 2.ArrayList遍历 2.1 for循环 2.2 增强for循环 2.3 迭代器遍历 一.集合概述 我们经常需要存储一些数据类型相同的元素,之前我们学过…...
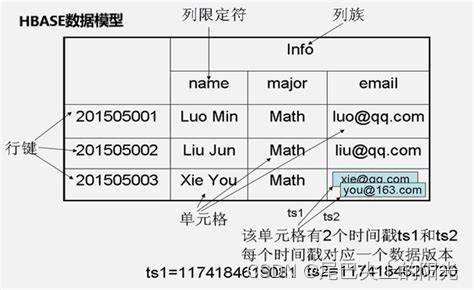
分布式数据库HBase:从零开始了解列式存储
在接触过大量的传统关系型数据库后你可能会有一些新的问题: 无法整理成表格的海量数据该如何储存? 在数据非常稀疏的情况下也必须将数据存储成关系型数据库吗? 除了关系型数据库我们是否还有别的选择以应对Web2.0时代的海量数据? 如果你也曾经想到过这些问题, 那么HBase将是…...

接口测试流程及测试点!
一、什么时候开展接口测试 1.项目处于开发阶段,前后端联调接口是否请求的通?(对应数据库增删改查)--开发自测 2.有接口需求文档,开发已完成联调(可以转测),功能测试展开之前 3.专…...
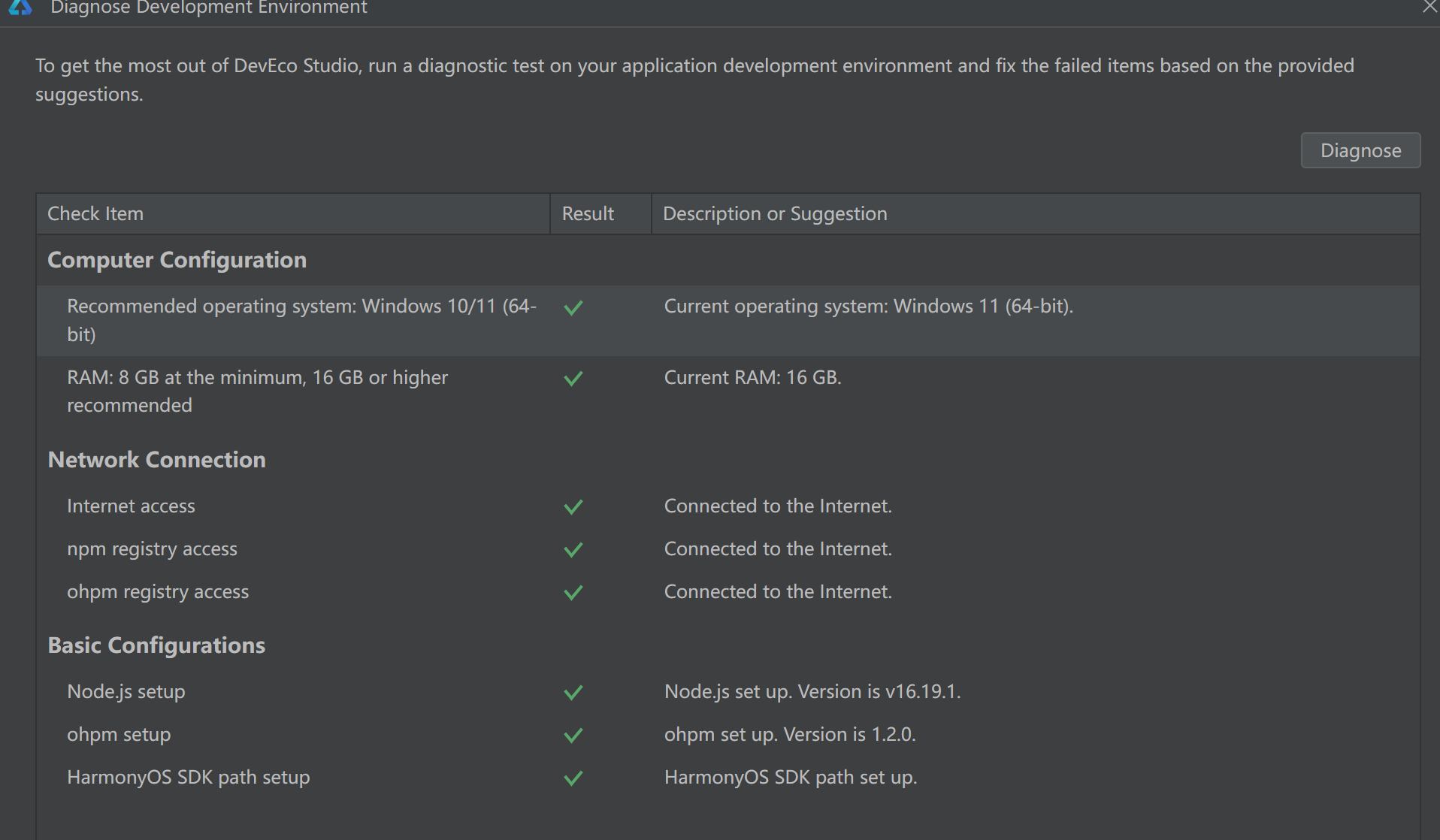
已经安装deveco-studio-4.1.3.500的基础上安装deveco-studio-3.1.0.501
目录标题 1、执行exe文件后安装即可2、双击devecostudio64_3.1.0.501.exe2.1、安装Note (注意和4.1的Note放不同目录)2.2、安装ohpm (注意和4.1版本的ohpm放不同目录)2.3、安装SDK (注意和4.1版本的SDK放不同目录) 1、执行exe文件后安装即可 2、双击devecostudio64_3.1.0.501.e…...

【C++】 解决 C++ 语言报错:Use of Uninitialized Variable
文章目录 引言 使用未初始化的变量(Use of Uninitialized Variable)是 C 编程中常见且危险的错误之一。它通常在程序试图使用尚未赋值的变量时发生,导致程序行为不可预测,可能引发运行时错误、数据损坏,甚至安全漏洞。…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
