基于GWO灰狼优化的多目标优化算法matlab仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1灰狼优化算法原理
4.2 多目标优化问题(MOP)的帕累托最优解
4.3 基于GWO的多目标优化算法
5.完整程序
1.程序功能描述
基于GWO灰狼优化的多目标优化算法matlab仿真,目标函数为2个目标函数。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
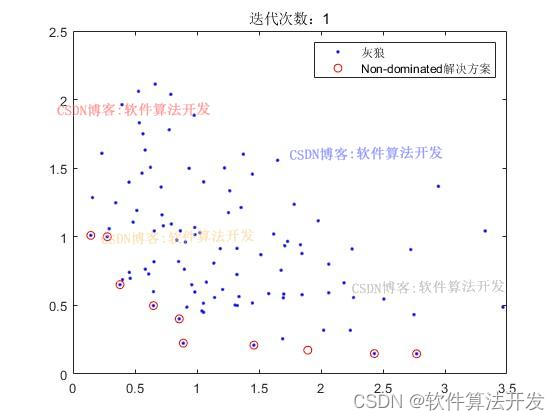
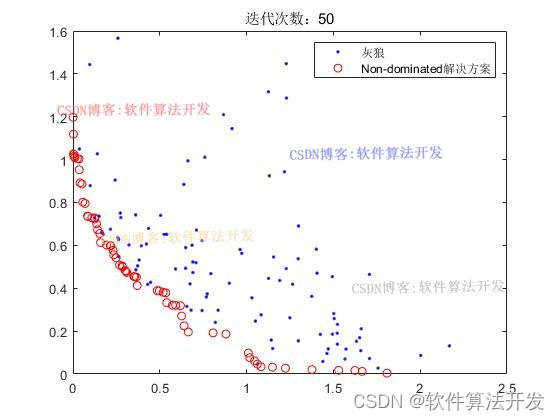
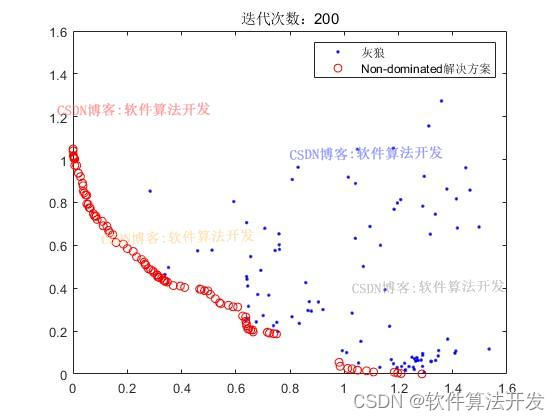
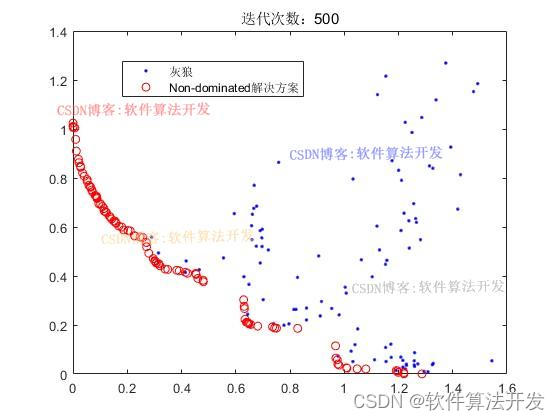
迭代1000次:

(完整程序运行后无水印)
3.核心程序
.......................................................................
% MOGWO(多目标灰狼优化)主循环
for it=1:Mitersit% 更新支配关系并获取非支配解集GWO0=func_domination(GWO0);GWO0n=func_Nondomination(GWO0);% 更新存档并执行非支配排序GWO1=[GWO1GWO0n];GWO1=func_domination(GWO1);GWO1=func_Nondomination(GWO1);% 重新分配超立方体索引for i=1:numel(GWO1)[GWO1(i).GridIndex,GWO1(i).GridSubIndex]=func_index(GWO1(i),G);end% 控制存档大小if numel(GWO1)>SmenEXTRA=numel(GWO1)-Smen;GWO1=func_Rep(GWO1,EXTRA,gamma);ycost=func_Costs(GWO1);G=func_Hypercubes(ycost,Ngd,alpha);end% 结果处理与绘图costs=func_Costs(GWO0);ycost=func_Costs(GWO1);figure(1)plot(costs(1,:),costs(2,:),'b.');hold onplot(ycost(1,:),ycost(2,:),'ro');legend('灰狼','Non-dominated解决方案');hold offdrawnowif it==1figure(2)plot(costs(1,:),costs(2,:),'b.');hold onplot(ycost(1,:),ycost(2,:),'ro');legend('灰狼','Non-dominated解决方案');title(['迭代次数:',num2str(it)]);endif it==50figure(3)plot(costs(1,:),costs(2,:),'b.');hold onplot(ycost(1,:),ycost(2,:),'ro');legend('灰狼','Non-dominated解决方案');title(['迭代次数:',num2str(it)]);endif it==200figure(4)plot(costs(1,:),costs(2,:),'b.');hold onplot(ycost(1,:),ycost(2,:),'ro');legend('灰狼','Non-dominated解决方案');title(['迭代次数:',num2str(it)]);endif it==500figure(5)plot(costs(1,:),costs(2,:),'b.');hold onplot(ycost(1,:),ycost(2,:),'ro');legend('灰狼','Non-dominated解决方案');title(['迭代次数:',num2str(it)]);end
end
644.本算法原理
灰狼优化(Grey Wolf Optimizer, GWO)是一种基于群体智能的全球优化算法,由Mirjalili等人在2014年提出,灵感来源于灰狼在自然界中的狩猎行为。该算法通过模拟灰狼的社会层级结构和狩猎策略,有效地搜索解空间,以找到问题的最优解。将GWO应用于多目标优化问题(Multi-Objective Optimization Problems, MOOPs),则形成了基于GWO的多目标优化算法,它能够处理具有多个冲突目标函数的优化问题,寻求所谓的帕累托最优解集。
4.1灰狼优化算法原理
在GWO中,算法中的每个搜索代理(解)被称作一只“狼”,它们在解空间中搜索以找到最优解。算法定义了三种角色的狼:α(领导者)、β(跟随者)和δ(猎手)。搜索过程通过模仿灰狼的领导模式、追捕猎物和群体协作行为进行。
算法步骤:
- 初始化:随机生成初始狼群,并计算每个狼的位置(解)的适应值。
- 更新α、β、δ:根据适应值确定当前群体中的领导者、跟随者和猎手。
- 更新位置:根据领导者的位置和其他狼的位置更新每只狼的位置。
- 评估并更新:计算新位置的适应值,并更新α、β、δ。
- 重复步骤2-4,直至满足停止准则(如迭代次数、适应值收敛)。
4.2 多目标优化问题(MOP)的帕累托最优解
在多目标优化中,帕累托最优解是指不存在另一个解在所有目标函数上都优于它,至少在一个目标上更好,其余目标至少一样好。寻找帕累托前沿(即所有非支配解的集合)是多目标优化的核心。
4.3 基于GWO的多目标优化算法
将GWO应用于多目标优化,关键在于如何在多目标环境下定义适应值和更新策略,以保证算法能够有效地探索和维护帕累托前沿。一种常用的方法是引入多目标适应度评价和多目标优化策略,如非支配排序和拥挤距离计算。

基于GWO的多目标优化算法通过模仿灰狼的社交行为和策略,结合多目标优化中的非支配排序和拥挤距离等策略,能够有效地搜索多目标优化问题的解空间,发现帕累托前沿解集。这种方法不仅保持了GWO的高效搜索能力,而且增加了处理多目标问题的能力,适用于解决工程、经济、环境等领域的复杂决策问题。
5.完整程序
VVV
相关文章:

基于GWO灰狼优化的多目标优化算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 4.1灰狼优化算法原理 4.2 多目标优化问题(MOP)的帕累托最优解 4.3 基于GWO的多目标优化算法 5.完整程序 1.程序功能描述 基于GWO灰狼优化的多目标优化算法matlab仿真,目标函数…...

排序算法-java版本
冒泡排序 原理:相邻的数据两两比较,小的放前面,大的放后面 int[] arr{3,5,2,1,4} for(int i0;i<arr.length-1;i){for(int j0;j<arr.length-1-i;j){if(arr[j]>arr[j1]){int temparr[j];arr[j]arr[j1];arr[j1]temp;}}}选择排序 升序…...

Java+前后端分离架构+ MySQL8.0.36产科信息管理系统 产科电子病历系统源码
Java前后端分离架构 MySQL8.0.36产科信息管理系统 产科电子病历系统源码 产科信息管理系统—住院管理 数字化产科住院管理是现代医院管理中的重要组成部分,它利用数字化技术优化住院流程,提升医疗服务质量和效率。以下是对数字化产科住院管理的详细阐述…...

js使用websocket,vue使用websocket,copy即用
新建一个文件 websocket.js // 定义websocket 地址 let socketurlDev "ws://192.000.0.0:8085/websocket/admin/"; //开发环境 let socketurlProd "wss://123456789.cn/prod-api/websocket/admin/"; //正式环境// 重连锁, 防止过多重连 let reconnectLo…...
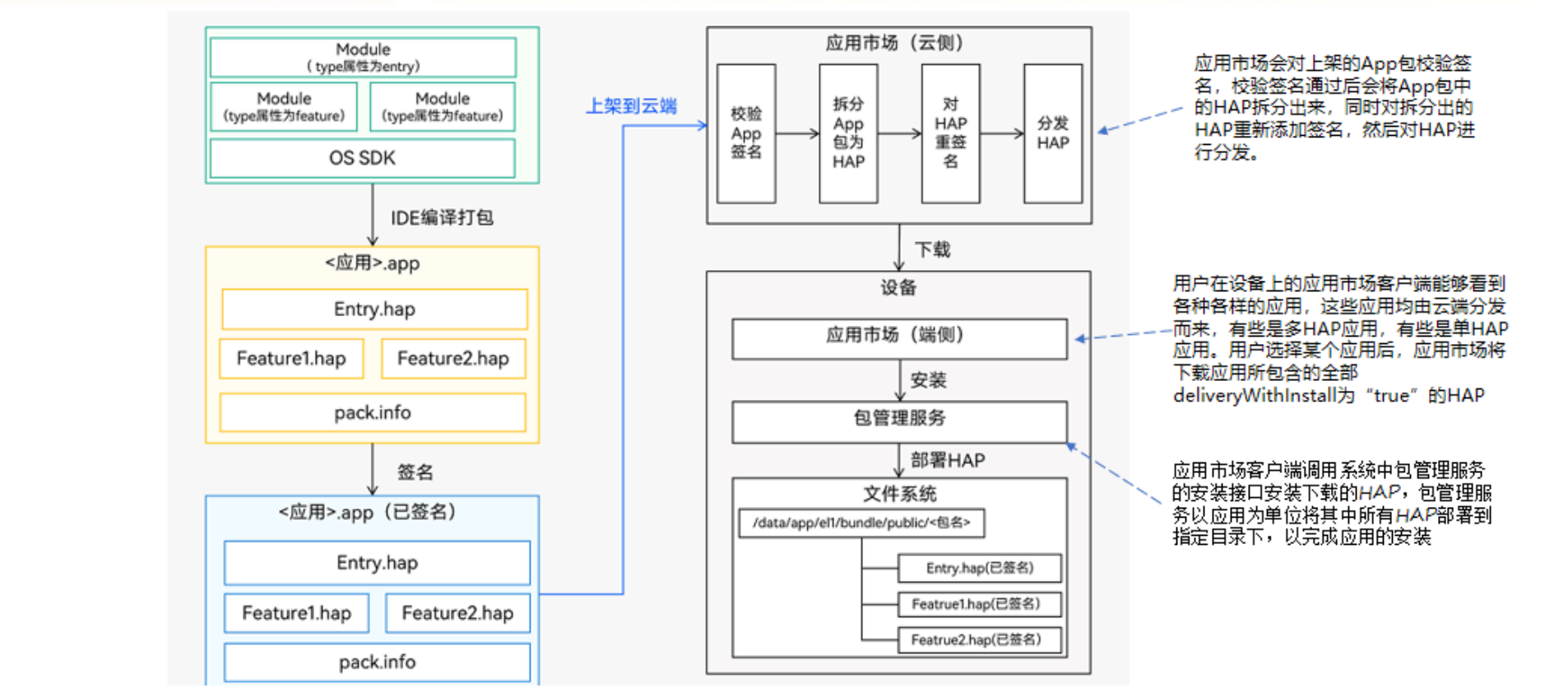
【鸿蒙学习笔记】Stage模型工程目录
官方文档:应用配置文件概述(Stage模型) 目录标题 FA模型和Stage模型工程级目录模块级目录app.json5module.json5程序执行流程程序基本结构开发调试与发布流程 FA模型和Stage模型 工程级目录 模块级目录 app.json5 官方文档:app.j…...

算法基础-----【动态规划】
动态规划(待完善) 动规五部曲分别为: 确定dp数组(dp table)以及下标的含义确定递推公式(状态转移公式)dp数组如何初始化确定遍历顺序举例推导dp数组、 动态规划的核心就是递归剪枝(存储键值,…...

Java中的响应式编程与Reactor框架
Java中的响应式编程与Reactor框架 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 响应式编程(Reactive Programming)是一种面向数据流…...
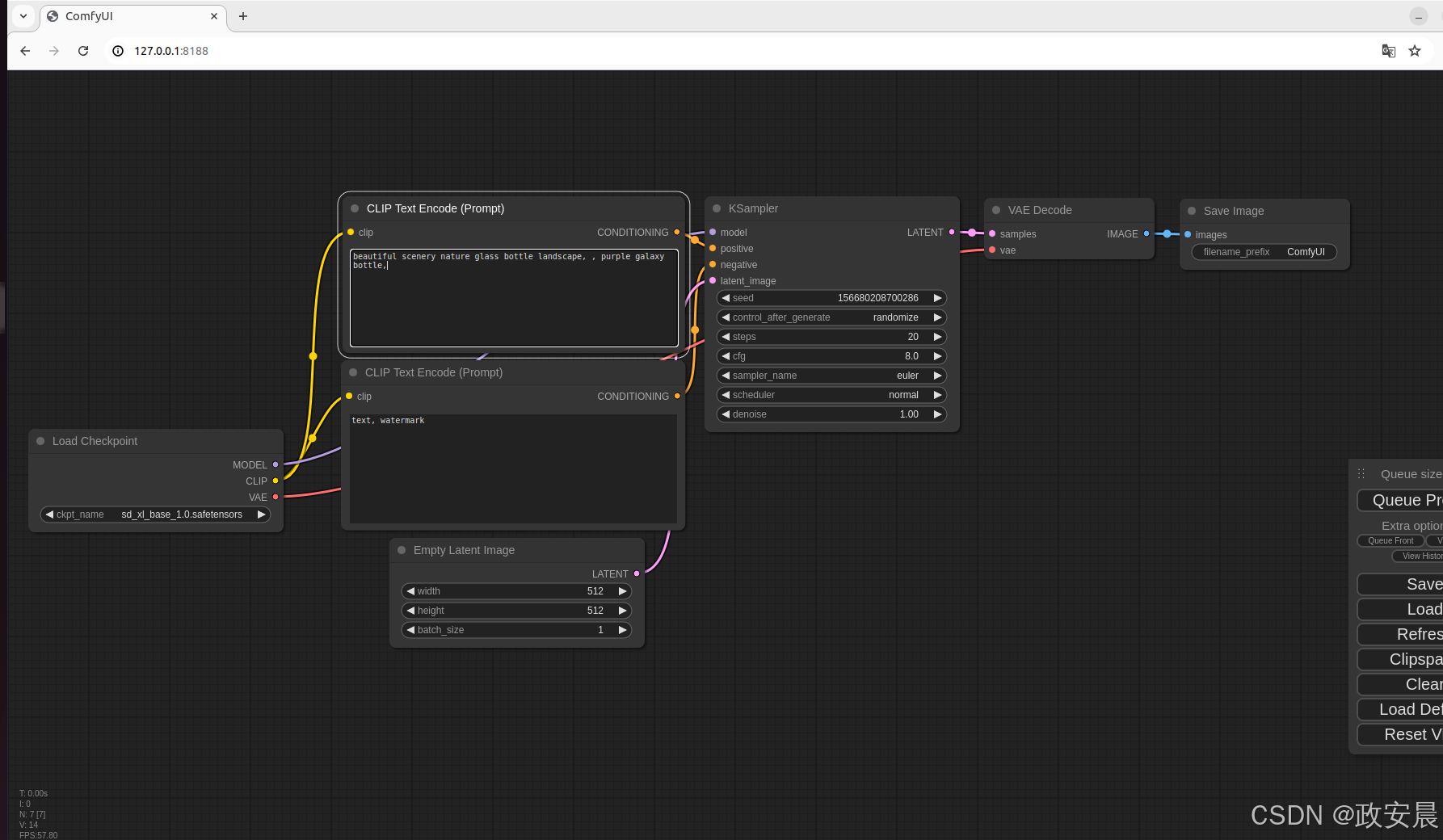
政安晨【零基础玩转各类开源AI项目】基于Ubuntu系统部署ComfyUI:功能最强大、模块化程度最高的Stable Diffusion图形用户界面和后台
目录 ComfyUI的特性介绍 开始安装 做点准备工作 在Conda虚拟环境中进行 依赖项的安装 运行 政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 零基础玩转各类开源AI项目 希望政安晨的博客能够对您有所裨益,如有不足之处&…...

匿名内部类
下面代码中,Person24 是一个抽象类,这意味着它不能被直接实例化,只能通过继承它的子类来实现其抽象方法。代码片段中展示了如何使用匿名内部类来实现一个抽象类的实例。 package chapter04;public class Java24_Object_匿名内部类 {public s…...

react_web自定义组件_多类型Modal_搜索栏Search
目录 一、带输入框的Modal 二、提示框Modal 三、搜索栏Search 在做项目时引入一些现成的UI组件,但是如果和设计图冲突太大,更改时很麻烦,如果自己写一个通用组件其实也就几十分钟或者几个小时,而且更具UI设计更改也比较好更改&…...

Apache Flink架构介绍
目录 一、Apache Flink架构组件栈 1.1 概述 1.2 架构图 1.3 架构分层组件说明 1.3.1 物理部署层 1.3.2 Runtime 核心层 1.3.3 API & Libraries层 二、Flink运行时架构 2.1 概述 2.2 架构图 2.3 架构角色和组件 2.3.1 Flink Clients客户端 2.3.2 JobManager 2.…...

华为HCIP Datacom H12-821 卷28
1.单选题 下面是一台路由器的部分配置,关于该部分配置描述正确的是,[HUAWEI]ip ip-prefx pl permit 10.0.192.0 8greater-equal17 less-equal 18 A、10.0.192.0/8网段内,掩码长度为18的路由会匹配到该前缀列表,匹配规则为允许 B、10.0.192.0/8网段内掩码长度为21的路…...

安装Nginx以及简单使用 —— windows系统
一、背景 Nginx是一个很强大的高性能Web和反向代理服务,也是一种轻量级的Web服务器,可以作为独立的服务器部署网站,应用非常广泛,特别是现在前后端分离的情况下。而在开发过程中,我们常常需要在window系统下使用Nginx作…...

【UE5.3】笔记8 添加碰撞,检测碰撞
添加碰撞 打开BP_Food,添加Box Collision组件,与unity类似: 调整Box Collision的大小到刚好包裹物体,通过调整缩放和盒体范围来控制大小,一般先调整缩放找个大概大小,然后调整盒体范围进行微调。 碰撞检测 添加好碰撞…...

丝滑流畅!使用kimi快速完成论文仿写
学境思源,一键生成论文初稿: AcademicIdeas - 学境思源AI论文写作 今天的分享,我们将带大家探索一种新的学术写作技巧——使用Kimi进行论文仿写。本文将深入解析如何利用Kimi的智能辅助功能,提高论文写作的效率和质量,…...

【C++】认识使用string类
【C】STL中的string类 C语言中的字符串标准库中的string类string类成员变量string类的常用接口说明成员函数string(constructor构造函数)~string(destructor析构函数)默认赋值运算符重载函数 遍历string下标[ ]迭代器范围for反向迭代器 capacitysizelengthmax_sizeresizecapaci…...

如何在 Odoo 16 中对 Many2Many 字段使用 Group by
Many2many 字段与 Many2one 字段类似,因为它们在模型之间建立了新的关系。在Odoo 16中,您无法按 many2many 字段分组,因为可以使用 many2many 记录选择任何记录。当您使用 many2many 字段给出 group by 过滤器时,您将遇到断言错误。 介绍如何在 Odoo 16 中使用 Many2Many…...

PCL从理解到应用【03】KDTree 原理分析 | 案例分析 | 代码实现
前言 本文分析KDTree的原理,集合案例深入理解,同时提供源代码。 三个案例:K近邻搜索、半径内近邻搜索、近似最近邻搜索。方法对比,如下表所示: 特性K近邻搜索半径内近邻搜索近似最近邻搜索描述查找K个最近邻点查找指…...
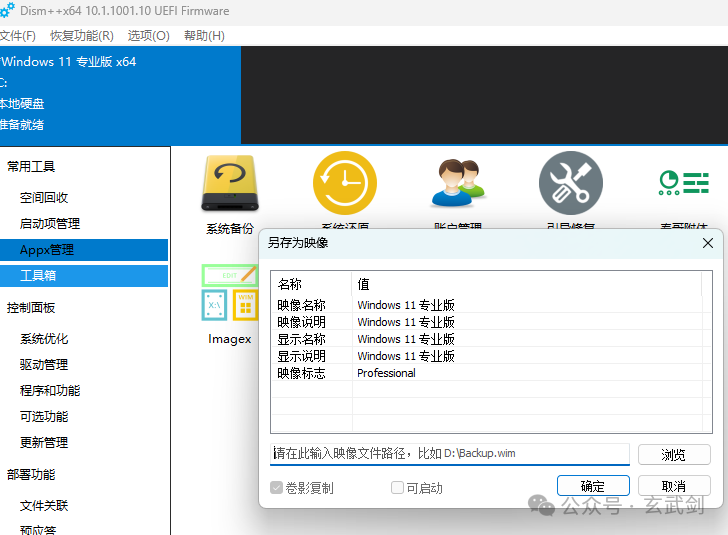
Windows 11内置一键系统备份与还原 轻松替代Ghost
面对系统崩溃、恶意软件侵袭或其他不可预见因素导致的启动失败,Windows 7~Windows 11内置的系统映像功能能够迅速将您的系统恢复至健康状态,确保工作的连续性和数据的完整性。 Windows内置3种备份策略 U盘备份:便携且安全 打开“创建一个恢…...

leetCode-hot100-动态规划专题
动态规划 动态规划定义动态规划的核心思想动态规划的基本特征动态规划的基本思路例题322.零钱兑换53.最大子数组和72.编辑距离139.单词拆分62.不同路径63.不同路径Ⅱ64.最小路径和70.爬楼梯121.买卖股票的最佳时机152.乘积最大子数组 动态规划定义 动态规划(Dynami…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
