数据结构 —— 最小生成树
数据结构 —— 最小生成树
- 什么是最小生成树
- Kruskal算法
- Prim算法
今天我们来看一下最小生成树:
我们之前学习的遍历算法并没有考虑权值,仅仅就是遍历结点:
 今天的最小生成树要满足几个条件:
今天的最小生成树要满足几个条件:
- 考虑权值
- 所有结点联通
- 权值之和最小
- 无环

什么是最小生成树
最小生成树(Minimum Spanning Tree,简称MST)是指在一个加权的、无向的连通图中,由所有顶点构成的一个子图,这个子图是一棵树,并且其所有边的权重之和最小。换句话说,最小生成树是在保证图中所有顶点连通的前提下,使得连接这些顶点的边的总成本最低的一棵树。
最小生成树具有以下特性:
- 它包含图中的所有顶点。
- 它是一个没有环的连通子图(即树)。
- 它的边数比顶点数少一(对于 n 个顶点的图,有 n-1 条边)。
- 它的边的总权重是所有可能生成树中最小的。
最小生成树在很多实际应用中都有重要作用,例如在设计电信网络时,为了连接多个地点而需要铺设电缆或光纤,最小生成树可以用来确定一种成本最低的铺设方案。
求解最小生成树的常用算法包括:
- Kruskal算法:此算法通过不断选择权重最小的边来构建最小生成树,同时避免添加会导致环路形成的边。它通常利用并查集(Disjoint Set Union)数据结构来检测环路。
- Prim算法:此算法从任意一个顶点开始,逐步将顶点及其权重最小的连接边加入到生成树中,直到所有顶点都被包含进来。Prim算法可以使用优先队列(Priority Queue)来高效地选择下一个应加入的边。
我们今天就来介绍一下这两种算法:
Kruskal算法
Kruskal算法,简单来说,就是把所有边拿出来,从小到大挑边,构成最小生成树:
Kruskal算法是一种用于寻找加权、无向连通图的最小生成树(Minimum Spanning Tree, MST)的贪心算法。它的核心思想是在不形成任何环路的情况下,选择权重最小的边来构建生成树,直到所有的顶点都被包含在树中。
以下是Kruskal算法的主要步骤:
- 排序边:将图中所有的边按照权重从小到大排序。
- 初始化森林:创建一个森林,其中每个顶点都是一个单独的树(即每个顶点都是一个独立的连通分量)。
- 选择边:遍历排序后的边列表。对于每条边,检查它的两个端点是否已经在同一棵树中(即是否属于同一个连通分量)。如果不是,将这条边添加到最小生成树中,并将这两个顶点所在的树合并成一棵更大的树。
- 重复步骤3:继续选择满足条件的边,直到最小生成树中包含了图中的所有顶点,或者已经选择了
n-1条边(其中n是顶点的数量)。

Kruskal算法的关键在于能够快速地检测边的两个端点是否属于同一棵树,这通常是通过使用并查集(Union-Find)数据结构来实现的。并查集允许我们在对数时间内执行“查找”操作(确定顶点所属的树)和“合并”操作(将两棵树合并成一棵树)。
// 使用Kruskal算法计算最小生成树的总权重
W Kruskal(Self& minTree) // Self应为当前类的引用,minTree是用于存储最小生成树的实例
{// 初始化最小生成树的顶点集和索引minTree._vertex = _vertex;minTree._index = _index;minTree._matrix.resize(_vertex.size()); // 创建一个邻接矩阵,用于存储最小生成树中的边的权重for (auto& e : minTree._matrix) // 将邻接矩阵的所有元素初始化为最大权重值MAX_W{e.resize(_vertex.size(), MAX_W);}// 创建一个优先级队列,用于存储边的信息priority_queue<Edge, vector<Edge>, greater<Edge>> pq;// 将所有边(除了自环和重复边)加入优先级队列for (size_t i = 0; i < _vertex.size(); i++) {for (size_t j = 0; j < _vertex.size(); j++) {if (i < j && _matrix[i][j] != MAX_W) // 确保不加入自环和重复边{pq.push(Edge(i, j, _matrix[i][j])); // 将边加入优先级队列}}}// 初始化变量,用于记录最小生成树的总权重和边的数量W total = W();int size = 0;UnionFindSet ufs(_vertex.size()); // 创建并查集,用于判断顶点是否已经连接while (!pq.empty()) // 当优先级队列非空时{Edge min = pq.top(); // 取出权重最小的边pq.pop(); // 移除已取出的边// 判断边的两个顶点是否已经在同一集合内(即是否已经连接)if (!ufs.InSet(min._srci, min._desi)) {cout << _vertex[min._srci] << "-" << _vertex[min._desi] << ":" << _matrix[min._srci][min._desi] << endl; // 打印边的信息minTree._AddEdge(min._srci, min._desi, min._w); // 将边加入最小生成树total += min._w; // 更新最小生成树的总权重ufs.Union(min._srci, min._desi); // 合并两个顶点所在的集合++size; // 增加边的数量}}cout << endl;minTree.Print(); // 打印最小生成树// 如果边的数量等于顶点数量减一,则返回最小生成树的总权重if (size == _vertex.size() - 1){return total;}else{return W(); // 否则返回默认权重值(可能表示无法形成最小生成树)}
}
我们可以来测试一下:
void TestGraph2(){string a[] = {"海皇","高斯","小傲","小潮","胖迪","小杨","皖皖"};Graph<string, int,INT_MAX, false> g1(a, sizeof(a)/sizeof(a[0]));g1.AddEdge("小潮", "小傲", 30);g1.AddEdge("小潮", "高斯", 83);g1.AddEdge("小潮", "海皇", 34);g1.AddEdge("胖迪", "海皇", 78);g1.AddEdge("胖迪", "小傲", 76);g1.AddEdge("小杨", "皖皖", 54);g1.AddEdge("小杨", "高斯", 48);g1.Print();cout << endl;Graph<string, int, INT_MAX, false> kminTree;cout << "Kruskal:" << g1.Kruskal(kminTree) << endl;}
 按照Kruskal算法,构建出来的图是这样的:
按照Kruskal算法,构建出来的图是这样的:
 胖迪和海皇的关系被抹除了,其实我们之前的图里有环:
胖迪和海皇的关系被抹除了,其实我们之前的图里有环:

Kruskal算法的时间复杂度主要取决于排序边的操作和并查集的效率。在最好的情况下,排序边的时间复杂度为O(E log E),其中E是边的数量;并查集操作的时间复杂度接近常数,因此整个算法的时间复杂度近似为O(E log E)。由于排序的主导作用,该算法适用于边的数量远小于顶点数量平方的图,即稀疏图。
Prim算法
Prim算法和上面的思想差不多,但是,Prim算法会从一个顶点开始,这里我假设是从"小潮"开始:

跟小潮连接的3条边,会进入优先级队列,维护起来:
 接下来,会选择30的权重来构造,然后30这条边的另一边的小傲的边入优先级队列:
接下来,会选择30的权重来构造,然后30这条边的另一边的小傲的边入优先级队列:

以此类推:
// 使用Prim算法构建并返回最小生成树的总权重
W Prim(Self& minTree, const V& vertex) // Self应该是当前类的引用,minTree是用于存储最小生成树的实例,vertex是顶点的容器
{// 初始化最小生成树的顶点集和索引minTree._vertex = _vertex;minTree._index = _index;minTree._matrix.resize(_vertex.size()); // 创建一个邻接矩阵,用于存储最小生成树中的边的权重// 初始化邻接矩阵的所有元素为最大权重值MAX_Wfor (auto& e : minTree._matrix){e.resize(_vertex.size(), MAX_W);}// 区分顶点集合:已选择和未选择size_t srcIndex = FindSrci(vertex); // 找到起始顶点的索引vector<bool> select(_vertex.size(), false); // 已选择顶点集合,初始时所有顶点都未选择vector<bool> non_select(_vertex.size(), true); // 未选择顶点集合,初始时所有顶点都未被选择select[srcIndex] = true; // 起始顶点被标记为已选择non_select[srcIndex] = false; // 起始顶点从未选择集合中移除// 创建一个优先级队列,用于存储待处理的边priority_queue<Edge, vector<Edge>, greater<Edge>> pq; // 边按权重从小到大排序// 将起始顶点的邻接边加入优先级队列for (int i = 0; i < _vertex.size(); i++){if (_matrix[srcIndex][i] != MAX_W) // 如果存在边,且不是最大权重(表示边存在){pq.push(Edge(srcIndex, i, _matrix[srcIndex][i])); // 加入边信息到优先级队列}}// 初始化计数器和总权重size_t size = 0;W total = W(); // 初始化总权重为0// 当优先级队列非空时while (!pq.empty()){Edge min = pq.top(); // 获取当前权重最小的边pq.pop(); // 从队列中移除已处理的边// 如果目标顶点已被选择,跳过这条边if (select[min._desi]) continue;// 输出边的信息cout << _vertex[min._srci] << "-" << _vertex[min._desi] << ":" << _matrix[min._srci][min._desi] << endl;// 添加边到最小生成树minTree._AddEdge(min._srci, min._desi, min._w);// 标记目标顶点为已选择select[min._desi] = true;non_select[min._desi] = false;++size; // 已处理的边数量加1total += min._w; // 更新总权重// 将新加入顶点的邻接边加入优先级队列for (size_t i = 0; i < _vertex.size(); i++){if (_matrix[min._desi][i] != MAX_W && non_select[i]) // 如果存在边且目标顶点未被选择{pq.push(Edge(min._desi, i, _matrix[min._desi][i])); // 加入边信息到优先级队列}}}// 打印最小生成树minTree.Print();// 如果边的数量等于顶点数量减一,则返回最小生成树的总权重if (size == _vertex.size() - 1){return total;}else{return W(); // 否则返回默认权重值(可能表示无法形成最小生成树)}
}
void TestGraph2(){string a[] = {"海皇","高斯","小傲","小潮","胖迪","小杨","皖皖"};Graph<string, int,INT_MAX, false> g1(a, sizeof(a)/sizeof(a[0]));g1.AddEdge("小潮", "小傲", 30);g1.AddEdge("小潮", "高斯", 83);g1.AddEdge("小潮", "海皇", 34);g1.AddEdge("胖迪", "海皇", 78);g1.AddEdge("胖迪", "小傲", 76);g1.AddEdge("小杨", "皖皖", 54);g1.AddEdge("小杨", "高斯", 48);g1.Print();cout << endl;Graph<string, int, INT_MAX, false> kminTree;cout << "Kruskal:" << g1.Kruskal(kminTree) << endl;cout << endl;Graph<string, int, INT_MAX, false> pminTree;cout << "Prim:" << g1.Prim(pminTree,"小潮") << endl;}

Prim算法同样是用于寻找加权无向图的最小生成树(Minimum Spanning Tree, MST)的一种贪心算法。与Kruskal算法不同的是,Prim算法从一个顶点开始,逐步添加最短的边来扩展树,直到包含所有的顶点。
Prim算法基本步骤:
- 选择任意一个顶点作为起始顶点。
- 在当前树的顶点的邻接边中找到权重最小的边,将这条边添加到树中,并将新的顶点也添加进来。
- 重复步骤2,直到树包含所有的顶点。
这是两种算法挑选边的过程和最后结果,大家可以类比对比:
//Kruskal算法W Kruskal(Self& minTree){//初始化minTree._vertex = _vertex;minTree._index = _index;minTree._matrix.resize(_vertex.size());for (auto& e : minTree._matrix){e.resize(_vertex.size(), MAX_W);}//优先级队列priority_queue<Edge, vector<Edge>, greater<Edge>> pq;for (size_t i = 0; i < _vertex.size(); i++){for (size_t j = 0; j < _vertex.size(); j++){if (i < j && _matrix[i][j] != MAX_W){pq.push(Edge(i, j, _matrix[i][j]));}}}//拿边构造最小生成树W totoal = W();int size = 0;UnionFindSet ufs(_vertex.size());while (!pq.empty()){Edge min = pq.top();//出边pq.pop();//判断是否在同一集合if (!ufs.InSet(min._srci ,min._desi)){cout << _vertex[min._srci] << "-" << _vertex[min._desi] <<":" << _matrix[min._srci][min._desi] << endl;minTree._AddEdge(min._srci, min._desi, min._w);totoal += min._w;//合并ufs.Union(min._srci, min._desi);++size;}}cout << endl;minTree.Print();if (size == _vertex.size() - 1){return totoal;}else{return W();}}W Prim(Self& minTree,const V& vertex){//初始化minTree._vertex = _vertex;minTree._index = _index;minTree._matrix.resize(_vertex.size());for (auto& e : minTree._matrix){e.resize(_vertex.size(), MAX_W);}//区分集合size_t srcIndex = FindSrci(vertex);vector<bool> select(_vertex.size(), false);vector<bool> non_select(_vertex.size(), true);select[srcIndex] = true;non_select[srcIndex] = false;//开始入边priority_queue<Edge, vector<Edge>, greater<Edge>> pq;for (int i = 0; i < _vertex.size(); i++){if (_matrix[srcIndex][i] != MAX_W){pq.push(Edge(srcIndex, i, _matrix[srcIndex][i]));}}size_t size = 0;W totoal = W();while (!pq.empty()){Edge min = pq.top();pq.pop();if (select[min._desi])continue;cout << _vertex[min._srci] << "-" << _vertex[min._desi] <<":" << _matrix[min._srci][min._desi] << endl;minTree._AddEdge(min._srci, min._desi, min._w);select[min._desi] = true;non_select[min._desi] = false;++size;totoal += min._w;//新入的顶点的边也加入到优先级队列for (size_t i = 0; i < _vertex.size(); i++){if (_matrix[min._desi][i] != MAX_W && non_select[i]){pq.push(Edge(min._desi, i, _matrix[min._desi][i]));}}}minTree.Print();if (size == _vertex.size() - 1){return totoal;}else{return W();}}

相关文章:

数据结构 —— 最小生成树
数据结构 —— 最小生成树 什么是最小生成树Kruskal算法Prim算法 今天我们来看一下最小生成树: 我们之前学习的遍历算法并没有考虑权值,仅仅就是遍历结点: 今天的最小生成树要满足几个条件: 考虑权值所有结点联通权值之和最小无环…...

初学Spring之 JavaConfig 实现配置
使用 Java 方式配置 Spring 写个实体类: Component 表示这个类被 Spring 接管了,注册到了容器中 package com.demo.pojo;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component;Component //…...

在Java项目中实现实时日志分析
在Java项目中实现实时日志分析 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 随着互联网应用的发展,实时日志分析成为了保证系统稳定性、性能优化…...

Git基础知识与常用命令指南
这是一个Git基础知识和常用命令的简要指南,涵盖了日常开发中最常用的操作。你可以将这个指南保存下来,作为日常工作的参考。 目录 基础篇1. Git基本概念2. 配置Git3. 创建仓库4. 基本的工作流程5. 分支操作6. 查看历史7. 撤销更改8. 远程仓库操作 Git进阶知识与技巧指南1. 分…...

第8章:Electron 剪贴版和消息通知
在本章中,我们将介绍如何在Electron应用中与操作系统进行集成。这些操作包括剪贴板操作、通知系统、原生对话框等功能。 8.1 剪贴板操作 Electron 提供了 clipboard 模块,允许我们在应用中访问和操作剪贴板内容。以下是一些基本的剪贴板操作示例。 8.…...
Android zygote访谈录
戳蓝字“牛晓伟”关注我哦! 用心坚持输出易读、有趣、有深度、高质量、体系化的技术文章,技术文章也可以有温度。 本文摘要 本文以访谈的方式来带大家了解zygote进程,了解zygote进程是啥?它的作用是啥?它是如何一步…...

nuxt、vue树形图d3.js
直接上代码 //安装 npm i d3 --save<template><div class"d3"><div :id"id" class"d3-content"></div></div> </template> <script> import * as d3 from "d3";export default {props: {d…...

香橙派AIpro测评:yolo8+usb鱼眼摄像头的Camera图像获取及识别
一、前言 近期收到了一块受到业界人士关注的开发板"香橙派AIpro",因为这块板子具有极高的性价比,同时还可以兼容ubuntu、安卓等多种操作系统,今天博主便要在一块832g的香橙派AI香橙派AIpro进行YoloV8s算法的部署并使用一个外接的鱼眼USB摄像头…...
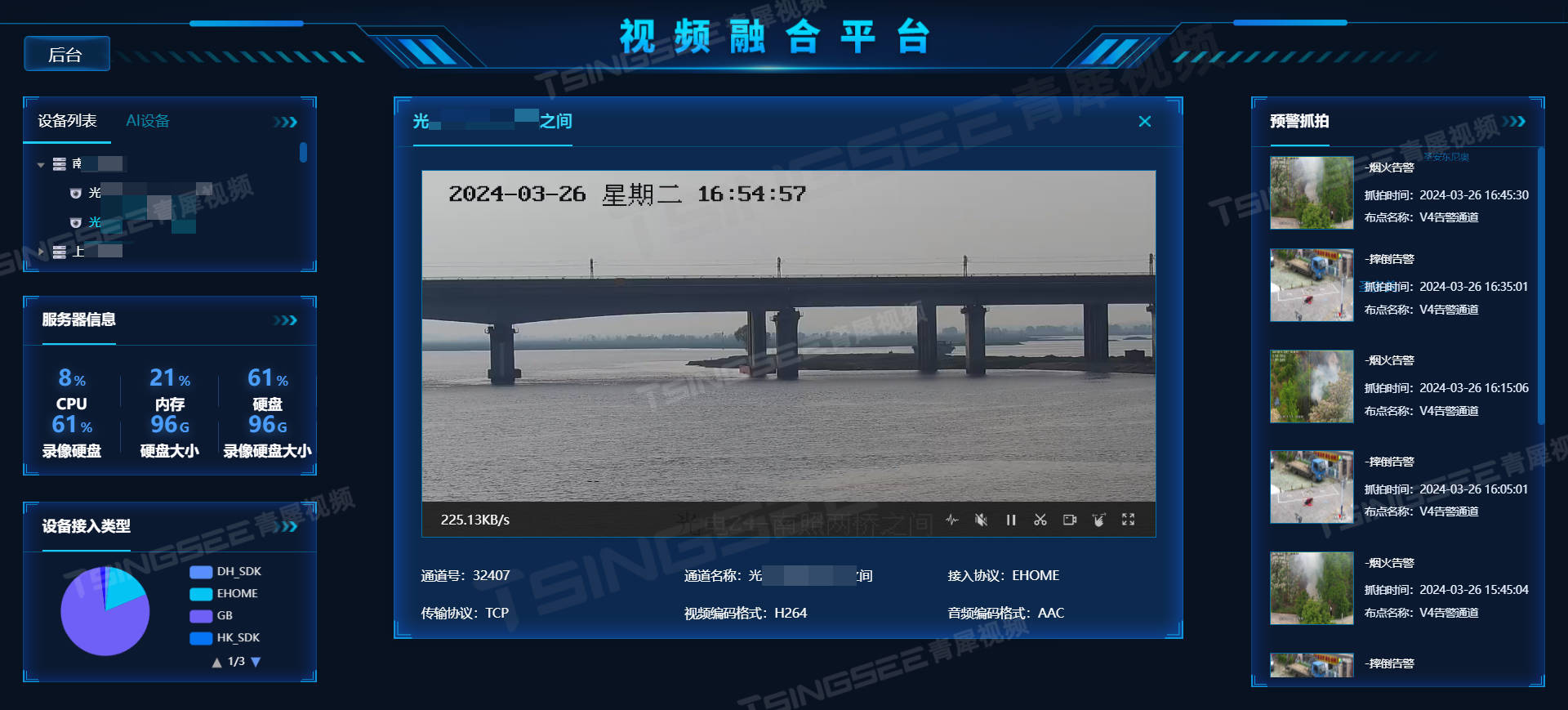
大华设备接入GB28181视频汇聚管理平台EasyCVR安防监控系统的具体操作步骤
智慧城市/视频汇聚/安防监控平台EasyCVR兼容性强,支持多协议接入,包括国标GB/T 28181协议、GA/T 1400协议、部标JT808协议、RTMP、RTSP/Onvif协议、海康Ehome、海康SDK、大华SDK、华为SDK、宇视SDK、乐橙SDK、萤石云SDK等,并能对外分发RTMP、…...

Laravel包开发指南:构建可重用组件的艺术
标题:Laravel包开发指南:构建可重用组件的艺术 Laravel不仅是一个强大的Web应用框架,它的包(Package)系统也为开发者提供了构建和共享可重用组件的能力。通过包开发,开发者可以轻松地扩展Laravel的功能&am…...

JavaDS预备知识
集合框架 Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 interfaces和其实现类 classes 。 其主要表现为将多个元素 element 置于一个单元中,对数据进行创建(Create)、读取(Retrieve…...

日常学习--20240705
1、IO流 按照IO操作的数据类型分为字节流和字符流: 字节流:又分为输入流(其他程序传递过来的数据,读取流中的数据)和输出流(往流中写数据,传递给其他程序);可以操作二进制文件&…...

Java中初始化一个List的多种方式
1.最原始的方式:先创建,然后再添加元素 List<String> list new ArrayList<>(); list.add("apple"); list.add("banana"); list.add("cherry");2.使用Arrays.asList 这是一种快速方便的方式,直接…...
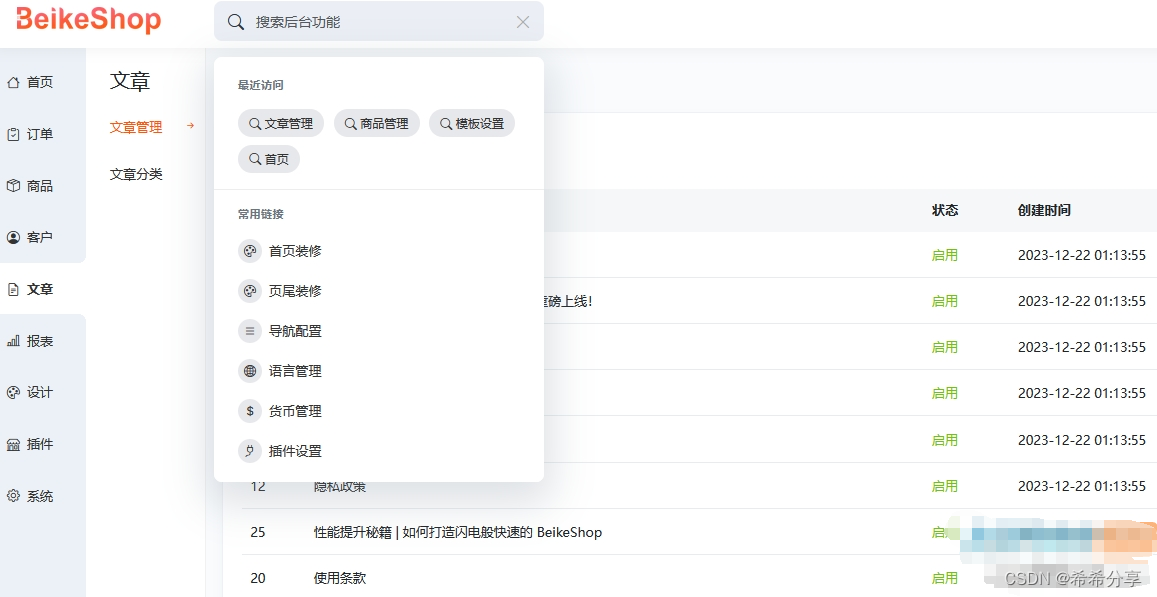
BeikeShop多国语言多货币商城系统源码基于Laravel框架
BeikeShop是基于 Laravel 开发的一款开源商城系统,支持多语言商城 多货币商城 100%全开源 ChatGPT OpenAI B2C商城系统 H5商城 PHP商城系统 商城源码 PC商城 跨境电商系统 跨境商城系统 电商商城系统 Laravel 10 框架开发系统,支持插件市场。 Event 机制…...

gradle构建工具
setting.gradle // settings.gradle rootProject.name my-project // 指定根项目名称include subproject1, subproject2 // 指定子项目名称,可选jar包名称 方式一 jar {archiveBaseName my-application // 设置 JAR 文件的基本名称archiveVersion 1.0 // 设置…...

Java需要英语基础吗?
Java编程语言本身并不要求必须有很强的英语基础,因为Java的语法和逻辑是独立于任何特定语言的。我收集归类了一份嵌入式学习包,对于新手而言简直不要太棒,里面包括了新手各个时期的学习方向编程教学、问题视频讲解、毕设800套和语言类教学&am…...

14-36 剑和诗人10 - 用LLM构建 AI 代理平台
介绍 在当今快速发展的技术环境中,大型语言模型 (LLM) 和 AI 代理正在改变我们与信息交互、实现流程自动化以及应对不同行业复杂挑战的方式。随着这些强大的模型不断发展,对能够无缝集成和协调它们的强大平台的需求变得越来越重要。 让我们深入研究设计…...

如何在Java中实现批量数据处理
如何在Java中实现批量数据处理 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. 引言 在大数据时代,处理大量数据是许多应用程序中必不可少的需…...
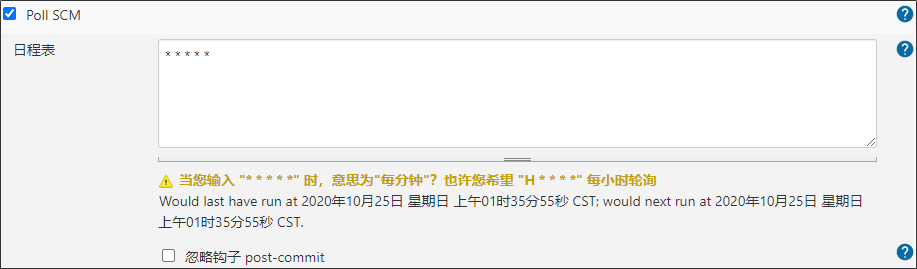
项目部署_持续集成_Jenkins
1 今日内容介绍 1.1 什么是持续集成 持续集成( Continuous integration , 简称 CI )指的是,频繁地(一天多次)将代码集成到主干 持续集成的组成要素 一个自动构建过程, 从检出代码、 编译构建…...

如何选择TikTok菲律宾直播网络?
为了满足用户对于实时互动的需求,TikTok推出了直播功能,让用户能够与粉丝即时交流。本文将探讨如何选择适合的TikTok菲律宾直播网络,并分析OgLive是否是值得信赖的选择。 TikTok菲律宾直播网络面临的挑战 作为全球领先的短视频平台ÿ…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
