【算法】(C语言):快速排序(递归)、归并排序(递归)、希尔排序
快速排序(递归)
- 左指针指向第一个数据,右指针指向最后一个数据。取第一个数据作为中间值。
- 右指针指向的数据 循环与中间值比对,若大于中间值,右指针往左移动一位,若小于中间值,右指针停住。右指针指向的数据放入左指针指向的位置。
- 左指针指向的数据 循环与中间值比对,若小于中间值,左指针往右移动一位,若大于中间值,左指针停住。左指针指向的数据放入右指针指向的位置。
- 重复2和3,直到左指针和右指针指向同一个位置pos,则中间值放入该位置pos。
- 从中间值所在位置pos将数据分成左边和右边两部分。左边数值都比中间值小,右边数值都比中间值大。
- 重复1-5,直到左边或右边只有一个数据。到此排序完成。
(注:左指针指向的数据始终比中间值小,右指针指向的数据始终比中间值大。)
时间复杂度:最好情况 O(nlogn),最坏情况 O(),平均情况 O(nlogn)
- 左右指针依次从头或从尾与中间值比对,一轮比对约n次。
- 若每次取的中间值正好是中间位置的数据,每次都是对半拆分,拆分层级logn,则所有数据需约logn轮的比对,总时间 约 O(nlogn)。
- 若已经排好序了,则每次取的中间值都是最小或最大值,则每次都是依次从下一位数据重新开始,类似斜树,最坏时间约 O(
)。
空间复杂度:最好情况 O(logn),最坏情况 O(n)。
- 在原位置排序,使用栈作为辅助空间。每次递归,中间值入栈,递归结束,中间值出栈。
- 若最好情况,拆分层级logn,最多logn个中间值在栈中,则即空间使用 O(logn)。
- 若最坏情况,则递归n次,即空间使用约 O(n)。
C语言实现:(quicksort.c)
#include <stdio.h>/* function prototype */
void quicksort(int *, int, int); // quick sort (recursion)
void traverse(int *, int); // show element one by one/* main function */
int main(void)
{int arr[] = {4,2,6,9,5,1,3};int n = sizeof(arr) / sizeof(int);traverse(arr, n);quicksort(arr, 0, n - 1);printf("[ after quick sort ] ");traverse(arr, n);return 0;
}
/* subfunction */
void quicksort(int *array, int start, int end) // quick sort (recursion)
{if(start >= end) return ;int low = start, high = end;int middata = array[low]; // the first element as middle datawhile(low < high){// right side, data is bigger than middle data.High index move a step to left while(low < high && array[high] >= middata) high--;// right side, if data is smaller than middle data, data change to low index array[low] = array[high];// left side, data is smaller than middle data.Low index move a step to rightwhile(low < high && array[low] < middata) low++;// left side, if data is bigger than middle data, data change to high indexarray[high] = array[low];}// the middle data in the correct positionarray[low] = middata;// from the position of the middle data, split to two sidesquicksort(array, start, low - 1);quicksort(array, low + 1, end);
}void traverse(int *array, int length) // show element one by one
{printf("elements(%d): ", length);for(int k = 0; k < length; k++){printf("%d ", array[k]);}printf("\n");
}编译链接: gcc -o quicksort quicksort.c
执行可执行文件: ./quicksort
![]()
归并排序(递归)
- 从中间位置,将数据拆分成左右两部分。再分别将左右两部分从各自中间位置再拆分成左右两部分。直到左边或右边只有一个元素。
- 将最多只有一个元素的左右两边,排序合并在一起。
- 将排好序的左右两边,排序合并在一起。
- 重复3,直到全部排好序。
时间复杂度:最好情况 O(nlogn),最坏情况 O(nlogn),平均情况 O(nlogn)
- 每次对半拆分,拆分层级logn,所有数据都需要比对 进行重新排序合并,一轮比对合并约n次,共约logn轮,则总时间约 nlogn,即 O(nlogn)。
空间复杂度:O(n)
- 有多少数据,就需要多少额外的空间存储 已排好序的数据,即 O(n)。
C语言实现:(mergesort.c)
#include <stdio.h>
#include <math.h>/* function prototype */
void mergesort(int *, int, int); // merge sort (recursion)
void traverse(int *, int); // show element one by one/* main function */
int main(void)
{int arr[] = {4,2,6,9,5,1,3};int n = sizeof(arr) / sizeof(int);traverse(arr, n);mergesort(arr, 0, n - 1);printf("[ after merge sort ] ");traverse(arr, n);return 0;
}
/* subfunction */
void mergesort(int *array, int start, int end) // merge sort (recursion)
{if(start >= end) return ;// from the middle, split the array to the left side and the right sideint mid = start + ceil((end - start) / 2);mergesort(array, start, mid);mergesort(array, mid + 1, end);// merge the left and right, sort to the new arrayint tmparr[end - start + 1];int i = start, j = mid + 1;for(int k = 0; k <= end - start; k++){// the right side is over or left data < right data, copy the left dataif(j > end || (i <= mid && array[i] < array[j])){tmparr[k] = array[i];i++;}// the left side is over or left data >= right data, copy the right dataelse{tmparr[k] = array[j];j++;}}// elements in the new array copy to the original arrayfor(int i = start, k = 0; i <= end; i++, k++){array[i] = tmparr[k];}
}void traverse(int *array, int length) // show element one by one
{printf("elements(%d): ", length);for(int k = 0; k < length; k++){printf("%d ", array[k]);}printf("\n");
}编译链接: gcc -o mergesort mergesort.c
执行可执行文件: ./mergesort
希尔排序
- 取一定间隔(开始一般为数据量的一半),将数据分为多个组,每个组分别排序。
- 将间隔减半,数据分为多个组,每个组分别排序。
- 重复2,直到间隔为1,完成最后的排序。
时间复杂度:O() - O(
)
- 插入排序的升级。先根据大间隔,按组进行插入排序,再依次减小间隔,按组进行插入排序。
- 比
快,但比nlogn慢。
空间复杂度:O(1)
- 在原位置排序,只重复使用了用于交换的临时空间,不随数据量的变动而变动,空间使用为常量(1)。
C语言实现:(shellsort.c)
#include <stdio.h>
#include <math.h>/* function prototype */
void shellsort(int *, int); // shell sort
void traverse(int *, int); // show element one by one/* main function */
int main(void)
{int arr[] = {4,2,6,9,5,1,3};int n = sizeof(arr) / sizeof(int);traverse(arr, n);shellsort(arr, n);printf("[ after shell sort ] ");traverse(arr, n);return 0;
}
/* subfunction */
void shellsort(int *array, int length) // shell sort
{int gap = ceil(length / 2); // steps of two comparative datawhile(gap > 0){// from gap to the end, each element compare with data before gap stepsfor(int i = gap; i < length; i++){// element cycle compare with data before gap steps, until 0 indexfor(int j = i; j >= gap; j -= gap){if(array[j] < array[j - gap]){int tmp = array[j];array[j] = array[j - gap];array[j - gap] = tmp;}}}// reduce the stepgap = ceil(gap / 2);}
}void traverse(int *array, int length) // show element one by one
{printf("elements(%d): ", length);for(int k = 0; k < length; k++){printf("%d ", array[k]);}printf("\n");
}编译链接: gcc -o shellsort shellsort.c
执行可执行文件: ./shellsort

相关文章:

【算法】(C语言):快速排序(递归)、归并排序(递归)、希尔排序
快速排序(递归) 左指针指向第一个数据,右指针指向最后一个数据。取第一个数据作为中间值。右指针指向的数据 循环与中间值比对,若大于中间值,右指针往左移动一位,若小于中间值,右指针停住。右…...

模型驱动开发(Model-Driven Development,MDD):提高软件开发效率与一致性的利器
目录 前言1. 模型驱动开发的原理1.1 什么是模型驱动开发1.2 MDD的核心思想 2. 模型驱动开发的优势2.1 提高开发效率2.2 确保代码一致性2.3 促进沟通和协作2.4 方便维护和扩展 3. 实现模型驱动开发的方法3.1 选择合适的建模工具3.1.1 UML3.1.2 BPMN3.1.3 SysML 3.2 建模方法3.2.…...

记录discuz修改用户的主题出售价格
大家好,我是网创有方的站长,今天遇到了需要修改discuz的主题出售价格。特此记录下 方法很简单: 进入用于组-》选择论坛-》批量修改...
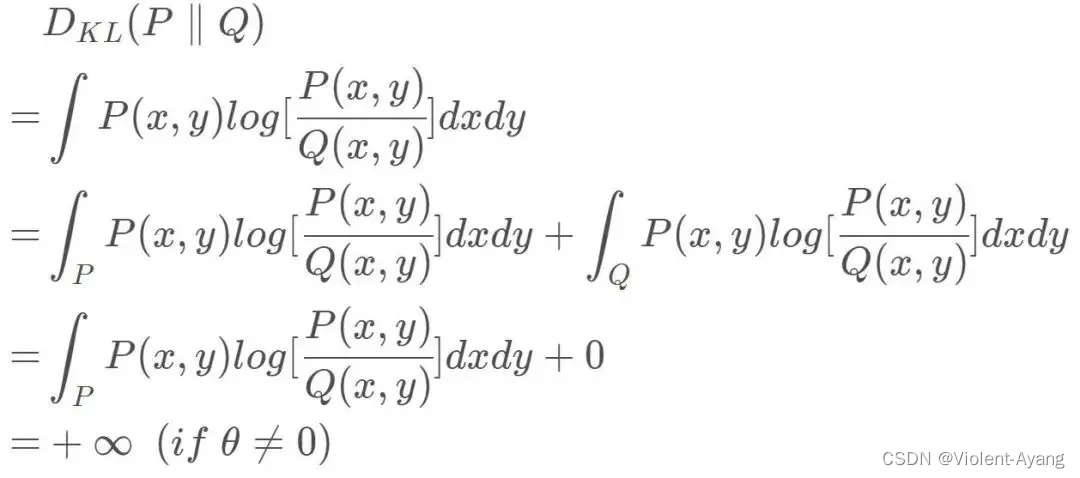
WGAN(Wassertein GAN)
WGAN E x ∼ P g [ log ( 1 − D ( x ) ) ] E x ∼ P g [ − log D ( x ) ] \begin{aligned} & \mathbb{E}_{x \sim P_g}[\log (1-D(x))] \\ & \mathbb{E}_{x \sim P_g}[-\log D(x)] \end{aligned} Ex∼Pg[log(1−D(x))]Ex∼Pg[−logD(x)] 原始 GAN …...
Maven基本使用
1. Maven前瞻 Maven官网:https://maven.apache.org/ Maven镜像:https://mvnrepository.com 1.1、Maven是什么 Maven是一个功能强大的项目管理和构建工具,可以帮助开发人员简化Java项目的构建过程。 在Maven中,使用一个名为 pom.…...

在Linux系统中配置GitHub的SSH公钥
在Linux系统中配置GitHub的SSH公钥,可以让您无需频繁输入密码即可与GitHub仓库进行交互,提高工作效率。以下是配置步骤: 第一步: 检查SSH密钥是否存在 首先,检查您的用户目录下的.ssh文件夹中是否已有SSH密钥。打开终端࿰…...

小酌消烦暑|人间正清欢
小暑是二十四节气之第十一个节气。暑,是炎热的意思,小暑为小热,还不十分热。小暑虽不是一年中最炎热的时节,但紧接着就是一年中最热的节气大暑,民间有"小暑大暑,上蒸下煮"之说。中国多地自小暑起…...

C语言结构体的相关知识
前言 从0开始记录我的学习历程,我会尽我所能,写出最最大白话的文章,希望能够帮到你,谢谢。 1.结构体类型的概念及定义 1.1、概念: 结构体是一种构造类型的数据结构, 是一种或多种基本类型或构造类型的数…...
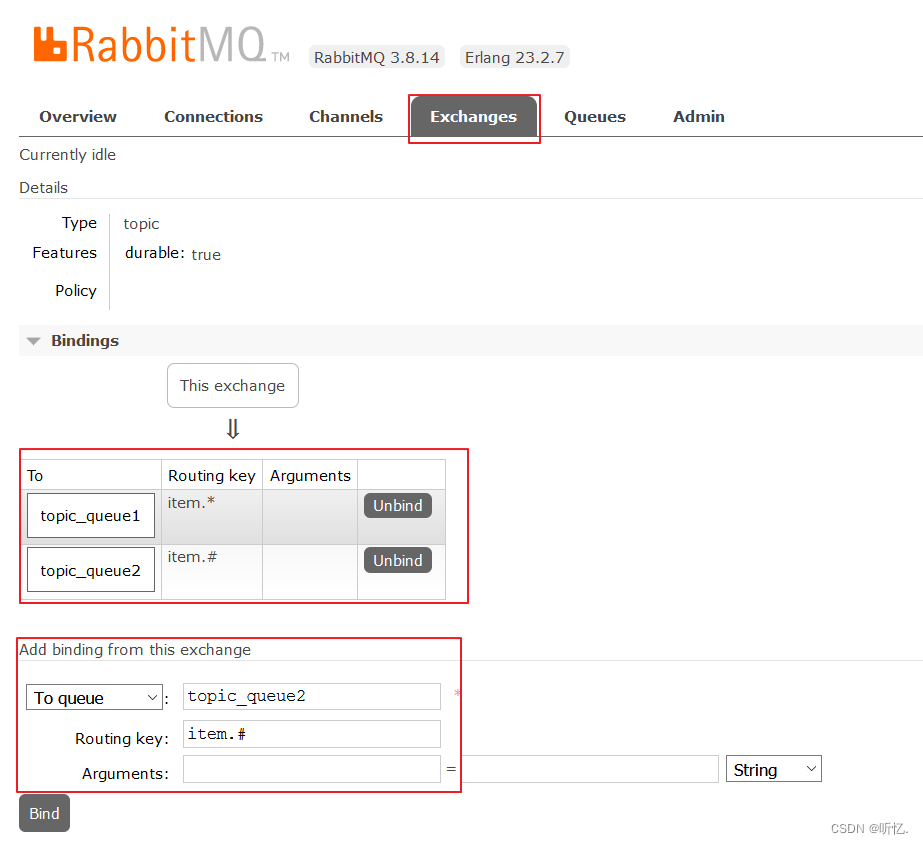
RabbitMQ入门教程(精细版二带图)
目录 六 RabbitMQ工作模式 6.1Hello World简单模式 6.1.1 什么是简单模式 6.1.2 RabbitMQ管理界面操作 6.1.3 生产者代码 6.1.4 消费者代码 6.2 Work queues工作队列模式 6.2.1 什么是工作队列模式 6.2.2 RabbitMQ管理界面操作 6.2.3 生产者代码 6.2.4 消费者代码 …...

IO、零拷贝、多路复用、connection、池化
目录 一、IO 模型 二、什么是网络IO 三、什么是零拷贝 四、多路复用 五、java程序、mysql JDBC connection关系 六、connection怎么操作事务 七 、java里面的池化技术 八、线程池7个核心参数 九、线程的状态 一、IO 模型 BIO :同步阻塞io,单线程 内存上下…...

Lua 错误处理
Lua 错误处理 Lua是一种轻量级的编程语言,广泛用于游戏开发、脚本编写和其他应用程序中。在编程过程中,错误处理是一个重要的方面,它可以帮助开发者创建更健壮和可靠的程序。本文将详细介绍Lua中的错误处理机制。 错误类型 在Lua中&#x…...

二刷力扣——单调栈
739. 每日温度 单调栈应该从栈底到栈顶 是递减的。 找下一个更大的 ,用递减单调栈,就可以确定在栈里面的每个比当前元素i小的元素,下一个更大的就是这个i,然后弹出并记录;然后当前元素i入栈,仍然满足递减…...

elementPlus-vue3-ts表格单选和双选实现方式
记录在vue3、ts、element-plus环境下表格单选和多选的实现方式 单选 html部分 <el-table...reftaskTableRefselect"selectClick"... ><el-table-column type"selection" width"50" />... </el-table>ts部分 const taskTabl…...

Linux系统中卸载GitLab
在Linux系统中卸载GitLab,主要可以通过包管理器(如apt、yum、rpm等)来实现,但具体步骤可能会因GitLab的安装方式(如使用包管理器安装、从源代码安装、使用Docker等)和Linux发行版的不同而有所差异。以下是一…...

基于STM32F407ZG的FreeRTOS移植
1.从FreeRTOS官网中下载源码 2、简单分析FreeRTOS源码目录结构 2.1、简单分析FreeRTOS源码根目录 (1)Demo:是官方为一些单片机移植FreeRTOS的例程 (2)License:许可信息 (3)Sourc…...

【IT领域新生必看】Java编程中的神奇对比:深入理解`equals`与`==`的区别
文章目录 引言什么是操作符?基本数据类型的比较示例: 引用类型的比较示例: 什么是equals方法?equals方法的默认实现示例: 重写equals方法示例: equals与的区别比较内容不同示例: 使用场景不同示…...

WEBHTTP
目录 理解HTTP协议请求流程 1 1 Web基础 2 Hosts文件 1 1 2网页与HTML 2 HTML概述 1 1 3静态网页与动态网页 1.2HTTP协议 1 2 1 HTTP协议概述 1 2 2 HTTP方法 HTTP支持几种不同的请求命令,这些命令被称为HTTP方法(HTTP method 表1一3 HTTP方法 表1&#…...

nodejs 获取客服端ip,以及获取ip一直都是127.0.0.1的问题
一、问题描述 在做登录日志的时候想要获取客户端的ip, 网上查了一下 通过 req.headers[x-forwarded-for] || req.connection.remoteAddress; 获取, 结果获取了之后不管是开发环境,还是生产环境获取到的一直都是 127.0.0.1,这是因为在配置N…...

微软与OpenAI/谷歌与三星的AI交易受欧盟重点关注
近日,欧盟委员会主管竞争事务的副主席玛格丽特维斯塔格(Margrethe Vestager)在一次演讲中透露,欧盟反垄断监管机构将就微软与OpenAI的合作,以及谷歌与三星达成的AI协议寻求更多第三方意见。这意味着微软与 OpenAI、谷歌与三星的 AI 交易及合作…...

微信小程序毕业设计-学生实习与就业管理系统项目开发实战(附源码+论文)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

