绿色金融相关数据合集(2007-2024年 具体看数据类型)
数据类型:
1.绿色债券数据:2014-2023
2.绿色信贷相关数据:2007-2022
3.全国各省及地级市绿色金融指数:1990-2022
4.碳排放权交易明细数据:2013-2024
5.绿色金融试点DID数据:2010-2023
数据来源:
1. 绿色债券数据:本数据来源于Wind数据库和第三方数据库;
2. 绿色信贷相关数据:本数据来源于上市商业银行的年报;
3. 全国各省及地级市绿色金融指数:本数据来源于国家统计局、各省市统计NJ、环境状况公报、《中国科技统计NJ》、《中国金融NJ》、《中国工业统计NJ》、《中国能源统计NJ》等专业统计NJ、中国人民银行等权威机构网站、各上市公司官网、年报等;
4. 碳排放权交易明细数据:本数据来源于各碳排放交易所;
5. 绿色金融试点DID数据:本数据来源于GW院发布文件。
数据范围:
1.绿色债券数据:企业层面
2.绿色信贷相关数据:上市商业银行层面
3.全国各省及地级市绿色金融指数:省份及地级市层面
4.碳排放权交易明细数据:各交易所城市层面
5.绿色金融试点DID数据:地级市层面
样例数据及包含内容:
1.2014-2023年的绿色债券数据,具体展示如下:
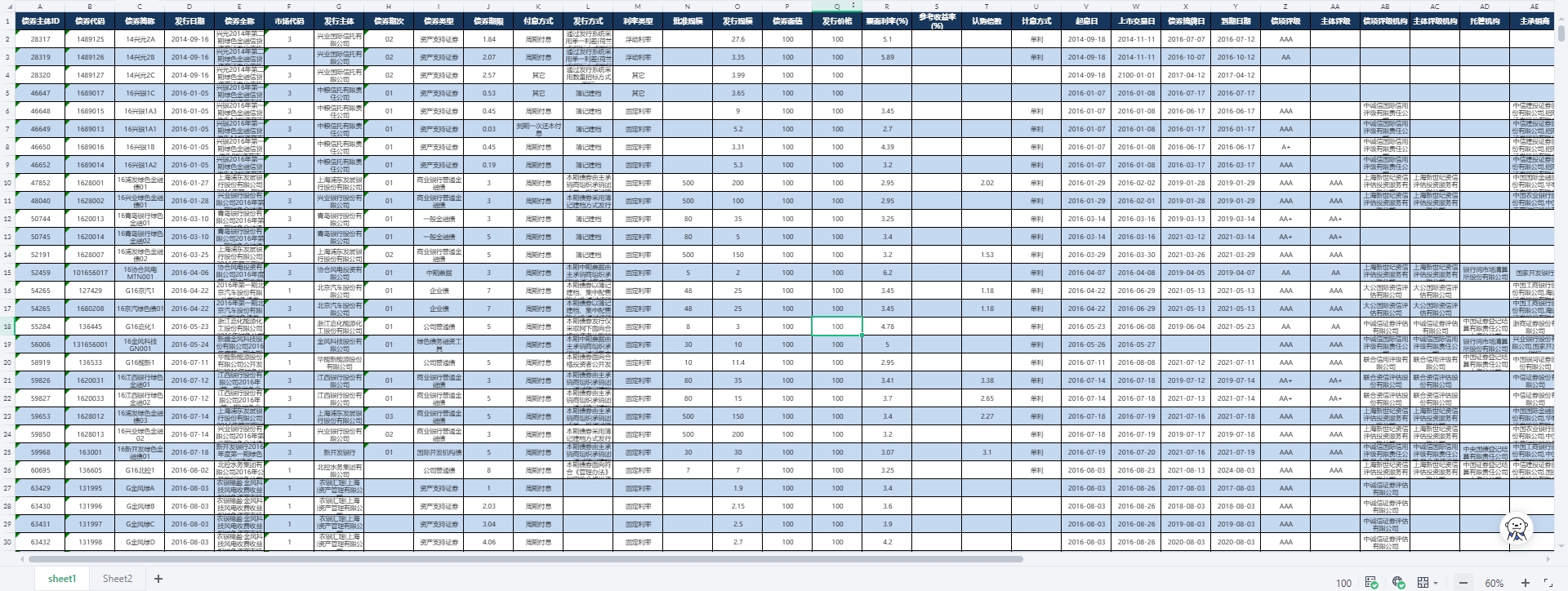

2014-2023年的绿色债券数据下载链接: https://download.csdn.net/download/samLi0620/89519778
2.2007-2022年全国各地区的绿色信贷数据,具体展示如下:
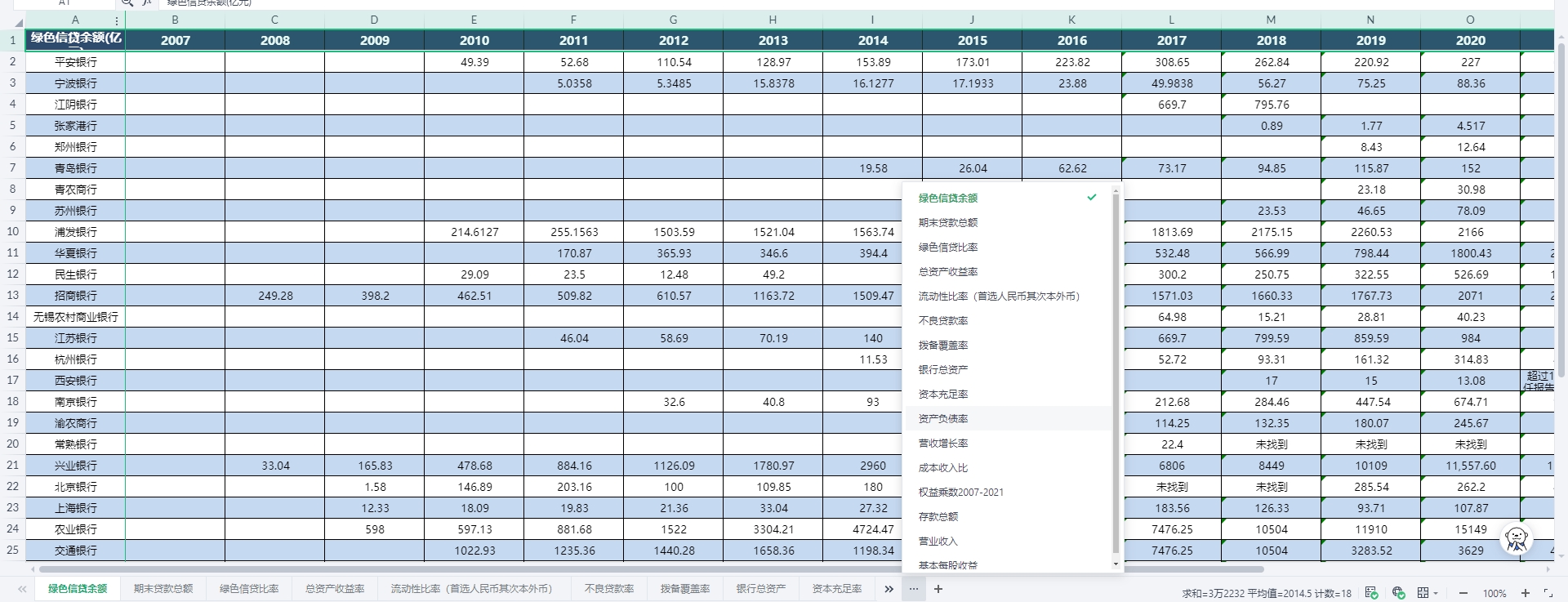

2007-2022年全国各地区的绿色信贷数据下载链接: https://download.csdn.net/download/samLi0620/89519780
3.1990-2022年全国各省及地级市绿色金融指数,具体展示如下:

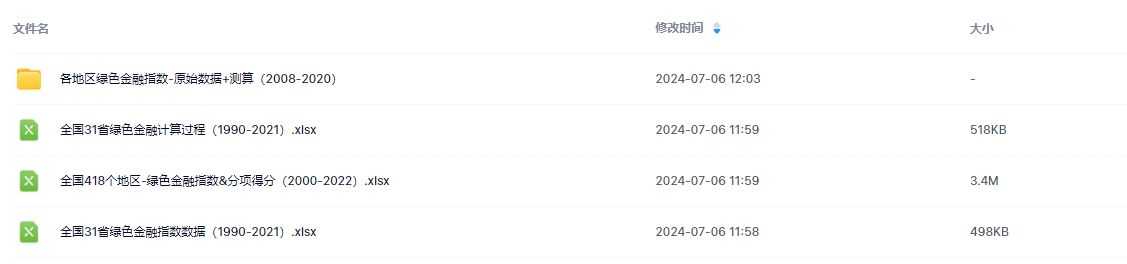
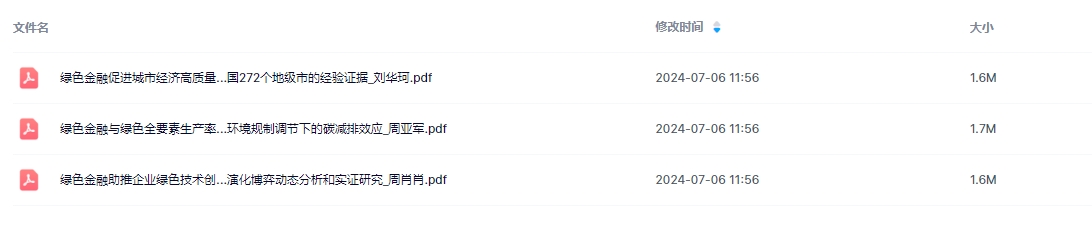
1990-2022年全国各省及地级市绿色金融指数下载链接: https://download.csdn.net/download/samLi0620/89519781
4.2013-2024年碳排放权交易明细数据,具体展示如下:

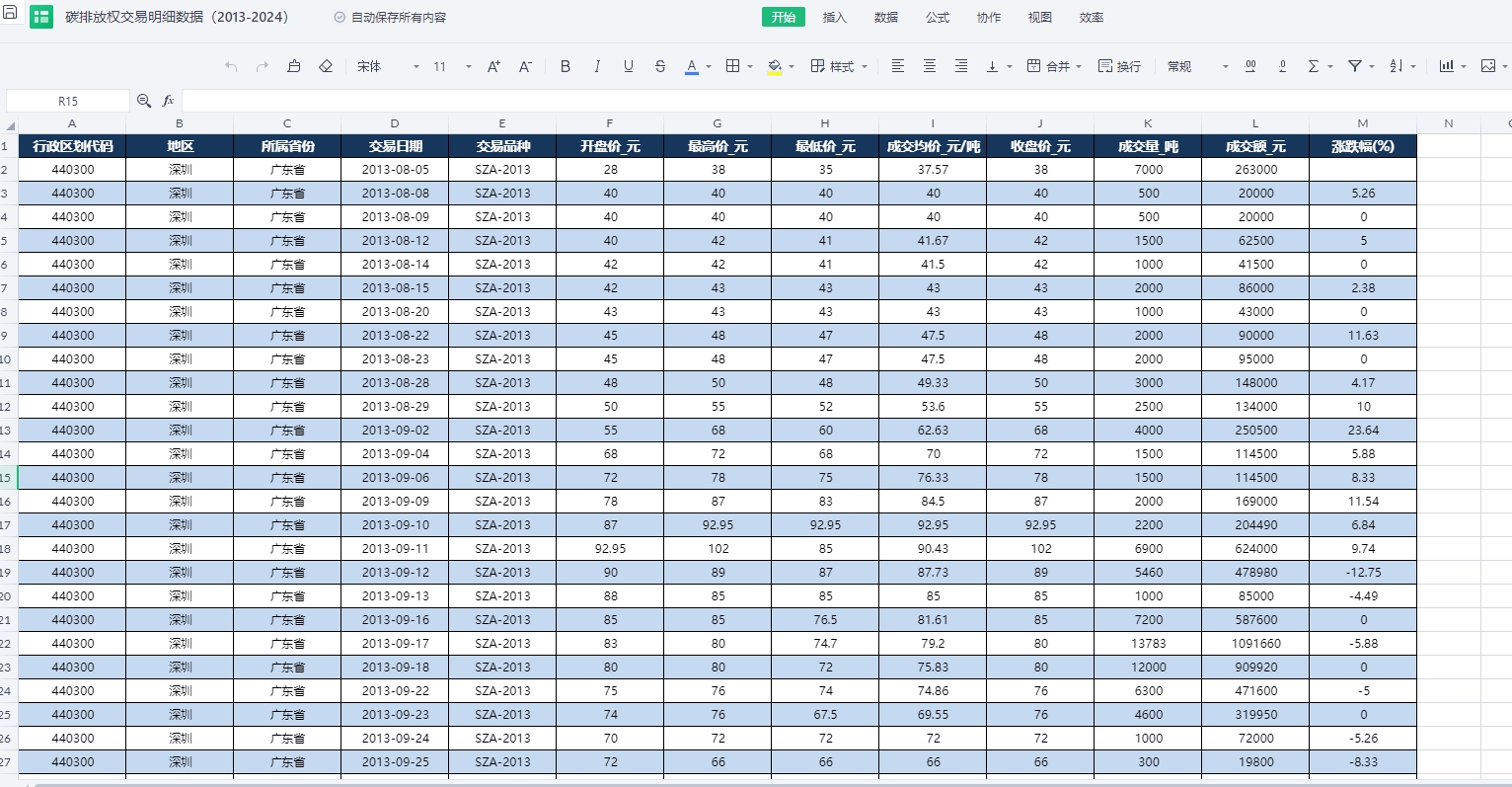
2013-2024年碳排放权交易明细数据下载链接: https://download.csdn.net/download/samLi0620/89519779
5.2010-2023年绿色金融试点DID数据,具体展示如下:

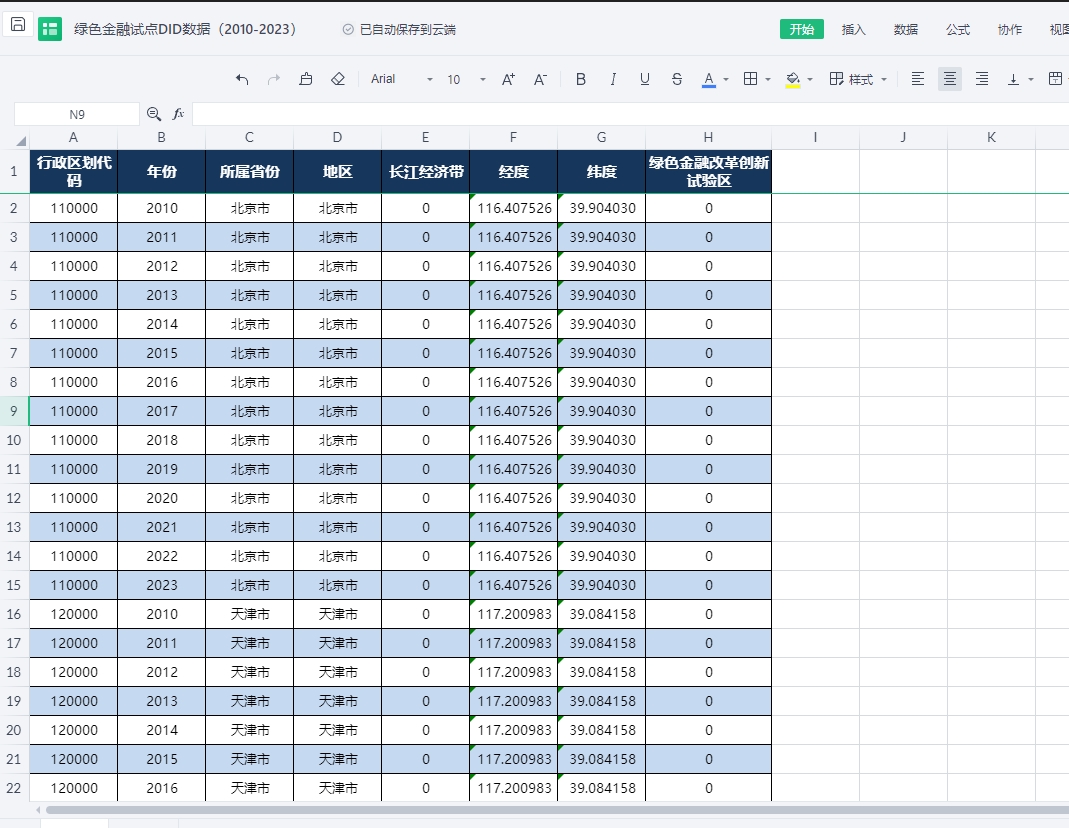
2010-2023年绿色金融试点DID数据下载链接: https://download.csdn.net/download/samLi0620/89519777
参考文献:
[1]崔惠玉,王宝珠,徐颖.绿色金融创新、金融资源配置与企业污染减排[J].中国工业经济,2023(10):118-136.
[2]吴育辉,田亚男,陈韫妍,徐倩.绿色债券发行的溢出效应、作用机理及绩效研究[J].管理世界,2022,38(06):176-193.
[3]周亚军,陈丰泽.绿色金融与绿色全要素生产率:环境规制调节下的碳减排效应[J].生态经济,2023,39(08):43-51.
[4]周肖肖,贾梦雨,赵鑫.绿色金融助推企业绿色技术创新的演化博弈动态分析和实证研究[J].中国工业经济,2023,(06):43-61.
[5]刘华珂,何春.绿色金融促进城市经济高质量发展的机制与检验——来自中国272个地级市的经验证据[J].投资研究,2021,40(07):37-52.
[6]张楠.中国碳排放权交易市场运行状况及其效率分析——基于碳交易价格的测算[J].工业技术经济,2023,42(04):100-107.
相关文章:

绿色金融相关数据合集(2007-2024年 具体看数据类型)
数据类型: 1.绿色债券数据:2014-2023 2.绿色信贷相关数据:2007-2022 3.全国各省及地级市绿色金融指数:1990-2022 4.碳排放权交易明细数据:2013-2024 5.绿色金融试点DID数据:2010-2023 数据来源&#…...

【matlab 项目工期优化】基于NSGA2/3的项目工期多目标优化(时间-成本-质量-安全)
一 背景介绍 本文分享了一个通用的项目工期优化的案例,决策变量是每个子项目的工期,优化目标是项目的完成时间最小,项目的总成本现值最小,项目的总安全水平最高,项目的总质量水平最高。采用的算法是NSGA2和NSGA3算法。…...

Python考前复习
选择题易错: python3不能完全兼容python2内置函数是python的内置对象之一,无需导入其他模块python中汉字变量合法,如“小李123”合法;但T-C不合法,因为有“-”集合无顺序,不能索引;range(5)[2]…...

虚拟机交叉编译基于ARM平台的opencv(ffmpeg/x264)
背景: 由于手上有一块rk3568的开发板,需要运行yolov5跑深度学习模型,但是原有的opencv不能对x264格式的视频进行解码,这里就需要将ffmpegx264编译进opencv。 但是开发板算力有限,所以这里采用在windows下,安…...

react之错误边界
错误边界实质是指什么 实际上是组件 错误边界捕获什么时候的错误 在渲染阶段的错误 错误边界捕获的是谁的错误 捕获的是子组件的错误 错误边界不能捕获什么错误 1、不能捕获异步代码 2、不能捕获事件处理函数 3、不能捕获服务端渲染 4、不能捕获自身抛出的错误 错误…...

openEuler系统之使用Keepalived+Nginx部署高可用Web集群
Linux系统之使用Keepalived+Nginx部署高可用Web集群 一、本次实践介绍1.1 本次实践简介1.2 本次实践环境规划二、keepalived介绍2.1 keepalived简介2.2 keepalived主要特点和功能2.3 使用场景三、Keepalived和Nginx介绍3.1 Nginx简介3.2 Nginx特点四、master节点安装nginx4.1 安…...

基于图像处理的滑块验证码匹配技术
滑块验证码是一种常见的验证码形式,通过拖动滑块与背景图像中的缺口进行匹配,验证用户是否为真人。本文将详细介绍基于图像处理的滑块验证码匹配技术,并提供优化代码以提高滑块位置偏移量的准确度,尤其是在背景图滑块阴影较浅的情…...

【JavaEE精炼宝库】文件操作(1)——基本知识 | 操作文件——打开实用性编程的大门
目录 一、文件的基本知识1.1 文件的基本概念:1.2 树型结构组织和目录:1.3 文件路径(Path):1.4 二进制文件 VS 文本文件:1.5 其它: 二、Java 操作文件2.1 方法说明:2.2 使用演示&…...

常用排序算法_06_归并排序
1、基本思想 归并排序采用分治法 (Divide and Conquer) 的一个非常典型的应。归并排序的思想就是先递归分解数组,再合并数组。归并排序是一种稳定的排序方法。 将数组分解最小之后(数组中只有一个元素,数组有序);然后…...
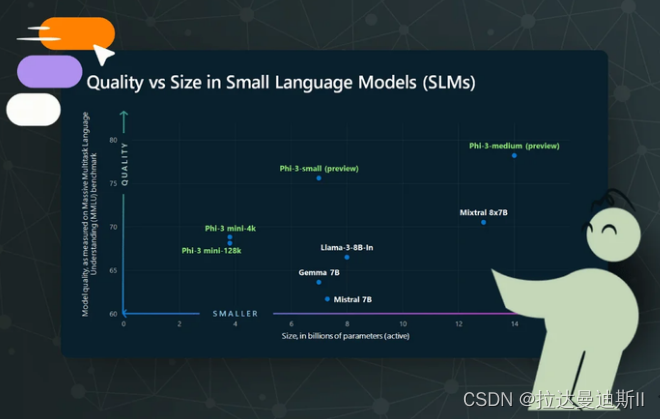
14-8 小型语言模型的兴起
过去几年,我们看到人工智能能力呈爆炸式增长,其中很大一部分是由大型语言模型 (LLM) 的进步推动的。GPT-3 等模型包含 1750 亿个参数,已经展示了生成类似人类的文本、回答问题、总结文档等能力。然而,虽然 LLM 的能力令人印象深刻…...

【Linux】:进程创建与终止
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux程序地址空间的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从…...

横截面交易策略:概念与示例
数量技术宅团队在CSDN学院推出了量化投资系列课程 欢迎有兴趣系统学习量化投资的同学,点击下方链接报名: 量化投资速成营(入门课程) Python股票量化投资 Python期货量化投资 Python数字货币量化投资 C语言CTP期货交易系统开…...

4.2 投影
一、投影和投影矩阵 我们以下面两个问题开始,问题一是为了展示投影是很容易视觉化的,问题二是关于 “投影矩阵”(projection matrices)—— 对称矩阵且 P 2 P P^2P P2P。 b \boldsymbol b b 的投影是 P b P\boldsymbol b Pb。…...

23种设计模式之装饰者模式
深入理解装饰者模式 一、装饰者模式简介1.1 定义1.2 模式类型1.3 主要作用1.4 优点1.5 缺点 二、模式动机三、模式结构四、 装饰者模式的实现4.1 组件接口4.2 具体组件4.3 装饰者抽象类4.4 具体装饰者4.5 使用装饰者模式4.6 输出结果: 五、 应用场景5.1 图形用户界面…...

数据结构--单链表实现
欢迎光顾我的homepage 前言 链表和顺序表都是线性表的一种,但是顺序表在物理结构和逻辑结构上都是连续的,但链表在逻辑结构上是连续的,而在物理结构上不一定连续;来看以下图片来认识链表与顺序表的差别 这里以动态顺序表…...

2024攻防演练:亚信安全推出MSS/SaaS短期定制服务
随着2024年攻防演练周期延长的消息不断传出,各参与方将面临前所未有的挑战。面对强大的攻击队伍和日益严格的监管压力,防守单位必须提前进行全面而周密的准备和部署。为应对这一形势,亚信安全特别推出了为期三个月的MSS/SaaS短期订阅方案。该…...

基于java+springboot+vue实现的在线课程管理系统(文末源码+Lw)236
摘要 本文首先介绍了在线课程管理系统的现状及开发背景,然后论述了系统的设计目标、系统需求、总体设计方案以及系统的详细设计和实现,最后对在线课程管理系统进行了系统检测并提出了还需要改进的问题。本系统能够实现教师管理,科目管理&…...

每日一更 EFK日志分析系统
需要docker和docker-compose环境 下面时docker-compose.yaml文件 [rootnode1 docker-EFK]# cat docker-compose.yaml version: 3.3services:elasticsearch:image: "docker.elastic.co/elasticsearch/elasticsearch:7.17.5"container_name: elasticsearchrestart: …...

python类继承和类变量
Python一些类继承和实例变量的使用 定义基类 class APIException:code 500msg "Sorry, error"error_code 999def __init__(self, msgNone):print("APIException init ...")def error_400(self):pass复用基类的属性值 class ClientTypeError(APIExcept…...

js 随机生成整数
随机生成一个唯一的整数 id export const randomId () > { return Date.now() Math.floor(Math.random() * 10000) } 生成随机ID的方法 // 随机生成0 - 9999 export const randomId ()> { return Math.floor(Math.random() * 10000).toString() } // 随机生成0-999之…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...

Linux信号保存与处理机制详解
Linux信号的保存与处理涉及多个关键机制,以下是详细的总结: 1. 信号的保存 进程描述符(task_struct):每个进程的PCB中包含信号相关信息。 pending信号集:记录已到达但未处理的信号(未决信号&a…...
