集成学习(一)Bagging
前边学习了:十大集成学习模型(简单版)-CSDN博客
Bagging又称为“装袋法”,它是所有集成学习方法当中最为著名、最为简单、也最为有效的操作之一。
在Bagging集成当中,我们并行建立多个弱评估器(通常是决策树,也可以是其他非线性算法),并综合多个弱评估器的结果进行输出。当集成算法目标是回归任务时,集成算法的输出结果是弱评估器输出的结果的平均值,当集成算法的目标是分类任务时,集成算法的输出结果是弱评估器输出的结果少数服从多数。
由于bagging就是将多个模型进行集成,比较简单,所以,本文不讲bagging的原理,通过几个问题让大家彻底了解bagging方法:
一、为什么Bagging算法的效果比单个评估器更好?
二、为什么Bagging可以降低方差?
三、为什么误差可以分解为偏差、方差和噪声?三者分别是什么意思?
四、Bagging有效的基本条件有哪些?Bagging的效果总是强于弱评估器吗?
五、Bagging方法可以集成决策树之外的算法吗?
六、怎样增强Bagging中弱评估器的独立性?
七、除了随机森林,你还知道其他Bagging算法吗?
八、即使是单颗树,为什么它的feature_importances_也会有一定的随机性?
一、为什么Bagging算法的效果比单个评估器更好?
该问题其实是在考察Bagging方法降低模型泛化误差的基本原理。
泛化误差是模型在未知数据集上的误差,更低的泛化误差是所有机器学习/深度学习建模的根本目标。在机器学习当中,泛化误差一般被认为由偏差、方差和噪音构成。
其中偏差是预测值与真实值之间的差异,衡量模型的精度。方差是模型在不同数据集上输出的结果的方差,衡量模型稳定性。噪音是数据收集过程当中不可避免的、与数据真实分布无关的信息。
当算法是回归算法、且模型衡量指标是MSE时,模型的泛化误差可以有如下定义:
泛化误差=偏差*偏差+方差+噪音*噪音 = bias*bias+variance+noise*noise
(该公式可以通过泛化误差、偏差、方差与噪音的定义推导而得,下面有推导)
Bagging的基本思想是借助弱评估器之间的”独立性”来降低方差,从而降低整体的泛化误差。这个思想可以被推广到任意并行使用弱分类器的算法或融合方式上,极大程度地左右了并行融合方式的实际使用结果。其中,“降低方差”指的是bagging算法输出结果的方差一定小于弱评估器输出结果的方差,因此在相同数据上,随机森林往往比单棵决策树更加稳定,也因此随机森林的泛化能力往往比单棵决策树更强。
二、为什么Bagging可以降低方差?
设真实值为,加上误差之后的值为
,模型预测值为 f(x) ,并且误差服从均值为0的正态分布,即
。
偏差:度量了学习算法的期望预期与真实结果的偏离程度,即刻画了学习算法本身的拟合能力,即。
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响,即。
噪声:表达了在当前任务上任何学习算法所能够达到的期望泛化误差的下界,即刻画了学习问题本身的难度,也即。
推导

因此,误差可以分解为偏差、方差与噪声之和。
三、为什么误差可以分解为偏差、方差和噪声?三者分别是什么意思?
3.1 回归问题
以随机森林为例,假设现在随机森林中含有 n 个弱评估器( n 棵树),任意弱评估器上的输出结果是 ,则所有这些弱评估器输出结果的方差可以被表示为
。假设现在我们执行回归任务,则森林的输出结果等于森林中所有树输出结果的平均值,因此森林的输出可以被表示为
,因此随机森林输出结果的方差可以被表示为
,也可以写作
。
当森林中的树互相独立时, 永远小于
,推导如下:

更一般的式子:
![]()
其中, ρ 为弱评估器之间的相关系数,可见当弱评估器之间完全独立时, ρ 为0。与独立时是一样的。这也意味着随机森林输出结果的方差与森林中弱评估器之间的相关性是正相关的。评估器之间的相关性越强,随机森林输出的结果的方差就越大,Bagging方法通过降低方差而获得的泛化能力就越小。
因此,
1、在bagging的弱分类器选取原则中有一条要求弱分类器之间尽可能相互独立,而且独立性越高bagging越有效,当弱评估器之间没有任何独立性了,也即每个弱评估器完全一样,那bagging也就没有任何意义了。
2、同时还要要求弱评估器的方差要大,偏差要小,主要是因为bagging是降低方差,不能够降低偏差,采用大偏差的弱评估器,训练结果非常不可控。
3.2 分类问题
在bagging中,需要对每棵树上的输出结果进行少数服从多数的计算,并将“多数”指向的类别作为随机森林分类器的结果。因此,当弱评估器的方差是 时,随机森林分类器的方差可以写作
,其中
就是sigmoid函数,
是所有弱评估器的分类结果的均值。让
在
处进行一阶泰勒展开,推导如下:

由于为sigmoid函数,所以
,因此有
。
四、Bagging有效的基本条件有哪些?Bagging的效果总是强于弱评估器吗?
(这块要重点记一下)
1、弱评估器的偏差较低,特别地来说,弱分类器的准确率至少要达到50%以上2、弱评估器之间相关性弱,最好相互独立
3、弱评估器是方差较高、不稳定的评估器
1、弱评估器的偏差较低,特别地来说,弱分类器的准确率至少要达到50%以上
Bagging集成算法是对基评估器的预测结果进行平均或用多数表决原则来决定集成评估器的结果。在分类的例子中,假设我们建立了25棵树,对任何一个样本而言,平均或多数表决原则下,当且仅当有13棵以上的树判断错误的时候,随机森林才会判断错误。假设单独一棵决策树在样本上的分类准确率在0.8上下浮动,那一棵树判断错误的概率大约就有
,那随机森林判断错误的概率(有13棵及以上的树都判断错误的概率)是:
![]()
可见,判断错误的几率非常小,这让随机森林的表现比单棵决策树好很多。基于上述式子,我们可以绘制出以弱分类器的误差率为横坐标、随机森林的误差率为纵坐标的图像。

可以从图像上看出,当基分类器的误差率小于0.5,即准确率大于0.5时,集成的效果是比弱分类器要好的。相反,当基分类器的误差率大于0.5,袋装的集成算法就失效了。所以在使用随机森林之前,一定要检查,用来组成随机森林的分类树们是否都有至少50%的预测正确率。
2、弱评估器之间相关性弱,最好相互独立
在证明Bagging降低方差的数学过程中已经申明了很多次,唯有弱评估器之间相互独立、弱评估器输出的结果相互独立时,方差计算公式的前提假设才能被满足,Bagging才能享受降低方差的福利。
然而在现实中,森林中的弱评估器很难完全相互独立,因为所有弱评估器都是在相同的数据上进行训练的、因此构建出的树结构也大同小异。幸运的是,我们能够衡量弱评估器之间相关性。以随机森林回归为例,假设任意弱评估器之间的相关系数为 ρ ,则随机森林输出结果的方差等于:
![]()
这个公式是根据比奈梅定义(Bienaymé's Identity)与协方差相关的公式推导出来的,这暗示随机森林输出结果的方差与森林中弱评估器之间的相关性是正相关的,弱评估器之间的相关性越强,随机森林输出的结果的方差就越大,Bagging方法通过降低方差而获得的泛化能力就越小。因此在使用随机森林时,我们需要让弱评估器之间尽量相互独立,我们也可以通过这一点来提升随机森林的水平。
3、弱评估器是方差较高、不稳定的评估器
因为Bagging是作用于方差的集成手段,所以Bagging方法擅长处理方差大、偏差低的模型,而不擅长处理方差小、偏差大的模型,对于任意算法而言,方差与偏差往往不可兼得,这也很容易理解——想要在当前数据集上获得低偏差,必然意味着需要重点学习当前数据集上的规律,就不可避免地会忽略未知数据集上的规律,因此在不同数据集上进行测试时,模型结果的方差往往很大。
五、Bagging方法可以集成决策树之外的算法吗?
强大又复杂的算法如决策树、支持向量机等,往往学习能力较强,倾向于表现为偏差低、方差高,这些算法就比较适合于Bagging。而线性回归、逻辑回归、KNN等复杂度较低的算法,学习能力较弱但表现稳定,因此倾向于表现为偏差高,方差低,就不太适合被用于Bagging。
六、怎样增强Bagging中弱评估器的独立性?
正如前述,在实际使用数据进行训练时,我们很难让Bagging中的弱评估器完全相互独立,主要是因为:
(1)训练的数据一致
(2)弱评估器构建的规则一致
导致最终建立的弱评估器都大同小异,Bagging的效力无法完整发挥出来。为了弱评估器构建规则一致的问题,有了Averaging和Voting这样的模型融合方法:基本来看,就是使用Bagging的逻辑来融合数个不同算法的结果。而当我们不使用模型融合时,我们可以使用“随机性”来削弱弱分类器之间的联系、增强独立性、提升随机森林的效果。
在随机森林中,天生就存在有放回随机抽取样本建树的机制,因此才会有bootstrap、max_samples等参数,才会有袋外数据、袋外评估指标oob_score等属性,意在使用不同的数据建立弱评估器。除了有放回随机抽样之外,还可以使用max_features随机抽样特征进行分枝,加大弱评估器之间的区别。
正因为存在不同的随机的方式,Bagging集成方法下才有了多种不同的算法。
七、除了随机森林,你还知道其他Bagging算法吗?
Bagging方法的原理简单,因此Bagging算法之间的不同主要体现在随机性的不同上。在上世纪90年代,对样本抽样的bagging、对特征抽样的bagging、对样本和特征都抽样的bagging都有不同的名字,不过今天,所有这些算法都被认为是装袋法或装袋法的延展。在sklearn当中,除了随机森林之外还提供另一个bagging算法:极端随机树。极端随机树是一种比随机森林更随机、对方差降低更多的算法,我们可以通过以下两个类来实现它:
- sklearn.ensemble.ExtraTreesClassifier
- sklearn.ensemble.ExtraTreesRegressor
与随机森林一样,极端随机树在建树时会随机挑选特征,但不同的是,随机森林会将随机挑选出的特征上每个节点都进行完整、精致的不纯度计算,然后挑选出最优节点,而极端随机树则会随机选择数个节点进行不纯度计算,然后选出这些节点中不纯度下降最多的节点。这样生长出的树比随机森林中的树更不容易过拟合,同时独立性更强,因此极端随机树可以更大程度地降低方差。
当然了,这种手段往往也会带来偏差的急剧下降,因此极端随机树是只适用于方差过大、非常不稳定的数据的。除非特殊情况,我们不会考虑使用极端随机树。
八、即使是单颗树,为什么它的feature_importances_也会有一定的随机性?
这种随机性源于CART树对切分点的选取。根据评估器的说明,哪怕是max_features=n_features(即每次训练带入全部特征、而max_features<n_features时则每次切分带入部分特征、此时随机性更强),在进行决策树生长时也经常遇到拥有相同效力的备选切分点(即基于基尼系数的信息增益相同),此时只能随机挑选其中一个备选点进行切分,而选取哪个切分点,就必然给对应的特征累计更多的重要性。这也就是为何相同的数据在多次建模时特征重要性会各不相同的原因。
记下来学习:集成学习(二)Boosting-CSDN博客
相关文章:

集成学习(一)Bagging
前边学习了:十大集成学习模型(简单版)-CSDN博客 Bagging又称为“装袋法”,它是所有集成学习方法当中最为著名、最为简单、也最为有效的操作之一。 在Bagging集成当中,我们并行建立多个弱评估器(通常是决策…...

Docker 中查看及修改 Redis 容器密码的实用指南
在使用 Docker 部署 Redis 容器时,有时我们需要查看或修改 Redis 的密码。本文将详细介绍如何在 Docker 中查看和修改 Redis 容器的密码,帮助你更好地管理和维护你的 Redis 实例。 一、查看 Redis 容器密码 通常在启动 Redis 容器时,我们会…...

CH09_JS的循环控制语句
第9章:Javascript循环控制语句 本章目标 掌握break关键字的使用掌握continue关键字的使用 课程回顾 for循环的特点和语法while循环的特点和语法do-while循环的特点和语法三个循环的区别 讲解内容 1. break关键字 为什么要使用break关键字 生活中,描…...

Python实现Mybatis Plus
Python实现Mybatis Plus from flask import g from sqlalchemy import asc, descclass QueryWrapperBuilder:conditions {}order_by_info {}def __new__(cls, *args, **kwargs):obj super(QueryWrapperBuilder, cls).__new__(cls)return objdef __init__(self, obj):self.o…...

卷积神经网络和Vision Transformer的对比之归纳偏置
卷积神经网络(CNN)和视觉变换器(Vision Transformer,ViT)是两种常用于图像处理的深度学习模型。它们各有优缺点,其中一个重要的区别在于它们对图像数据的“归纳偏置”(inductive bias࿰…...

Java之网络面试经典题(一)
目录 编辑 一.Session和cookie Cookie Session 二.HTTP和HTTPS的区别 三.浅谈HTTPS为什么是安全的? 四.TCP和UDP 五.GET和Post的区别 六.forward 和 redirect 的区别? 本专栏全是博主自己收集的面试题,仅可参考,不能相…...

Failed to download metadata for repo ‘docker-ce-stable‘
这个问题是由于在安装 clamav 和 clamav-update 时,无法下载 Docker CE Stable 库的元数据,可能的原因是网络连接超时或访问该网址受限。以下是一些可能的解决办法: 检查网络连接: 确保服务器的网络连接正常,尤其是与互…...

vant拍摄视频上传以及多张图片上传
数据定义 data() {return {fileList: [],vedioList: [],formData: ,fileTypes: image/png,image/jpeg,image/jpg,image/jpeg,} }, beforeMount() {this.formData new FormData() },拍摄视频上传 <van-uploaderv-if"radio 1"v-model"vedioList"accep…...

如何用手机拍出高级感黑白色调照片?华为Pura70系列XMAGE演绎黑白艺术
在影像的世界里,色彩可以让画面更丰富,更具有表现力,往往也能带来更多的视觉冲击。但有时候,黑白却有着一种独特的魅力。华为Pura 70系列XMAGE黑白风格,则给我们了一把通过纯粹艺术大门的钥匙。 XMAGE黑白并非简单的色…...

Cartographer前后端梳理
0. 简介 最近在研究整个SLAM框架的改进处,想着能不能从Cartographer中找到一些亮点可以用于参考。所以这一篇博客希望能够梳理好Cartographer前后端优化,并从中得到一些启发。carto整体是graph-based框架,前端是scan-map匹配,后端…...

Java面试题系列 - 第3天
题目:Java集合框架详解与高效使用策略 背景说明:Java集合框架是Java标准库的重要组成部分,提供了一系列容器类,如List、Set、Map等,用于存储和操作集合数据。熟练掌握集合框架的使用,对于编写高效、健壮的…...

【Spring Boot】Spring Boot简介
1、概述 Spring Boot是一个用于创建独立、生产级别的基于Spring的应用程序的开发框架。旨在简化Spring应用的初始搭建和开发过程。它通过自动配置和大量默认配置,使得开发者能够快速搭建一个独立的Spring应用,无需进行大量的手动配置。 2、主要特点 快…...

Akamai+Noname强强联合 | API安全再加强
最近,Akamai正式完成了对Noname Security的收购。本文我们将向大家介绍,经过本次收购后,Akamai在保护API安全性方面的后续计划和未来愿景。 Noname Security是市场上领先的API安全供应商之一,此次收购将让Akamai能更好地满足日益增…...

第四届BPAA算法大赛成功举办!共研算法未来
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的…...

2024第三届中国医疗机器人大会第一轮通知
2024第三届中国医疗机器人大会第一轮通知 大会背景 医疗机器人技术正以前所未有的速度在主流医学领域取得卓越进展,新应用、新技术不断涌现,使得该领域在过去一年中取得了令人惊叹的增长。然而,这仅仅是冰山一角,未来的发展空间仍…...

常见算法和Lambda
常见算法和Lambda 文章目录 常见算法和Lambda常见算法查找算法基本查找(顺序查找)二分查找/折半查找插值查找斐波那契查找分块查找扩展的分块查找(无规律的数据) 常见排序算法冒泡排序选择排序插入排序快速排序递归快速排序 Array…...

自动缩放 win7 远程桌面
https://mremoteng.org/download 用这个软件,下载 zip 版,不需要管理员权限 在这里找到的,选票最高的一个就是 https://superuser.com/questions/1030041/remote-desktop-zoom-and-full-screen-how-win10-remote-win7-2008-2003-ho...
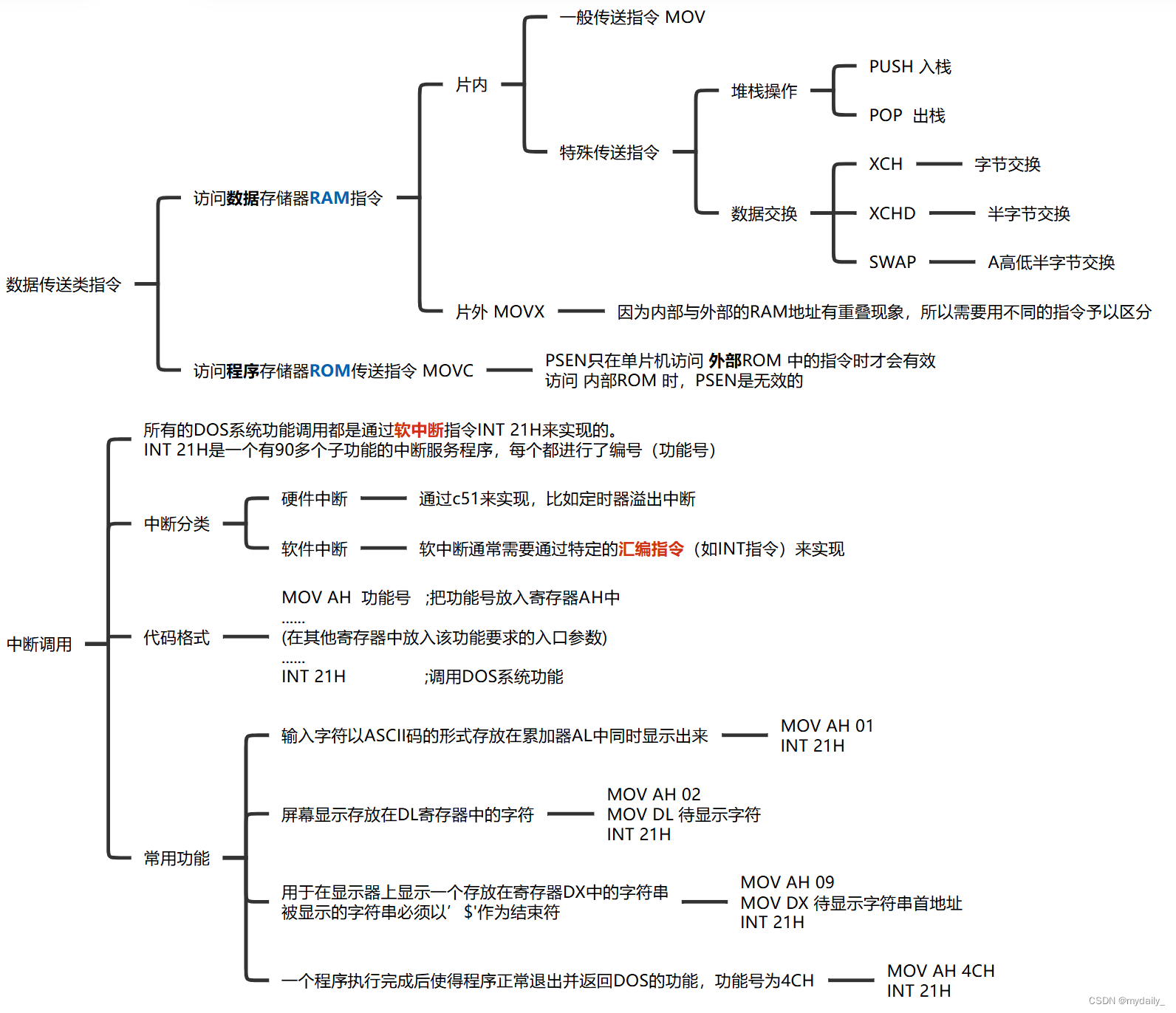
微机原理与单片机 知识体系梳理
单片机笔记分享 我个人感觉单片机要记的东西很多,也很琐碎,特别是一些位、寄存器以及相关作用等,非常难以记忆。因此复习时将知识点整理在了一起做成思维导图,希望对大家有所帮助。内容不是很多,可能有些没覆盖全&…...

低音炮内存卡格式化后无法播放音乐文件
试了多次 不支持ntfs不支持exfat 仅支持fat32 FAT32与exFAT的区别主要体现在来源、单个文件限制、适用情况以及兼容性方面。12 来源: FAT32是Windows平台的传统文件格式,首次在Windows 95第二版中引入,旨在取代FAT16,具有良好的…...

手动将dingtalk-sdk-java jar包打入maven本地仓库
有时候,中央镜像库不一定有自己需要的jar包,这时候我们就需要用到该方法,将jar打入maven本地仓库,然后项目中,正常使用maven的引入规则。 mvn install:install-file -Dmaven.repo.local=D:\software\maven\apache-maven-3.6.3-bin\apache-maven-3.6.3\repo -DgroupId=ding…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
